基于集中-分散交易机制的多产消者两阶段鲁棒优化模型

王善磊，孙国强，吴 晨，，胡国伟，周亦洲，陈 胜，卫志农

（1. 河海大学 能源与电气学院，江苏 南京 211100；2. 国网江苏省电力有限公司经济技术研究院，江苏 南京 210008）

0 引言

随着分布式能源技术的快速发展以及电力体制改革的稳步推进，兼具电能生产与消费能力的产消者在配电网中的数量逐渐增多，并且开始作为新兴的市场主体参与用户侧市场化交易。产消者一般是由用户侧分布式光伏PV（PhotoVoltaic）、电动汽车EV（Electric Vehicle）、中央空调系统CACS（Central Air-Conditioning System）等资源整合而成的聚合体［1］，具有源荷双重属性，其显著特点是电力与信息高度融合交互，且对价值信号高度敏感。

2017 年11 月，国家发展改革委、国家能源局发布了《关于开展分布式发电市场化交易试点的通知》，为用户侧市场化交易的开展提供了政策支撑。然而，以产消者为代表的用户侧独立主体在参与市场交易时不可避免地面临以下问题：受到自身容量限制，产消者单独参与电力现货市场交易缺乏市场竞争力；产消者多位于系统末端，电网对其不可观，因此难以被准确地调控［2］。在此背景下，地域上相邻的各产消者可组成多产消者联盟，通过彼此间及与市场运营商MO（Market Operator）的协调进一步提高自身用电经济性与供电可靠性，实现多种能源的优势互补与梯级利用。

目前，国内外学者在产消者的能量管理与市场化交易方面已取得了较多的研究成果。文献［3-4］采用兼顾控制与经济手段的交互能源机制对大规模产消者群进行优化调度。文献［5］研究在集中交易模式下产消者的需求响应机制，在满足用户舒适度的前提下对建筑能耗进行系统优化。文献［6］提出一种在分时电价TOU（Time Of Use）场景下的产消者日前竞标模型，通过“源-荷-储”的协同调度优化产消者的集中交易电量。文献［7］设计适用于大量产消者参与的合作模型收益分配方案。

然而，文献［3-7］仅考虑产消者与外部电网的单一交互关系，各主体仅与上级MO 存在能量交互，没有很好地利用各主体的互补特性，在整体资源的最优利用方面存在欠缺。实际上，由于多个产消者的用电行为以及用电模式具有良好的互补特性以及交互关系，因此对产消者交易策略的研究不应局限于产消者与上级MO 之间，还应逐渐向产消者之间的协调发展。文献［8］研究社区产消者市场交易策略，基于主从-演化博弈方法确定产消者之间的分散交易电价。文献［9］基于连续双向拍卖机制模拟竞争市场环境下产消者间的分散交易机制。文献［10］设计基于点对点P2P（Peer to Peer）模式的多产消者分散交易机制，通过有限的信息交互实现模型的迭代求解，降低了交易方的信息暴露风险。文献［11-12］研究基于合作博弈的多产消者能量共享策略，并采用Shapley值法对合作剩余进行分配。尽管文献［8-12］考虑了产消者之间的分散交易模式，但是产消者的集中-分散交易策略往往需要在日前作出决定，且这些文献均未考虑PV 等不确定因素对产消者市场交易策略的影响。

因此，本文在上述研究的基础上，进一步采用两阶段鲁棒优化方法处理PV出力的不确定性，建立基于两阶段鲁棒优化的多产消者集中-分散市场交易模型，将该模型转换为电能交易状态组合主问题以及不确定性因素影响下的经济调度子问题，并通过列和约束生成C&CG（Column and Constraint Generation）法交替迭代主问题与子问题，实现模型的高效求解，求解结果能在一定程度上降低产消者交易策略的保守性，提高决策的经济性。此外，为了保证联盟长期稳定，在交易策略确定后，进一步采用Nash谈判法对多个产消者的合作剩余进行统一分配。相较于仅考虑边际贡献度的Shapley值法，Nash谈判法综合考虑了各产消者的风险偏好、边际贡献及供需比等因素，评价指标更全面，分配策略更科学。最后，以包含1 个MO 与3 个产消者的算例验证了所建模型在决策经济性、新能源消纳、调度灵活性方面的优势，并对C&CG算法的性能进行了系统测试。

1 基于集中-分散交易机制的多产消者两阶段鲁棒交易模型

由于多个产消者的用电行为以及用电模式具有良好的互补特性以及交互关系，因此，可将价格作为驱动力对集群化产消者进行资源的有效管理，从而在多时间尺度、多层级上发挥产消者聚合资源的灵活性价值，这种能源交易机制又被称为交互式能源TE（Transactive Energy）机制。目前，已有部分区域的电力系统能源交易与管理初步采用了该方法，如北欧电力市场的日前能源交易［13］。在具体项目方面，美国的Olympic Peninsual 项目、Transactive Grid项目及荷兰的Powermatching City 项目均为比较典型的交互能源项目，目前我国的浙江能源服务商也在积极探索以TE机制推进浙江高弹性电网的建设。

总体而言，现阶段TE 机制主要包括集中式交易模式以及集中-分散混合交易模式［13］。在集中式交易模式下，可供产消者选择的交易策略较为单一，产消者仅能够直接与MO进行交易。而在集中-分散混合交易模式下，各产消者以价格信号作为导向，可以灵活选择与其他产消者或MO进行交易，该模式下产消者的市场交易框架如图1所示。由图可见，产消者内部含有能量管理系统EMS（Energy Management System）等计算资源，其具有人机交流、数据分析、预测以及决策优化等功能，能够及时收集上级MO 发布的电价以及服务费用信息，并结合自身新能源出力预测值确定相应的能量管理策略，提高能量管理水平。通常情况下，多电产消者向MO 售电的电价要低于少电产消者从MO 购电的电价［11］，故同一配电区域的多个产消者可组成合作联盟，通过联盟内部的电能共享，减少整体向MO 的购电量，从而节约用电成本，提高经济效益。

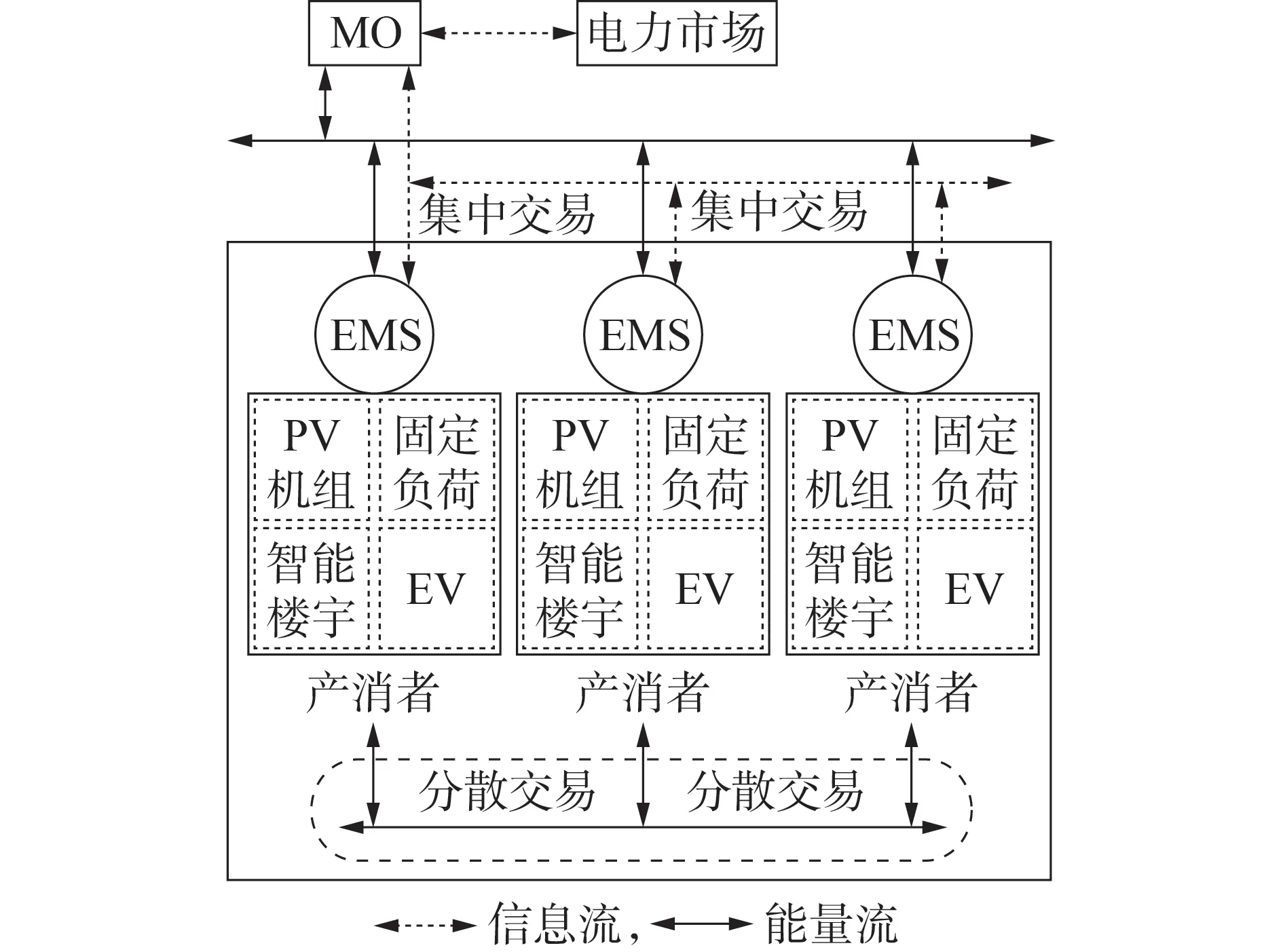
图1 多产消者集中-分散交易框架Fig.1 Centralized-decentralized trading framework of multiple prosumers

集中-分散交易模式下，各产消者的交易顺序如下：各产消者优先与相邻产消者进行交易，使得清洁能源以及多电产消者的电能尽可能地在系统内部消纳，该交易为去中心化的交易，由产消者之间直接P2P 进行交易，交易平台为P2P 交易平台［14］；分散交易完成后，各产消者将富余电量或缺额电量信息上报至MO，MO 确定与各产消者的集中交易电量；集中交易完成后，MO 结合各产消者的基本信息组织Nash 谈判，并发布最终谈判结果以及收益分配系数，对多产消者的合作剩余进行统一分配。

1.1 产消者内部聚合单元建模

由于产消者主要是用户侧可控资源，因此本文考虑的产消者内部聚合单元包括用户侧EV、CACS、PV以及固定负荷，各部分数学模型如下。

1.1.1 EV模型

本文假设各产消者内的EV用车习惯相对固定，设定为在t1时刻并网，在t2时刻离网，其并网时段集合记为Tp，EV 充放电过程中会产生电池折旧费用CEV，表示如下：

1.2 多产消者集中-分散交易建模

1）交易状态约束，即：

4）交易费用计算。多产消者集中-分散交易过程中产生的费用主要包括产消者间的电能交易费用以及产消者与MO的电能交易费用，具体如下。

（1）产消者间的电能交易费用包括买卖双方缴纳给MO 的固定服务费用以及与电量相关的直接购电或售电费用。需要注意的是，由于产消者间的交易电价、总售电量以及总购电量均相同，因此产消者内部所产生的与电量相关的交易费用为0，产消者间的交易费用仅涉及服务费用Cvpa，如式（23）所示。

1.3 计及不确定性的多产消者两阶段鲁棒交易模型

由于PV出力具有较强的随机性，因此产消者在日前交易决策的过程中需要考虑PV 出力波动性的影响，本文以两阶段鲁棒优化方法处理PV出力的不确定性，构建基于两阶段鲁棒优化的多产消者市场交易模型，并利用C&CG 算法将模型转换为交易状态组合主问题以及经济调度子问题进行交替求解。

1.3.1 不确定变量集合的构建

本文将PV出力以不确定集合的形式进行描述。首先，基于历史数据信息预测一定时间内PV出力的标称值；然后，预测随机场景下PV 出力的最大波动范围；最后，将PV 出力的不确定性表示为不确定集合D。具体如下：

针对式（26）所示的两阶段鲁棒交易模型，本文采用C&CG 算法实现该模型的高效求解［17］。模型的详细分解方法以及转换过程见附录A 式（A1）—（A20）所示。基于C&CG 算法的多产消者两阶段鲁棒集中-分散交易模型的求解流程图见附录A图A1。

2 基于Nash谈判的多产消者收益分配

实际上，由于各产消者自身市场力水平存在差异，若产消者间的交易电价过低，则市场力较强的产消者可能会选择退出合作联盟以谋求新的合作对象，因此，为保证联盟的长久稳定，还需要考虑多产消者联盟的合作剩余分配问题。本文以Nash 谈判法作为多产消者合作剩余的分配方法，结合各产消者的风险偏好、边际贡献度以及平均供需比3 个因素，对各产消者的综合谈判力进行量化，并根据各产消者的综合谈判力确定最终的谈判策略，从而实现多产消者合作剩余的公平分配。此外，Nash 谈判法是一种事后分配机制，需要根据产消者两阶段鲁棒交易模型决策结果进行相关谈判指标的计算。

2.1 Nash谈判理论

2.2 Nash均衡点的计算

2.2.1 效用函数的构建

效用函数反映了谈判者对收益的偏好，具有主观和客观双重特性。本文以谈判者对风险的偏好程度来具体刻画效用函数。经标准化处理后，效用函数是定义域和值域均在[0，1]区间上的单调递增函数。在该条件下，按决策者对风险的偏好程度，效用函数可分为以下3种。

1）风险偏好型。风险偏好型谈判者的效用函数表现为随着谈判力的增加，效用值的增长速度也加快，即效用函数的一阶导数应单调递增。本文采用底数为自然对数的指数函数描述该效用函数［19］：

式中：m、n为常系数，由于效益函数总是经过（0，0）和（1，1）这2个特殊点的，因此，依次将这2个特殊点代入效益函数，可分别求解式（28）—（30）各效用函数中m、n具体数值。

2.2.2 初始谈判点

初始谈判点定义为产消者i参与合作联盟期望获得的最小分配系数，表明了参与者的谈判底线。若实际收益分配系数小于该分配系数，则谈判破裂，产消者i退出联盟。初始谈判点的计算如下：

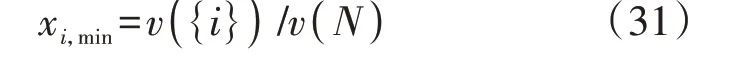
式中：v( · )为特征函数，v({i})为产消者i单独参与交易的特征函数，v(N)为全联盟时的特征函数，具体计算公式见附录B式（B1）、（B2）。

2.2.3 综合谈判力

从Nash 均衡解的形式上可见，谈判力是决定各参与者收益分配系数的重要因素，本文从边际贡献度以及平均供需比2个角度对该指标进行量化。

1）边际贡献度。边际贡献度Smci是收入分配公平性的直接体现，定义如下：

结合目标函数式（27）以及相关约束式（28）—（35），可计算出各产消者的收益分配系数。

3 算例测试与结果分析

3.1 算例描述

本文以包含1 个MO 与3 个产消者的算例验证所建模型以及所提算法的有效性。采用高斯过程预测产消者的PV出力标称值以及波动区间［20］，具体预测结果如附录C 图C1—C3 所示，各产消者的负荷功率曲线如附录C 图C4 所示。结合图C1—C4 可知，各产消者间存在一定的电能互补特性，因此可通过各产消者间以及产消者与MO 的协调进一步提高产消者的用电经济性与供电可靠性，实现多种能源的优势互补与梯级利用。产消者间、产消者与MO间的单次交易电量上限设为50 MW。各产消者内均含有一定数量的EV，其聚合后的等效参数见文献［15］。各产消者内聚合的CACS 型号一致，其基本参数见附录C 表C1。智能楼宇相关热参数取自文献［16］。PV运行维护费用［11］取为0.03元／（kW·h），EV 充放电费用为0.08 元／（kW·h），多产消者间内部交易的服务费用固定为每笔0.2 元，产消者与MO间的固定交易服务费用固定为每笔0.3 元。产消者间、产消者与MO间的交易电价［15］见附录C表C2。根据不同产消者的PV出力波动区间，可将产消者1—3依次划归为风险偏好、风险中立以及风险规避型。

本文采用GAMS 24.4 软件对上述模型进行编程求解。其中：对于多产消者两阶段鲁棒交易模型，采用GAMS软件调用CPLEX求解器对主问题及子问题进行迭代求解；而Nash 谈判过程为非线性模型，采用GAMS软件调用IPOPT求解器对其直接求解。

3.2 算例结果分析

3.2.1 不同交易策略结果分析

为对比不同交易机制下多产消者整体的运行方式以及运行成本，设置以下对比算例：Case 1，产消者间可进行P2P交易，按本文所提出的集中-分散交易机制进行交易策略优化；Case 2，产消者间不进行分散式电量交易，各产消者仅参与集中交易。

以产消者1为例，2种算例下其基本调度策略如附录D 图D1 所示。整体而言，2 种交易模式下产消者1 内部各聚合单元的调度计划基本一致，而EV 的充放电策略有所不同。在Case 1 下，由于产消者可参与分散交易，市场交易策略更灵活，因此其EV 的充放电行为更频繁，充放电策略更灵活。此外，产消者间的分散交易多发生在各产消者负荷相对较低且PV 功率相对较高的07:00—13:00 时段，而在20:00至次日06:00时段，所有产消者均只参与集中交易。

2种算例下产消者与MO 的市场交易电量如图2所示。由图可以看出，在Case 1 下，除了部分时刻产消者购电量略高于Case 2 外，在其余大多数时间内Case 1 下的购电量和售电量均低于Case 2，尤其是在07:00—16:00 时段，Case 1 下的产消者无需向MO购电，仅通过产消者间的分散交易即可满足自身负荷的用电需求，而在Case 2 下少电产消者仍需购电以满足负荷需求。可见，集中-分散交易机制下产消者的市场交易策略更加灵活且更具经济性。

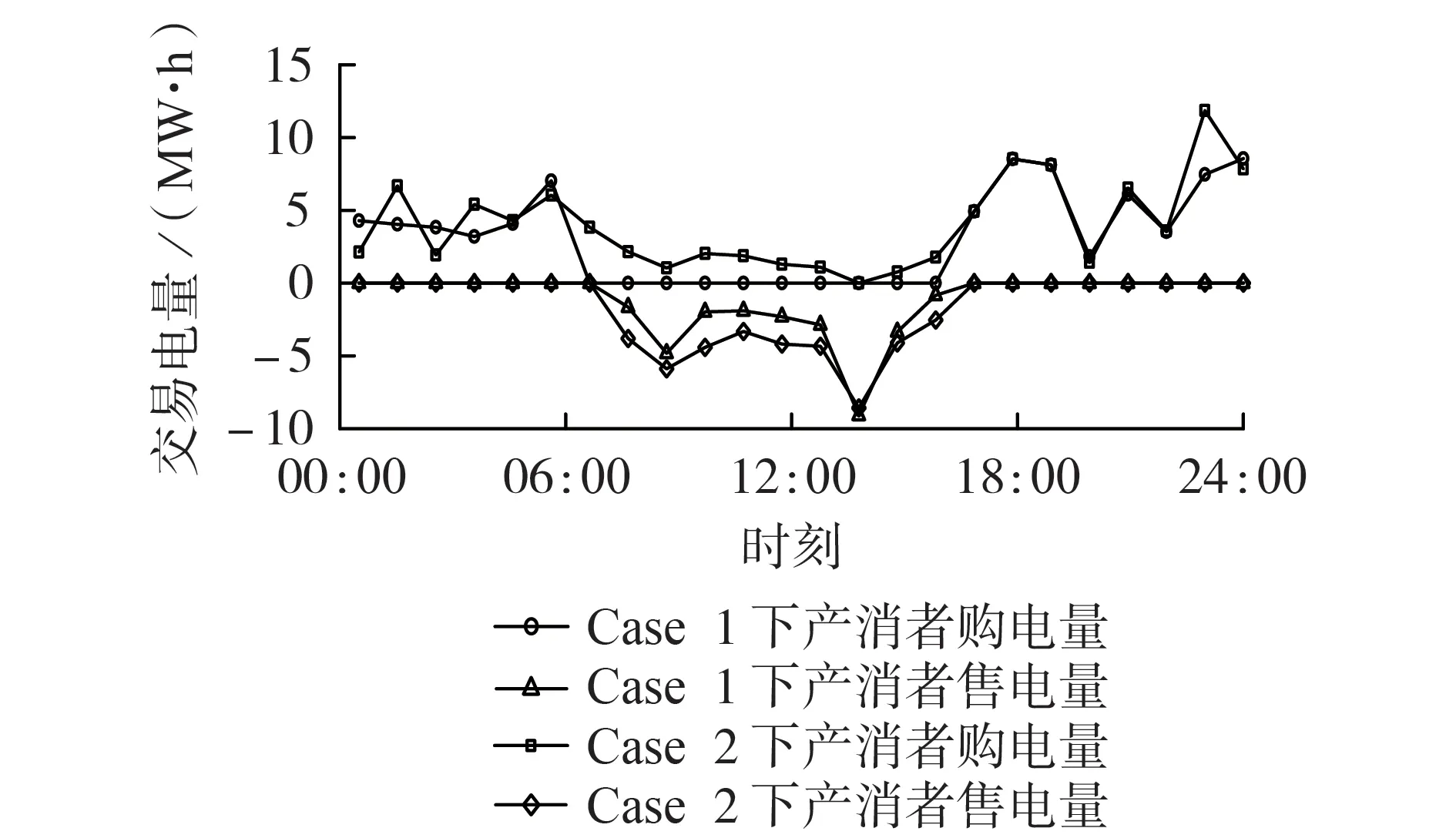
图2 2种算例下产消者与MO的交易电量Fig.2 Energy trading between prosumers and MO under two cases

2 种算例下07:00、09:00 以及19:00 这3 个时刻产消者的市场交易策略如附录D 图D2 所示。在07:00，Case 1 下3 个产消者仅通过彼此间的分散交易即可满足自身的电能交易需求；在09:00，Case 1下存在多种交易模式，产消者1 以分散交易的形式向产消者3购入1.05 MW·h的电能，产消者2以集中交易的形式向MO 出售3.05 MW·h 电能，而产消者3同时参与集中与分散交易，分别将1.78 MW·h 和1.05 MW·h 的电能出售给MO 和产消者1；在19:00，产消者均处于供不应求状态，2种算例下产消者的交易策略完全一致，即仅通过集中式交易向MO购电。

2 种算例下联盟运行成本见表1。与Case 2 相比，Case 1下产消者与MO的交易成本降低10472元。然而，由于产消者间交易需要额外支付服务费用，因此，分散交易的成本增加4 840 元。整体来看，相较于集中交易机制，集中-分散协同交易机制可降低约8.67%的运行成本。

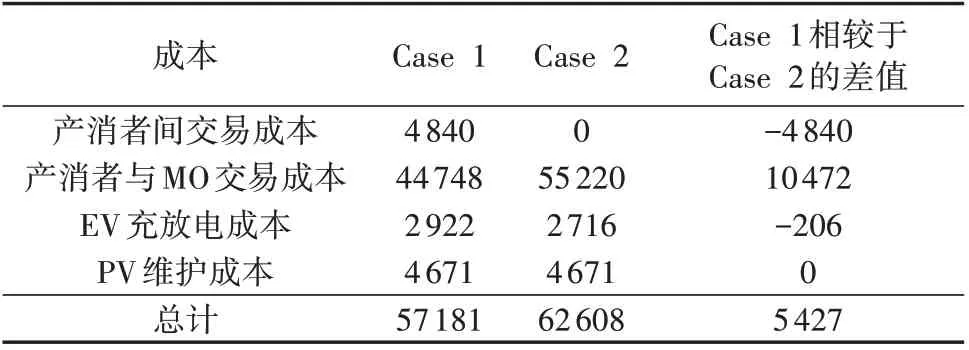
表1 2种算例下联盟运行成本Table 1 Operation cost of alliance under two cases单位：元

若由于线路传输容量限制，产消者与MO 的单笔交易电量最高为2.5 MW·h，则超过该交易值会产生一定的弃光量。以多电产消者2 为例，在不同算例下，其向MO的售电量曲线如图3所示。由图可以看出，Case 2下产消者2向MO的售电量整体高于Case 1，且在Case 1 下的弃光现象仅发生在15:00，弃光量较少，而Case 2 下，在10:00、14:00、15:00 均有不同程度的弃光量产生。可见，当产消者之间可以进行P2P 交易时，多电产消者可以灵活选择其交易对象，并使得清洁能源以及剩余电能尽可能地在联盟内部消纳。

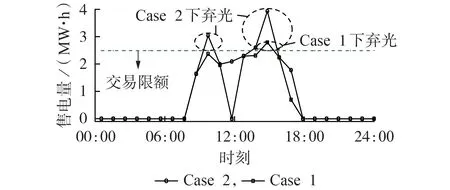
图3 产消者2向MO售电量曲线Fig.3 Electricity sales curve of Prosumer 2 to MO

3.2.2 Nash谈判有效性分析

为验证所提基于Nash 谈判法的收益分配策略的有效性，在各产消者整体参与市场交易的情况下，设置以下不同利润分配方法：方法1，按Shapley值法进行收益分配；方法2，按Nash 谈判法进行收益分配，不考虑各产消者的风险偏好程度；方法3，按Nash 谈判法进行收益分配，考虑各产消者的风险偏好程度。3 种方法下各产消者的运行成本如表2 所示，表中初始谈判值表示各产消者单独参与市场交易的运行成本。

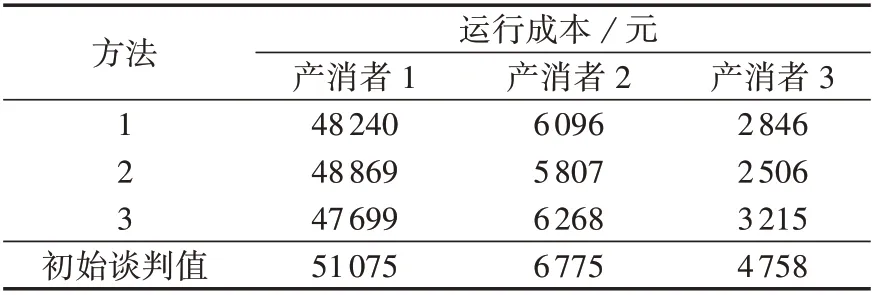
表2 3种方法下各产消者的运行成本Table 2 Operation cost of each prosumer under three methods

由表2 可知，无论采用哪种分配方法，各产消者的运行成本均低于初始谈判值，这说明了Nash 谈判法能够保证产消者间的收益分配结果位于核中。对比方法1 和方法2 可知，相较于Shapley 值法，由于Nash 谈判法进一步考虑了平均供需比对分配策略的影响，因此平均供需比较高的产消者2和产消者3能够在该谈判中获得更高的收益。对比方法2 和方法3 可知，在考虑各方的风险偏好后，对风险抵御能力更强的产消者1 收益有了较大提高，而风险抵御能力较差的产消者2和产消者3的收益则有所降低。由此可见，本文采用的Nash 谈判分配方法能够从多个角度衡量各产消者的市场力水平，避免因按单一指标分配而出现收益分配不均的问题，体现了竞争市场环境下收入分配的公平性。

3.2.3 鲁棒保守度参数对产消者交易结果的影响

为探究PV 出力波动影响下产消者交易策略的变化，分别设置鲁棒模型的保守度为0、1、3、6，以产消者2为例，其与MO的交易策略如图4所示。

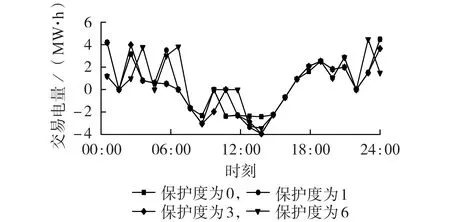
图4 不同保守度下产消者2的市场交易策略Fig.4 Market trading strategy of Prosumer 2 under different conservatisms

由图4 可见，PV 出力的不确定性对产消者的市场交易策略有一定的影响，主要体现在当PV波动性较大时，产消者需要出售／购买更多的电量以保证电能供需的平衡，而PV波动性较小时，产消者与MO的交易电量则相对较低。因此，在产消者市场交易模型中，有必要采用鲁棒优化方法对交易过程中的不确定因素进行处理。

此外，鲁棒交易模型的保守度参数对联盟整体的运行成本也有一定的影响，如图5 所示。由图可知，随着保守度参数的不断增大，模型的不确定性逐渐增加，多产消者的整体运行成本也逐步提高，即多产消者联盟在制定日前调度计划时越多考虑PV 出力的不确定性，得到的方案就越保守，相应的运行成本也越高。

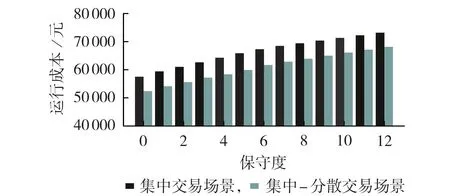
图5 不同保守度下多产消者运行成本Fig.5 Operation cost of multiple prosumers under different conservatisms

附录D 表D1 给出了不同预测误差下多产消者整体运行成本。在同一保守度参数下，随着预测误差的增大，无论是在集中交易还是集中-分散交易场景下，多产消者整体的运行成本都有较大幅度的增加，且随着Γi的提高，预测误差对运行成本的影响更为明显。

3.2.4 C&CG算法性能测试

为探究产消者数量对本文所提算法的影响，对比产消者数量分别为1、3、5、10这4种情况下的算法计算结果，如表3 所示。由表可见，在不同产消者数量下，C&CG 算法均能够通过少量的迭代次数使得模型收敛到最优解。值得注意的是，随着产消者数量的增多，主问题和子问题的规模也随之扩大，对应的离散变量、连续变量及约束数量也成倍增加，这导致每次迭代的计算时间增加，但对于包含10 个产消者的算例系统，其最终的计算时间也仅为963.48 s，这对于日前交易／调度而言是满足要求的。附录D表D2给出了不同类型产消者对算法的影响，由表可见，改变产消者的类型对算法的迭代过程几乎无影响，但是在包含互补类型产消者的算例系统中，产消者的整体运行成本更低。

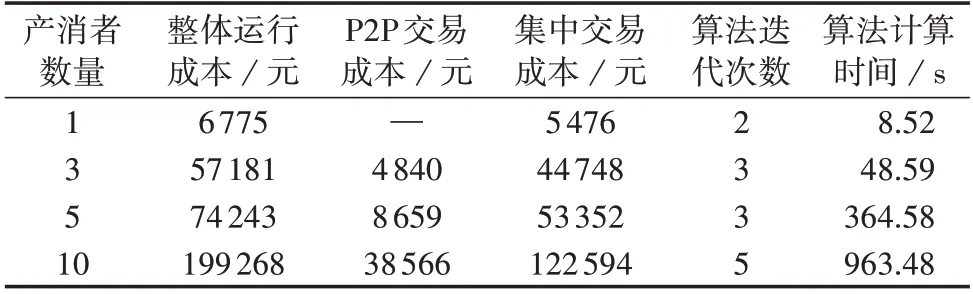
表3 不同产消者数量下C&CG算法计算结果对比Table 3 Comparison of calculation results of C&CG algorithm under different numbers of prosumers

4 结论

本文针对多产消者集中-分散交易过程中的不确定性问题，提出一种多产消者两阶段鲁棒集中-分散交易模型，基于算例测试结果得出以下结论。

1）通过将多产消者两阶段鲁棒交易模型分解为交易状态组合主问题以及不确定因素影响下的经济调度子问题，并利用C&CG 算法交替迭代主问题以及子问题，可实现模型的高效求解。经测试可知，即使是包含10 个产消者的算例系统，最终的求解时间也仅为963.48 s，满足日前交易／调度的要求。

2）集中-分散交易模式能够通过产消者之间的P2P交易减少产消者整体与MO 的交互功率，保证了交易策略的灵活性，促使多电产消者的电能尽可能地在系统内部消纳，显著提高了整体经济效益，相较于集中交易模式，能够降低约8.67%的运行成本。

3）相较于仅考虑贡献度的Shapley值法，Nash谈判法考虑了多个产消者的风险偏好、边际贡献以及供需比等因素，且设置谈判破裂点以保证分配结果一定位于核中，评价指标更为全面，分配策略更加科学，且模型的求解较为简单。

4）不确定因素对产消者的交易策略有一定的影响。通过改变鲁棒模型的保守度，能灵活调整多产消者交易策略的保守性，且各产消者可通过提高PV预测精度进一步提高自身参与市场交易的竞争力。

本文仅关注多产消者日前交易策略的制定，并未涉及实时交易策略，后续笔者将在日前交易策略的基础上，进一步深入研究多产消者的实时交易策略，从而构建更加完整的产消者市场交易体系。

附录见本刊网络版（http：//www.epae.cn）。