基于图形处理器加速的电网全网拓扑分析算法
郑逸凡,周 赣,傅 萌,王子恒,冯燕钧
(1. 东南大学 电气工程学院,江苏 南京 210096;2. 中国电力科学研究院有限公司,江苏 南京 210003)
0 引言
电网拓扑分析是根据开关元件的状态,归并电网中用于分析计算的拓扑节点(计算节点),并识别相互孤立的电气岛的分析计算方法,是开展稳态分析、状态估计、安全分析等电网分析计算的基础[1-2],可抽象为一张给定图G=(V,E)(V为节点集,E为支路集)的多次连通性分析问题。目前,随着电网规模的扩大以及电力系统互联水平的提高,电网拓扑分析的计算量显著上升,对国调某时刻断面采用传统的串行算法进行电网拓扑分析,耗时已经达到1.27 s[2]。此外,后续电网分析计算整体计算量的增加,也对拓扑分析的实时性提出了更高的要求。
近年来,有关电网拓扑分析加速的研究主要集中在局部拓扑修正[3]方面,但局部修正在长期运行中,尤其是多次执行之后,会导致置信度低和优化排序被破坏等问题[4]。此外,在实际的运行过程中,电网分析计算软件需要定期重新进行全网拓扑分析,以排除局部拓扑修正失效的可能。因此,只有改进全网拓扑分析,才能从根本上加快电网拓扑分析的速度。然而,对全网拓扑分析的加速技术(如扩充邻接节点[5]、追踪技术[6]、面向对象技术[7])的研究受制于直接搜索法的时间复杂度O(n+m)(n为节点数量,m为支路数量)瓶颈,只能通过减少相对不关心的环节来进行加速。引入分布式计算和并行计算有助于绕过瓶颈,提高电网拓扑分析计算过程的效率[5]。文献[2]对图进行划分后,尝试采用共享存储并行编程OpenMP(Open Multi-Processing)对划分的子图进行并行广度优先搜索,利用厂站间的并行性取得了一定的加速效果,但算法并未利用厂站内的并行性。事实上,文献[2]中方案的加速比在线程数量增加至12 个后便已达到饱和,限制其性能的原因是内存交互的时间成本,若进一步挖掘厂站内的并行性,更多的内存交互可能反而导致加速比下降。
近年来,图形处理器GPU(Graphics Processing Unit)作为一种具有高内存带宽和强浮点计算能力的新型并行处理器,逐渐被应用于大规模电力系统分析的加速计算中,在潮流计算[8]、状态估计[9]、静态安全分析[10]、电磁暂态仿真[11]、用电负荷预测[12]等应用场合已经有显著的加速表现,使单一模块的计算耗时降低到60 ms 以下[8-12]。显然,配套高效GPU 并行拓扑分析算法的缺失,已经成为限制上述并行加速计算应用的主要障碍。因此,基于以下2点原因,有条件也有必要探索基于GPU 的全网拓扑分析算法:①随着网络规模的增大,传统中央处理器CPU(Central Processing Unit)算法不能满足实时性要求,常规加速方法的效果有限,而GPU 具有高加速潜能;②GPU 全网拓扑分析能够与已完成的GPU电网分析加速算法形成闭环,放大其加速效果。
目前,GPU 领域对拓扑分析问题的研究主要关注理论层面的通用图论算法,鲜有涉及面向电网特征的拓扑分析算法。文献[13]提出了著名的前驱数组法(也称平方法),采用前驱数组代替序列在广度优先搜索算法中的作用,实现了广度优先搜索算法的并行化加速;文献[14]进行混合方向优化,解决了前驱数组法在首端和末端并行度不足的问题;文献[15]提出了一种细粒度拓扑分析方法,使GPU并行算法的时间复杂度也能渐近达到O(n+m)。上述并行图论算法对加速电网拓扑分析具有参考价值,但电网拓扑除了具有图的普遍性质外,还具有来源于物理规律和电网建设要求的特征,若将上述图论算法直接应用于电网拓扑分析,则无法充分挖掘电网拓扑分析问题中的并行性。例如,电网拓扑分析的厂站间存在并列关系,节点间的并行性集中分布在母线节点上。以厂站为单元划分电网,并设计细粒度访问方案挖掘母线节点的并行性,便可在GPU 通用方法的基础上,实现针对电网的进一步加速。因此,本文主要进行了如下工作。
1)提出一种基于电网自然划分和细粒度线程控制的并行厂站拓扑分析方法。首先,在图划分法的基础上,以厂站间输电线路为划分割集,将各厂站拓扑解耦,省略了边界协调步骤,实现了GPU 算法对厂站间并行性的挖掘;然后,在GPU 算法过程中,利用厂站内计算负载主要分布在母线节点的特性,设计了GPU线程资源在单个厂站拓扑分析中的成组分配方式,优化了GPU算法对厂站内并行性的挖掘。
2)提出一种分厂站压缩存储电网结构模型。该模型以公共信息模型CIM(Common Information Model)为基础,应用“压缩-索引”技术优化了上述并行厂站拓扑分析方法的矢量化访存模式。
3)以并行厂站拓扑分析方法为核心,提出了一种基于GPU加速的大规模电网全网拓扑分析算法。
以华东电网某时刻断面为算例进行测试,分析结果表明,本文所提算法适用于不同规模的电网,采用本文算法分析含34110个拓扑节点系统的全流程计算用时为42.246 ms,其加速比分别为串行直接搜索法、8线程多线程算法的7.242倍、2.148倍。
1 电网拓扑分析问题的建模
1.1 电网拓扑图模型
IEC61970 定义了能量管理系统EMS(Energy Management System)的应用程序接口,CIM 作为该标准的重要组成部分,以面向对象的方式定义了信息交换的语义。CIM 规定拓扑包,其中电网的具体信息被抽象为无向图形式,电网中每个实际元件的电气连接点被称为连接节点或物理节点,通过开关与刀闸相连的物理节点集合被称为拓扑节点。通过输电线路、变压器等构成电气联系的设备相连的拓扑节点集合被称为电气岛[16]。由CIM抽象得到的电网无向图G的模型可以表示为式(1)—(4)所示常见的节点-支路模型,包含节点集V和支路集E的无向图拓扑结构见附录A图A1。


式中:Ai为第i个节点的邻接表。
1.2 电网拓扑分析方法
电网拓扑分析的总体流程如图1 所示,主要包括厂站拓扑分析和网络拓扑分析2 个部分。厂站拓扑分析是在每个厂站内,沿着无向图的连接边进行搜索,将全部物理节点归并到拓扑节点下,并进行双向标识的过程。网络拓扑分析是在全网范围内,沿着无向图的连接边进行搜索,将全部拓扑节点归并到电气岛下,进行双向标识并判别和计算主岛信息的过程。除此之外,电网拓扑分析还包括数据准备和结果出口步骤。厂站拓扑分析和网络拓扑分析是电网拓扑分析的主要可加速部分,也是本文研究工作的重点对象,其余部分的执行顺序影响结果的正确性和编号的稳定性,依赖CPU单线程串行执行。

图1 电网拓扑分析的总体流程Fig.1 Overall process of power grid topology analysis
广度优先搜索算法是厂站拓扑分析和网络拓扑分析的基础算法之一[8],其在效率上比深度优先搜索算法更适用于电网[7]。广度优先搜索算法的核心是维持一个在访问过程中逐步生成和排空的序列Q。以厂站拓扑分析为例,依次访问Q中的物理节点,并将被访问物理节点的邻接物理节点添加到序列的最后,直到Q被清空,则完成了一个拓扑节点的分析。此时继续在电网中寻找下一个未被访问过的物理节点:如果存在该物理节点,则以其为起点,开始另一个拓扑节点的划分;如果不存在该物理节点,则结束厂站拓扑分析。广度优先搜索算法在网络拓扑分析中的应用方式与上述过程类似。
2 电网拓扑分析的并行化
2.1 电网拓扑压缩存储模型
以节点-邻接表形式存储的电网无向图的邻接表是分散保存在内存中的,GPU 无法对其进行有效读取。基于文献[18]中“压缩-索引”的思想,即使GPU各线程访问时能够分别矢量化访问而不发生读写冲突,将这些邻接表按节点编号顺序首尾相连,生成一个索引表用于记录各节点邻接表的起止位置。
将以节点-邻接表形式存储的电网无向图的各邻接表首尾相连,并保存其起始位置,使电网无向图G被抽象为节点集V、压缩邻接数组Acsr及其索引数组IAcsr,如式(7)所示。
G=(V,Acsr,IAcsr) (7)
电力系统各厂站之间存在天然的并行关系,为了挖掘厂站间的并行性,采用类似的方式将电网中每个厂站的节点表Sk(k=1,2,…,l;l为电网中厂站的数量)连缀成压缩厂站节点表Scsr,并为其编制索引数组IScsr,使式(8)所示分散保存厂站信息的电网无向图G转换为式(9)所示的压缩数组形式。上述电网无向图的转换过程见附录A图A2。

2.2 并行广度优先搜索算法
为了保持广度优先搜索算法的分层性和结果唯一性,广度优先搜索算法并行加速的关键为解决并行计算语境下序列Q的建立和维护问题。以前驱数组法[13]为基础的并行广度优先搜索算法采用不断更新的数组F代替串行算法中的序列Q。以厂站拓扑分析为例,F的长度等于电网中的物理节点总数,数组元素与物理节点一一对应,元素值为0 时表示该物理节点在下层拓扑分析中不需要被访问,元素值为1 时表示该物理节点在下层拓扑分析中启动,且归属于当前拓扑节点。将数组F中启动物理节点的邻接点对应元素值置为1,相当于在串行算法中将邻接点压入序列Q,直至数组F中所有元素值均为0,则完成当前拓扑节点的分析。
并行广度优先搜索算法挖掘了位于同层的物理节点之间的并行性。虽然线程间可能出现竞争和拥塞现象,但可以被证明是良性的[19]。文献[13-15]表明,基于前驱数组法的并行广度优先搜索算法在社交网络拓扑分析和路网拓扑分析中表现良好。但电网拓扑分析问题具有特殊性,除了同层物理节点间存在并行关系之外,还存在如下并行性可被挖掘。①电网中厂站之间的并行性。在解决线程恶性竞争问题且不影响算法结果唯一性的前提下,各厂站可并行开展拓扑节点划分。②电网中各节点的邻接点之间的并行性。电网中少数物理节点(一般为母线节点)具有大量的邻接点,若调整计算资源,使线程分配方案适应不均匀的计算负载,则能够快速获得并行性。
2.3 改进并行厂站拓扑分析算法
2.3.1 基于厂站划分的线程竞争规避
为了挖掘2.2节所述并行性①,在厂站拓扑分析中,考虑对电网中的各厂站同时进行拓扑节点划分,但由于并行算法中线程是并发且无序的,直接假设多个起点并划分不同的拓扑节点,将导致恶性线程竞争,使拓扑分析结果严重错误。
解决不规则图并行结果正确性问题的常用方法是使用原子操作。原子操作通过锁定线程的访问权限,以保证并行拓扑分析算法的正确性。然而,原子操作的效率一般是比较低的,且当并行度较高,同时访问某一内存地址的线程较多时,原子操作将引发严重的拥塞问题。文献[19]进一步提出了2 种规避原子操作的方法:一种为解耦法,适用于计算任务间互相不依赖的算法;另一种为代数法,适用于线程工作在同一张数据表、计算任务相互依赖的算法。但多个起点的并行广度优先搜索算法是一种混合算法。一方面,前驱数组的每一位与一个线程唯一对应,前驱数组自身是解耦的;另一方面,对于多个起点所激活的不同线程群,读取邻接表数据和写入结果均在同一内存空间内进行,是相互依赖的。
为了在多起点并行广度优先搜索算法中规避原子操作的使用,本文利用电网接线特性,预先对输入的电网进行自然划分,具体步骤如下:
1)省略邻接数组中的输电线路信息,将电网划分为以厂站为单位的子网(这种划分对于GPU 而言是不可知的);
2)省略邻接数组中的变压器信息,将厂站内的子网划分为不同的电压等级;
3)并行开展厂站拓扑分析;
4)记录每个厂站划分拓扑节点的总数,将其作为每个厂站的偏移量;
5)计算各拓扑节点考虑偏移量后的节点编号,得到唯一的厂站拓扑分析结果。
电网无向图的自然划分示意图如图2 所示,由于输电线路和变压器被省略,不同厂站间的拓扑节点划分是解耦的,并行算法不再需要在全网范围内保持同步。在每个厂站任选一个起点独立进行拓扑节点划分,即使没有外部信息输入或线程之间的信息交互,也不会发生恶性线程竞争,保持了结果的唯一性。

图2 电网无向图的自然划分示意图Fig.2 Natural division diagram of power grid’s undirected graph
2.3.2 基于细粒度线程控制的计算负载均衡
采用前驱数组法进行厂站拓扑分析,若遵循数组元素、线程、物理节点相对应的线程分配原则,则会导致在电网厂站拓扑分析中少数线程的计算负载过大(一般是母线节点对应的线程),同层的电网末端节点对应的线程访问1~2 个物理节点之后就陷入等待,造成了计算资源的浪费。因此,为了挖掘2.2节所述并行性②,本文依据GPU 的计算通用设备架构CUDA(Compute Unified Device Architecture)特点,对线程进行重分配。
CUDA 引用了单指令多线程SIMT(Single Instruction Multiple Threads)的并行模式对线程进行执行和管理。CUDA 中的GPU 包含大量的基础单元,这些单元被称为核(core),多个核集成在一起被称为多流处理器SM(Streaming Multiprocessors),每台SM 能在物理上同时处理的线程数量等于核数量。在物理上能同时被处理的线程被组织为线程束(warp),在逻辑上并行的多个线程被组织为线程块(block),大量线程块被组织为网格(grid)[20]。在通常情况下,1 个网格可以容纳65 535 个线程块,1 个线程块可以支持的逻辑上并行的最大线程数量为512 个,1 个线程束可支持的物理上同时执行的线程数量为32个。
以华东电网为例,根据2.3.1 节进行厂站划分后,厂站内物理节点数量的分布结果如表1 所示。可见,厂站包含的物理节点数量远小于GPU 中每个线程块支持的最大线程数量,支持为每个物理节点的计算负载分配更多的块内线程资源。在本文所用算例中,每个厂站平均包含29.75个物理节点。

表1 某电网厂站内物理节点的数量分布Table 1 Number distribution of physical nodes in a power grid’s substations
一般而言,选取GPU 内部运行参数为2x(x为任意非负整数)有利于提高并行算法的整体性能,设定如下参数:

即,每个线程块包含128 个线程,以4 个线程为1 组,可分为32 个线程组,每个线程组对应厂站中的1 个物理节点。电网中的每个厂站有128 个线程分担其计算任务,厂站中的每个物理节点有4 个线程分担其计算任务。
改进前驱数组法计算负载分配示意图见附录A图A3。前驱数组法的计算任务主要集中在线程1—4,导致下层线程5—12 延迟启动。若将节点1—4的计算任务分配给其对应线程组的线程1—16,则各线程来自上层的等待耗时显著降低,本层的计算负载也得到了均衡。此外,随着搜索层数的加深,每层计算任务均衡分配的范围变大,增加了计算过程中的并行度。
在厂站内对任意一个物理节点进行搜索的步骤如下:
1)该物理节点的线程监测到物理节点对应的前驱数组元素值被修改为1,启动相应的线程组;
2)线程组的线程0—3 并行读取该物理节点的压缩邻接数组的索引数组,形成该物理节点的邻接表;
3)线程组的线程0 修改该物理节点的前驱数组元素值为0,读取该厂站当前拓扑节点的划分进度,并将该节点划分进当前拓扑节点;
4)线程组的线程0—3 依次遍历该物理节点的4个邻接节点,扩展前驱数组;
5)线程组的线程0 检查该物理节点是否有未被访问的邻接节点,若有则返回步骤3),否则结束对该物理节点的搜索。
3 算法实现
3.1 并行厂站拓扑分析
改进并行厂站拓扑分析算法包含线程竞争规避和计算负载均衡,本文分两部分实现算法求解,其中GPU 部分为并行厂站拓扑分析核函数;CPU 部分为偏移计算模块,其功能为整理GPU 分析结果,并赋予各个拓扑节点唯一编号。算法伪代码见附录B 算法1,该算法挖掘了以下并行性:
1)物理节点邻接表各元素之间的并行性;
2)同层物理节点之间的并行性;
3)电网各厂站之间的并行性。
3.2 并行网络拓扑分析
网络拓扑分析的基本原理与厂站拓扑分析一致。此外,电网中的拓扑节点数量一般小于物理节点数量,网络拓扑分析的计算量相较于厂站拓扑分析较小,本文所用算例电网的计算规模见附录C表C1。
网络拓扑分析涉及全网拓扑节点和厂站间的联系。全网拓扑节点总数大于线程块所能包含的线程数量,算法1 不能为每个拓扑节点分配多个线程,因而不能挖掘拓扑节点邻接表各元素之间的并行性。厂站之间相互联系,使得厂站不再并列,厂站之间的并行性消失。因此,无法使用算法1 的改进算法,本文采用前驱数组法进行网络拓扑分析,算法伪代码见附录D 算法2。算法2 作为并行网络拓扑分析算法,挖掘了广度优先搜索算法中同层拓扑节点之间的并行性。显然,与算法1 相比,算法2 挖掘的并行性不足,但随着电网规模的增大,理论上算法2 可以逐渐展现优势,实现网络拓扑分析的并行加速。
3.3 时间复杂度分析

进行电网拓扑分析时,划分拓扑节点和电气岛的功能操作同样耗时,因此估计串行直接搜索算法的实际时间复杂度为O((n+m)lg(n+m)),并行算法的实际时间复杂度也会受到类似的影响。对于算法1 而言,由于物理节点分布相对均匀,物理节点间支路密度高,能够实现较为有效的并行加速;对于算法2 而言,由于主岛的拓扑节点数量明显多于其余孤岛的拓扑节点数量,拓扑节点间支路密度低,p趋近于1,算法2对网络拓扑分析的加速有限。
4 算例分析
4.1 测试条件
为了验证算法1和算法2的实际运算性能,基于算例对并行厂站拓扑分析和网络拓扑分析算法的优劣进行辨析。选取华东电网不同工况下工作断面文件作为算例进行电网拓扑分析,包括算例case1281、case3472、case5208、case34110,不同算例包含的最低电压等级不同,其中case34110包含的最低电压等级为1 kV。算例的基本参数信息见附录E表E1。算例测试采用的软件环境为:Microsoft Visual Studio 2015(V140)和NVIDIA CUDA 10.0,运行在Linux凝思4.2.32操作系统上。算例测试硬件环境如下:CPU型号为Intel Core i9-9900K,运行主频为3.60 GHz,内存为32 GB;GPU 型号为NVIDIA TITAN RTX。为了验证本文所提GPU 加速算法的正确性和计算效率,选用智能电网调度控制系统(D5000)串行单线程网络拓扑分析函数,并复现文献[2]所述并行多线程图划分法作为验证算法。其中,智能电网调度控制系统的版本为V3.0,配套商用数据库管理软件为达梦6.0。
4.2 正确性测试
为了确保测试结果的正确性,将CPU 并行图划分法[2](简称为CPU算法)和基于GPU加速的电网全网拓扑分析算法(简称为GPU 算法)与智能电网调度控制系统V3.0 串行单线程网络拓扑分析函数算法(简称为D5000 算法)进行对比,结果如表2 所示。由表可知,GPU 算法和CPU 算法的全网拓扑分析结果与D5000 算法的拓扑分析结果一致,与现行电网调度控制系统中的串行网络拓扑分析算法等效,满足后续电网分析计算的工程应用要求。

表2 不同算法的拓扑分析结果比较Table 2 Comparison of topology analysis results among different algorithms
4.3 效率测试


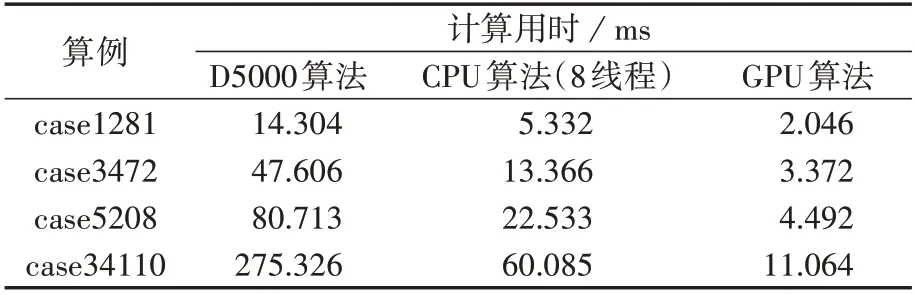
表3 不同算法的厂站拓扑分析计算用时比较Table 3 Comparison of calculation time of substation topology analysis among different algorithms
GPU 算法、CPU 算法、D5000 算法的网络拓扑分析计算用时对比如表4所示,表中结果为3次计算用时的平均值,CPU 算法的计算用时计及了图划分引入的边界协调耗时,GPU 算法的计算用时计及了GPU加速引入的数据准备与传输耗时。

表4 不同算法的网络拓扑分析计算用时比较Table 4 Comparison of calculation time of network topology analysis among different algorithms
由表4 可知:本文所提基于前驱数组法的GPU算法能够取得的加速效果有限,采用GPU 算法分析算例case34110 时相比D5000 算法仅取得了1.136 倍的加速比,且当算例规模不够大时,几乎得不到加速。经计算,3 种网络拓扑分析算法的时间复杂度均约为O((n+m)1.05),D5000 算法、CPU 算法和GPU算法在划分电气岛等功能操作的影响下,时间复杂度略大于O(n+m),且CPU 算法和GPU 算法的并行度p都接近1,并行加速效果不明显。上述测试结果与3.3 节的时间复杂度分析结果相符。造成上述现象的原因在于:网络拓扑分析仅挖掘了同层拓扑节点间的并行性;电网中连通拓扑节点的输电线路或变压器的密度低,所挖掘的同层拓扑节点间的并行性低;电网主岛包含了大多数的拓扑节点,拓扑节点分布不均匀,使综合并行度p趋近1;对于算例case34110而言,网络拓扑分析仅涉及了3.4×104个拓扑节点,D5000 算法对于该类规模系统的网络拓扑分析也具有不错的运算性能。
为了验证本文所提全网拓扑分析算法的实时性与正确性,采用上述算例和测试平台进行全网拓扑分析测试。不同算法的全流程计算用时对比如表5所示,表中数据为3 次计算用时的平均值。由表可知:对于规模较大的算例case34110 而言,相比D5000算法,本文所提GPU 算法能够取得7.242倍的加速比;相比CPU 算法,本文所提GPU 算法也能取得2.148倍的加速比。可见,采用本文所提算法进行全网拓扑分析能显著加快拓扑分析过程的速度,且算例规模越大,加速效果越好。

表5 不同算法的全流程计算用时对比Table 5 Comparison of whole process calculation time among different algorithms
不同算法的拓扑分析用时占总计算用时的比例如图3 所示。由图可知:当采用D5000 算法时,厂站拓扑分析与网络拓扑分析用时占总计算用时的比例为82%~91%;而采用本文所提GPU 算法时,随着算例规模的增大,电网拓扑分析用时所占比例逐渐降低到25%以下,突破了拓扑分析算法的时间复杂度瓶颈。
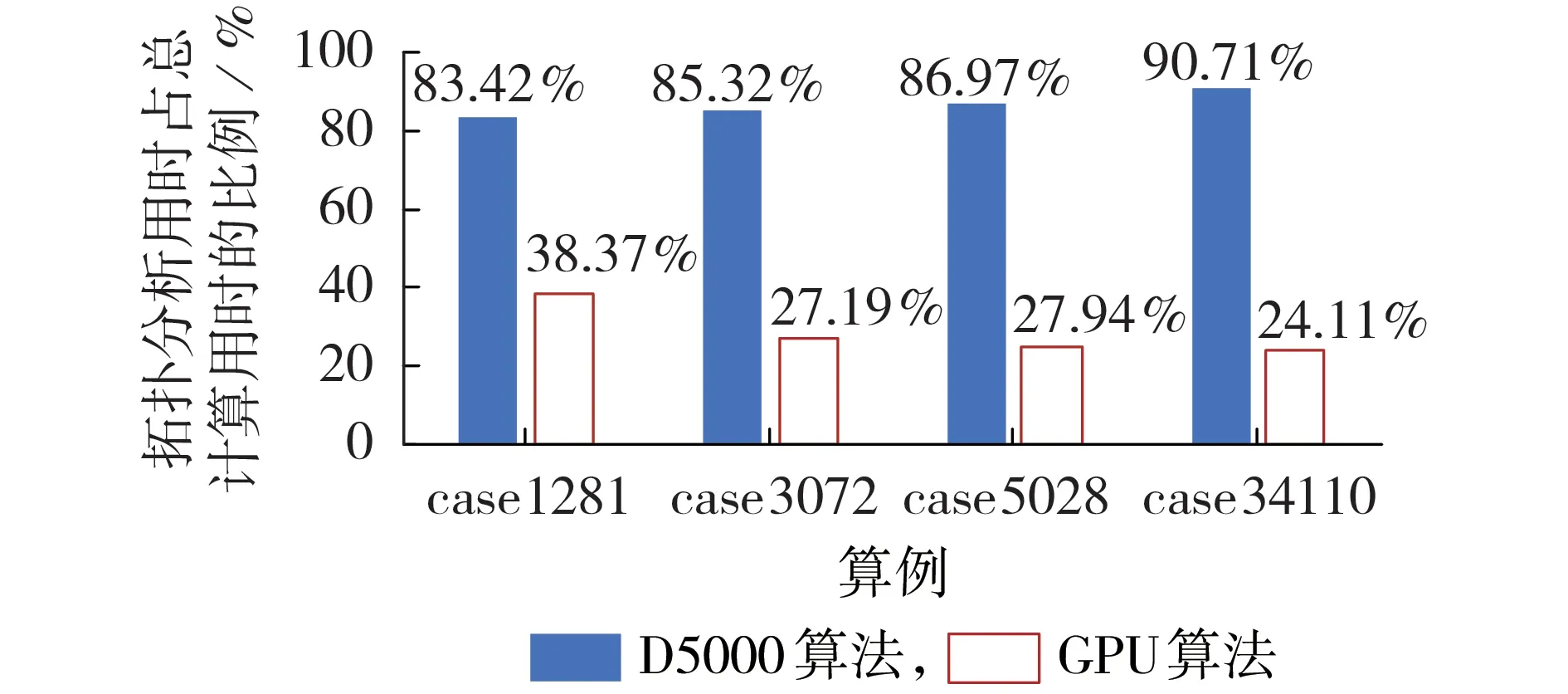
图3 不同算法的拓扑分析用时占总计算用时的比例Fig.3 Proportion of topology analysis time to total calculation time for different algorithms
综上可以看出,本文所提GPU 算法用于全流程取得的加速效果不如用于并行厂站拓扑分析取得的加速效果,这是因为测试算例中涉及的电网规模过大,依赖CPU 单线程处理的各计算模块的计算用时显著增大,无法加速的CPU 部分的计算用时占比升高,从而降低了GPU 部分取得的加速效果。各模块的计算用时如表6所示。

表6 采用GPU算法时各模块计算用时Table 6 Calculation time of each module based on GPU algorithm
对于其中的网络拓扑分析而言,由于该部分的计算用时较小,虽然本文所提GPU 算法取得的加速效果一般,但不影响其整体的性能,算法的性能瓶颈最终落在CPU 执行部分。为了后续进一步提升算法性能,应在全网拓扑分析的问题建模和数据处理方面进行更深入的研究。
5 结论
本文提出了一种基于GPU 加速的电网全网拓扑分析算法,以前驱数组法并行广度优先搜索为基础,并非专注于算法层面的并行性挖掘,而是立足于实际电网满足的物理规律和建设要求进行并行性挖掘,结合电网的特点进行了多层并行性的优化挖掘,能正确、快速、有效地对电网进行全局拓扑分析,并向后续功能模块出口分析结果。
算例测试结果表明,本文所提算法能够显著加快全网拓扑分析中厂站拓扑分析部分的执行速度,进而加快算法出口拓扑节点分析结果和划分电气岛的速度,有利于电力系统中部分分析计算整体效率的提升。所提算法加速的瓶颈落在串行执行的数据处理及传输部分,在后续研究过程中,有必要将本文所提电网拓扑分析算法与其他基于GPU 加速的电网分析算法进行对接,省略数据传输与转化时间,以取得更好的加速效果。
附录见本刊网络版(http://www.epae.cn)。

