绝对值三角不等式及其应用

任 宏

(内蒙古北方重工业集团有限公司第三中学，014030)

绝对值三角不等式是一类特殊的不等式,它反映的是实数和与差的绝对值和绝对值的和差之间的关系,是处理含绝对值问题的重要工具,在许多问题中都有着重要的应用.

一、绝对值三角不等式的几何背景

绝对值三角不等式的几何背景就是关于向量的三角不等式|a|-|b|≤|a+b|≤|a|+|b|.实际上，用向量a，b替换实数a,b时，问题就从一维扩展到二维.(1)当向量a，b不共线时，a+b，a，b构成三角形，由三角形两边之和大于第三边可知|a|-|b|<|a+b|<|a|+|b|.(2)当向量a，b共线时，若a，b同向(相当于ab≥0)，则|a+b|=|a|+|b|,若a，b反向(相当于ab<0)，则|a+b|<|a|+|b|.

二、绝对值三角不等式的推广

(1)把三角不等式中的两个实数相加推广到两个实数相减，得到|a|-|b|≤|a+b|≤|a|+|b|.

(2)推广到多个实数相加，则有|a1+a2+…+an|≤|a1|+|a2|+…+|an|,当且仅当a1,a2,…,an同号或至少有一个为零其余同号时等号成立.

三、应用举例

1.求解最值问题

绝对值三角不等式常用来处理与最值有关的问题,重点是多个绝对值之和(差)的问题.在应用时,要把a±b变为常数,同时等号能取到.

例1若关于x的不等式|x-1|-|x+4|≤|t+1|有解，记实数t的最大值为T.

(1)求T的值；

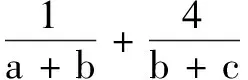
解(1)因为|x-1|-|x+4|≤|(x-1)-(x+4)|=5,x=-5时取等号，故(|x-1|-|x+4|)max=5.

又由|x-1|-|x+4|≤|t+1|有解，可得|t+1|≤5,解得-6≤t≤4.

故实数t的最大值T=4.

评注第(1)问首先利用绝对值三角不等式求得|x-1-|x+4|的最大值,然后将不等式|x-1|-|x+4|≤|t+1|有解转化为关于t的绝对值不等式求解，从而得到结论.求解的关键是不要将“不等式|x-1|-|x+4|≤|t+1|有解”与“不等式|x-1|-|x+4|≤|t+1|恒成立”混淆,否则就会出现错误.

例2已知函数

f(x)=|x+3|-|x-1|.

(1)解关于x的不等式f(x)≥x+1;

(2)若f(x)的最大值为M,a>0,b>0,且(a+1)(b+1)=M,求a+b的最小值.

解(1)(-∞,-5]∪[-1,3].(过程略)

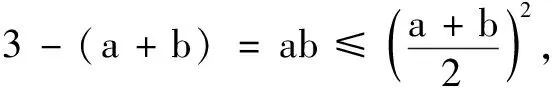
评注第(2)问利用绝对值三角不等式求得函数f(x)的最大值M是解题的基础,比分类讨论去掉绝对值符号解题更简便.

2.证明不等式

用绝对值三角不等式证明不等式时,要对绝对值内的式子进行分拆、重组、添项、减项等配凑变换,使要证明式子与已知之间联系起来,方便解题.

例3已知a,b,c为正实数，且满足a+b+c=1.证明：

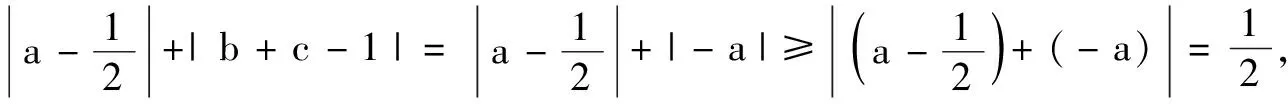
(2)略.

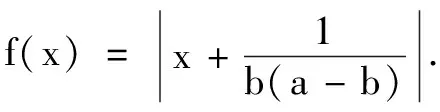
(2)求证:f(x)+|x-a2|≥4.

解(1)(-∞,-6)∪(-2,+∞).(过程略)

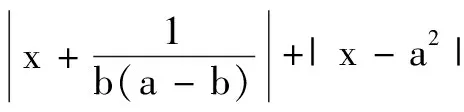
3.求参数的取值范围

利用绝对值三角不等式求参数的取值范围,首先是由绝对值三角不等式求得最值,然后转化利用最值法来求解.在利用最值法求解时,要注意不等式恒成立和不等式有解这两者之间的区别.

例5(2020年全国高考题)已知函数f(x)=|x-a2|+|x-2a+1|.

(1)当a=2时，求f(x)≥4的解集;

(2)若f(x)≥4,求a的取值范围.

解(1)略

(2)由绝对值三角不等式,得f(x)≥|(x-a2)-(x-2a+1)|=|-a2+2a-1|=(a-1)2(当且仅当2a-1≤x≤a2时取等号)，所以f(x)min=(a-1)2.

因为f(x)≥4,所以f(x)min≥4,即(a-1)2≥4,解得a≤-1或a≥3.

故a∈(-∞,-1]∪[3,+∞).

评注本题第(2)问是不等式的恒成立问题,在利用绝对值三角不等式求得f(x)最值后,转化利用最值法求解.不等式恒成立问题求解原理是:若a≥(或>)f(x)对x∈D恒成立，则a≥(或>)f(x)max;若a≤(或<)f(x)对x∈D恒成立，则a≤(或<)f(x)min.

例6已知函数f(x)=|2x+a|-a.

(1)当a=2时，求不等式f(x)≤4的解集；

(2)若不等式f(x)-|2x-1|≥3的解集非空，求a的取值范围.

解(1)[-4,2].(过程略)

(2)f(x)-|2x-1|=|2x+a|-|2x-1|-a.由绝对值三角不等式，得|2x+a|-|2x-1|≤|(2x+a)-(2x-1)|=|a+1|,所以f(x)-|2x-1|≤|a+1|-a.

因为f(x)-|2x-1|≥3的解集非空，即不等式f(x)-|2x-1|≥3有解，所以|a+1|-a≥3,即|a+1|≥3+a.

当a+1≥0,即a≥-1时，a+1≥3+a,有1≥3,不成立.

当a+1<0,即a<-1时，-(a+1)≥3+a,解得a≤-2.

故a的取值范围为(-∞,-2].

综上可见,对于含多个绝对值的不等式或最值问题,若能根据问题特征灵活使用绝对值三角不等式,可以简化问题的求解过程,使问题轻松获解.