系杆拱桥合理成桥状态研究分析
焦明东,高 敏,宋 玉,司 奎
(上海同济检测技术有限公司,上海市200092)
0 引言
不同吊杆力对系杆拱桥成桥状态的影响较大,成桥状态的合理与否直接关系到桥梁合理施工阶段的确定及成桥运营阶段的安全。作为外部静定、内部有水平推力的超静定结构,系杆拱桥体系受力复杂,结构受力和线形影响因素多[1-3]。很多学者对系杆拱桥合理成桥状态展开了研究:以刚性支承连续梁法为基础,以系杆截面弯矩合理为目标,虞建成[4]等提出了吊杆张拉力新的确定方法,能够快速实现吊杆张拉力在期望目标下的求解。以拱肋和系杆应变能极小化为目标,刘钊[5]提出了合理吊杆力的三种计算方法:刚性吊杆法、无限轴向刚度法和二次规划法。以影响矩阵法为基础,张熙胤[6]等提出以最小结构应变能为目标函数的无约束吊杆力优化算法,实现了较好的吊杆力优化效果。以拱肋恒载弯矩分布最优为目标,以吊杆力为变量,任亮[7]等采用影响矩阵法对某拉索组合拱桥实现了良好的吊杆力优化效果。
综合上述研究,目前对于系杆拱桥合理成桥状态研究,多集中在吊杆力优化等方面,缺少针对系杆拱桥合理成桥状态的系统研究,基于此,拟在研究系杆拱桥合理成桥状态和实现方法的基础上,依托实际工程案例,对比分析不同理论下的合理成桥状态,然后从吊杆力、拱肋和系杆内力及系杆位移方面进行对比分析,结果显示相对刚度变化法得到的成桥状态最为合理。
1 系杆拱桥合理成桥状态
1.1 总体思路
刚性拱肋、柔性系杆是当前系杆拱桥设计的优先选择。对于系杆拱桥,吊杆主要起传递桥面系荷载的作用,一端连接系杆,对系杆提供向上的拉力;另一端连接拱肋,将桥面系荷载和吊杆自重传递给拱肋,拱肋水平方向的推力由系杆承担,竖向方向的力传递给支座[9]。对于系杆拱桥而言,不同吊杆力对应不同的结构受力状态,因此寻找合理的成桥状态,在一定程度上是在寻找合理成桥吊杆力。确定合理成桥状态[2]的总体思路如下。
(1)首先确定系杆(包括主梁纵桥向)结构的合理受力状态;
(2)根据系杆结构的合理受力状态,确定吊杆的合理成桥状态,即确定吊杆力大小,从而确定桥面系对主拱肋的作用;
(3)将拱肋自重、吊杆力施加在主拱肋上,计算得到拱肋的压力线,如果桥梁拱轴线无限接近于压力线,则认为拱轴线的选择是合理的。
综上所述,合理成桥状态确定的内容包括系杆合理成桥状态的确定、合理吊杆力的确定和合理拱轴线的判断。
1.2 系杆合理成桥状态
根据结构优化理论[9],索结构优化的理论基础是结构弯曲应变能最小原理。从结构受力而言,系杆拱桥属于梁拱组合体系桥梁,除主拱处于受压状态外,系杆主要是作为拉弯构件。为了节约系杆材料,一般情况下应以恒载作用下系杆弯矩最小为合理受力状态;根据相关研究[10-13],系杆处于正负弯矩交替状态时弯矩应变能纵梁最小。
1.3 吊杆力合理成桥状态
吊杆力是系杆拱桥合理成桥状态的重要内容,它既决定了系杆的受力状态,又是影响拱轴线的重要因素,其大小与分布影响着整个结构体系的受力状态;合理成桥吊杆力应当保证成桥状态下系杆某种受力性能指标(如弯矩、应力等)达到最优,除边吊杆外,各吊杆的吊杆力应大致相等。
1.4 拱肋合理成桥状态
合理吊杆和系杆受力状态下,要求各种荷载组合中,主拱截面弯矩极值尽量降低,最好能够保证主拱全截面均匀受压。考虑到恒载作用占总荷载作用比重较大、活载作用下弯矩包络图上下对称的特点,因此恒载作用下的拱肋压力线与拱轴线无限接近则是拱肋合理成桥状态。
2 工程背景
2.1 工程概况
某钢管混凝土系杆拱桥,拱肋净跨102.0 m,矢高20.0 m,矢跨比为1/5.1,主拱轴线采用二次抛物线,见图1 所示。桥梁宽为20.5 m,拱肋间距19.0 m,桥面宽度为17.5 m。单片拱肋共设18 根吊杆,吊杆间距5.0 m。拱肋截面采用哑铃形钢管混凝土截面,竖向由2 根Φ1 000.0 mm 钢管构成,总高2.6 m。系杆采用钢箱型断面,宽1.5 m,高2.0 m,壁厚20.0 mm。

图1 拱桥总体布置图(单位:cm)
2.2 有限元模型
采用通用有限元软件建立空间杆系模型。拱肋和系杆采用梁单元,吊杆采用只受拉桁架单元。桥面铺装和护栏等桥面系结构按照等效荷载施加。全桥划分为805 个梁单元,36 个桁架单元,630 个节点。每个节点位置的截面都按实际结构尺寸输入,模型边界按照实际情况施加,有限元模型见图2 所示。

图2 有限元模型
2.3 模型分析过程
对于系杆拱桥,一次落架的施工过程,系杆将分担更多的荷载,该状态下对应的吊杆力分布接近于理想吊杆力优化状态,即为合理成桥状态。以下模拟分析过程均采用一次落架方法模拟。
2.3.1 刚性支承连续梁法
对于系杆拱桥,恒载和吊杆力共同作用下,以系杆在吊杆纵桥向前后正负弯矩均匀、交替出现为目标,将吊杆作用视为竖向刚性支承,各支点反力即为合理成桥吊杆力。有限元模型中,删除吊杆,在主梁吊点位置设置竖向刚性支承,施加恒载即可得到恒载作用下的成桥吊杆力,此吊杆力对应系杆拱桥合理成桥状态下的吊杆力。2.3.2 最小弯曲能量法
最小弯曲能量法在求合理成桥状态时,是以结构整体的弯曲应变能最小为控制目标。对于一次落架的系杆拱桥,可将拱肋、系梁和吊杆的轴向刚度赋以足够大的值或者将拱肋和系梁截面抗弯刚度赋予足够小的值,恒载作用下即可实现弯曲应变能最小,即认为桥梁实现合理成桥状态。
2.3.3 相对刚度变化法
相对刚度变化法原理是系杆拱桥在一次落架时,随着系杆与拱肋相对刚度的变化,吊杆力会发生相应的改变,拱肋、系杆的内力状态也会发生相应的改变。在模型中,可将拱肋抗弯惯性矩增大到1 000倍或将系杆的截面惯性矩减小至1/1 000,对恒载作用下的整体模型进行一次落架分析,使得结构弯曲应变能不变,而轴力、剪力引起的能量趋于最小,即得合理成桥状态。
3 计算结果
3.1 吊杆力
鉴于系杆拱桥的吊杆力在纵桥向、横桥向的对称性,选择1/4 吊杆进行对比分析,不同理论下成桥吊杆力计算结果见表1 所列。
根据表1 成桥吊杆力对比分析可知:

表1 成桥吊杆力对比分析表 单位:kN
(1)刚性支承连续梁法求得的吊杆力,最大值为1 319 kN,为1# 吊杆;最小值为612 kN,为2# 吊杆,3#~9# 吊杆的吊杆力均为691 kN,最大值与最小值之间吊杆力差别较大,长吊杆的吊杆力相对均匀。
(2)最小弯曲能量法求得的吊杆力,最大值为639 kN,为9# 吊杆;最小值为480 kN,为1# 吊杆,吊杆力最大值与最小值之间差别较大;吊杆力变化范围为480~639 kN,变化幅度较大。
(3)相对刚度变化法求得的吊杆力,最大值为873 kN,为1# 吊杆;最小值为688 kN,为3# 吊杆;除1# 吊杆外,其余吊杆的吊杆力在688~692 kN 之间,吊杆力相对均匀。
3.2 结构内力
分别将刚性支承连续梁法、最小弯曲能量法和相对刚度变化法计算得到的吊杆力,以体外力形式施加到模型中,一次落架得到拱肋弯矩分布见图3所示,系杆弯矩分布见图4 所示。

图3 拱肋弯矩分布图(单位:kN·m)

图4 系杆弯矩分布图
根据图3 可知,拱脚处弯矩相对较大,拱顶处弯矩相对较小,对比不同模拟方法可得到如下结论:
(1)刚性支承连续梁法,拱肋最大弯矩为2 719kN·m,位于1#吊杆与2#吊杆之间;最小弯矩为-836 kN·m,位于拱脚位置。
(2)最小弯曲能量法,拱肋最大弯矩为14 614 kN·m,位于拱脚位置;最小弯矩为-945 kN·m,位于拱顶位置。
(3)相对刚度变化法,拱肋最大弯矩为2 550 kN·m,位于拱脚位置;最小弯矩为645 kN·m,位于拱脚与1# 吊杆之间,拱肋弯矩分布相对均匀,且没有负弯矩产生。
根据图4 可知,拱脚处系杆产生部分负弯矩,系杆跨中正弯矩最大,对比不同模拟分析方法可以得到如下结论:
(1)刚性支承连续梁法,系杆最大弯矩为1 604kN·m,位于跨中位置;最小弯矩为-1 501 kN·m,位于拱脚位置。
(2)最小弯曲能量法,系杆最大弯矩为6 552 kN·m,位于系杆中间位置,最小弯矩为-15 691 kN·m,位于拱脚位置。
(3)相对刚度变化法,系杆最大弯矩为1 681 kN·m,位于跨中区域;最小弯矩为-3 982 kN·m,位于拱脚位置;除开拱脚段,其余系杆弯矩均为正值,从1# 吊杆向跨中位置逐渐增大。
3.3 结构位移
分别将刚性支承连续梁法、最小弯曲能量法和相对刚度变化法计算得到的吊杆力,以体外力的形式施加到模型中,得到成桥结构位移见表2 所列。根据表2 成桥结构位移对比,可得如下结论:
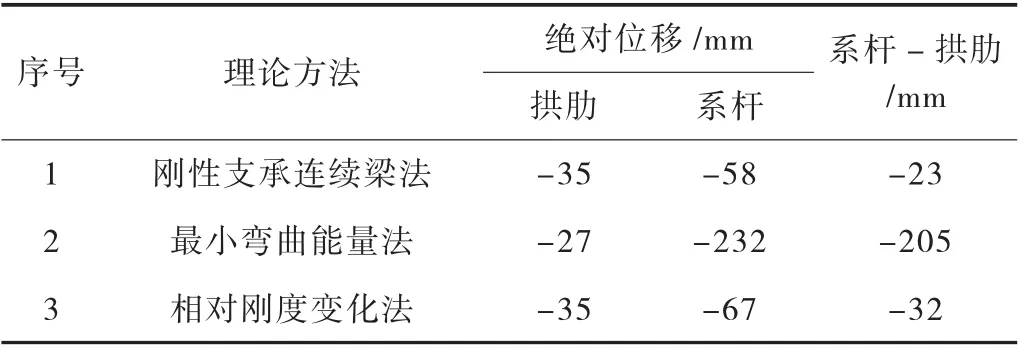
表2 成桥结构位移对比分析表
(1)刚性支承连续梁法,拱肋最大位移为-35 mm,位于拱顶位置,系杆最大位移为-58 mm,位于系杆中心处,系杆与拱肋相对位移为-23 mm。
(2)最小弯曲能量法,拱肋最大位移为-27 mm,位于拱顶位置,系杆最大位移为-232 mm,位于系杆中心位置,系杆与拱肋相对位移为-205 mm。
(3)相对刚度变化法,拱肋最大位移为-35 mm,位于拱顶位置,系杆最大位移为-67 mm,位于系杆中心位置,系杆与拱肋相对位移为-32 mm。
4 结 论
合理成桥状态的确定是系杆拱桥施工和监控量测的基础。基于合理成桥的详细分析和不同实现方法的介绍,结合实际工程案例,通过有限元模拟得到如下结论:
(1)刚性支承连续梁法除短吊杆的吊杆力异常外,其余吊杆力分布、结构(拱肋、系杆)内力分布和系杆位移方面均能满足系杆拱桥对于合理成桥状态的要求,但需要基于系杆弯矩对于短吊杆的吊杆力进行优化。
(2)最小弯曲能量法在吊杆力分布、结构(拱肋、系杆)内力分布和结构位移方面均不适用于系杆拱桥成桥状态确定。
(3)相对刚度变化法无论从吊杆力分布、结构(拱肋、系杆)内力分布,还是从拱肋、系杆位移方面,均能够满足系杆拱桥对于合理成桥状态的要求。
本文从不同实现方法、不同结构响应方面对比分析了刚性支承连续梁法、最小弯曲能量法和相对刚度变化法在系杆拱桥合理成桥状态确定中的适用性,能够对未来系杆拱桥的设计选型、监控量测和运营维护提供一定的理论和工程经验。

