例谈“学、教、评”视角下的数学题研究

陈芝飞, 谢尚志

(温州市第十四高级中学，浙江 温州 325000；温州市第二十二中学，浙江 温州 325001)

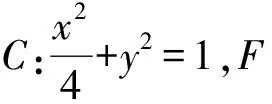
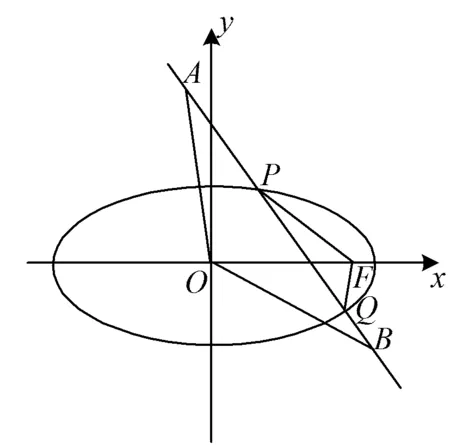
图1

1)试用x1表示|PF|；

2)证明：原点O到直线l的距离为定值.

(2020年浙江省温州市数学第二次模拟考试第21题)

1 学生视角下的解题

1.1 第1)小题

问题1已知条件是什么？

问题2求什么？

两点间的距离|PF|.

问题3怎么求？

利用两点间距离公式，代入化简，求得|PF|.

1.2 第2)小题

问题4任务是什么？

证明原点O到直线l的距离为定值.

问题5如何证明原点O到直线l的距离为定值？

问题6如何找到m与k的关系式？

合理利用条件|PA|=|PF|,|QB|=|QF|,|OA|=|OB|.

问题7以上这些条件如何利用？是直接翻译还是等价转化？如何转化？

2)注意到点A,B在直线l上，加之目标是寻找m与k的关系，故需引进点A,B的坐标A(xA,yA)，B(xB,yB),并用斜率表示|PA|,|QB|，即

3)若直接翻译，则式子很复杂，不利于条件整合，需要等价转化.两边相等的常用等价方式是什么？

问题8转化后的条件如何整合？

1)建立x1,x2与m，l的关系.

2)建立xA,xB与x1,x2的关系.

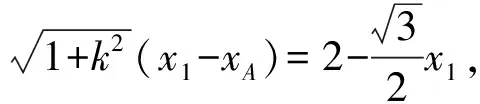
(1)

(2)

3)寻找m与k的关系式.

式(1)+式(2)，得

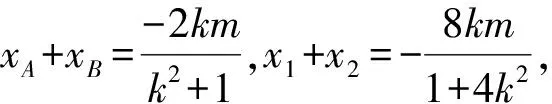
整合化简得

m2=k2+1.

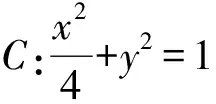
(1+4k2)x2+8kmx+4m2-4=0,

从而

于是

又点A,P,Q,B从上到下依次排列，于是

2 教师视角下的说题

学生视角下的解题重在一道题目的解决，体现的是解题素养，这只是研题的第一阶段.更为重要的是“教”,即教师视角下的说题，包含3个方面：说解题难点及教学对策；说题目背后核心素养的培育；说题目变式，探寻题目的源与流.

2.1 说解题难点及教学对策

例题的难点在哪里？首先是明解题方向：寻找m,k的关系；其次是寻解决之法：如何合理利用并有效转化“3对相等线段”的条件，建立m,k的关系；最后是探实施之道：明算理、优方法，理解解析思想，提升运算能力.

面对这些解题中的难点，我们日常教学中有哪些对策呢？

首先，教师要树立正确的解题教学理念.解题教学要关注解题思想，而不是表面上眼花缭乱的“N”种解法.教师要将自己在解题过程中的所思所想提炼成数学解题思想，转化为教学设计，以问题的形式呈现给学生，让学生重现思考过程，感受解题技法背后的数学解题思想，最终帮助学生形成基于学科核心素养的解题思想[1].

其次，明算理、优方法，重视数学运算能力的培养.先确定“寻找m,k的关系”作为解题目标，并围绕这一目标进行数量关系的建立和转化，反映的是基于解析思想的“明算理”意识；学生对条件“3对相等线段”是直接翻译还是合理转化反映的是“优方法”能力；在“明算理、优方法”后，是否能最终解决问题，反映的是数学运算的能力.搞清楚了这些问题之后教学对策就更清晰了——缺什么，补什么，如此才能做到精准施教.

最后，还要追求数学本质，重视概念教学.例1本质上是考查解析思想，这与教材的要求是一致的.李邦河院士指出：数学本质上是玩概念的.高考历来重视概念教学，注重能力立意，渗透素养考查，高考的导向是引导中学遵循教学规律，教授数学本质，教导学生掌握数学方法，发展数学能力，提升数学核心素养.然而教师的“拔苗助长”，使得师生遨游在茫茫题海中，“二级结论满天飞、一入题海误终生”，高中数学课堂教学渐渐演变为“题型教学”，题型教学又进一步蜕化为“刺激—反应”训练的状况[2].殊不知这样会给学生增加许多不必要的负担，学生渐渐失去了学习的兴趣，最终既不利于学生能力的发展，也不利于学生成绩的提高.

2.2 说题目背后核心素养的培育

解题教学中应关注哪些核心素养的培育呢？首先，要重视培育学生会用数学眼光观察世界，比如直观想象能力，帮助学生直观分析“如果原点O到直线l的距离为定值，那么直线l是定圆的切线”，为了说明这一点，需要寻找m,k的关系；再比如，根据“三线段相等”可以直观想象△PQF的周长等于线段|AB|的长，那么直线l变化中线段|AB|的长是否保持不变？其次，要重视培育学生会用数学思维分析世界：逻辑推理、数学运算.比如，|OA|=|OB|如何解析？|PA|=|PF|,|QB|=|QF|如何翻译？转化后的条件如何整合？如何建立x1,x2与m,k的关系？如何建立xA,xB与x1,x2的关系？如何寻找关于m与k的关系式？基于数学学科核心素养，如何把知识的学术形态转化为教育形态？如何挖掘数学内部资源实现数学的育人功能？这些问题是值得每一位数学教育工作者不懈追求的课题[1].

2.3 说题目变式，探寻题目的源与流

2.3.1 关于一般椭圆的结论

(b2+a2k2)x2+2kma2x+a2m2-a2b2=0,

(3)

代入式(3)，化简得

即

故原点O到直线l的距离为定值b.

2.3.2 弱化条件|PA|=|PF|,|QB|=|QF|

|PA|+|QF|=|PF|+|QB|，

代入化简，得

(4)

其余同变式1(略).

2.3.3 椭圆与圆的关系

(b2+a2k2)x2+2kma2x+a2m2-a2b2=0,

其中m2=b2(1+k2),进一步化简，得

另一方面，由|PF|=a-ex1，|QF|=a-ex2，知

故△PQF的周长=|PF|+|QF|+|PQ|=2a.

通过变式1～4发现：当直线y=kx+m(其中km<0)与圆x2+y2=b2相切时会有一系列的特殊性质，因此直线l：y=kx+m(其中km<0)与圆x2+y2=b2相切是题源所在.那么除了变式4，还会呈现哪些有趣的题流呢？

2.3.4 例1的几何背景

(证明可参见变式3.)

进一步可以得到以下诸多猜想结论:

如此下去，还有更多题流可以挖掘.

3 评价视角下的命题

3.1 现数学之美

3.2 体现素养考查导向

在高考由单纯的考试评价向立德树人重要载体和素质教育关键环节转变的背景下，考试的教育功能将更加凸显.在评价理念上，实现了高考由传统的“知识立意”“能力立意”评价向“价值引领、素养导向、能力为重、知识为基”综合评价的转变.在评价模式上，实现了高考从主要基于“考查内容”的一维评价模式向“考查内容、考查要求、考查载体”三位一体评价模式的转变.

那么，解析几何的命题评价要体现哪些素养呢？需要考查逻辑思维能力、运算求解能力、创新能力等关键能力；考查理性思维、数学探索、数学文化等3类学科素养；设置探索创新情境考查学生知识迁移、应用能力及创新能力，凸显能力立意，避免平时常说的解析几何“设、联、消、韦、判”的程式化套路；重在考查解析思想及明算理、优方法的数学解题思想.

3.3 展现命题隐与巧

通过教师说题研究、探清题目的源与流之后便能运用自如地“编题”了[3].现在反过来审视例题我们发现:巧妙地将△PQF的周长隐藏在线段AB中，利用“直线l：y=kx+m(其中km<0)与圆x2+y2=b2相切时，△PQF的周长为定值2a”的性质设置例题，展现了命题的隐与巧，如果是一个小题(如选择题)，则还可以这样命制：

( )

A.|PF2|+|PQ|=|PF1|

B.|PF1|+|PQ|=|PF2|

C.|QF2|+|PQ|=|PF1|

D.|QF2|+|PF1|=|PQ|

评注将km<0及原点O到直线l的距离为定值b巧妙地隐藏在直线l：sinθ·x-cosθ·y-1=0中.

4 构建三维视角下的研题模式

基于以上3个维度的实践探究，我们认为数学研题应该做到“学生、教师、评价”点线面兼顾，全方位一体化思考；既要学会以学生的视角解题，还要掌握以教师的视角说题，最后才能以评价的视角命题.在实践探究过程中，经过总结提炼构建了三维视角下的研题模式(如图2).其中，学：学生视角的解题是基础，要先让学生会解题；教：教师视角的说题是核心，标志着从解题走向解题教学；评：评价视角的命题是关键，既是对“学”的评价，又是对“教”的引领.“学、教、评”三维视角下的研题相互作用，互为支撑，具有一站式、立体化的特点，无论对教师专业发展，还是对“减负提质”都有着积极的借鉴意义.

图2