波形钢腹板组合工字梁的振动特性

张紫辰， 王根会， 樊 江

(1.兰州交通大学 土木工程学院，兰州 730070； 2.甘肃省交通规划勘察设计院股份有限公司，兰州 730070)

波形钢腹板组合工字梁具有良好的力学性能，目前已广泛应用于中国、法国和日本等国家的土木工程建设之中[1-3]。与平钢腹板桥梁相比，波形钢腹板抗剪性能优越，具有更高的面外刚度及较强的景观美感，同时波形钢腹板的褶皱效应也提高了预应力施加效率，有效解决了温度应力和徐变等因素带来的结构病害[4-6]，因此波形钢腹板组合梁是当前土木建设的热门之一，具有广阔的发展前景。然而，这种组合工字梁在对称弯曲时，其翼缘板内弯曲正应力呈现不均匀分布，即存在剪力滞后现象，受剪力滞后和腹板褶皱效应的影响，波形钢腹板组合工字梁的弯曲力学性能求解较为复杂[7]。近年来，众多学者针对其静力特性开展了大量研究，部分研究成果已在组合梁的设计中得到应用[8-11]。针对波形钢腹板组合工字梁的振动问题也有相关文献报道[12]，但研究方向主要集中在自由振动方面，关于这类结构强迫振动问题的研究较少，且既有文献均未同时考虑Timoshenko剪切变形、转动惯量、剪滞翘曲应力自平衡条件以及腹板褶皱效应等多重因素对结构振动特性的影响，因而其计算具有一定的局限性。由于结构的振动频率是计算其动力特性的基础[13]，而结构在地震荷载作用下的破坏也主要源于强迫振动，所以较为准确地分析波形钢腹板组合工字梁的振动特性十分重要。

本文基于能量变分法和Hamilton原理，综合考虑上述多重因素的影响，推导出组合工字梁的动力学弹性控制微分方程和自然边界条件，利用有限元分析结果验证了本文方法的准确性，结合数值算例详细分析了组合工字梁的振动特性。本文理论为该类组合结构振动特性的精细化分析提供了新方法，对该类结构的设计具有一定的指导意义。

1 组合工字梁振动控制微分方程

1.1 组合工字梁的势能和动能

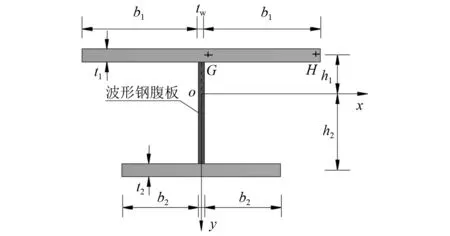
波形钢腹板组合工字梁截面如图1所示。图1中：b1为上翼板宽度；b2为下翼板宽度；t1为上翼板混凝土厚度；t2为下翼板混凝土厚度；tw为波形钢腹板厚度；h1和h2分别为上翼板和下翼板到形心轴的距离；y轴为组合工字梁的高度方向；x轴为组合工字梁的宽度方向。

图1 波形钢腹板组合工字梁Fig.1 Composite I-beam with corrugated steel webs

在对称弯曲状态下设结构的跨度为l，结构的竖向动挠度为w(z,t)，则剪力滞效应引起组合梁上、下翼板的翘曲位移可表示为[14]

ς1(x,y,z,t)=[α-yf1(x)]u1(z,t)

(1)

ς2(x,y,z,t)=[α-yf2(x)]u2(z,t)

(2)

式中：f1(x)和f2(x)分别为组合工字梁上、下翼板不均匀分布函数，且f1(x)=cos[(πx)/(2b1)]；0≤x≤b1；f2(x)=cos[(πx)/(2b2)];0≤x≤b2；u1(z,t)和u2(z,t)为结构振动时剪力滞效应引起的组合梁上、下翼板的纵向动位移差函数；α为组合梁上、下翼板各自满足应力自平衡条件求得的常数之和。

则组合工字梁上、下翼板应力分别翼板

(3)

(4)

下翼板

(5)

(6)

则组合工字梁上、下翼板变形势能为

(7)

整理变换，V1可表示为

(8)

其中,

组合工字梁剪切应变能为

(9)

波形钢腹板有效剪切模量Gw为[15]

(10)

式中：L1为平板长度；L2为斜板长度；δ为波折角；Es为钢材弹性模量；υs钢材泊松比。

组合工字梁荷载势能为

(11)

组合工字梁总势能为

V=V1+V2+V3

(12)

结构总动能为

(13)

1.2 振动微分方程及自然边界条件

(14)

(16)

(17)

相应的自然边界条件为

(18)

(19)

(20)

(21)

1.3 振动微分方程求解

根据组合工字梁的振动特点，若结构振动圆频率为ω，则有

q(z,t)=q0(z)sin(ωt+φ)

(22)

同时，可令

w(z,t)=W(z)sin(ωt+φ)

(23)

u1(z,t)=U1(z)sin(ωt+φ)

(24)

u2(z,t)=U2(z)sin(ωt+φ)

(25)

θ(z,t)=Ο(z)sin(ωt+φ)

(26)

式中,φ为组合工字梁强迫振动时的初始相位角。

(27)

对式(27)进行分析可知，其特征方程的解为

r1,2=±n1,r3,4=±n2,r5,6=±n3,r7,8=±n4

根据微分方程的性质，可得式(27)的通解为

W(z)=C1ch(n1z)+C2sh(n1z)+C3ch(n2z)+C4sh(n2z)+

式中，C1～C8为待定常数，可由相应边界条件求得。

由常微分方程组性质和恒等式原理，最终可得O(z)的方程解为

(29)

同理可得U1(z)和U2(z)的方程解为

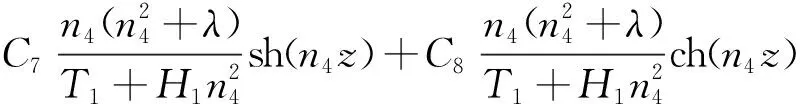
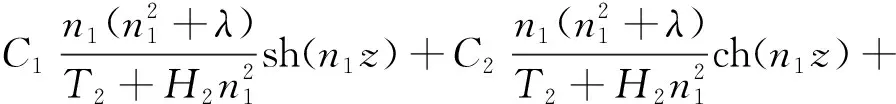
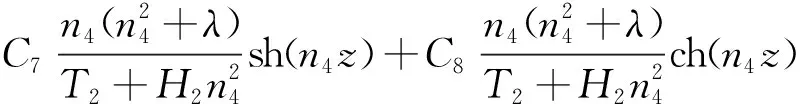
1.4 常用边界条件

(1)简谐均布力作用下两端简支组合工字梁边界条件为

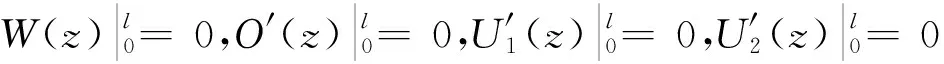
对于两端简支组合工字梁，若跨间r点作用1个简谐集中力Pr=P0sin(ωt+φ)，且集中力Pr距左右边界距离为l1和l2，如图2所示。则r点需引入的连续边界条件为

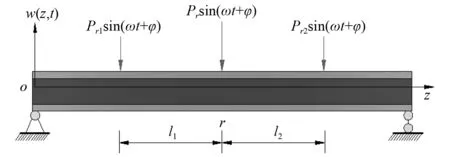
图2 坐标及荷载系统Fig.2 Coordinate and load system

(33)

式中：U11和U12分别为工字梁纵向原点和简谐集中力作用点处上翼板最大纵向翘曲动位移差函数；U21和U22分别为工字梁纵向原点和简谐集中力作用点处下翼板最大纵向翘曲动位移差函数。

(2)简谐均布力作用下两端固支组合工字梁边界条件为

对于两端固支组合工字梁，若跨间r点作用1个简谐集中力，且集中力Pr距左右边界距离为l1和l2，则r点需引入的连续边界条件同式(33)，若为多个简谐集中力，则按单个简谐集中力计算后将结果进行叠加。

在求解组合工字梁的自振频率时，令均布简谐力q(z,t)=0，将式(28)～式(31)或其求导式代入相应的边界条件，可以得到结构的固有频率方程，再通过MATLAB软件求解其特征值方程，从而得到结构的各阶振动圆频率ωn，将组合工字梁振动的圆频率转化成竖向自振频率，计算式为

(35)

1.5 振动方程的退化

(1)为了体现剪滞翘曲应力自平衡对组合工字梁振动特性的影响，对本文振动方程进行退化，得到不考虑剪滞翘曲应力自平衡影响的传统剪力滞理论(双翘曲动位移差函数)振动微分方程为

(36)

(38)

(39)

相应的自然边界条件为

(40)

(41)

(42)

(43)

(2)为了体现剪力滞效应对组合工字梁振动特性的影响，将传统剪力滞理论振动方程进一步退化，得到不考虑剪力滞效应影响的Timoshenko梁理论振动微分方程为

(44)

(45)

相应的自然边界条件为

(46)

(47)

对于传统剪力滞理论和Timoshenko理论的振动微分方程的求解方法同上，不再详述。

2 算 例

如图1所示波形钢腹板组合工字梁，梁高1.3 m，其上、下翼板均采用C50混凝土，ρc=2 600 kg/m3，厚度t1=t2=0.15 m，上翼板宽b1=1.6 m，下翼板宽b2=0.8 m；波形钢腹板厚度为1.8 cm，ρs=7 800 kg/m3，直板L1=6.25 cm，斜板L2=6.23 cm，波折角δ=37°，力学分析中简谐集中力幅值为9 800 N。

根据文献[17]的建模方法，采用ANSYS 15.0软件建立波形钢腹板组合工字梁有限元模型，如图3所示，其中混凝土采用Solid65单元模拟，波形钢腹板选用Shell63单元模拟，同时增加目标单元TARGE170和接触单元CONTA175，以实现钢混连接部位的MPC(Multipoint Constraints)多点耦合接触，这样可对顶、底板和腹板独立划分网格，从而保证了模拟的精度。

图3 有限元模型及局部网格Fig.3 Finite element model and mesh generation

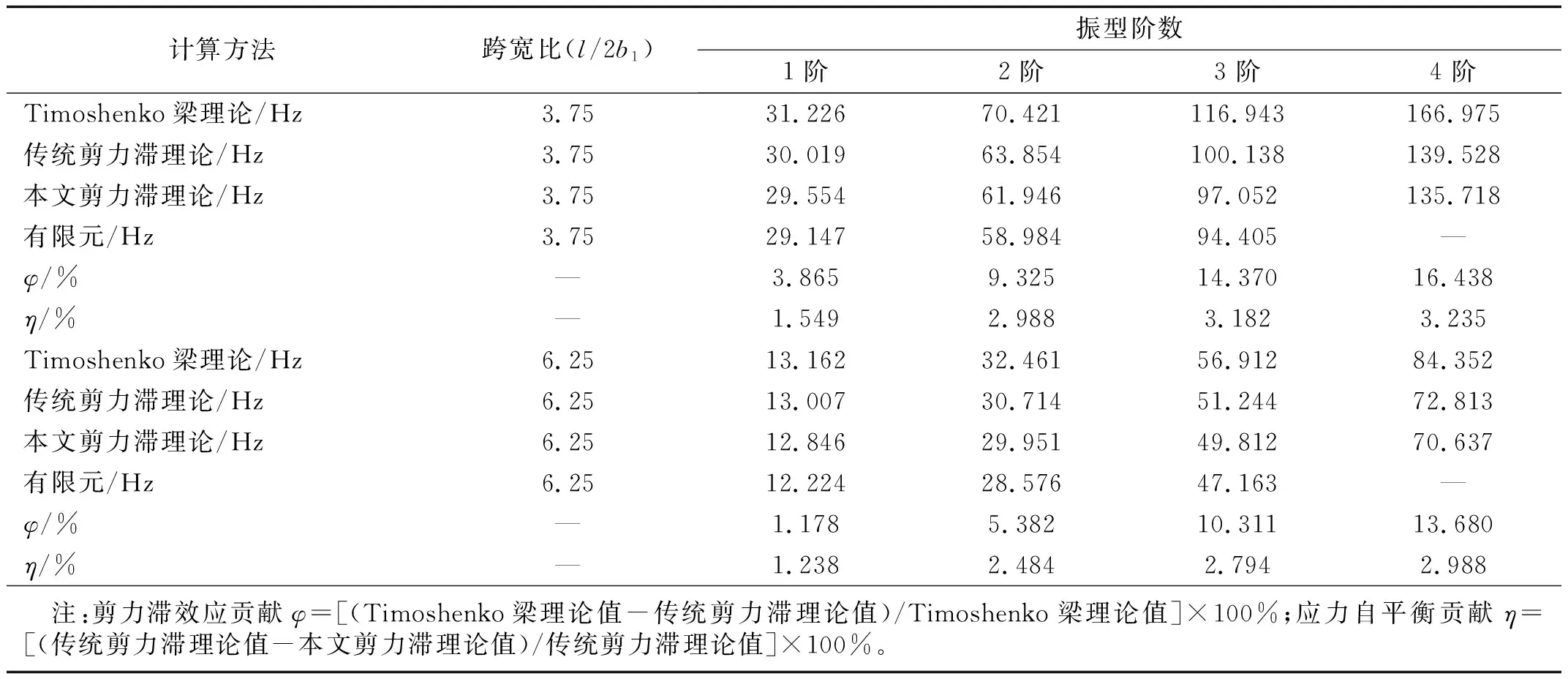
根据本文推导公式和其他算法可计算出不同边界条件下组合工字梁的自振频率值，计算结果如表1和表2所示，相应剪力滞效应和应力自平衡贡献分布如图4和图5所示。

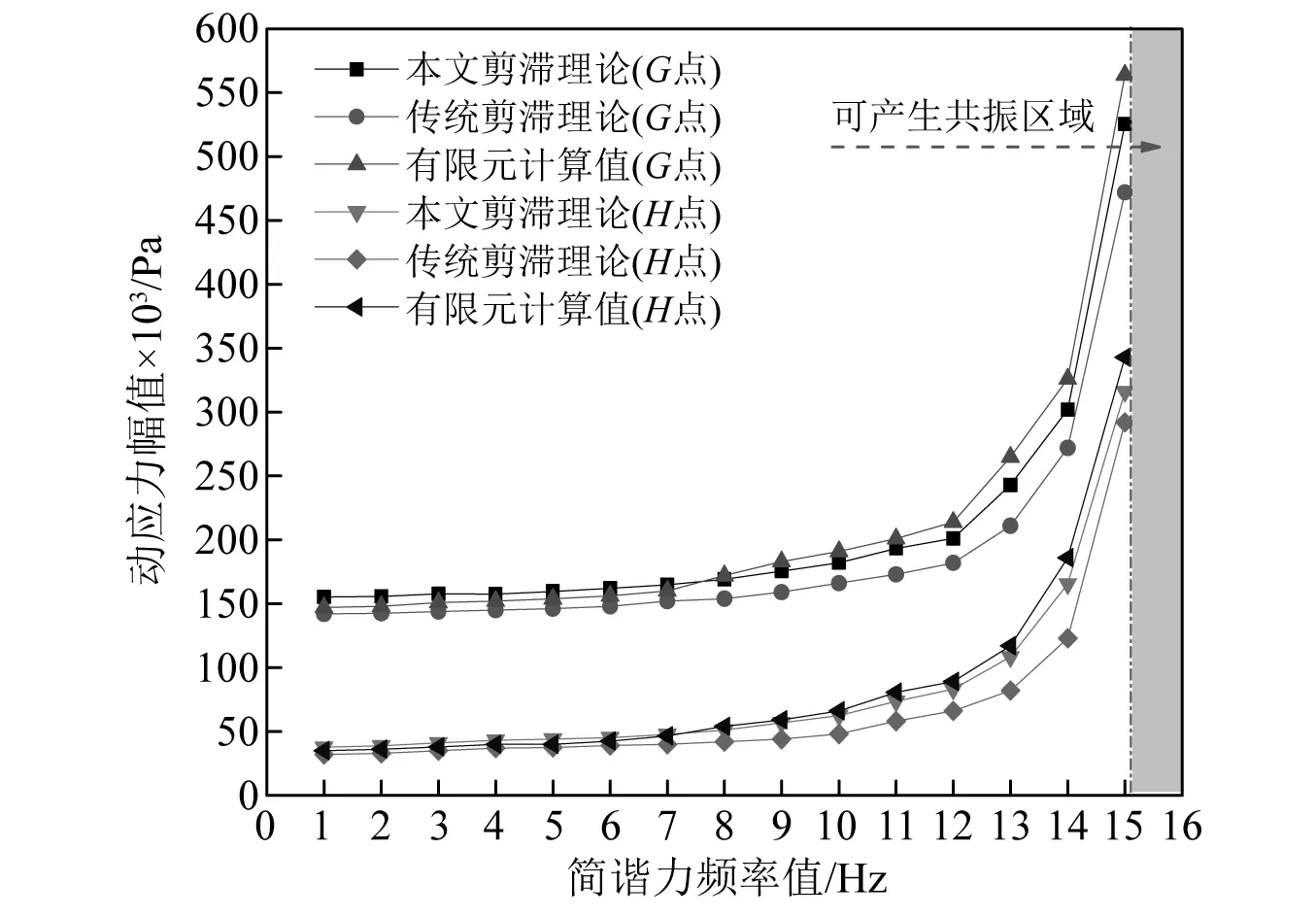
从表1、表2、图4和图5可以看出，本文理论计算所得组合工字梁弯曲自振频率值与有限元计算结果吻合良好，验证了本文方法的准确性，受剪力滞效应的影响，组合工字梁的各阶固有频率值普遍减小，随着频率阶数的增加，剪力滞后效应的影响逐渐增大；与简支组合梁相比，两端固支组合梁的频率值受剪力滞效应的影响更大，如l/2b1=3.75时，两端固支梁第4阶频率的剪力滞效应贡献达到16.438%；当组合梁跨宽比增大时，剪力滞后效应的影响随之减小。翘曲应力自平衡对组合梁自振频率的影响规律与剪力滞效应类似，但应力自平衡贡献值普遍小于5%。分析可知，当跨宽比一定时，本文剪力滞理论所得结构自振频率值<传统剪滞理论

表1 简支组合工字梁的自振频率Tab.1 Natural frequency of simply supported composite I-beam

表2 两端固支组合工字梁的自振频率Tab.2 Natural frequency of composite I-beam with fixed supports at both ends

图4 剪力滞效应贡献分布图Fig.4 Distribution diagram of contribution of shear lag effect

图5 应力自平衡贡献分布图Fig.5 Distribution diagram of balanced contribution of stress self leveling

组合工字梁跨中截面上G点和H点的坐标位置如图6所示，将式(28)～式(31)或其求导式代入式(32)、式(33)和式(34)后可以得相应边界条件下组合工字梁的强迫振动方程，结合MATLAB编写计算程序求得(l/2b1=3.75)组合工字梁跨中截面两点(G点、H点)的动应力幅值如图7和图8所示。

从图7和图8可以看出，在强迫振动分析中，剪力滞效应对组合工字梁翼板动应力幅值的影响很大，当简谐集中力频率相同时，G点的动应力幅值明显大于H点，即结构跨中横截面上各点的动应力幅值呈不均匀分布，剪力滞后现象明显，因而动力分析时组合工字梁的平截面假定不再适用；与传统剪滞理论相比，本文理论明显提高了翼板动应力幅值的计算精度，如算例中简支组合梁跨中作用简谐集中力频率为15 Hz时，G点和H点动应力幅值分别增大了9.21%和6.14%；两端固支组合梁跨中作用简谐集中力频率为28 Hz时，G点和H点动应力幅值分别增大了10.13%和7.06%。虽然由传统理论计算所得组合工字梁的基频值与本文理论值相差较小，但G点和H点的动应力幅值相差很大，因而在进行波形钢腹板组合工字梁强迫振动分析时翘曲应力自平衡是不可忽略的。

图6 G点和H点的坐标位置Fig.6 Coordinate position of G and H points

图7 简支组合梁G点和H点的动应力幅值Fig.7 Dynamic stress amplitudes at G and H points of simply supported composite beam

图8 两端固支组合梁G点和H点的动应力幅值Fig.8 Dynamic stress amplitudes at G and H points of composite beams with fixed ends

3 结 论

(1)以能量变分法和Hamilton原理为基础，提出一种能准确分析波形钢腹板组合工字梁弯曲振动特性的解析法，计算结果与ANSYS有限元计算值吻合良好，且计算精度明显提高，因而本文方法具有一定的理论意义和工程实用价值。

(2) 忽略剪力滞效应影响时，计算所得组合工字梁各阶频率值普遍较大，说明剪力滞效应降低了组合梁竖向刚度，随着频率阶数升高，剪力滞效应的影响增大；与简支组合梁相比，两端固支组合梁的频率值受剪力滞效应的影响更大，当组合梁跨宽比增大时，剪力滞后效应的影响随之减小。

(3)组合工字梁跨中横截面上各点的动应力幅值受剪力滞效应的影响较大，动力分析时平截面假定不再适用，虽然翘曲应力自平衡对结构自振频率的贡献值小于5%，但对翼板动应力幅值的影响最大可达10%以上，因而在进行组合工字梁动力反应分析时不可忽略翘曲应力自平衡的影响。