分数阶Brusselator振子的簇发振动与分岔
王艳丽, 李向红,,3, 王 敏, 申永军,3
(1.石家庄铁道大学 机械工程学院,石家庄 050043;2. 石家庄铁道大学 数理系,石家庄 050043;3.石家庄铁道大学 交通工程结构力学行为与系统安全国家重点实验室,石家庄 050043)
多尺度耦合现象已经广泛存在于机械、化工、生物等各个领域,成为目前非线性动力学领域的研究热点和前沿课题之一,其中簇发振动[1]是多尺度耦合系统的典型动力学行为,表现为在一个周期内系统交替出现沉寂态和激发态。文献[2-4]基于多尺度效应和非线性动力学稳定性与分岔理论,深入研究了神经系统中神经元放电活动的分岔模式。文献[5-6]在非光滑系统、周期激励系统、化学反应振荡系统的多尺度耦合效应方面做了大量的工作,比如利用微分包含理论深入研究了非光滑系统尺度效应的分岔机制,提出了转换相图和包络分析等方法,揭示了慢变激励下的簇发振荡模式及其演化过程。此外,国外很多学者也对簇发振动行为做了一些研究。Kouayep等[7]研究了一种光电振子,在电路中引入Colpitts振子会产生高频电信号,并表现出周期性和簇发性等动力学行为。Herve等[8]研究了单摆臂和双摆臂通过磁场耦合到非线性电路振动台上的响应,结果表明由于电子信号的传递,摆臂的位移会发生簇发振动,并且振动的形状周期和振幅取决于各种控制参数。然而,目前的研究主要集中在整数阶系统上,相比较下,分数阶系统的快慢效应研究成果较少。
近年来,分数阶微积分系统被广泛的应用到高能物理、反常扩散、复杂黏弹性材料力学本构关系、系统控制等若干领域[9],其理论研究和应用研究受到了国内外学者的广泛关注。比如,王军等[10-12]研究了一些含有分数阶微分的非线性与线性振子,采用平均法得到了系统的一阶近似解,证明了分数阶微分项不仅起着阻尼的作用同时还起着刚度的作用。Xu等[13]提出了具有多个时变时滞环节的分数阶竞争神经网络,并研究了这类神经网络的全局渐近稳定性,为揭示稳定性判据与网络拓扑结构之间的密切关系提供了一个新视角。Kandasamy等[14]研究了分数阶脉冲四元数值神经网络的多重Mittag-Leffler稳定性问题并仿真验证了所得到的主要结果的有效性。Sekerci[15]研究了不同分数阶定义下的食饵-捕食者系统的区别与联系。Sllva等[16]研究了两个基于分数阶微积分提出的常微分方程系统,解决了肿瘤细胞和免疫系统之间的动力学问题。
Brusselator模型[17]是一类描述自催化反应的典型振子,早在1968年由Prigogine等提出。由于催化剂的存在,使反应过程中不同反应物的反应速率存在较大的差别,即涉及快慢不同的时间尺度。在之后的几十年里,越来越多的学者投入到对Brusselator振子分岔、混沌以及近似解的研究中[18-24]。Rech[25]研究了周期强迫的四参数Brusselator振子,利用四维参数空间的一个给定截面,证明了该系统存在多稳态。Capone等[26]研究了全局Brusselator振子解的有界性,分析了离散化对线性稳定性的影响,发现在常微分方程系统中的稳定性与有扰动下的稳定性截然不同,并进行了非线性稳定性分析。Wang等[27]在研究分数阶微分系统的同步现象时首次提出了分数阶Brusselator系统,发现当分数阶阶次总和小于0.97时,分数阶Brusselator振子存在一个极限环。Jena等[28]采用分数阶约化差分变换法求解分数阶Brusselator振子的近似解,并对其进行了误差分析,发现该方法能够以级数形式快速收敛。目前围绕Brusselator振子整数阶成果较多,相比之下,其关于多尺度耦合的分数阶系统方面的研究尚在逐步发展阶段。
本文主要考虑外部周期扰动因素影响反应过程中催化剂浓度的情形下,分数阶Brusselator振子的簇发行为及其分岔机制,研究不同参数对系统的影响规律,为实际工程领域提供理论指导。
1 数学模型及分岔分析
分数阶Brusselator振子
(1)

(2)
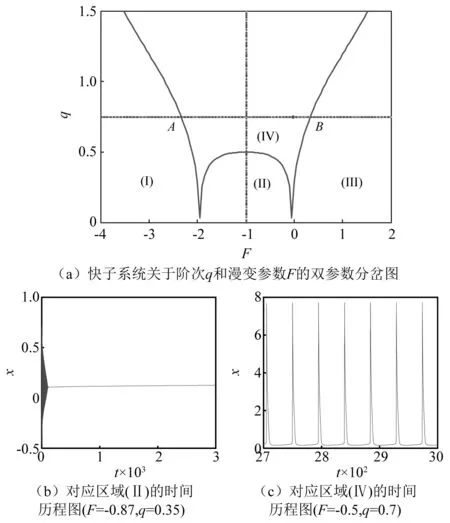
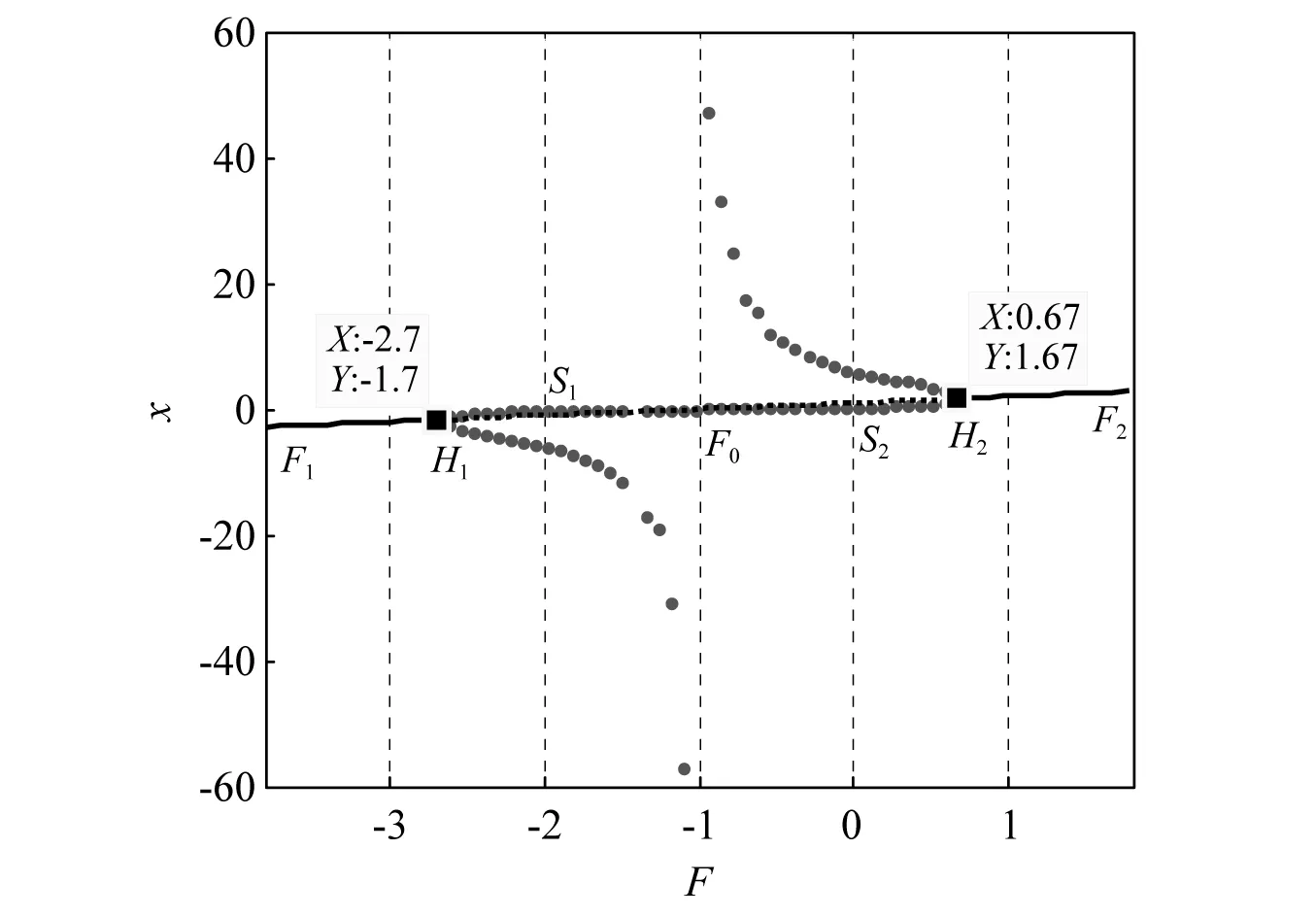
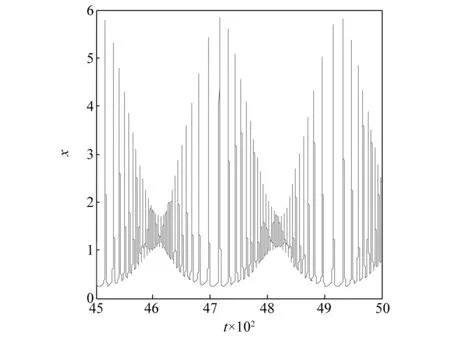
式中:n-1 实际上,催化过程易受到外界因素干扰及影响,因此要考虑外在周期因素。本文从外部扰动影响反应过程中催化剂浓度的情形出发,将这种扰动因素近似为外部周期扰动,从而进行动力学分析,其模型为 (3) 式中:γ和ω分别为外部周期扰动的幅值和频率,令θ=ωt,则式(3)可转化为广义自治系统 (4) 当ω远小于原系统的固有频率,式(3)会存在量级上差异的两个时间尺度,使其非线性行为更为复杂。此时由于周期性扰动,该反应会变为快慢两个时间尺度耦合的系统,在式(4)中变量x和y为快子系统,θ为慢子系统。基于快慢分析法,将慢变量视为快子系统的分岔参数。令F=γcosθ为快子系统的慢变参数,则快子系统表示为 (5) 由 (6) 得到快子系统式(5)的平衡点 下面将按照A+F是否等于0分两种情况进行讨论。 平衡点E0处的特征方程为 λ2+[(A+F)2+1-B]λ+(A+F)2=0 (7) 式(5)在平衡点E0处的Jacobian矩阵为 (8) 进一步分析分数阶系统发生Hopf分岔的条件,选取系统参数F为分岔参数,定义函数 根据整数阶系统发生Hopf分岔的条件,进而推广到分数阶系统发生Hopf分岔[29]的条件,见命题1。 命题1当B≥1,且 若满足下列条件: 条件1式(5)对应的特征方程有一对复共轭根λ1,2(F)=θ(F)±iω(F); 下面证明此命题: λ1,2=θ(F)±iω(F) (9) 条件1得证。 (2) 在命题所给条件下,特征方程仅有一对共轭复根,那么有 因此, (11) 基于分数阶微分方程稳定性理论[30],可得式(5)失稳的边界条件 (12) 具体表达式为 (13) 条件2得证。 (3) 由于 (15) 两边关于F求导,可得 其中, θ(F)=[B-1-(A+F)2]/2, θ′(F)=-(A+F), (17) 因为A+F≠0,所以 θ′(F*)ω(F*)-ω′(F*)θ(F*)= (18) 条件3得证。综上,命题1成立。 选取参数A=1,B=3.8,可得到快子系统的阶次q和慢变参数F之间的双参数分岔图。如图1(a)所示,区域(I)、区域(II)和区域(III)内平衡点是稳定的,当跨越临界线进入区域(IV)时,平衡点失稳同时出现稳定的极限环,图1(b)和图1(c)分别给出了区域(II)和区域(IV)中的系统时间历程图。图1(a)中A和B表示q=0.75时对应的两个临界点。可见,式(5)有两个Hopf分岔点,并且随着分数阶阶次的减小,两个Hopf分岔点之间的距离越来越小。 当q=1时,图2给出了快子系统式(5)关于慢变参数F的分岔图,其中平衡线F1-F2有五种类型的平衡点,分别是位于F1-H1上的稳定焦点,H1-S1上的不稳定焦点,S1-F0,F0-S2上为不稳定结点(这里不包括F0点,即F=-1的情况),S2-H2上的不稳定焦点,H2-F2上的稳定焦点。其中H1和H2为Hopf分岔临界点,参数值为FH1=-2.67,FH2=0.67,当F在H1-F0和F0-H2(这里不包括F0点的情况)快子系统存在稳定的极限环,图3给出了F为-1.5和-0.5时的相图。 图1 系统的分岔图和时间历程图Fig.1 Bifurcation diagram and time history diagram of the system 图2 快子系统的平衡点关于慢变参数F的分岔图Fig.2 The bifurcation diagram with respect to parameter F 图3 极限环的相图Fig.3 The phase diagram of limit cycle 对于整数阶的情形,若A+F=0,此时F=-1。对于式(5),直线x=0上任何点均为系统的奇点,即F=-1时,纵坐标y轴是奇线。显然,式(5)的平衡点为(0,m),m为任意实数。在(0,m)处对系统线性化可得矩阵 (19) 特征值是0和-4.8,此时不能直接判别平衡点的稳定性,需要借助中心流形定理进行判断。构造一个T矩阵,其列为M的特征向量,即 (20) 此时,显然不是标准形,因此需进一步标准化来判断其平衡点的稳定性,故有 (21) 应用变量代换 (22) 可得 (23) 在所给参数条件下整数阶Brusselator式(5)可变为 (24) 将式(23)代入式(24)中可以进一步推出 (25) 此时, Ec={(x1,x2)∈R2x2=0},x轴 (26a) Es={(x1,x2)∈R2x1=0},y轴 (26b) 从而可知式(25)是标准形式,因此 (27) (28) 中心流形方程为 h′(x1){-18.24[h(x1)]3-4.8x1[h(x1)]2}+ 18.24[h(x1)]3+4.8x1[h(x1)]2+4.8[h(x1)]=0 (29) 图4 奇线Fig.4 Singular line 对于F=-1时,分数阶的稳定性情况,可以利用数值模拟进行验证。图5是对应分数阶情况下,F=-1时的时间历程图。可以发现,对于分数阶系统,与整数阶系统有相同的结论,即在F=-1处,分数阶系统也存在稳定的奇线x=0。 图5 当F=-1时的时间历程图Fig.5 The time history for F=-1 本部分研究系统簇发振动行为与机理,以及不同参数对簇发振动的影响。 图6是参数γ=0.8,ω=0.03,q=1时的时间历程图。可以计算出,整个周期振动频率恰好是外部周期扰动频率0.03。为了进一步揭示其簇发振动的产生机理,给出了关于变量x与慢过程F=0.8cos(0.03t)的转换相图,并将其转换相图和分岔图叠加得到图7。 图7进一步表明了簇发振动的产生机理。假设在一个周期的演变过程中,相轨迹从A点出发,在A点时平衡点是不稳定的,并受到快子系统稳定极限环的吸引,导致系统呈现出大幅度振动而处于激发态。极限环会在经过Hopf分叉点H2后消失,只有稳定的平衡点吸引子,系统的大幅振动将逐渐收敛至稳定平衡线,此时系统完成了激发态演变到沉寂态的过程。最后当轨线到达B时,慢变过程F=0.8cos(0.03t)达到最大值,轨线将按照F减小的方向运动。此时系统仍处于沉寂态,并且在经过分岔点H2,系统并不会立刻进入激发态,而是由于分岔延迟在点P,开始大幅振动,系统再次处于激发态,直至完成了一个周期的运动,该簇发属于Hopf簇发。同时,图8(a)和图8(b)分别给出了周期激励增加和减少两个方向上激发态滞后现象。 图6 当q=1时的时间历程图Fig.6 The time history for q=1 图7 当q=1时,转换相图和分岔图的叠加Fig.7 Overlapping of transition portrait with bifurcation diagram for q=1 图8 当q=1时,簇发现象的产生机理Fig.8 The generation mechanism of the periodic bursting oscillation for q=1 下面讨论分数阶阶次对簇发振动的影响,固定参数γ=0.8,ω=0.03。图9和图10分别给出了q=0.75和q=1.15时的时间历程图。 图9 当q=0.75时的时间历程图Fig.9 The time history for q=0.75 图10 当q=1.15时的时间历程图Fig.10 The time history for q=1.15 通过对比图9、图6和图10可以看出,系统的激发态持续时间会随着分数阶阶次的增大而变长,相对应沉寂态时间会缩短。该结论也可通过图1(a)中快子系统的临界阶次和慢变参数之间的关系图得到,即阶次越小,两个Hopf分岔点之间的距离越小,从而导致激发态的持续时间变短。同时,系统幅值也会随着分数阶阶次减小而降低。 为了研究周期扰动幅值对簇发振动的影响,固定q=0.75,ω=0.03,通过改变γ的值来具体研究幅值的影响。由图1(a)可知,当q=0.75时,两个Hopf分岔点A,B的参数值分别为FA=-2.33,FB=0.33,这说明,当FA 当扰动幅值γ>2.33,F的变化范围包含[-2.33,0.33],存在三种吸引子:位于中间的稳定极限环和位于两边的稳定焦点吸引子,这将导致系统的轨迹产生变化。其中,中间与左右两端的吸引子的双稳性导致系统轨线在激发态与沉寂态之间相互转迁,这样会出现两种激发态和两种沉寂态的双Hopf簇发现象,图11给出了当γ=2.5时的时间历程图。 图11 当γ=2.5时的时间历程图Fig.11 The time history for γ=2.5 如果扰动幅值0.33<γ<2.33,整个系统只涉及快子系统的两种吸引子,即右侧的稳定焦点吸引子和中间的极限环吸引子。此时,系统只存在单侧双稳性。如图9所示,为单Hopf簇发。 如果扰动幅值γ<0.33,此时系统轨线只涉及到稳定极限环吸引子,双稳性演变为单稳性,沉寂态消失,两个激发态连接在一起,图12给出了此种情况γ=0.3时的时间历程图。 图12 当γ=0.3时的时间历程图Fig.12 The time history for γ=0.3 由此可见,在快慢耦合的系统中,如果周期扰动因素为慢变过程,则扰动幅值的大小可以调节系统的振动模式,其机理是涉及系统吸引子的种类发生了改变。 本文研究了具有外部周期扰动的分数阶Brusselator振子,当外部周期扰动频率远小于系统固有频率时,系统涉及两个不同的时间尺度,表现出明显的快慢效应,存在典型的簇发振动。通过系统的稳定性分析发现,系统存在一条稳定的奇线,并利用中心流形定理和数值模拟证明了其稳定性。在非奇线处,根据分数阶系统稳定性理论讨论了系统的稳定性,并给出了发生Hopf分岔的充分条件。 分数阶阶次和幅值对簇发振动具有明显的影响。随着分数阶阶次的减小,激发态逐渐减弱,其原因是由于随着参数变化,两个Hopf分岔点之间的距离变小,导致系统处于激发态的时间缩短。当扰动幅值较大时,系统存在双Hopf周期簇发振动现象,其产生机理是系统涉及快子系统的两个Hopf分岔,导致了激发态与沉寂态之间相互转迁的分岔行为;随着扰动幅值的减小,双Hopf簇发逐渐演变为单Hopf簇发;当幅值继续减小时,系统不再涉及Hopf分岔点,且仅涉及稳定极限环吸引子,单稳性会使系统一直处于激发态,沉寂态消失,但是整个周期振动是两个频率的耦合。 以上结论为研究分数阶Brusselator振子的振动与控制提供了重要的理论依据和技术服务,同时整数阶与分数阶系统行为的本质差异问题需要进一步深入研究。1.1 情况一:A+F≠0





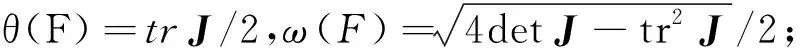



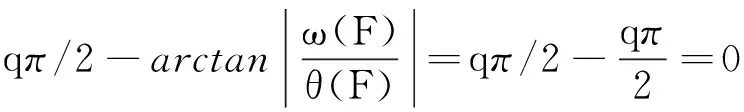

1.2 情况二:A+F=0
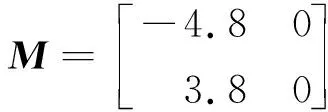
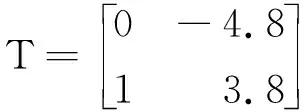

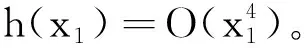



2 簇发振动行为及参数的影响
2.1 簇发振动及其机理



2.2 分数阶阶次对簇发振动的影响


2.3 周期扰动幅值对簇发振动的影响

3 结 论

