基于改进多重同步挤压广义S变换的结构瞬时频率识别研究

袁平平， 程雪莉， 王航航， 沈中祥， 任伟新， 张 健

(1. 江苏科技大学 材料科学与工程学院，江苏 镇江 212100； 2. 江苏新扬子造船有限公司，江苏 靖江 214532； 3. 江苏科技大学 土木工程与建筑学院，江苏 镇江 212100； 4. 江苏科技大学 船舶与海洋工程学院，江苏 镇江 212100；5. 深圳大学 土木与交通工程学院，广东 深圳 518061)

随着社会的发展，土木工程逐渐趋于大型化、高层化、结构异形化，其在人们日常生活中扮演的角色也愈发重要[1]。土木工程结构的损伤必定会导致其动力特性发生变化，随着损失的累积其一旦出现问题，轻则发生财产损失、影响人们的正常生活，重则造成人员伤亡[2-3]。Kijewski等[4]认为工程结构具有较长的周期运动，动力特性在其使用寿命内往往会随着时间的推移而发生变化。因此，精确识别工程结构的瞬时频率等时变动态参数至关重要，这将有助于工程结构的状态监测、损伤识别及安全评估等。

时频分析作为一种新兴的信号处理方法，是研究非平稳信号的一个重要工具，其通过设计时间和频率的联合函数，把时域信号转换到二维平面上，从而在时间域和频率域上同时体现信号的能量和强度[5-6]。作为传统时频分析方法，短时傅里叶变换(short-time Fourier transform, STFT)、Wigner-Ville(Winger-Ville distribution, WWD)分布、S变换(S-transform, ST)、希尔伯特-黄变换(Hilbert-Huang Transform, HHT)等均存在一定的不足[7]。基于此，诸多学者进一步展开了相关研究。裴强等[8]研究了基于时频分析ST的高层框架损伤识别。Zidelmal等[9]提出了基于紧凑型支持内核的ST。续秀忠等[10]提出了一种基于线性时频表示和Hilbert变换的时变模态参数识别方法。Hou等[11]提出了一种基于连续小波的时变结构瞬时模态参数识别。连续小波变换与傅里叶变换相似，能够实现信号变换与信号重构，且能保持原有信息的完整并具有可逆性。Daubechies等[12]提出了同步挤压小波变换(synchrosqueezed wavelet transform, SST)，该方法以小波变换为基础，通过对时频周围的能量进行挤压，有效提高了时频能量的集中度。张志禹等[13]将SST应用于地震信号瞬时属性的提取。刘景良等[14-15]提出了基于SST的结构瞬时频率识别并对其进行了改进。受同步挤压变换算法的启示，以实现理想的时频分析为目标，Yu等[16]提出了一种新的时频分析方法，即同步提取变换(synchroextracting transform, SET)。该方法是基于STFT的一种时频分析方法，可提高瞬时频率的识别精度。康佳星[17]研究了SET在地震信号分析中的应用。张文海等[18]提出了基于SET与Vold-Kalman滤波的燃机阶次跟踪方法。Li等[19]提出了用于地震时频分析的时间同步提取广义Chirplet变换。然而，SET无法实现信号的精确重构，因此，Yu等[20]进一步提出了多重同步压缩变换(multi-synchrosqueezing transform, MSST)，该方法对STFT获得的时频图执行多次同步压缩处理，从而有效提高了时频能量的聚集性。

本文对广义S变换(generalized S-transform,GST)的窗函数进行了改进，并根据能量集中度(concentration measure, CM)[21]选取窗函数的参数，同时结合MSST，提出了一种新颖的改进多重同步挤压广义S变换(improved multi-synchrosqueezing generalized S-transform, IMSSGST)。在数值模拟方面，采用两层剪切框架时变结构验证该方法的准确性；试验方面，采用某七层钢筋混凝土(reinforced concrete, RC)剪力墙振动台的试验数据进行了时频分析，用于验证该方法在实际工程中的实用性和准确性。

1 理论基础

1.1 改进广义ST

ST是STFT和连续小波变换(continue wavelet transform,CWT)相结合联合起来的一种时频分析方法，其特点是引入了宽度和频率成反比的高斯窗

(1)

式中：Sx(τ,f)为ST；x(t)为原始信号；g(t)为窗函数；τ为时移因子；f为频率。g(t)的表达式为

(2)

将式(2)代入式(1)，可以得到ST的表达式，即

(3)

ST具有完全可逆性，其逆变换如式(4)所示

(4)

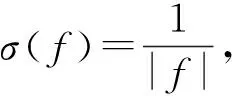
(5)

将式(5)代入式(1)即可得到GST，其计算结果为

(6)

(7)

该窗函数可以通过多项式来表达GST中的窗函数。将式(7)代入式(1)得到IGST(improred GST)的计算结果如式(8)所示

(8)

IGST的频域表达式如式(9)所示

(9)

1.2 IGST的参数优化算法

本文采用能量CM的方法进行计算

(10)

对IGST进行归一化处理，可得

(11)

则，IGST的优化问题可由式(12)表示

(12)

优化问题的约束条件与所分析窗口的宽度范围有关，窗口不应太窄而改变时间分辨率，但也不能太宽而影响频率分辨率，即

(13)

式中：Ts为采样周期；f∈[fmin,fmax]；fmin=1 Hz；为满足奈奎斯特采样定理，fmax取采样频率的一半。式(13)可简化为

(14)

在Zidelmal等和He等的研究中，相关学者令m∈(0,3]，p∈[0,3]，r=[0,1]，K=10，L=1 000。本文采用相同的边界条件，因此，最终的优化问题如下所示

(15)

通过优化算法对上述问题进行求解即可得到IGST窗函数的参数值。

1.3 改进多重同步挤压广义S变换

原信号的瞬时频率ωi(τ,f)可由式(16)得到

(16)

其中，

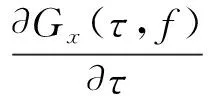
(17)

所以，对信号x(t)的IGST计算结果Gx(τ,f)进行单次压缩，可得

(18)

进行多次挤压，可得IMSSGST的计算结果如式(19)所示

…

(19)

其中，

(20)

2 数值模拟

2.1 框架结构模型

实际工程结构往往受到极限荷载或周期荷载的作用，结构的刚度也会随之发生改变，其响应信号的瞬时频率往往也会随之改变。为了验证该方法对结构瞬时频率识别的可行性，建立两层框架模型进行验证，如图1所示。该结构的刚度会随着时间变化，结构的具体参数如表1所示。

图1 两层剪切框架结构Fig.1 Two-layer shear frame structure

表1 两层剪切框架结构模型参数

框架结构相应的运动方程

(21)

结构的刚度按式(22)和式(23)变化，其时变刚度如图2所示。

(22)

(23)

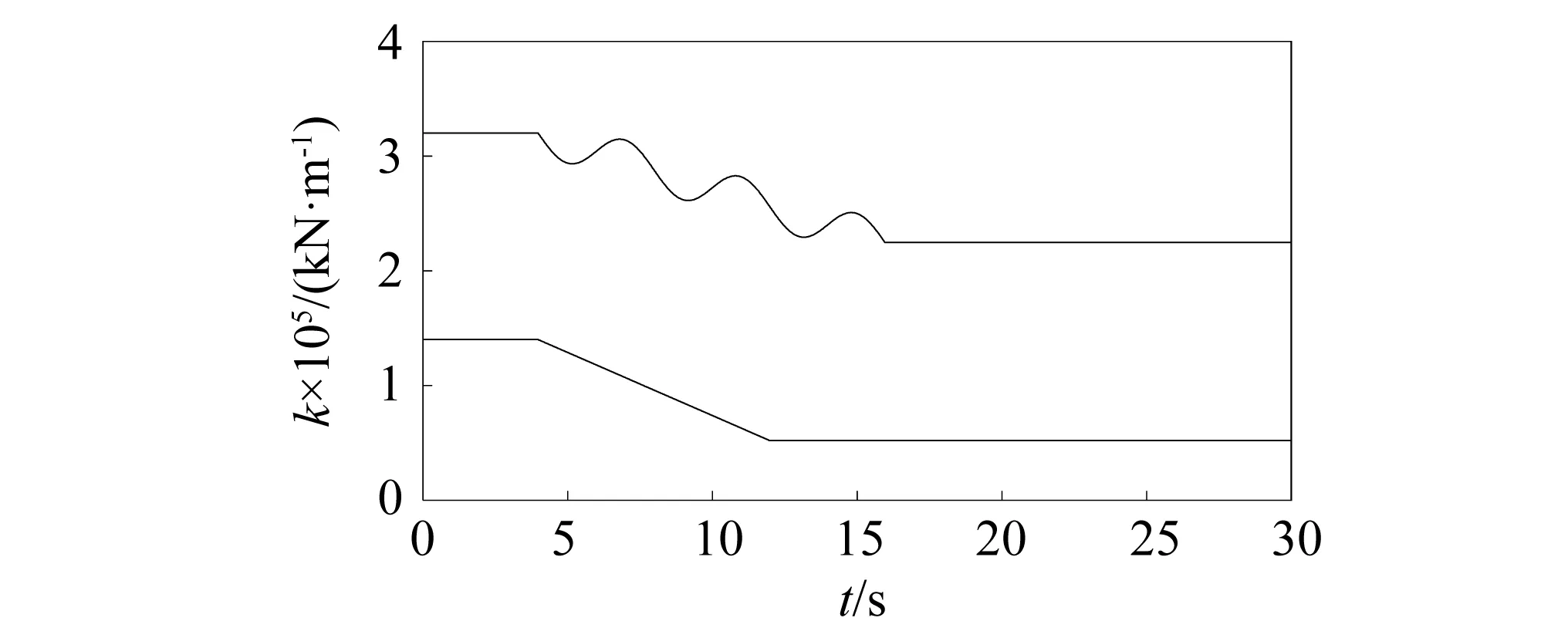
图2 框架结构刚度Fig.2 Stiffness of frame structure

通过矩阵特征值计算，可得框架结构的理论瞬时频率如图3所示。

2.2 瞬时频率识别

对该框架结构进行白噪声激励，用Runge-Kutta法求得结构的位移，速度及加速度响应。采样频率为50 Hz，采样时间为30 s。其中：噪声激励如图4所示；第一层结构加速度响应见如图5所示。

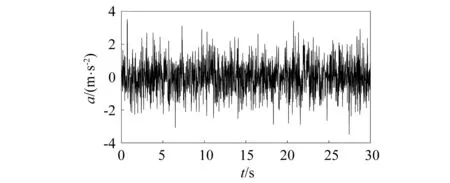
图4 白噪声激励Fig.4 White noise excitation

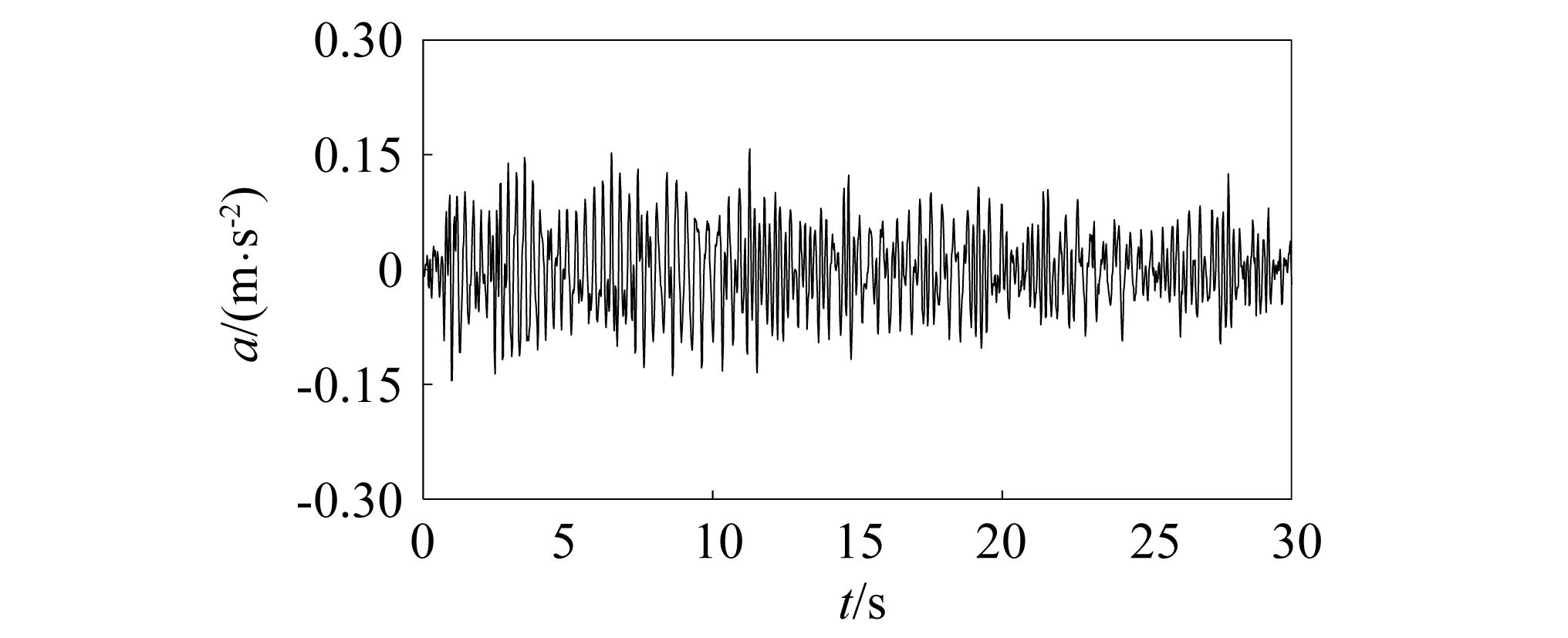
图5 白噪声激励下第一层的加速度响应Fig.5 Acceleration response of first layer under white noise

为了确定IMSSGST的压缩次数，本文采用瞬时频率在整个时间历程内的均方根值作为瞬时频率识别精度的指标(index of accuracy，IA)。IA值越小，说明识别值与理论值越接近。随着压缩次数的增加，IA值会趋于平稳，以此来确定IMSSGST的压缩次数。IA值的计算方法如下所示

(24)

式中：fd(t)为瞬时频率识别值；fe(t)为瞬时频率理论值。

MSST和IMSSGST识别的低频的精度值基本保持一致，但在高频处，IA值在第4次和第5次达到最小，识别的精度最高，如图6所示。本文将采用一次、两次和四次压缩分别对信号进行频率识别。

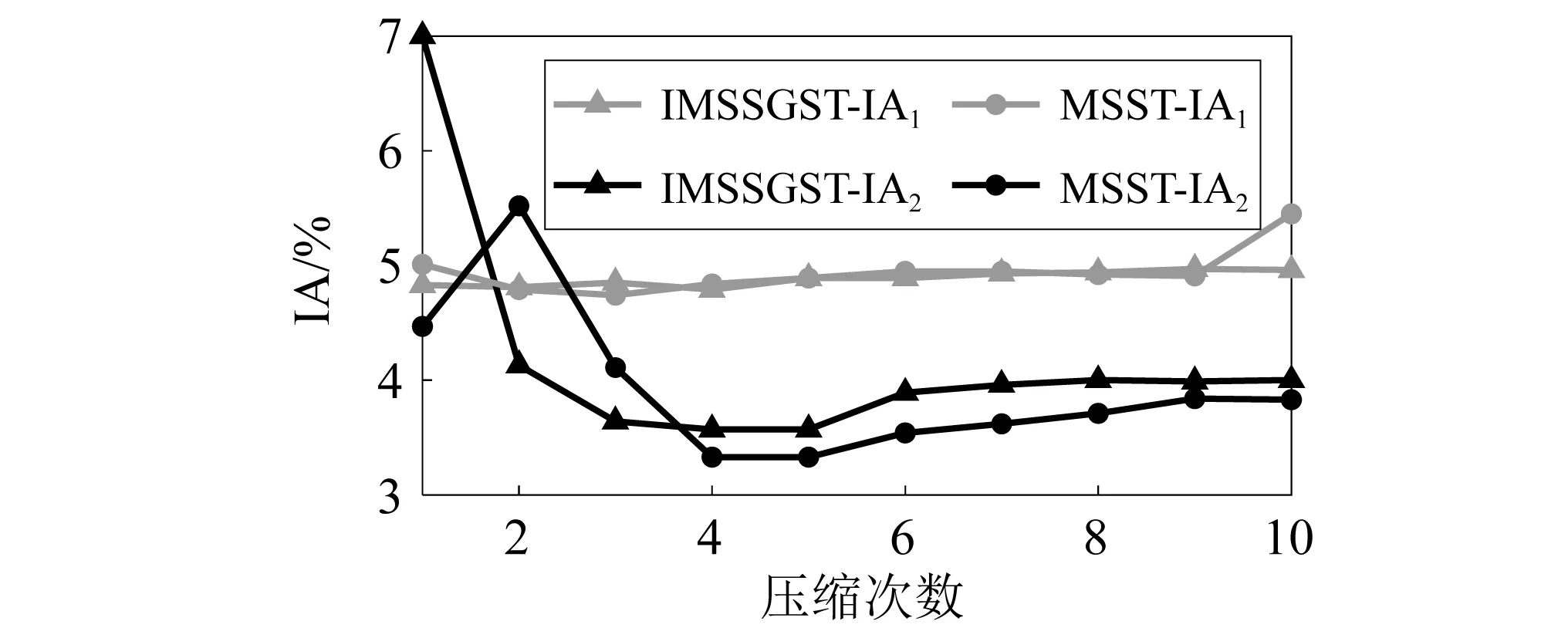
图6 压缩1～10次的IA值Fig.6 IA value compressed 1-10 times

对加速度响应信号进行IMSSGST及MSST时频分析，压缩次数为一次、两次和四次，其中，通过优化算法得到IMSSGST的参数：m=3，p=2.155 1，r=0.645 4。时频分析结果如图7所示。从图7可知，随着压缩次数的增加，IMSSGST、MSST的时频能量更加集中。

提取四次压缩后的频率如图8所示。从图8可知，通过多次压缩后，IMSSGST和MSST均能有效识别该框架结构的瞬时频率，且识别值与理论值保持在较小的误差范围内，有较高的实用性。

图7 时频分析结果Fig.7 Time frequency analysis results

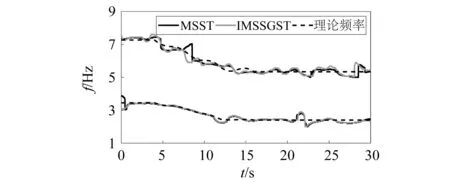
图8 瞬时频率识别结果Fig.8 Instantaneous frequency identification results

3 试验验证

为了验证IMSSGST对实际工程结构瞬时频率的识别效果，本文对加州大学圣地亚哥分校Panagiotou等[24]设计完成的七层RC剪力墙振动台的试验数据进行了时频分析。施加于结构的地震波加速度及剪力墙的加速度响应，分别如图9和图10所示。

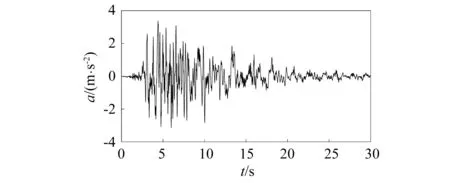
图9 施加在剪力墙的地震波Fig.9 Seismic wave applied to the shear wall

图10 剪力墙的加速度响应Fig.10 Acceleration response of shear wall

分别用IMSSGST、MSST对测得的加速度响应信号进行时频分析，压缩次数为一次、两次和四次，时频分析结果如图10所示。在IMSSGST中，通过优化算法得到m=1.346 9，p=3，r=0.917 0。由图11可知：随着压缩次数的增加，IMSSGST、MSST识别出的频率脊线也更加准确、明显；在相同压缩次数下，与MSST相比，IMSSGST的曲线波动更小，这有利于提取结构的瞬时频率。

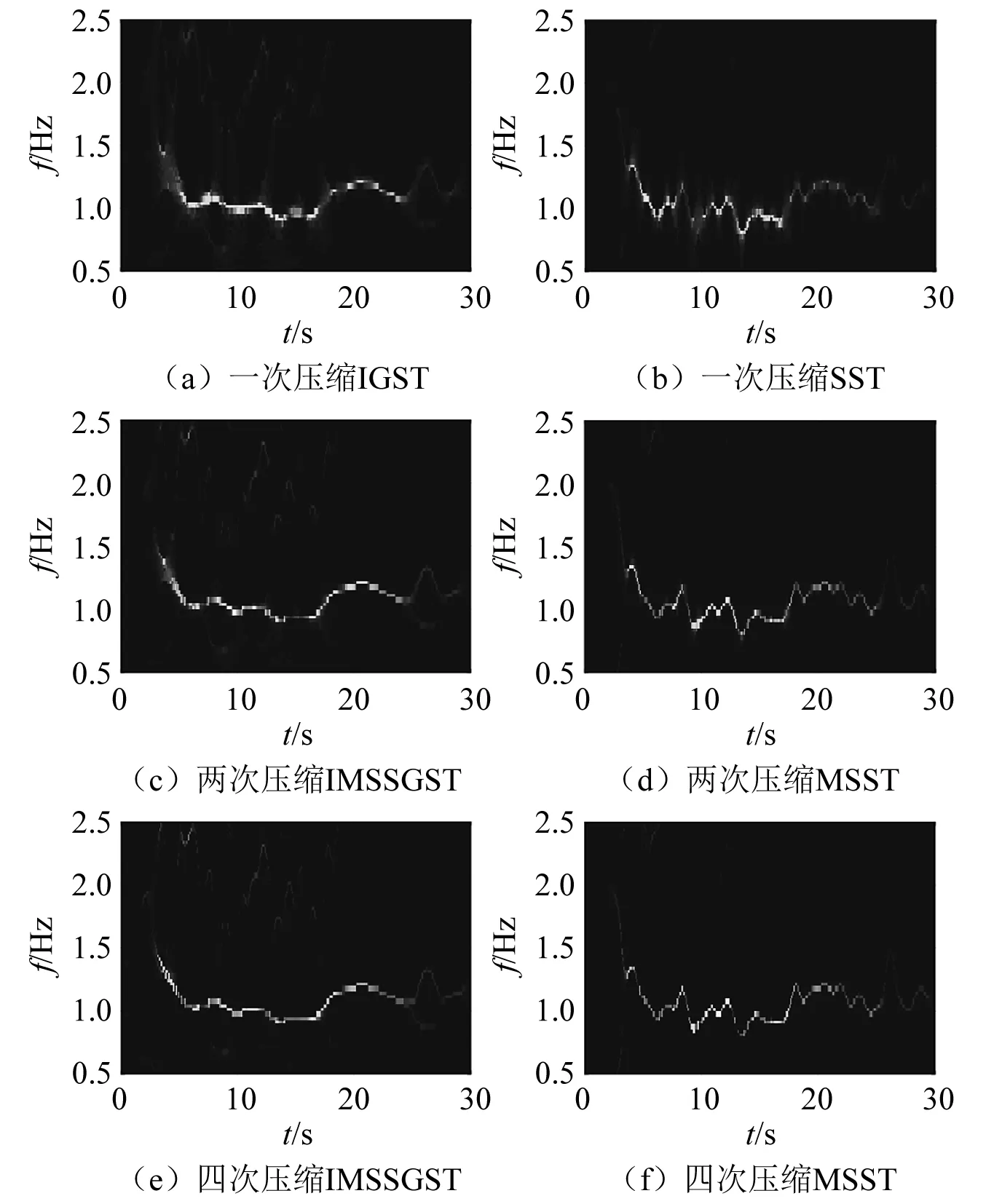
图11 剪力墙的多次压缩时频分析结果Fig.11 Time-frequency analysis results of shear wall

采用极值法提取IMSSGST、MSST四次压缩后的瞬时频率，频率提取结果如图12所示。从图12可知，该RC剪力墙结构在地震激励作用下的频率范围在0.8～2.1 Hz，IMSSGST和MSST都能有效地识别其频率范围，但是，IMSSGST识别的瞬时频率的曲线更加光滑，曲线波动更小。

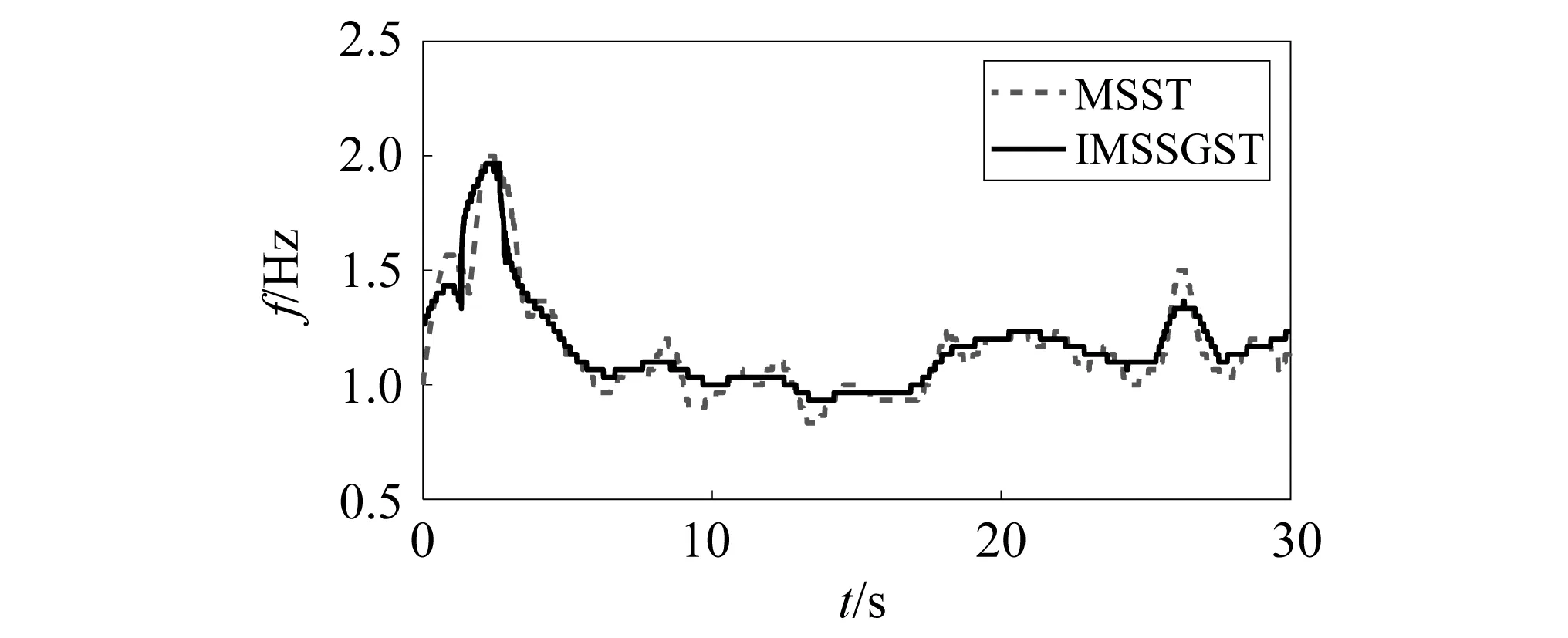
图12 四次压缩后剪力墙的频率识别结果Fig.12 Frequency identification result of shear wall after four-synchrosqueezing

4 结 论

本文结合IGST和MSST，提出了新颖的IMSSGST，并将其应用到工程结构的瞬时频率识别中。对两层剪切框架和七层RC剪力墙结构进行了瞬时频率识别，数值模拟和试验结果表明：

(1) 将CM原理和参数优化算法结合起来，可以快速得到IGST中调节因子的参数，有效地缩短了IGST的计算时间。

(2) 通过多次压缩后，IMSSGST识别的瞬时频率更加准确，能量更加集中，有效地改善了IMSSGST的频率识别效果。

(3) 与MSST算法相比，压缩相同次数的情况下，IMSSGST识别的频率曲线更加光滑，曲线波动更小，且与理论值更加接近，是一种准确、高效的时频分析方法。