基于6自由度振动试验台的轨道几何不平顺复现方法及应用研究
张 嘉, 邬平波, 刘潮涛, 宋 烨, 李凡松
(西南交通大学 牵引动力国家重点实验室,成都 610031)
列车运行过程中会受到各种外界激扰,如横风激扰、轨道不平顺激扰、弓网耦合振动等。为了研究外界激扰下车辆系统的振动特性,通常需要开展专项线路试验,但线路试验成本高,所受制约因素较多,且会给车辆正常运行带来安全隐患,因此国内外相关科研机构均考虑在试验台上复现列车实际运行时可能受到的各类外界载荷以测试分析车辆系统的动态响应,评估车辆系统相关性能。
国内外多家科研机构都建有自己的整车试验台,根据实现功能的不同可分为滚动试验台、振动试验台和滚动振动试验台。例如我国国内中车四方股份的整车滚动试验台,可模拟和复现整车在平直线路上的运行状态;中车长客股份建成的转向架参数测试试验台可模拟车辆偏载以及曲线通过等实际运行工况,以对单个转向架进行参数测试,张兰等[1]针对该试验台开展了复现轨道激励的相关研究;中车四方所建有整车振动试验台,张洪[2]在该振动台上通过输入轨道不平顺激励,测试了整备车体在多个速度等级下的振动响应,并对试验车体的模态参数进行辨识;牵引动力国家重点实验室的机车车辆滚动振动试验台[3-5]最高试验速度可达600 km/h,可根据试验需要施加各种类型的轨道激扰;在国外,例如美国铁路运输技术研究中心设有车体疲劳与振动试验台、加拿大地面交通技术中心、日本川崎重工等都建有自己的车体振动与疲劳强度试验台[6]。
理想中的铁路轨道是左右两条连续的、平直的且表面光滑的钢轨,但实际中由于钢轨的加工误差、安装误差以及使用过程中的磨耗等因素影响,导致轨道实际的几何形状以及空间位置都与理想中存在偏差,这种偏差称作是轨道不平顺,轨道不平顺作为车辆系统振动的最主要因素,有多种分类方法。可按照轨道对车辆激扰的方向分类,具体可分为垂向不平顺、横向不平顺和复合不平顺,即轨道几何不平顺;也可按照不平顺的波长特征或形状特征分类。
本文主要针对轨道几何不平顺,尤其包含线路扭曲不平顺在振动试验台上的复现方法进行了讨论,将齐次坐标变换的方法引入到试验台运动控制信号的解算中,并首次建立了振动试验台的动力学模型,验证了控制信号解算方法的正确性;利用在振动试验台上复现的实测轨道激励成功地对转向架构架进行了模态参数识别,为转向架模态测试提供了新方法。
1 轨道几何不平顺类型及6自由度振动试验台结构介绍
1.1 轨道几何不平顺类型
轨道几何不平顺按照方向可分为垂向不平顺和横向不平顺,如图1所示。轨道垂向不平顺常见的形式有高低不平顺与水平不平顺,轨道横向不平顺常见的形式有方向不平顺与轨距不平顺;此外,常见的轨道几何不平顺还包括线路扭曲不平顺。
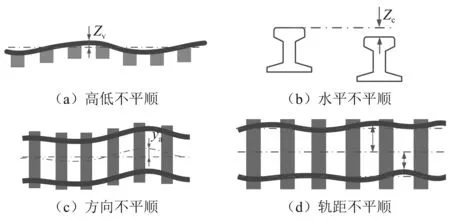
图1 轨道随机不平顺形式Fig.1 The form of rail random irregularities
(1) 轨道高低不平顺:如图1(a)所示,钢轨顶面沿着轨道长度方向高低不平,这通常是由钢轨表面不平、车辆通过钢轨时轨道产生弹性变形等因素引起的[7]。记线路名义中心线为一条水平直线,左、右侧钢轨与线路名义中心线之间的高度差分别为Z1,Zr,则基于轨道中心线描述的高低不平顺用Z1与Zr的平均值Zv表示,三者之间的计算关系如式(1)所示。轨道高低不平顺通常会使车辆产生点头或浮沉姿态,会对车辆的垂向振动产生影响。
(1)
(2) 轨道水平不平顺:如图1(b)所示,轨道水平不平顺是指同一横截面上,左右钢轨顶面对应点的高度差沿着轨道长度方向的波动变化。以左轨高于右轨为正,水平不平顺导致的轨道中心线的实际高度Zc可以用左右钢轨的高度差表示,如式(2)所示。轨道水平不平顺会导致车辆发生横移和侧滚振动。
Zc=Zl-Zr
(2)
(3) 轨道方向不平顺:如图1(c)所示,轨道方向不平顺通常是指左右钢轨内侧面与线路名义中心线之间的横向偏移。记左、右侧钢轨的横向偏移量分别为yl,yr,则基于轨道中心线的轨道方向不平顺用yl与yr的平均值ya表示,三者之间的计算关系如式(3)所示。轨道方向不平顺通常会使车辆产生摇头或侧滚运动,会影响车辆的横向动力学性能。
(3)
(4) 轨距不平顺:国内的标准轨距是1 435 mm,具体是指左右钢轨顶面向下16 mm处测量左右钢轨之间的横向内侧距。但通常左右钢轨对应点的横向跨距不是严格的1 435 mm,将实际轨距与名义轨距之间的偏差称作是轨距不平顺。记左、右侧钢轨与线路名义中心线之间的横向偏移量分别为yl,yr,以实际轨道向左轨偏移为正,则基于轨道中心线的轨距不平顺以实际轨距与名义轨距之差来表示,如式(4)所示。轨距不平顺会改变轮轨间接触几何关系,会显著地影响到车辆的横向动力学性能。
yg=yl-yr-g
(4)
式中,g为名义轨距。
(5) 线路扭曲不平顺:线路扭曲不平顺定义为在一定轨道长度范围内,左右两股钢轨间的水平差呈现“正负正”或“负正负”的状态[8],此时左右钢轨顶面相对于轨道平面出现扭曲,如图2所示。图2中:L/2为量测基长;A为不平顺波幅,线路扭曲不平顺的最大幅值表示为A-(-A)=2A。当扭曲不平顺的幅值过大时,会出现同一个转向架前后两条轮对处于三点支撑状态,会给行车安全带来极恶劣的影响,因此对于实际线路上的扭曲不平顺必须予以立即消除。为研究轨道扭曲不平顺,需要人为地设置量测基长与幅值见图2,以左轨扭曲起始为初始时刻,分别在左、右轨道上施加波长为L,幅值为A的半波余弦激励,同时左右轨激励相位相差半个周期。记列车运行时速为v,那么左、右钢轨顶面高度随时间的变化关系可分别用式(5)与式(6)表示。
(5)
(6)

图2 轨道扭曲不平顺Fig.2 Schematic diagram of track distortion
1.2 6自由度振动试验台结构
6自由度振动试验台由前、后两个子系统组成,如图3所示。这两个子系统结构相同,相互独立。试验时,可将单独的转向架落于单个子系统上,对转向架整体进行加载以测定转向架的各类动、静态参数;也可将转向架前、后轮对分别落于前、后子系统上,此时每条轮对可独立运动,可模拟轨道三角坑或线路曲线等工况对转向架加载以测定转向架的相关参数。

图3 6自由度振动试验台Fig.3 6DOF vibration test bench
6自由度振动试验台的具体结构,如图4所示。其中,试验台顶部与被测试对象刚性连接,每个作动器与试验台顶部通过上部球铰连接;各作动器下部球铰固接于试验台底座上,是空间不动点。通过协同控制振动台子系统各作动器的位移便可实现振动台顶部在空间6个自由度运动的解耦;对振动台前后子系统共12个作动器的协同控制,可实现试验台顶部在空间6个自由度运动的解耦。
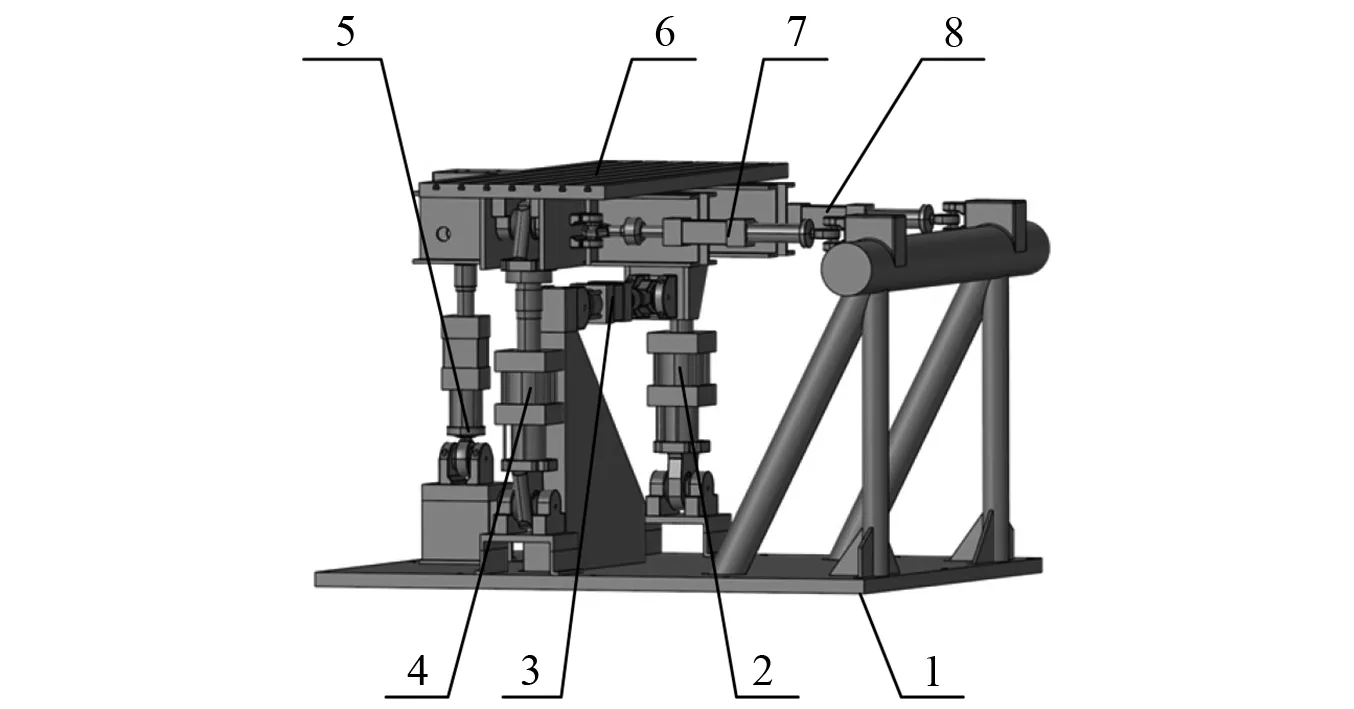
1.试验台底座;2.内侧垂向作动器;3.横向作动器;4.外侧垂向作动器;5.尾部点头垂向作动器;6.试验台顶部;7.外侧纵向作动器;8.内侧纵向作动器。图4 6自由度振动试验台子系统结构组成Fig.4 The composition of 6DOF vibration test bench subsystem
2 空间机构的位姿解算方法
已知6自由度振动平台各部分的空间初始位置,如何控制各作动器的位移量,使试验台顶部最终到达预期的空间位置。齐次坐标变换提供了一种有效的手段来解算空间机构的位置姿态与各个零部件之间的位移、速度和加速度关系[9-10]。
2.1 空间点的齐次坐标
设空间中有一点A,它在笛卡尔坐标系下的物理坐标为(x0,y0,z0),对于一个四维列向量[x1x2x3x4]T,当它里边的4个元素满足
(7)
此时,便称(x1,x2,x3,x4)为空间点A对应的齐次坐标。
2.2 齐次坐标变换
如图5所示,O-XYZ与O′-X′Y′Z′是空间中的两个直角坐标系,O′-X′Y′Z′可由O-XYZ经过平移与绕各轴旋转变换得到;其中,沿各坐标轴的平移可用一列向量[r1r2r3]T表示,用坐标轴X′,Y′,Z′相对于原始坐标轴X,Y,Z的方向余弦阵R表示坐标系旋转过的角度,该方向余弦阵可表示为
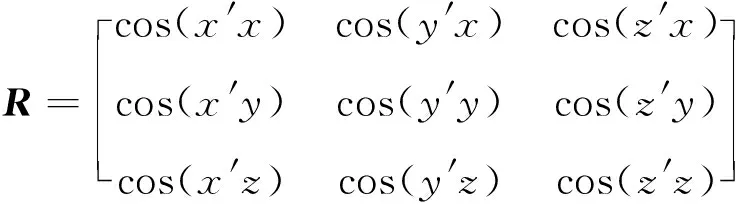
(8)
简记为
(9)
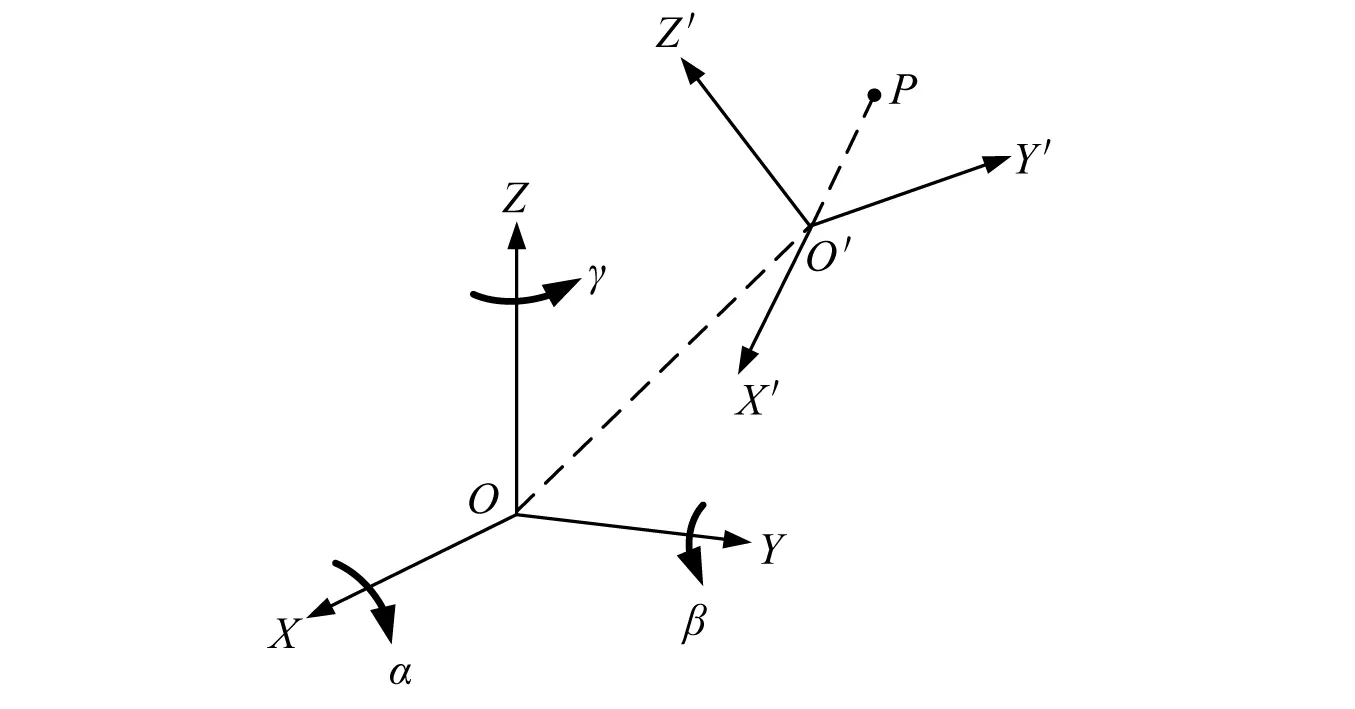
图5 空间坐标变换示意图Fig.5 The schematic diagram of space coordinate transformation
空间中的一点P,它在坐标系O-XYZ下的坐标为(x,y,z),它在坐标系O′-X′Y′Z′下的坐标记做(x′,y′,z′),那么二者之间的关系可以表示为
(10)
根据空间中点的齐次坐标的定义,在坐标系O-XYZ中,总能写出P点对应的齐次坐标(x1,x2,x3,x4), 在坐标系O′-X′Y′Z′中P点对应的其次坐标可记做(x′1,x′2,x′3,x′4),那么式(10)可改写为
(11)
式(1)可用矩阵形式表示为
(12)
简记为
(13)
式中,矩阵A为点的齐次坐标变换矩阵,该矩阵中包含了点的平动与转动信息。由此可见,点在空间中平动与转动后的位置可由齐次坐标变换矩阵与点的初始齐次坐标列向量相乘得到。
3 轨道几何不平顺在6自由度振动试验台上的复现
在振动试验台上复现轨道不平顺,也就是通过同时控制各个方向作动器的不同位移命令来使试验台顶部达到预期的空间姿态,关键是要得出各个作动器的长度变化量。因6自由度振动试验台前后两个子系统结构与驱动方式一致,故主要以其中一个子系统为例进行叙述。同时考虑到轨道方向不平顺与轨距不平顺都直接表现为左右钢轨相对于线路名义中心线的横向偏移,二者只是偏移量大小的计算方法不同而在振动试验台上的复现方法相同,故文中仅以轨道方向不平顺的复现为例对二者进行说明。
3.1 轨道高低不平顺试验台复现
选取初始时刻试验台顶部几何中心为坐标原点,在铁路坐标系中规定:沿着列车前进方向为纵向,即为坐标轴x轴;列车宽度方向为横向,即为坐标轴y轴;垂直oxy平面向下记做z轴。试验台各部分到坐标原点的位置如表1所示,其中,数值列中第一列为各作动器下球铰中心点到坐标原点的距离,数值列中第二列为各作动器上球铰中心点到坐标原点的距离。

表1 作动器球铰空间坐标Tab.1 Spherical joint coordinates of actuator
将各个作动器的下球铰中心点在空间中的齐次坐标写成矩阵形式,记作:C0
(14)
将初始时刻各个作动器上球铰中心点在空间中的齐次坐标写成矩阵形式,记作:C′0
(15)
则初始时刻各作动器的长度可表示为
L0=‖C′0-C0‖
(16)
由式(1)可知,轨道高低不平顺直接表现为钢轨顶面相对于水平面的高低起伏,其起伏振动的幅值可由左右钢轨相对于线路名义中心线高度差的平均值Zv来表示。因此,可通过控制试验台上部平台随时间的垂向平动来模拟轨道高低不平顺。
由2.2节可知,试验台上下平动时,各点坐标旋转的方向余弦矩阵是一个单位矩阵,平台顶部各点的平动可表示为
L=[0 0z]T
(17)
因此,平台在做上下平动时的齐次坐标变换矩阵A表示为

(18)
试验台平动后各作动器顶部球铰中心点的坐标值用矩阵形式表示为
C′a=AC′0
(19)
各作动器的伸长量ΔL用矩阵形式可表示为
ΔL=‖C′a-C0‖-L0
(20)
3.2 轨道方向不平顺试验台复现
由式(3)可知,轨道方向不平顺直接表现为钢轨内侧面相对于理想平直轨道中心线的横向偏移,其横向偏移振动的幅值可由左右钢轨各自横向偏移量的平均值来ya表示。因此,可通过控制试验台上部平台随时间的横向平动来模拟轨道方向不平顺。
由2.2节可知,试验台横向平动时,表示各点坐标旋转的方向余弦矩阵是一个单位矩阵,平台顶部各点的平动可表示为
L=[0y0]T
(21)
同理可写得平台在做上下平动时的齐次坐标变换矩阵A,根据横向偏移齐次坐标变换矩阵求得试验台横向平动后各作动器顶部球铰中心点的坐标值,进而求得各作动器的伸长量。
3.3 轨道水平不平顺试验台复现
轨道水平不平顺会使车辆产生侧滚振动。因此直接控制试验台顶部绕轴转动来复现轨道水平不平顺。假设左侧钢轨与右侧钢轨顶面各自偏离线路名义中心线的的高度分别为Zl,Zr,左右轮轨接触点横向间距为2b,那么车辆的侧滚角度θ可表示为
(22)
当试验台绕x轴侧滚时,平台顶部各点的平动位移组成的矩阵L=[0 0 0]T。规定平台逆时针旋转角度为正,则平台顶部绕x轴旋转的方向余弦阵R可表示为

(23)
平台在做绕x轴旋转时的齐次坐标变换矩阵A可表示为
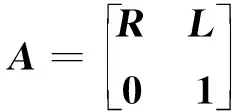
(24)
试验台转动后各作动器顶部球铰中心点的坐标值用矩阵形式表示为
C′a=AC′0
(25)
试验台转动到空间任一位置时,各作动器的伸长量ΔL用矩阵形式可表示为
ΔL=‖C′a-C0‖-L0
(26)
3.4 列车运行速度模拟
实测得到的轨道不平顺通常由空间域的位移信号组成,信号曲线的横坐标为轨道长度,纵坐标为安装在转向架轴端的位移传感器采集到左、右轨垂向位移信号或横向位移信号[11]。但是振动试验台的激励输入信号是基于时间域的,因此需要先将空间域的信号转化到时间域。具体转化方法如式(27)所示
(27)
式中:t为列车通过某段不平顺激扰的时间;λ为轨道长度;v为列车运行速度。
由式(27),结合频率与时间的关系可知,列车运行速度越高,轨道不平顺激扰对列车的激振频率越高。因此,通过改变振动台激励输入信号的频率即可实现对列车运行速度的模拟。
3.5 轨道扭曲不平顺试验台复现
轨道扭曲不平顺的产生原因是左右钢轨交替存在水平差,带来的直接影响是列车同一个转向架的前后两条轮对,共4个车轮不在同一平面。因此在复现扭曲不平顺时可通过控制同一转向架前后轮对的不同运动来实现,而这需要试验台前后两个子系统各自带动一条轮对来实现。与轨道水平不水平顺类似,当同一截面的左右钢轨存在水平差时,会导致通过该段轨道的轮对发生侧滚。设转向架前后轴距为l,车速为v。记前轮对左、右车轮所在钢轨顶面相较于线路名义中心线的高度分别为zl与zr,则zl与zr可分别按照式(5)与式(6)计算,那么前轮对的侧滚角度仍可按照式(22)计算;此时后轮对左、右车轮所在钢轨顶面相较于线路名义中心线的高度可表示为
(28)
(29)
将zl2与zr2代入式(22)便可得到同一时刻下后轮对的侧滚角度,前后轮对侧滚角度存在的相位差导致了4个车轮不共平面,即模拟了轨道扭曲不平顺。
4 轨道几何不平顺复现方法验证
4.1 6自由度试验台虚拟样机模型
利用多体动力学分析软件SIMPACK搭建了6自由度试验台的虚拟样机模型[12],如图6所示。忽略试验台微小的弹性变形,将各零部件都当作刚体处理。试验台底座完全约束,各作动器尾部通过球铰单元约束于底座上,具有3个方向的转动自由度;各作动器顶部通过球铰单元约束于平台顶部,具有3个方向的转动自由度;通过时间函数驱动作动器伸出缸在缸体内运动。试验台顶部具有6个运动自由度,其运动姿态完全取决于各个方向作动器共同驱动的效果。
4.2 基于实测轨道几何不平顺的试验台位姿反解
以实测的武广高速铁路轨道不平顺样本为例验证轨道高低不平顺、方向不平顺与水平不平顺的复现方法。该轨道不平顺样本是基于空间域的位移信号,信号曲线的横坐标为轨道长度,纵坐标为左、右钢轨垂向位移信号与横向位移信号[13],样本采集过程中,轨检车的运行速度为245 km/h,采样点间隔0.25 m,样本点数为4 096点。以左轨垂向不平顺与左轨横向不平顺信号为例,信号曲线如图7、图8所示。

图6 6自由度振动试验台虚拟样机模型Fig.6 The virtual prototype model of 6DOF vibration test bench
根据式(27),将实测的空间域信号转化为时域信号。如图9、图10所示为根据车速为250 km/h为例换算得到的左轨垂向不平顺与左轨横向不平顺时域信号曲线。

图7 左轨垂向不平顺空间域信号曲线Fig.7 Signal curve of left rail vertical irregularity in spatial domain

图8 左轨横向不平顺空间域信号曲线Fig.8 Signal curve of left rail lateral irregularity in spatial domain

图9 左轨垂向不平顺时域信号曲线Fig.9 Signal curve of left rail vertical irregularity in time domain

图10 左轨横向不平顺时域信号曲线Fig.10 Signal curve of left rail lateral irregularity in time domain
根据式(1)~式(4),对实测的左右轨不平顺信号叠加处理,得到基于轨道中心线的轨道不平顺时域信号。根据轨道不平顺的类型,利用相应的齐次坐标变换矩阵处理轨道不平顺时域信号,已知试验台初始位置和各个时刻的目标位置,反解得到基于时间域的各作动器位移控制信号。如图11、图12 所示为复现轨道水平不平顺时内侧垂向作动器与横向作动器的控制信号。
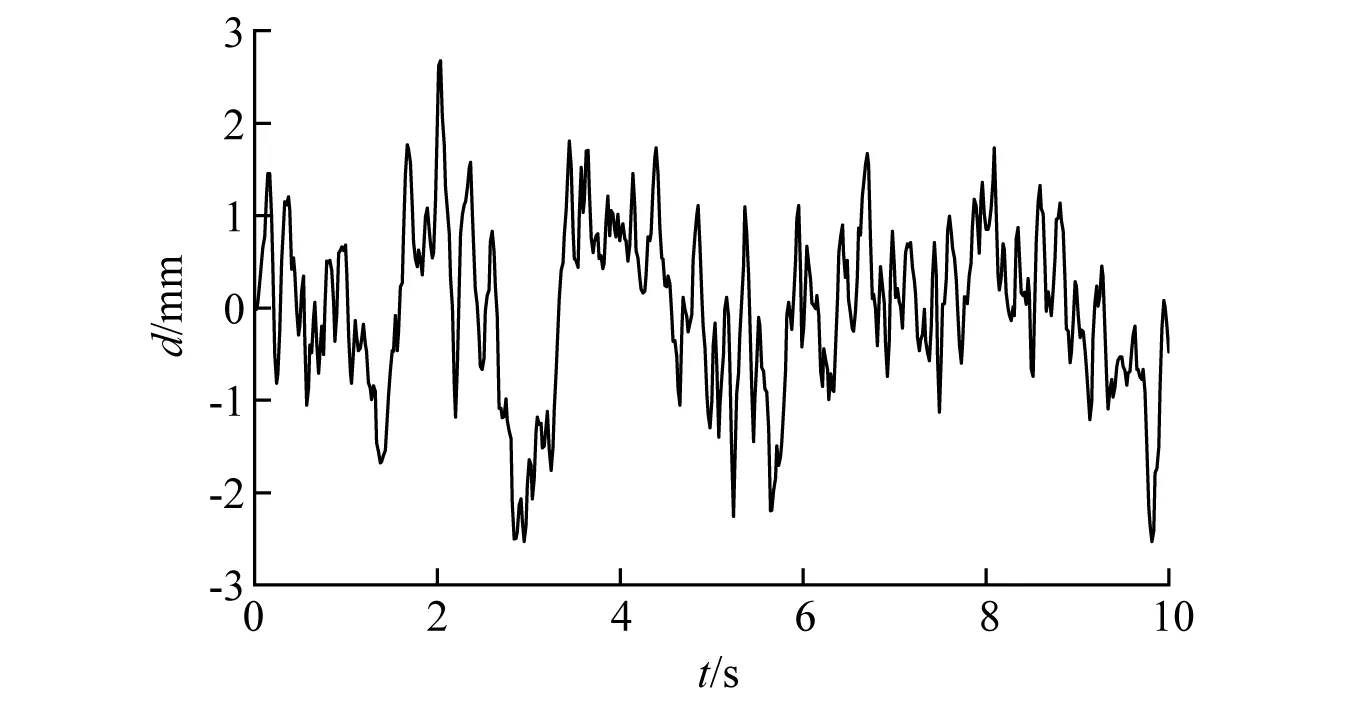
图11 内侧垂向作动器控制信号Fig.11 Control signal of inner vertical actuator
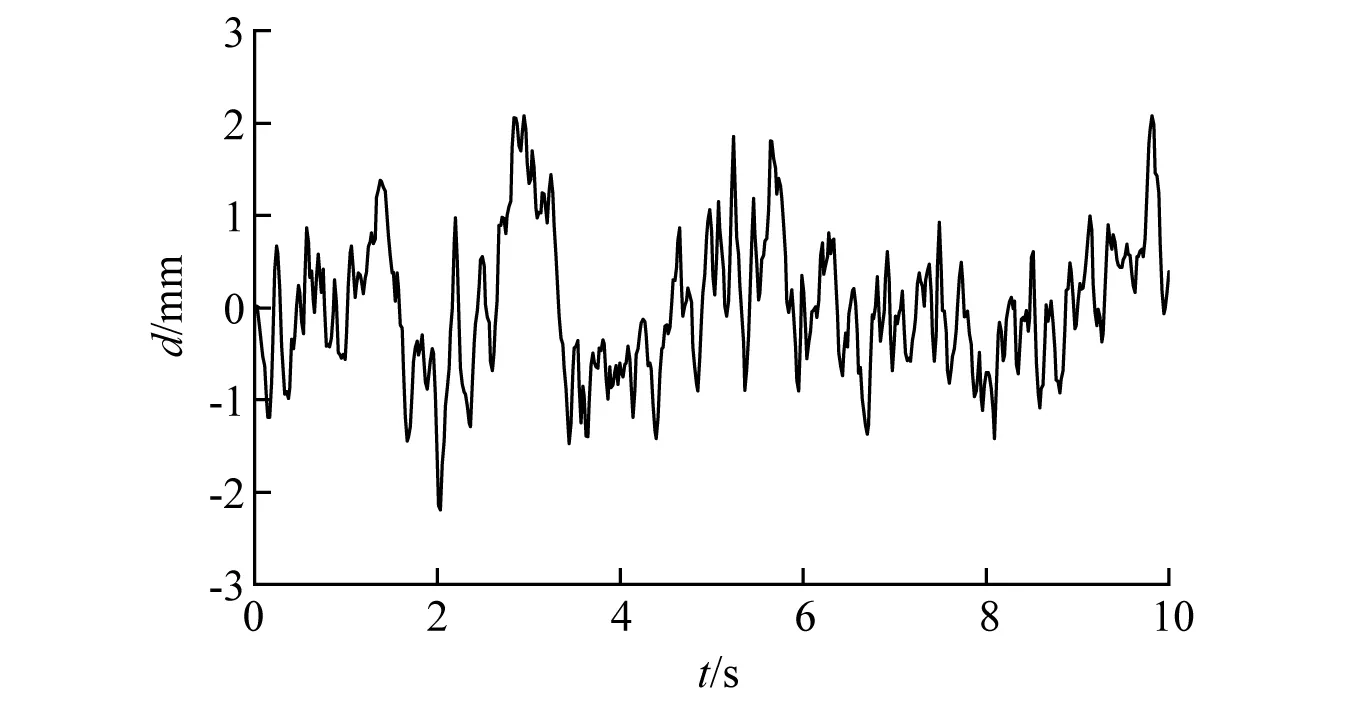
图12 横向作动器控制信号Fig.12 Control signal of inner lateral actuator
4.3 轨道扭曲不平顺复现试验台位姿反解
设置线路扭曲不平顺量测基长为6.25 m,扭曲不平顺最大幅值为2A为10 mm。取转向架前后轴距为2.5 m,运行速度为250 km/h,根据式(5)与式(6)得到线路的扭曲不平顺状态时域曲线,如图13所示。根据式(22)将一、二位轮对左右车轮的高度差分别转化一、二位轮对各自的侧滚角,如图14所示。控制试验台一、二位子系统分别带动转向架一、二位轮对侧滚,已知试验平台各自侧滚角度随时间的变化关系,根据3.3节解算得到两个子系统各作动器的控制命令。如图15所示为复现轨道扭曲不平顺时一、二位子系统各自内侧垂向作动器的控制信号。
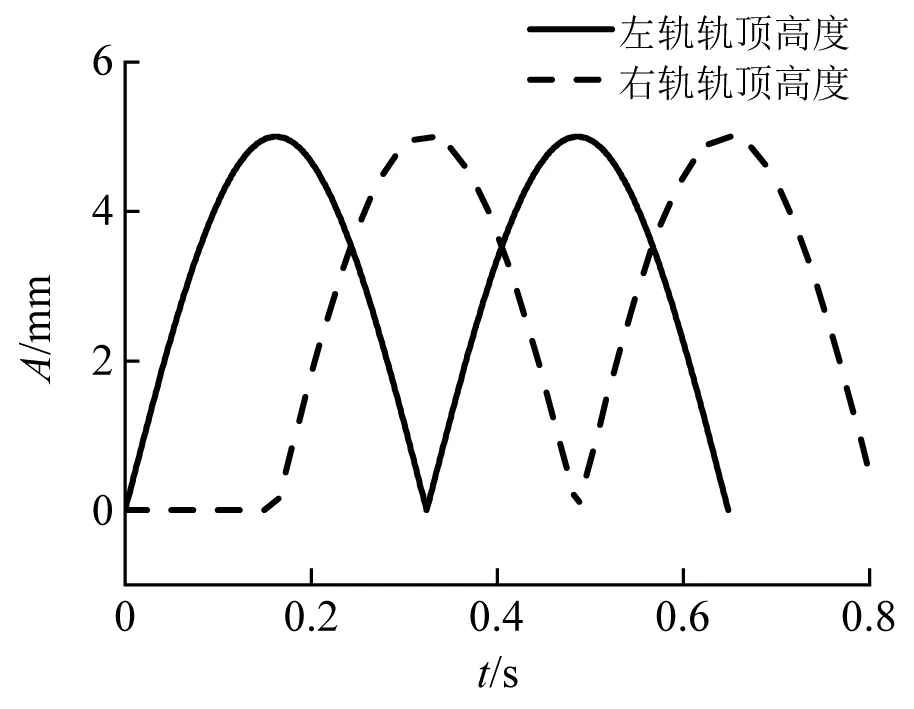
图13 线路扭曲实施例Fig.13 A specific example of track distortion

图14 轮对侧滚角Fig.14 Roll angle of wheelsets
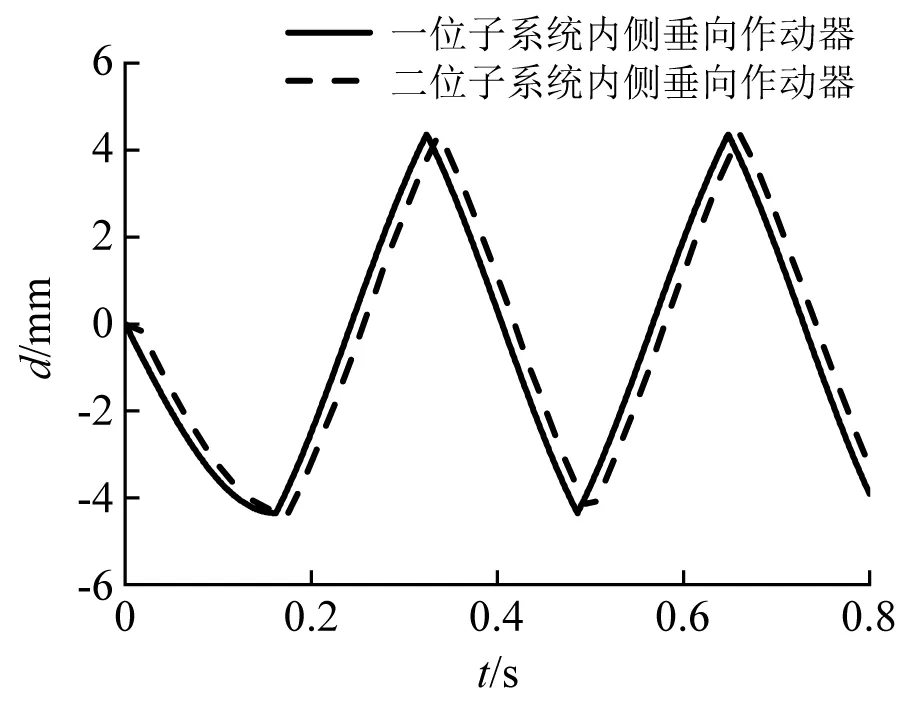
图15 扭曲线路模拟时的作动器控制信号Fig.15 Actuators control signal to simulate the distortion
4.4 轨道几何不平顺复现方法验证
将各作动器控制命令导入试验台虚拟样机中,驱动各作动器伸出缸动作,带动试验台顶部运动,模拟轨道几何不平顺。将试验台顶部仿真后的时间-位移曲线输出,与实测的基于轨道中心线的轨道几何不平顺曲线对比。各轨道几何不平顺的复现值与线路实测目标值的对比分别如图16~图19所示。
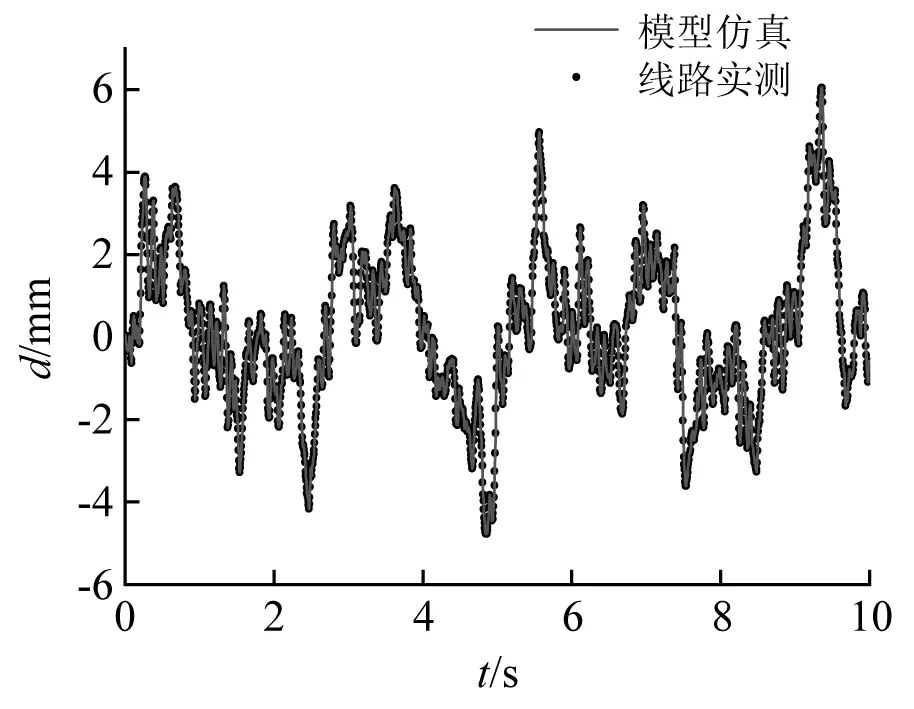
图16 轨道高低不平顺试验台复现结果Fig.16 Reappearance result of rail vertical irregularity in test bench
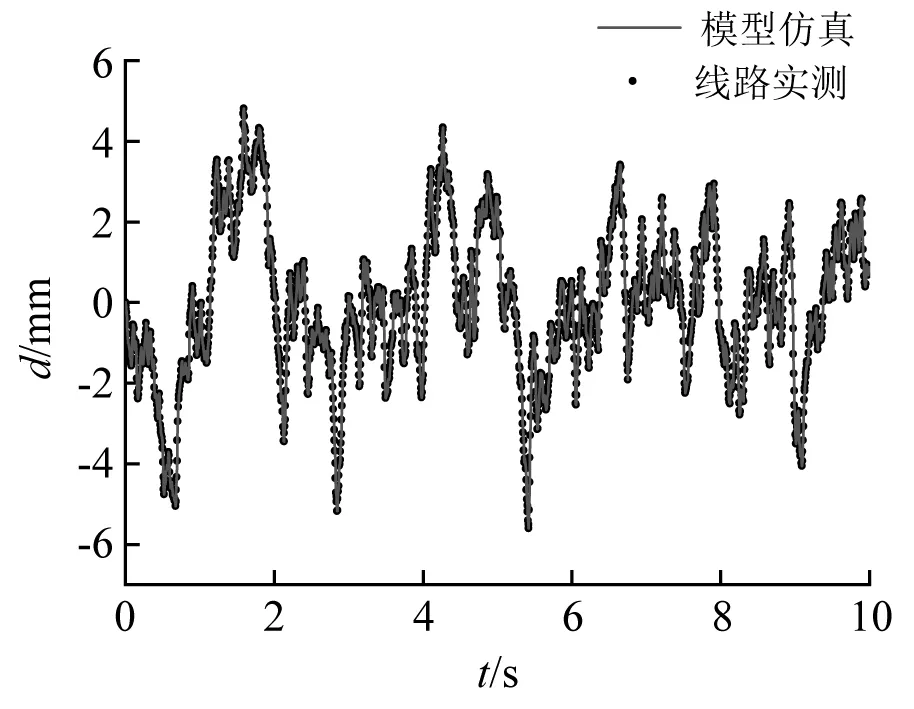
图17 轨道方向不平顺试验台复现结果Fig.17 Reappearance result of rail lateral irregularity in test bench
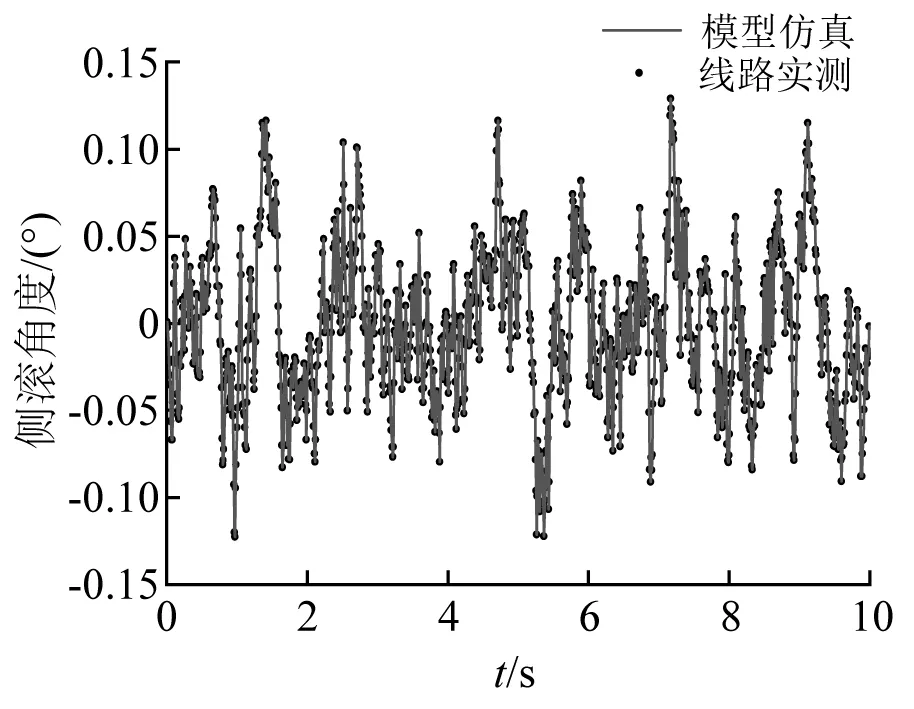
图18 轨道水平不平顺试验台复现结果Fig.18 Reappearance result of rail horizontal irregularity in test bench
由图16~图19可以看出,试验台顶部运动平台的实际运动姿态与目标值的一致性较好。保持试验台运动仿真中的采样频率与实测轨道不平顺采样频率一致,将同一时刻下运动平台的实际位移值与目标位移值做差,得到两者间的数值偏差,各类轨道几何不平顺复现时的数值偏差分别如图20~图22所示。可看出,任意时刻下,试验平台的运动姿态与目标值之间的相对误差较小,可以认为试验平台控制命令的解算方法是无误的,而产生误差的原因主要是因为模型搭建的几何误差导致,而在实际中误差或将产生于试验台自身的安装误差。
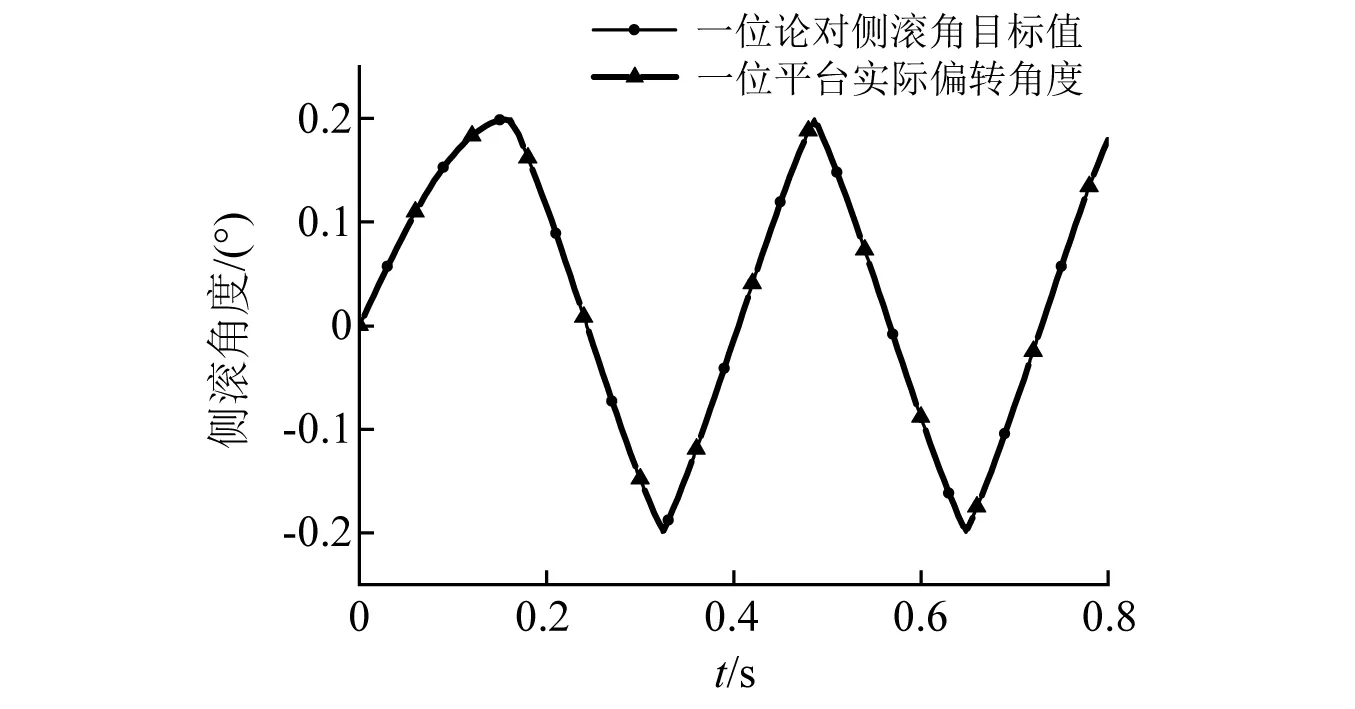
图19 轨道扭曲不平顺试验台复现结果Fig.19 Reappearance results of track distortion in test bench
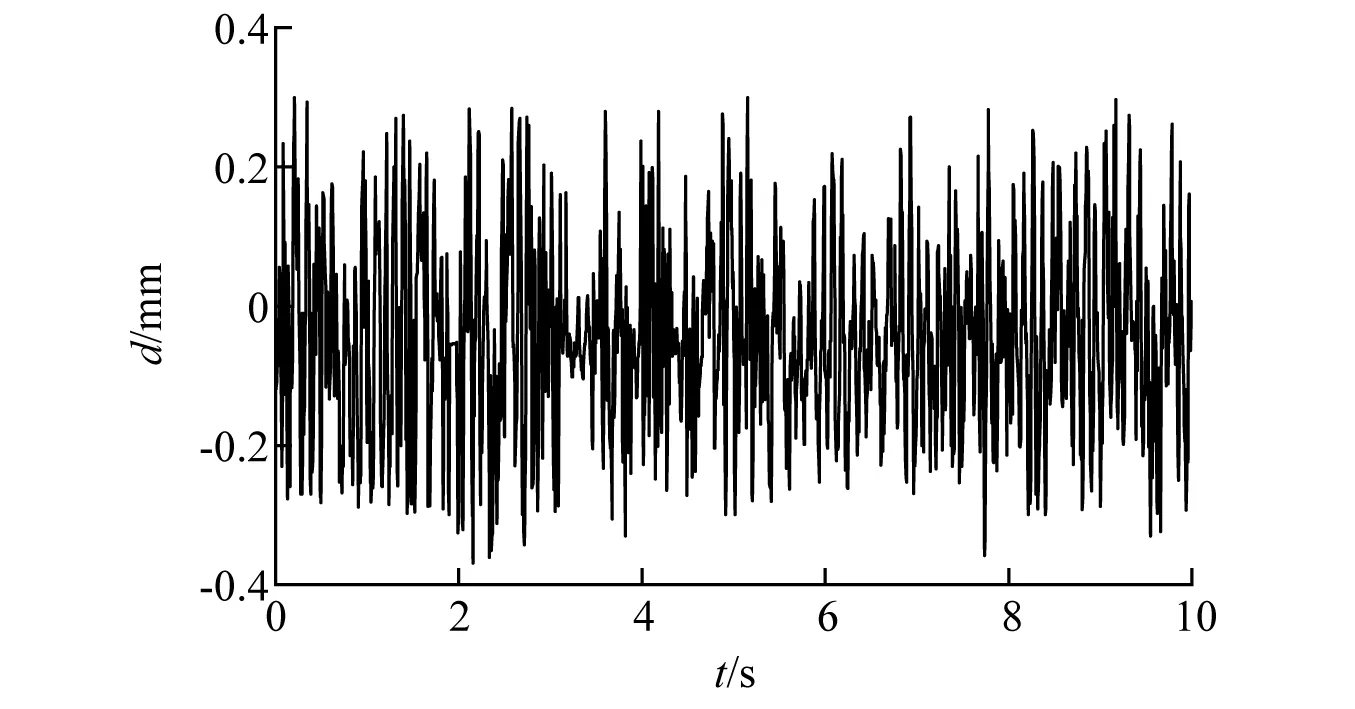
图20 轨道高低不平顺复现数值误差Fig.20 Numerical error in the reappearance of rail vertical irregularity

图21 轨道方向不平顺复现数值误差Fig.21 Numerical error in the reappearance of rail lateral irregularity
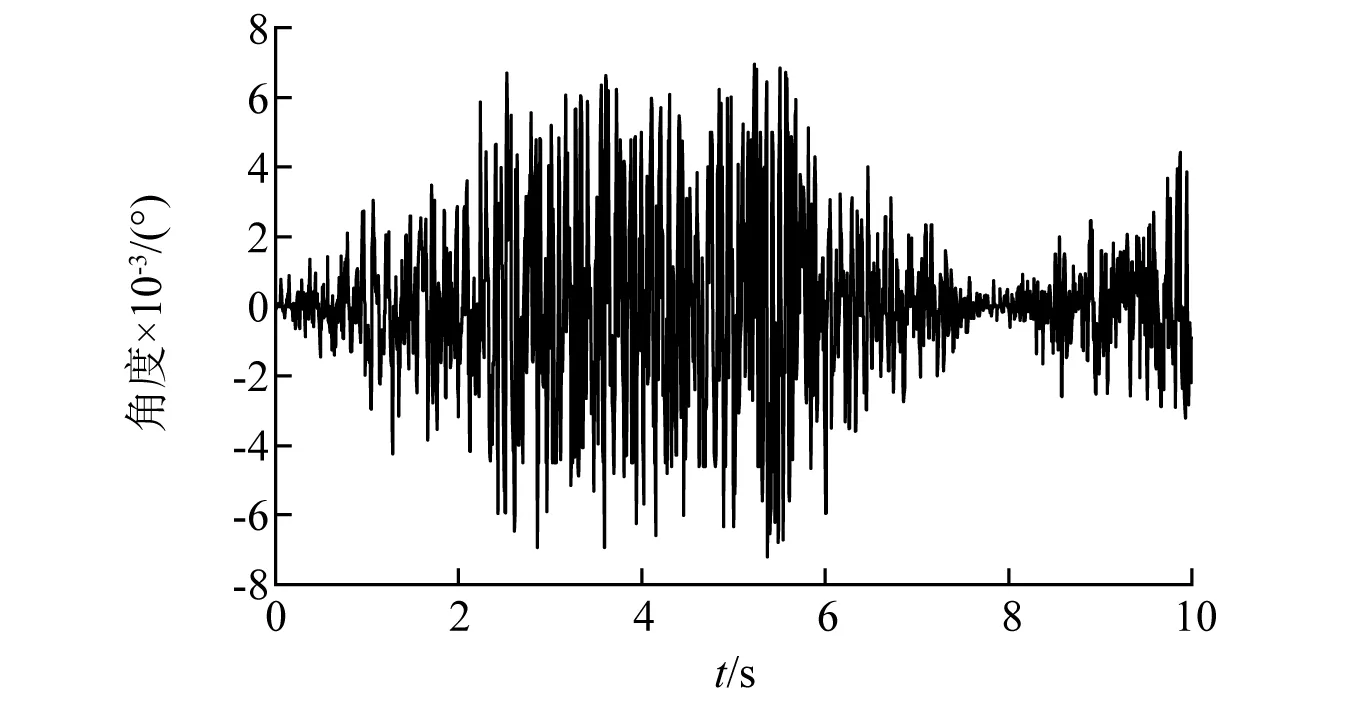
图22 轨道水平不平顺复现数值误差Fig.22 Numerical error in the reappearance of rail horizontal irregularity
5 轨道几何不平顺复现在转向架构架模态参数识别中的应用
常规的模态试验激励方式有激振器激励和力锤激励,但整备状态下的转向架由于质量大、刚度大等原因,采用常规的激振器激励很难激发起构架的高阶固有模态,采用力锤激励又容易造成过载或连击。因此在振动试验台上模拟实际轨道激扰,通过转向架惯性加载对转向架构架进行模态参数识别。
5.1 虚拟试验模型搭建
以某型整备状态下的转向架构架模态参数识别为例,在已建立的6自由度振动试验台虚拟样机模型的基础上,增加整备状态下的转向架刚柔耦合动力学模型,如图23所示。将转向架轮对固定在试验平台顶部,通过控制试验台顶部带动转向架振动,模拟实际线路中轨道不平顺对转向架的激扰。为拾取振动过程中转向架构架的加速度信号,在转向架构架上表面布置了44处加速度测点,如图24所示。

图23 带转向架刚柔耦合动力学模型的试验台Fig.23 The test bench attaches the rigid-flexible coupling modal of bogie

图24 转向架构架表面加速度测点Fig.24 Acceleration measuring points on bogie frame
5.2 虚拟试验台控制信号解算
选择实测的武广高速铁路不平顺信号作为试验台输入,3.1~3.3节中针对不同类型的轨道随机不平顺分别进行了复现,但实际线路中,各种不同类型的轨道随机不平顺是同时存在的,因此式(13)中的齐次坐标变换矩阵A中需要同时包含沿各坐标轴的平动信息与转动信息。具体地,矩阵A可表示为
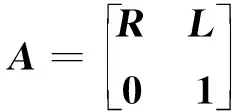
(30)

以车速为250 km/h对实测的空间域轨道不平顺信号进行空-时信号转换,进而根据式(19)与式(20)对该时域信号反解得到各作动器的控制信号。
5.3 转向架构架模态参数识别
为了更有效地对虚拟试验得到的模态参数进行辨识与验证,建立了转向架构架有限元模型[14]。转向架一系悬挂采用弹簧单元模拟,弹簧刚度与转向架动力学模型中的刚度一致,采用梁单元模拟轮对,动力学模型中的轮对是固定在试验台表面的,所以有限元模型中仅约束4个车轮的绕轴转动自由度,对该有限元模型进行模态计算,得到构架前八阶固有频率与振型如图25(a)~图25(h)所示。

图25 有限元模态计算结果Fig.25 The modal reasult calculated with finite element model
利用LMS Test. Lab对虚拟试验输出的各加速度测点的加速度信号处理得到构架模态参数识别稳态图,如图26所示。根据模态置信准则,剔除MAC矩阵中对非对角元素影响较大的可能为虚假的振型,最后提取得到构架的四阶模态,频率分别为18 Hz,67 Hz,85 Hz与97 Hz,各阶模态对应的振型如图27(a)~图27(d)所示,各阶模态振型对应的MAC矩阵如图28所示。通过对比虚拟试验得到的构架模态识别结果与有限元计算结果可知,虚拟试验得到的第一阶、第三阶与第四阶模态分别与有限元计算结果的第一阶、第六阶以及第七阶模态的频率与振型一致,可以确定为同一阶模态;而虚拟试验识别得到的第二阶模态振型与有限元计算结果的第八阶模态振型一致,但频率相差较大,为确定二者是否为同一阶模态,对二者进行相关性分析,得到虚拟试验识别的构架第二阶模态与有限元计算得到的第八阶模态之间的相关度为88%,可以认为二者是同一阶模态,二者频率之间的差异可能是有限元计算模型边界条件与虚拟试验不同导致的,如有限元计算时采用了梁单元来模拟实际轮对,采用了刚性单元模拟转向架带有一定刚度值的转臂定位节点。可根据虚拟试验的结果来对有限元计算模型调整,以使有限元计算结果与虚拟试验结果更加接近。
因此,在该段选定的轨道几何不平顺激励下,当列车以250 km/h速度运行时,会激发出转向架构架的侧滚模态(18 Hz)、构架侧梁反对称弯曲模态(67 Hz)、侧梁横向同向弯曲模态(85 Hz)以及构架侧梁同向垂向弯曲与横梁垂向弯曲共存模态(97 Hz)。
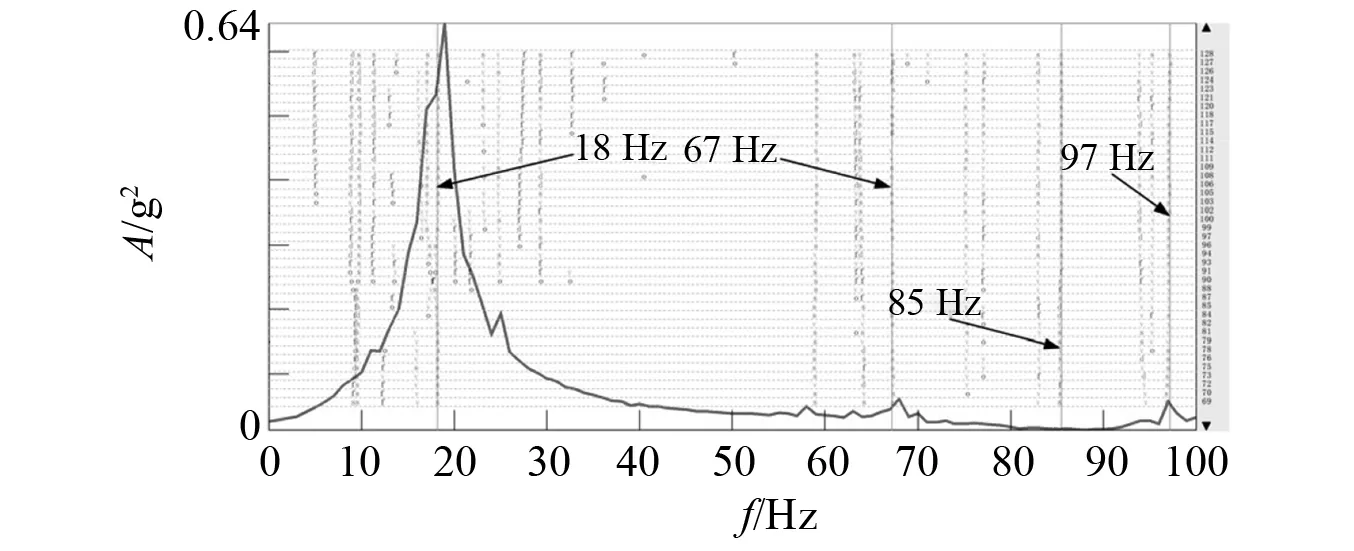
图26 稳态图Fig.26 The steady state diagram
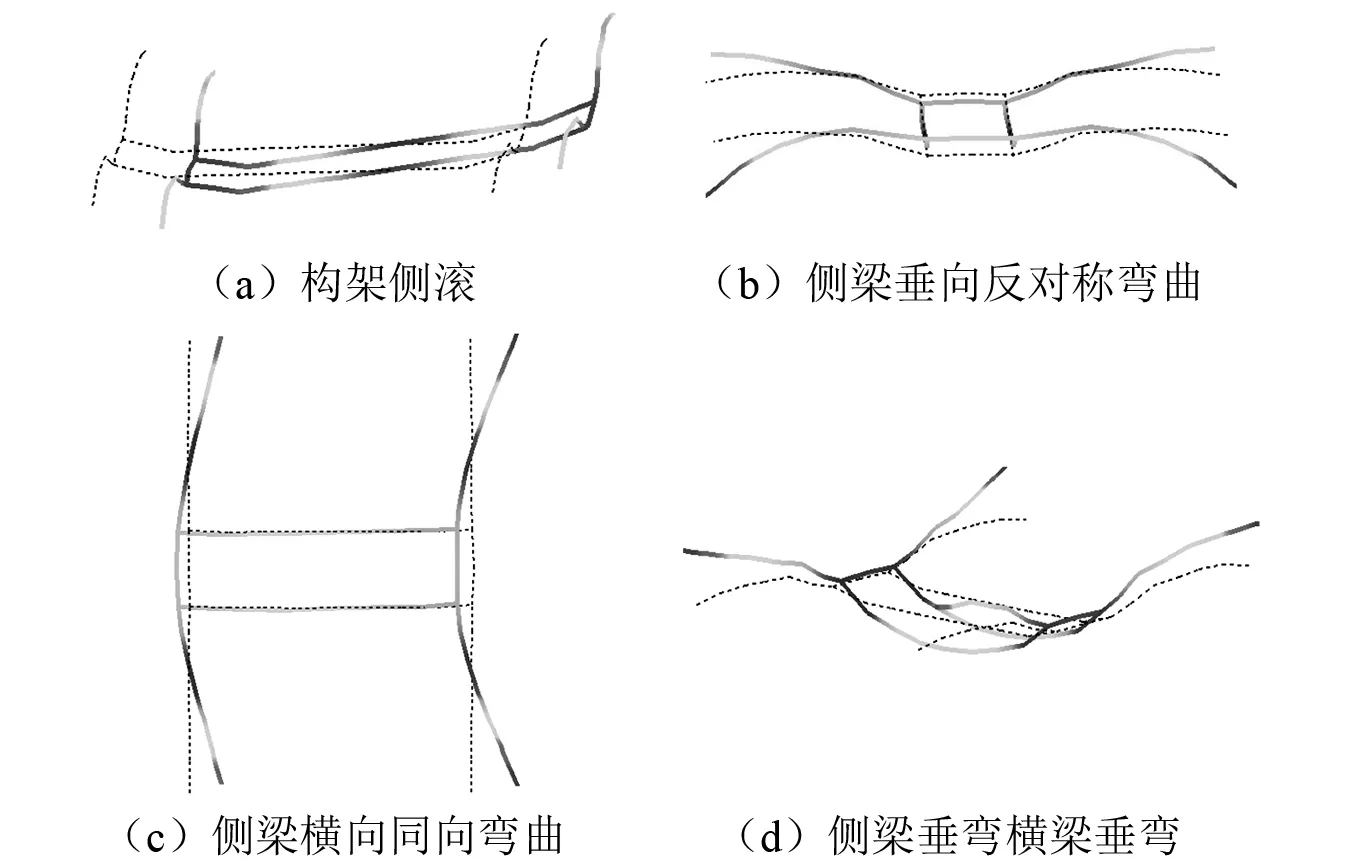
图27 轨道几何不平顺激励下的构架模态振型Fig.27 The mode shape of bogie frame under the track geometric irregularity excitation
6 结 论
对轨道几何不平顺在振动试验台上的复现方法进行了研究,利用该方法在振动试验台全尺寸虚拟样机模型上对实测的武广高速铁路不平顺进行了复现。
(1) 从复现结果可以看出,振动试验台对实测的轨道几何不平顺信号复现程度较高,利用齐次坐标变换对试验台在空间中的位姿解算是准确的。
(2) 模拟线路试验,利用在振动试验台上复现的轨道几何不平顺信号作为激励,对某一型号整备状态下的转向架构架进行工作模态识别,得到列车在该路段以给定的速度运行时,会激发出转向架构架的侧滚模态与其中三阶弯曲振动模态。
(3) 在振动试验台上可复现各种不同线路实测的轨道不平顺,通过改变激励频率模拟列车运行时的各种速度等级,进而测试转向架或车体在不同振动环境下的振动响应,了解系统的振动特性。

