流冰撞击作用下川藏铁路桥梁振动抑制及行车安全研究

李鹏浩， 翟婉明， 和振兴， 石广田

(1. 兰州交通大学 机电工程学院，兰州 730070； 2. 西南交通大学 牵引动力国家重点实验室，成都 610031)

川藏铁路是我国西南地区在建的重要铁路干线，连接成都和拉萨，新建正线长约1 549 km，设计时速160～200 km/h。川藏铁路沿线地区环境气候多变、地质复杂、灾害频发，具有高寒缺氧、高烈度地震、高海拔和大高差等“三高一大”的特征[1-3]。川藏铁路沿线的部分桥梁面临着来自冰湖溃决和冰融季节时河流和湖泊中流冰的撞击。与车辆、船舶、泥石流和落岩等撞击不同[4-7]，流冰撞击桥墩时产生的撞击力相对较小，但具有持续时间较长，撞击频率高等特点，撞击危害不能忽视。桥梁受到撞击时，会产生梁体相对支座的偏移，严重时甚至导致支座损坏，给桥梁结构带来安全隐患[8-9]；流冰撞击还会影响桥上轨道结构的平顺性，由此引起的动态轮轨力会随车速的增加而显著增大，可能对乘客的乘坐舒适性和列车的运行安全性造成影响[10]。

车桥振动是铁路动力学的经典课题，经过几十年的发展，形成了两种典型的模型：车-桥耦合振动和列车-轨道-桥梁动力相互作用[11-13]。近年来，许多学者基于列车-轨道-桥梁动力相互作用理论，评估了各类桥梁的动力学性能以及桥上列车的走行性和安全性；也有一些学者提出新的混合求解算法，旨在提高计算精度和效率[14-15]。除了研究车-线-桥系统的自激振动外，外部环境激励对车-线-桥系统的影响也引起广泛关注，如强风、地震和撞击等[16-17]。Xia等[18-19]研究了流冰撞击对车-桥系统的影响，评估桥上列车运行安全性，并分析了行车速度和撞击强度的阈值关系。当流冰撞击强度和列车速度到一定限值时，桥上列车存在脱轨的危险。

动力吸振器(dynamic vibration absorbers，DVA)是一种常用的减振装置，它由质量块、弹簧和阻尼器组成，具有简单、可靠、廉价的特点，近年来被广泛应用于土木结构振动控制领域。Frahm[20]于1911年提出了在单自由度结构上附加无阻尼DVA，这是DVA的首次应用。Ormondroyd等[21]在Frahm发明的DVA基础上加入了阻尼器，这样不仅增强了减振效果，还拓宽了减振频带，并提出了著名的定点理论。Hahnkamm[22]依据定点理论推导了DVA的最优频率比和最优阻尼比。Zhu等[23]研究了动力吸振器对浮置板轨道的低频振动控制，振动控制效果显著。杨吉忠等[24-25]基于动力吸振原理研究了高墩桥梁的抗震特性并分析了列车过桥的安全性，得出动力吸振型桥梁在地震荷载作用下减振效果突出的结论。

目前DVA减振技术在桥梁工程中多用在桥梁抗震领域，而关于撞击荷载作用下DVA减振控制未见研究。为了研究DVA对流冰撞击作用下桥梁的振动抑制和对列车行车安全性的影响，本文组织结构如下：第1章概述列车-轨道-桥梁-冰击模型理论；第2章介绍DVA设计方法；第3章研究DVA对冰击荷载作用下桥梁结构的振动抑制；第4章分析DVA对冰击荷载作用下列车行车安全性的影响。

1 流冰撞击作用下列车-轨道-桥梁动力相互作用模型

基于列车-轨道-桥梁动力相互作用仿真框架[26-27]，流冰撞击作用下的列车-轨道-桥梁系统由列车和轨道-桥梁两个子系统组成。子系统之间通过轮轨相互作用和桥轨相互作用耦合。模型中有两个激励源：轨道几何不平顺引起的自激激励和作为外荷载施加到大系统中的流冰撞击力。动力学模型如图1所示。

图1 列车-轨道-桥梁-冰击动力学模型Fig.1 Dynamics model of train-track-bridge system under floating ice impact loads

1.1 车辆模型

车辆模型由1个车体、2个构架和4个轮对组成。车体、构架和轮对各有5个自由度，车辆模型共35个自由度。车辆动力学方程为

(1)

1.2 轨道-桥梁模型

模型中左右两股钢轨被视为连续的Timoshenko梁，考虑了钢轨的垂向、横向和扭转振动，计算中为模拟轨道板和钢轨之间的力学关系，采用离散黏弹性单元模拟了扣件的刚度和阻尼特性。桥梁采用有限元方法建模，主梁和桥墩均采用实体单元。建模中假定：①桥梁模型与实际工程中结构吻合，在不影响主要力学性能的前提下进行一定的简化；②桥梁在撞击过程中只发生小变形，结构始终处于线弹性范围。轨道-桥梁动力学方程表示为

(2)

桥梁结构阻尼采用Rayleigh阻尼。假定结构的阻尼矩阵是质量矩阵和刚度矩阵的组合，即

C=αMb+βKb

(3)

(4)

式中：ωi和ωj分别为桥梁结构的第i和第j阶参考频率[28]；ζb为桥梁的阻尼比。

1.3 轮轨接触关系

本文采用新型轮轨空间耦合模型[29]来模拟轮轨非线性接触几何关系，轮轨法向力用赫兹非线性理论计算，轮轨切向力采用kalker线性蠕滑理论计算[30]。

1.4 流冰撞击荷载

流冰撞击荷载通常由两种方法获得：一是现场试验采集撞击力；二是通过有限元法仿真获得。本文通过建立流冰-桥墩撞击模型计算了流冰撞击荷载。桥墩采用线弹性材料模拟，参考河冰单轴压缩试验数据[31]，冰排采用与应变率相关的塑性材料模拟，以最大拉应力作为冰排破坏失效准则。

将计算得到的流冰撞击力作为外部荷载施加到列车-轨道-桥梁系统中，此时桥梁子系统的动力学方程为

(5)

式中，Rc为流冰撞击力。

2 DVA设计方法

在进行DVA减振系统设计时，需确定DVA的三个主要参数：质量比、刚度和阻尼。图2所示为随机激励作用下单自由度结构-DVA减振系统力学模型。

图2 随机激励作用下主结构-DVA减振模型Fig.2 DVA-primary structure subject to a random excitation

根据达朗贝尔原理，DVA作用下系统的运动方程为

(6)

式中：m1，k1，c1分别为主结构的质量、刚度和阻尼系数；m2，k2，c2分别为DVA的质量、刚度和阻尼系数；x1为主结构位移；x2为DVA位移；F(t)为外部随机荷载。

基于定点理论，Ormondroyd等推导出附加在单自由度带阻尼结构上的DVA的最佳刚度和阻尼解析式

(7)

由于桥梁是一个连续体结构，计算单自由度系统DVA最优参数的方法不能直接用于桥梁结构的DVA设计。文献[32]将经典的Den Hartog方法推广到多自由度结构，并推导出了最佳设计参数和最佳安装位置。本文参考文献[33]，将桥梁结构离散成一个多自由度系统，再基于模态分析、等效质量识别法，建立了由多个单自由度系统组成的非耦合系统。因此采用单自由度系统DVA的设计方法，可以设计桥梁结构上施加DVA的最优参数。

(8)

式中：mij为桥梁结构第i阶模态j点处的等价质量；T为系统动能；ωi为第i阶固有频率； {X1…Xj…XN}为系统特征向量；{M1…Mj…MN}为离散的单自由度质量；kij为桥梁结构第i阶模态j点处的等价刚度。

由式(7)、式(8)可知，当求得DVA质量比μ、桥梁结构等价刚度kij和等价阻尼cij后，即可求出DVA的最佳刚度和阻尼。但桥梁结构的等价阻尼cij很难通过计算求得，因此不能直接采用式(7)得到DVA的最佳刚度。式(9)所示为无阻尼单自由度结构附加DVA的最佳刚度计算公式

(9)

参考文献[34]可知，可先采用式(9)计算出一个初始刚度值，再根据最优同调条件，适当调小初始刚度来获得DVA的最佳刚度值。

3 桥梁撞击振动抑制

3.1 结构模型及动力特性分析

以川藏铁路典型的简支箱梁为例，采用ANSYS建立桥梁有限元模型，截面尺寸和桥梁布置如图3所示。建模中主梁和桥墩均采用solid65单元，网格尺寸0.4 m×0.4 m×0.4 m，桥面二期恒载作为附加质量分布到桥面上，采用mass21单元模拟，取值120 kN/m。为准确模拟桥梁支座和基础的作用，主梁和支座、桥墩和基础的连接采用弹簧单元模拟，该力元可以有效模拟支座和基础的刚度和阻尼特性。

图3 典型铁路简支箱梁结构 Fig.3 The typical railway simply-supported box girder structure

采用ANSYS对上述有限元模型进行模态分析，因流冰撞击主要影响桥梁结构的横向振动，因此本文只分析桥梁的横向振动模态，图4所示为桥梁前两阶横向振型。

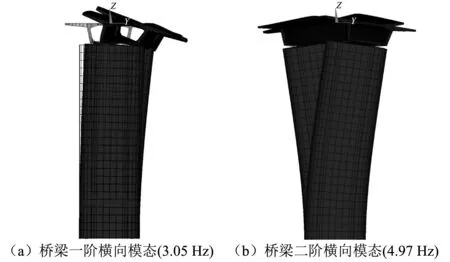
图4 桥梁前两阶横向振动模态Fig.4 The first two lateral mode shapes of the bridge

3.2 流冰撞击荷载计算

本文采用LS-DYNA建立流冰-桥墩撞击有限元模型，冰排尺寸为40 m×20 m×0.4 m。建模中桥墩和冰排均采用solid164单元模拟，桥墩单元尺寸为0.4 m×0.4 m×0.4 m，冰排中间部分单元大小为0.15 m×0.15 m×0.2 m，冰排两端单元尺寸大小为0.15 m×0.4 m×0.2 m，冰排撞击位置为距墩底5 m处。模型计算过程中，接触类型采用面与面自动接触，接触算法采用对称罚函数算法，详细建模步骤参考文献[35]。图5所示为冰排抗压强度为2 MP时冰击力曲线。

图5 冰击时程力Fig.5 The ice impact loads

3.3 DVA最优参数设计和最佳安装位置

考虑到流冰撞击的最不利工况，将计算得到的冰击时程力以外荷载的形式加在所有的桥墩上，撞击位置为距墩顶10 m处，计算冰击荷载作用下桥梁结构的动力学响应。图6所示为冰击荷载作用下桥梁第三跨跨中和2号墩顶横向位移时程曲线和功率谱密度曲线。

由图6可知，冰击荷载作用下，桥梁跨中和墩顶横向位移急剧增大，冰击荷载的主频和桥梁结构二阶横向振动模态接近，可能激起此阶频段附近更大的振动，因此本文以桥梁二阶模态为控制对象，设计DVA的最佳参数。由图4可知，桥梁二阶横向振动墩顶位移最大，因此DVA安装在墩顶处，每个墩顶安装一个DVA。表1为质量比μ=0.1时，DVA的最佳刚度和阻尼。

图6 桥梁结构横向位移Fig.6 Lateral displacement of the bridge

表1 DVA最优参数Tab.1 Optimal parameters of DVA

3.4 DVA减振特性分析

基于上述DVA的最优参数设计，分析墩顶安装DVA对冰击荷载作用下桥梁跨中和墩顶横向位移的影响。图7所示为两种工况下(有DVA和无DVA)桥梁第三跨跨中和2号墩顶横向位移在时域和频域的响应。

当墩顶附加DVA 后，桥梁受到撞击产生的能量通过弹簧-阻尼力元传递给DVA，这一过程使能量得到耗散，桥梁结构横向位移显著减小，其中跨中和墩顶横向位移分别下降约48.6%和35.3%。由图7(b)可知，当桥梁不附加DVA时，由冰击荷载引起的桥梁跨中和墩顶横向位移在桥梁固有频率4.97 Hz附近出现较大的峰值；而附加DVA后，桥梁在此频段的横向位移显著降低，表明DVA能有效抑制冰击荷载作用下桥梁结构的横向振动。

图7 桥梁跨中和墩顶横向位移曲线Fig.7 The lateral displacement of the bridge mid-span and the top of the pier

4 冰撞作用下墩顶附加DVA对列车走行性的影响

采用前述的列车-轨道-桥梁-冰击动力学模型，列车采用8节车编组，轨道不平顺采用德国高干扰谱，波长1～45 m，考虑到流冰撞击桥墩的最不利情况，当列车行驶到桥梁第三跨时，流冰同时撞击所有桥墩，撞击位置为距墩顶10 m处。

4.1 行车速度对冰击作用下列车动力学响应的影响

为了研究DVA对不同行车速度下车辆动力学响应的影响，本文控制DVA质量比μ=0.1，行车速度为160 km/h，200 km/h，计算分析不同时速下车辆的动力学响应。图8所示为不同时速下车辆动力学响应峰值，图9为车体横向振动加速度谱密度曲线，图10为DVA对车辆振动的减振率。

图8 不同时速下车辆动力学响应峰值Fig.8 Peak of train dynamic responses at different speeds

图9 不同时速下车体横向加速度谱密度曲线Fig.9 Power spectral density of lateral acceleration of car body at different speeds

图10 车辆动力学响应振动抑制效果Fig.10 Vibration suppression effect of train dynamic response

由图(8)可知，在冰击荷载作用下，随着行车速度的增加，车体横向振动加速度、轮轨横向力、脱轨系数和轮重减载率均增大；当桥上附加DVA后，车辆动力学响应均不同程度的减小。分析图9可知，DVA显著降低了车体横向振动加速度在低阶频段的振动；由图10不难发现，行车速度为200 km/h时，DVA对流冰撞击作用下的车辆动力学响应的减振效果总是大于行车速度为160 km/h时的结果，表明DVA对列车振动有较好的抑制作用。

4.2 DVA质量比对列车动力学指标的影响

本节研究了DVA质量比对流冰撞击作用下列车动力学响应的影响。选取列车时速为160 km/h，DVA的质量比分别取0.05，0.10，0.15。图11为不同质量比DVA对车辆动力响应的影响和车体振动加速度谱密度曲线。

图11 不同质量比DVA时车辆动力学响应抑制效果Fig.11 Vibration suppression effect of train dynamic response under different mass ratio of DVA

由图可知，随着DVA质量比的增加，车体横向振动加速度、横向轮轨力、脱轨系数和轮重减载率的减振效果均增大；当桥墩顶附加DVA后，车体横向振动加速度在低阶频段内的振动得到了明显的抑制，但随着DVA质量比的增加，振动抑制增加的效果随之减小，表明在满足工程需求的前提下，不必刻意增大DVA质量比。

5 结 论

本文基于列车-轨道-桥梁动力相互作用理论和DVA设计方法，建立了冰击荷载作用下列车-轨道-桥梁-DVA动力学模型，探讨了DVA的最优参数和最佳安装位置，研究了冰击荷载作用下DVA对桥梁结构的减振特性和车辆动力学响应的抑振效果，得出以下结论：

(1) 冰击荷载作用下桥梁跨中和墩顶横向位移急剧增大，桥梁跨中和墩顶横向位移主频与冰击荷载主频一致，且接近桥梁二阶横向振动频率，这可能会激起桥梁结构在此阶频段更大的振动。

(2) 桥上安装DVA后，有效抑制了流冰撞击作用下桥梁结构的横向振动，在本文算例条件下跨中和墩顶横向位移分别下降约48.6%和35.3%，且在DVA作用下显著降低了桥梁结构横向位移主频峰值。

(3) 在DVA作用下，列车过桥时的车体横向振动加速度、横向轮轨力、脱轨系数和轮重减载率等动力学指标均明显减小；随着车速的增加，除横向轮轨力外，DVA对列车其他动力学指标的减振效果均增大；保持行车速度不变，列车动力学指标的减振率均随着DVA质量比的增加而增大。