不同长径比柱形装药水下爆炸冲击波演化规律

马 腾， 王金相， 刘亮涛， 黄瑞源， 唐 奎， 林尚剑， 顾阳晨

(南京理工大学 瞬态物理国家重点实验室，南京 210094)

近年来我国的海上军事力量不断的革新，水中兵器也在向高效毁伤、精确打击的方向发展。水中兵器对目标的毁伤效果最终体现在战斗部的毁伤威力上，而装药结构是实现水下战斗部高效毁伤的重要因素，因此开展研究药柱的形状对冲击波载荷特性的影响对毁伤模式的评估有重要意义[1-2]。对于球型装药，采用库尔[3]提出的经典经验公式可很好的预估冲击波压力等相关量的大小，但对于柱形装药却没有相应的经验公式，因此相关学者在球型经验公式的基础上，通过试验与数值的方法对柱形装药远场水下爆炸的经验公式做出了修正[4-7]。除此之外，相关学者还分析了药柱形状对近、远场冲击波载荷特性的影响。在试验方面，赵继波等[8]用锰铜压力传感器测量了冲击波的初始压力，并通过试验与数值模拟相结合的方法得到了近场TNT药柱轴向压力遵循指数衰减规律的结论；昝文涛等[9]通过试验与数值模拟相结合的方法，研究了等药量情况下药柱水下爆炸径向压力的衰减规律，得到了峰值压力随爆距的衰减曲线与方程；陈恒东[10]通过水下爆炸法测试了不同长度的导爆索在水下爆炸时，产生的峰值压力、冲击波衰减时间并计算了不同长度导爆索水下爆炸的比冲击波能、比气泡能和总能量，得出了比冲击波能和炸药爆炸的总能量先随着装药长度的增加而增大，当长径比为15时，比冲击波能达到最大，随后开始下降的结论。在数值模拟方面，邓贵德等[11]通过LS-DYNA数值模拟比较了球型与长径比为1的药包中心起爆后的冲击波峰值压力，得出了柱形炸药近场爆炸波呈现十字分布的结论；Sternberg[12]定义有效能量为动能加内能减冲击波传播过程的热能，通过拉格朗日法得到了不同长径比在15倍无量纲爆距处的有效能量，得出有效能量与方向角之间存在函数关系的结论；刘磊等[13]通过LS-DYNA数值模拟的方法比较了不同长径比的柱形装药对远场不同方向的冲击波峰压的影响，得到了等药量球形药包与柱形药包之间的映射关系。上述研究由于在试验上很难测得炸药近场完整的冲击波压力时程曲线，在数值方法上引入人工黏性系数处理强间断压力面时，黏性系数的取值对计算结果的影响很大，同时很难用一个状态方程同时描述炸药近场、远场水的压缩态，导致药柱形状的改变对近场冲击波相关参量的描述还存在诸多不足。

本文针对圆柱形装药分析长径比对水下爆炸冲击波演化规律的影响。理论上，基于圆柱炸药回转体的几何特性建立了柱形药柱中心起爆的二维模型，推导出初始冲击波压力的计算方法。利用AUTODYN仿真软件，数值模拟了不同长径比的圆柱炸药在无限水域中心起爆全过程，得到了初始冲击波压力值与冲击波压力时程曲线。开展了水下爆炸试验，验证了理论模型和数值模拟的有效性。结合理论分析、数值仿真和试验结果分析讨论了装药长径比对水下爆炸冲击波演化的影响。

1 圆柱形装药水下爆炸初始冲击波压力的计算方法

水下爆炸时，冲击波依次经历了爆轰过程、爆轰波与水界面的透射反射过程以及水中的传播过程最终到达空间任意位置。其中，爆轰波在炸药与水界面透射反射后，在界面上形成透射进入水域的初始冲击波。因此在计算初始冲击波压力时，需要分析炸药爆轰的爆轰现象以及波在炸药与水界面上的透射和反射过程。

1.1 爆轰过程分析

设炸药爆轰过程为理想爆轰，爆轰波传播过程为等熵过程。则爆轰波C-J面在到达圆柱炸药边界时产物[14]有如下关系

(1)

(2)

(3)

(4)

式中：pj，ρj，uj，cj分别为爆轰波的C-J压力、密度、质点速度和声速。当炸药为压装TNT时：D为爆速，取6 930 m/s；ρ0为炸药装药的初始密度，取1 630 kg/m3；k为等熵指数，取3。

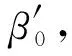
根据界面几何关系，入射波波阵面与炸药边界切线方向的夹角由下式计算

(5)

(6)

式中，t为爆轰波在炸药中的传播时间。

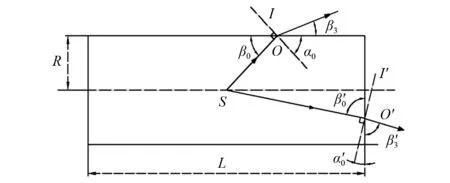
图1 柱形炸药初始冲击波压力计算模型Fig.1 Calculation model of initial shock wave pressure by cylindrical charge

1.2 爆轰波在炸药与水界面的透射、反射

当爆轰波到达炸药与水的界面时，波发生的透射、反射现象，如图2所示。图2中：OF界面为炸药与水介质的界面；OI为爆轰波阵面；OR为反射波阵面；OT为透射波阵面。未受扰动的界面OT在爆轰波的作用后，将发生转折，变成OF′，炸药与水的边界随着O点的运动变化。由于炸药的波阻抗大于水的波阻抗，因此反射波OR为稀疏波。若忽略掉反射稀疏波的不均匀性，水与炸药的界面与波阵面将流场分为五个区域：“(0)”区为炸药中爆轰波未扰动区；“(0′)”区为水中透射波未扰动区；“(1)”区为爆轰波入射后，稀疏波的波前区；“(2)”区为稀疏波波后区；“(3)”区为透射波波后区。受扰动后的界面OF′将“(2)”、“(3)”两区分开。

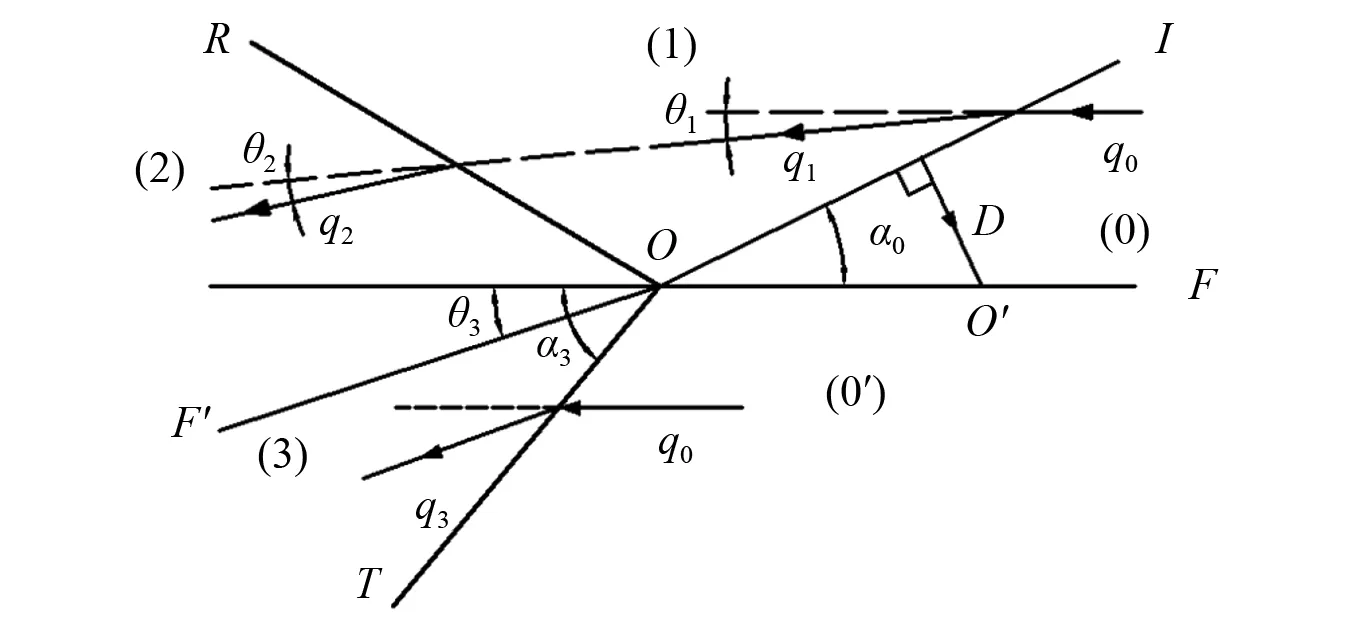
图2 炸药与水交界面示意图Fig.2 Interface between explosives and water

设欧拉坐标系中波后流团速度为u，拉格朗日坐标系中波后流团速度为q，则图2中qi就有

qi=ui+q0

(7)

根据几何关系与矢量关系，得到

(8)

(9)

(10)

式中，θ1为q0与q1之间的夹角。

1.2.1 爆轰波的反射

设爆轰波的强度不受反射稀疏波的影响，则图2中的“(1)”区入射波波速为炸药的爆速D，入射波扰动后流体微团速度u1，压力为p1，密度为ρ1。在图2中由q0向q1逆时针旋转时，角度取正值。故C+特征线为贯穿特征线[15]，在此简单波上有

(11)

式中，M为马赫数。

同时，在反射波阵面上同样满足伯努利方程，则

(12)

由于爆轰波在界面上的反射过程可认为是等熵过程，则反射波波阵面两侧压力、密度、声速的关系有

(13)

(14)

式中：ρ2为“ (2)”区中反射波扰动后炸药的密度；p2为压力；θ2为q1与q2之间的夹角；k1为多方气体的等熵指数，取1.4。

1.2.2 爆轰波的透射

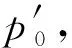
(15)

透射波区“(3)”的折射波极曲线可由式(16)计算

(16)

当水为压缩态时，可引入水的多项式状态方程，则有

(17)

(18)

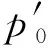
1.2.3 界面上的定解条件与求解过程

根据图2可知，炸药介质中反射波扰动区“(2)”与水介质中透射波扰动区“(3)”之间属于接触面间断，故在界面OF′上满足下面三个定解条件

q2∥q3∥OF′

(19)

p2=p3

(20)

η=θ3-(θ1+θ2)=0

(21)

结合1.2.1节和1.2.2节可知，求解炸药与水界面上的初始压力，即求式(11)与式(16)所代表的反射与透射极曲线的交点(θ3，p3)。根据反射波阵面与透射波阵面上的连续性假设、动量守恒条件，联立式(10)、式(11)、式(16)得式(22)。在求解时采用迭代法，最终使式(22)满足式(19)、式(20)、式(21)。

(22)

表1 水多项式状态方程参数

2 圆柱形装药水下爆炸试验

图3为试验布置原理图，图4为水下局部放大实物图。本试验在长2 m、宽2 m、高2.3 m、厚0.1 m的水箱中进行，水深2 m。将三个自由场水压传感器一端系在钢架上，一端用重物垂在水中B、C、D三个位置；将炸药用同样的方式垂于A点，使A、B、C、D四个点同处于水深1 m的位置，其中B、C、D三个传感器测点距炸药A点分别为50 cm，60 cm，70 cm。

图5为试验用炸药，其尺寸如表2所示。试验中采用PCB-W138A05型自由场压力传感器，数据采集系统如图6所示。为防止测量时出现“漏峰”现象，试验采样频率为2 MHz。试验前采用长径比为1 ∶1的10 g TNT圆柱药柱标定位于B、C、D测点的三个传感器，分别得到其灵敏度为141.8 mV/MPa，142.7 mV/MPa，143.3 mV/MPa。

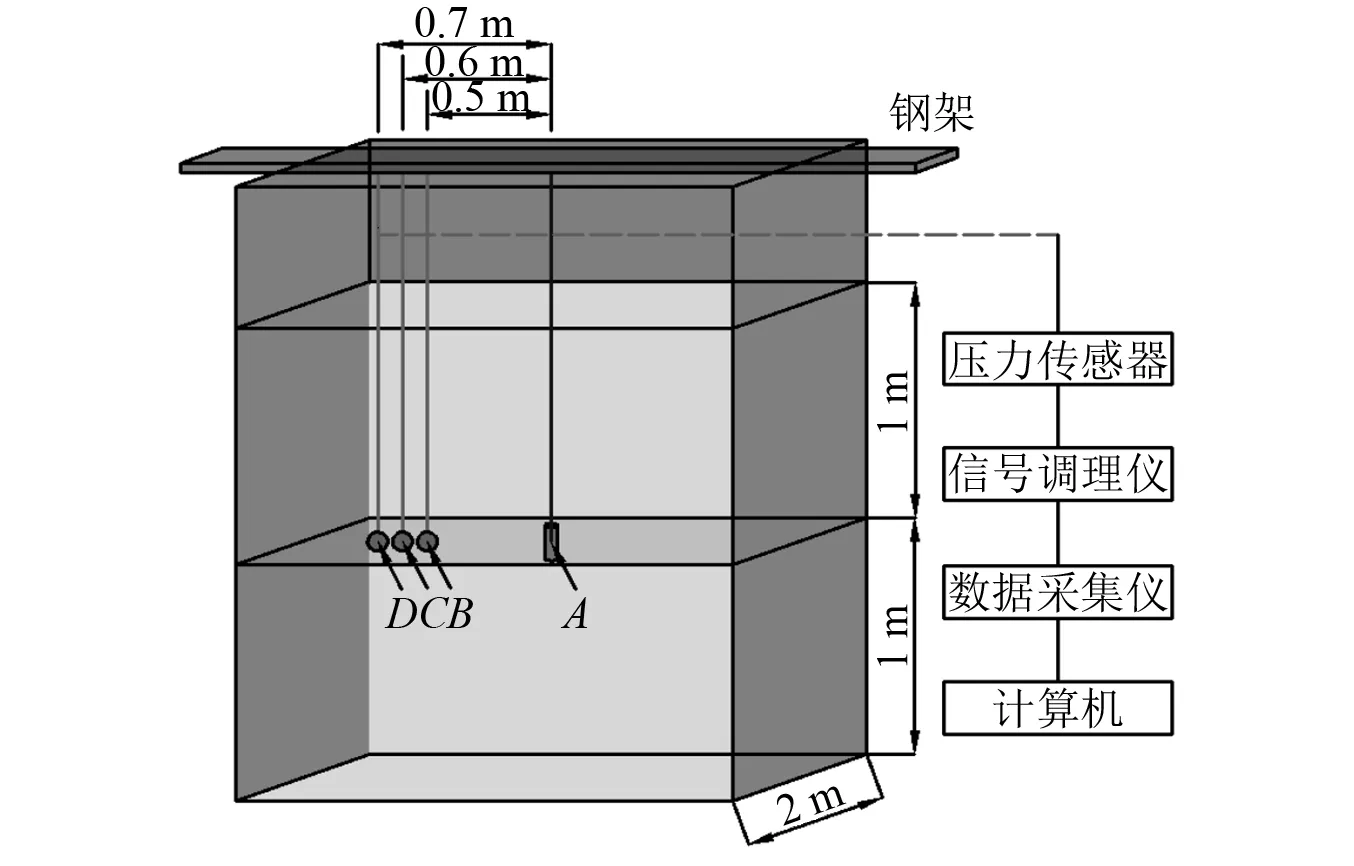
图3 试验布置原理图Fig.3 Schematic diagram of the experimental

表2 试验用药尺寸

图4 水下局部放大实物图Fig.4 Photo of underwater experiments enlargement

图5 10 g TNT圆柱药柱实物图Fig.5 10 g TNT cylindrical charge

图6 试验数据采集系统图Fig.6 Experimental data acquisition system

3 圆柱药柱水下爆炸的数值模拟

由于试验中存在场地限制，传感器数量、量程限制等，仅能得到炸药径向的冲击波压力数据。为分析药柱形状对冲击波演化的影响，进一步通过数值模拟补充计算相关测点的数据。

3.1 计算模型

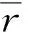
图7 圆柱炸药水下爆炸数值计算模型Fig.7 Numerical calculation model of cylindrical charge for underwater explosion

表3 10 g TNT装药数值计算模型尺寸

3.2 状态方程及其参数

3.2.1 水的多项式状态方程

水的多项式状态方程根据压缩度的不同具有不同的形式。当水被压缩时(μ≥0)，状态方程见式(17)。

当水被拉伸时(μ<0)，状态方程为

P=T1μ+T2μ2+B0ρ0EM

(23)

当水处于既不压缩也不膨胀时(μ=0)，式(23)可以简化为统一形式

P=B0ρ0EM

(24)

设药柱未在水中起爆时，无限介质水域均处于既不压缩也不膨胀状态，因此该处的初始压力为静水压。

P=PH=P0+ρgh

(25)

式中：p0为大气压力；h为水深；g为重力加速度；EM为单位质量内能增量；A1，A2，A3，T1，T2为压强量纲常数；B0，B1为无量纲常数。具体参数见表1。将式(24)、式(25)式联立即可得到1 m水深处对应的EM为396.79 J/kg。

3.2.2 炸药状态方程

炸药采用JWL状态方程

(26)

式中：P为反应物的压力；V为相对体积；E为单位体积内炸药内能；ω，A，B，R1，R2为表征炸药特性的常数,具体参数如表4所示。

4 分析与讨论

4.1 试验结果分析

通过等质量圆柱形装药水下爆炸试验，本文得到了径向方向爆距为50 cm，60 cm，70 cm处的压力时程曲线。对比图8中三幅图，长径比由1∶1增大到2.6 ∶1，并未出现明显的衰减速率变化，这表明在远场，改变长径比对时间衰减常数的影响很小。同时在曲线的下降沿均出现了“M”型波，是由水箱的壁面反射和传感器外表面局部空化的综合作用引起的。

长径比对远场冲击波峰值压力的影响，如表5所示。表5中列出了长径比为1∶1的#1峰值压力试验结果与P.Cole理论值的误差，并得到了径向方向三个爆距位置处长径比与峰值压力的关系。试验结果表明：#1试验结果与P.cole经验公式误差小于1.28%，验证了试验数据的准确性；当圆柱炸药当量不变时，将长径比由1∶1增大至2.6 ∶1，可提高径向方向的冲击波峰值压力。

表4 AUTODYN程序提供的炸药材料模型参数

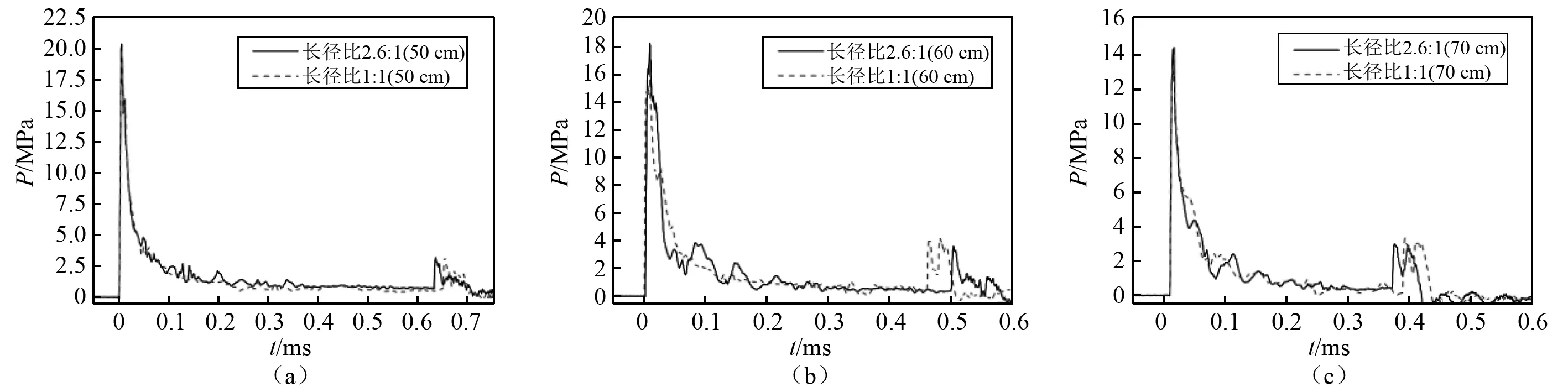
图8 圆柱形装药水下爆炸试验的压力时程曲线图Fig.8 Pressure-time curve of cylindrical charge underwater explosion experiment

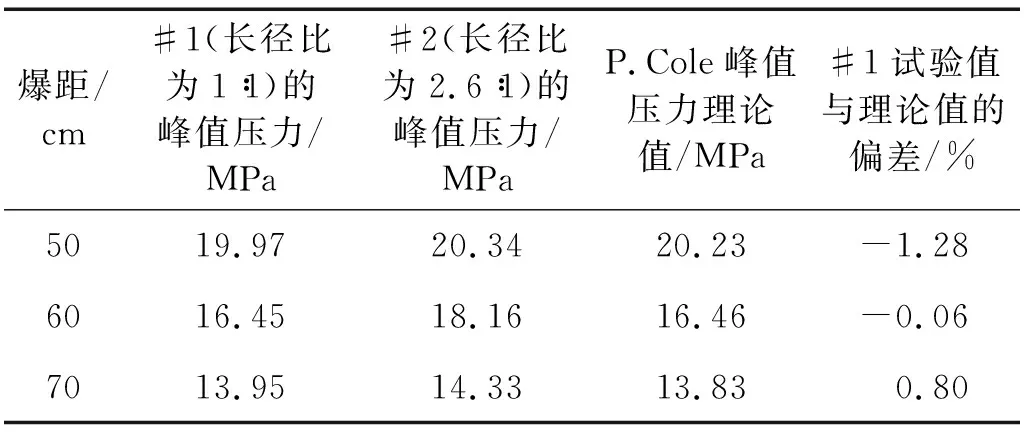
表5 长径比对远场冲击波峰值压力的影响

4.2 数值模拟有效性分析

4.2.1 网格敏感性分析

为避免网格数量对数值模拟结果的影响，本文对比了网格大小n分别为0.75 mm，1 mm，1.25 mm，1.5 mm的数值模拟结果，并输出爆距为70 cm处的冲击波压力时程曲线,如图9所示。图9中曲线表明，当网格大小n从1.25 mm细化到0.75 mm时，其对冲击波峰值压力的影响很小，因此当网格大小为1 mm时计算结果已经收敛。

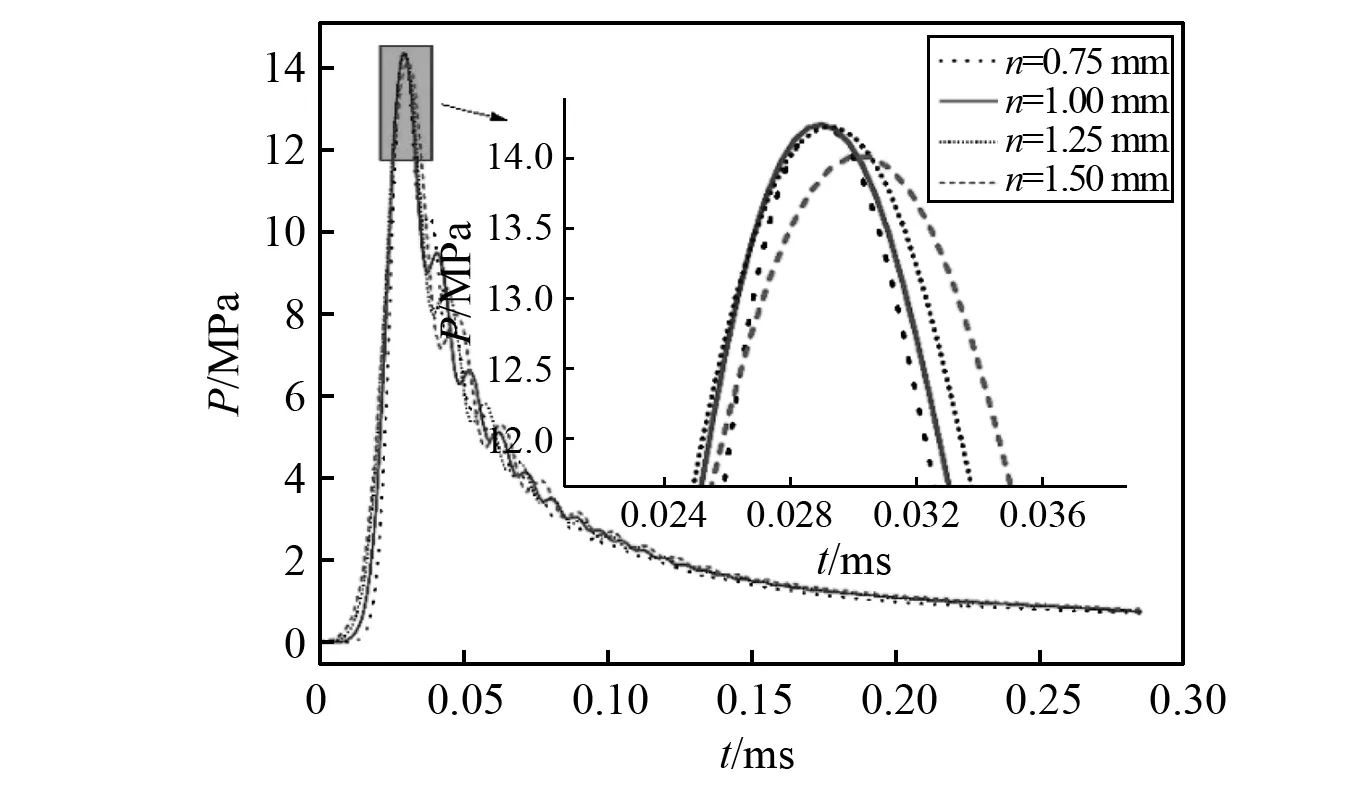
图9 网格敏感性分析图Fig.9 Sensitivity analysis of grid size

4.2.2 远场冲击波数值模拟有效性分析

本节以冲击波峰值压力为标准，对比了长径比为1 ∶1的10 g TNT炸药水下爆炸试验值与2D-AUTODYN数值模拟结果。压力时程曲线对比如图10所示，数值模拟得到的压力时程曲线与试验曲线整体吻合的较好，具有相当的指数型衰减速率。表6中峰值压力数据表明，数值模拟得到的峰值压力数据与试验数据具有良好的一致性，误差在2.2%以内。

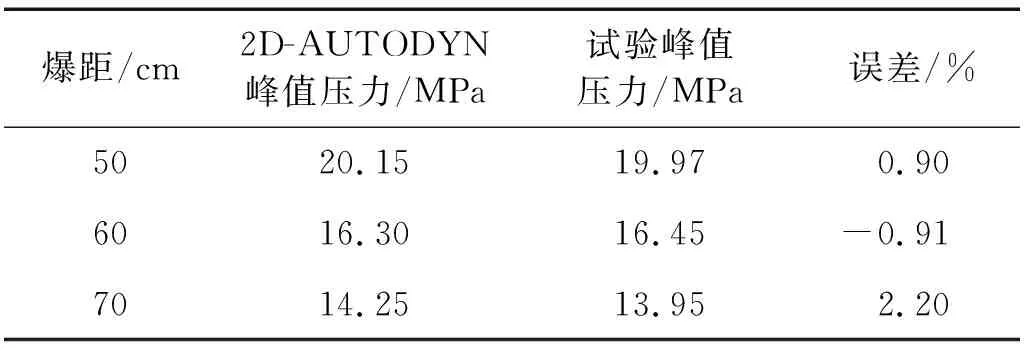
表6 水下爆炸试验与数值模拟峰值压力

4.2.3 近场冲击波数值模拟有效性分析

在水下爆炸时，由于近场冲击波的压力很难由试验测准，且柱形药柱的冲击波峰值压力没有准确的经验公式，故本节在验证了远场(无量纲爆距40～60)数值模拟有效性的基础上，计算了长径比为3 ∶1的10 g圆柱TNT的初始冲击波压力理论值，并对比了数值模拟结果，如图10、图11以及表7所示。其中，圆柱面的初始压力最大误差为9.17%，端面的初始压力最大误差为1.8%。该结果进一步验证了第三章中相关参数的准确性，同时印证了初始冲击波压力求解方法的准确性以及相关假设的合理性。

4.3 药柱形状对近场冲击波传播过程的影响

当爆炸距离距炸药足够远时，炸药可简化为质点模型，其形状系数对冲击波传播过程的影响可以忽略不计。因此本节以长径比为3 ∶1的圆柱药柱为例，重点分析大长径比柱形药柱近场冲击波传播过程中波阵面的演化过程、波阵面上高压区的转移过程以及典型轴、径向冲击波的衰减规律。

通过数值模拟得到长径比为3 ∶1的圆柱炸药起爆后，不同时刻近场冲击波的压力云图，如图11所示。图11(a)时刻为炸药爆轰完全的时刻，其冲击波的波阵面在圆柱面趋向于椭圆型，在端面趋向于方形。波阵面上轴向的冲击波压力远大于径向的冲击波压力。在该时刻冲击波压力的方位差异性可用理论模型解释：假设炸药内部爆轰波在传播时是等熵过程，即爆轰波在炸药内以C-J爆速传播。炸药中心起爆后，爆轰波先在圆柱面透射，后在圆柱端面透射。炸药起爆3.5 μs时，炸药径向的冲击波已经在水介质中传播并衰减了一段时间，而轴向冲击波刚开始在水中传播，该时刻出现轴向冲击波压力远大于径向压力的现象。

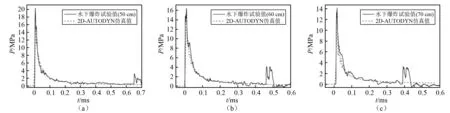
图10 水下爆炸试验与数值模拟的压力时程曲线对比图Fig.10 Pressure-time curve between underwater explosion experiment and numerical simulation

表7 冲击波初始压力理论模型计算值与仿真结果的对比

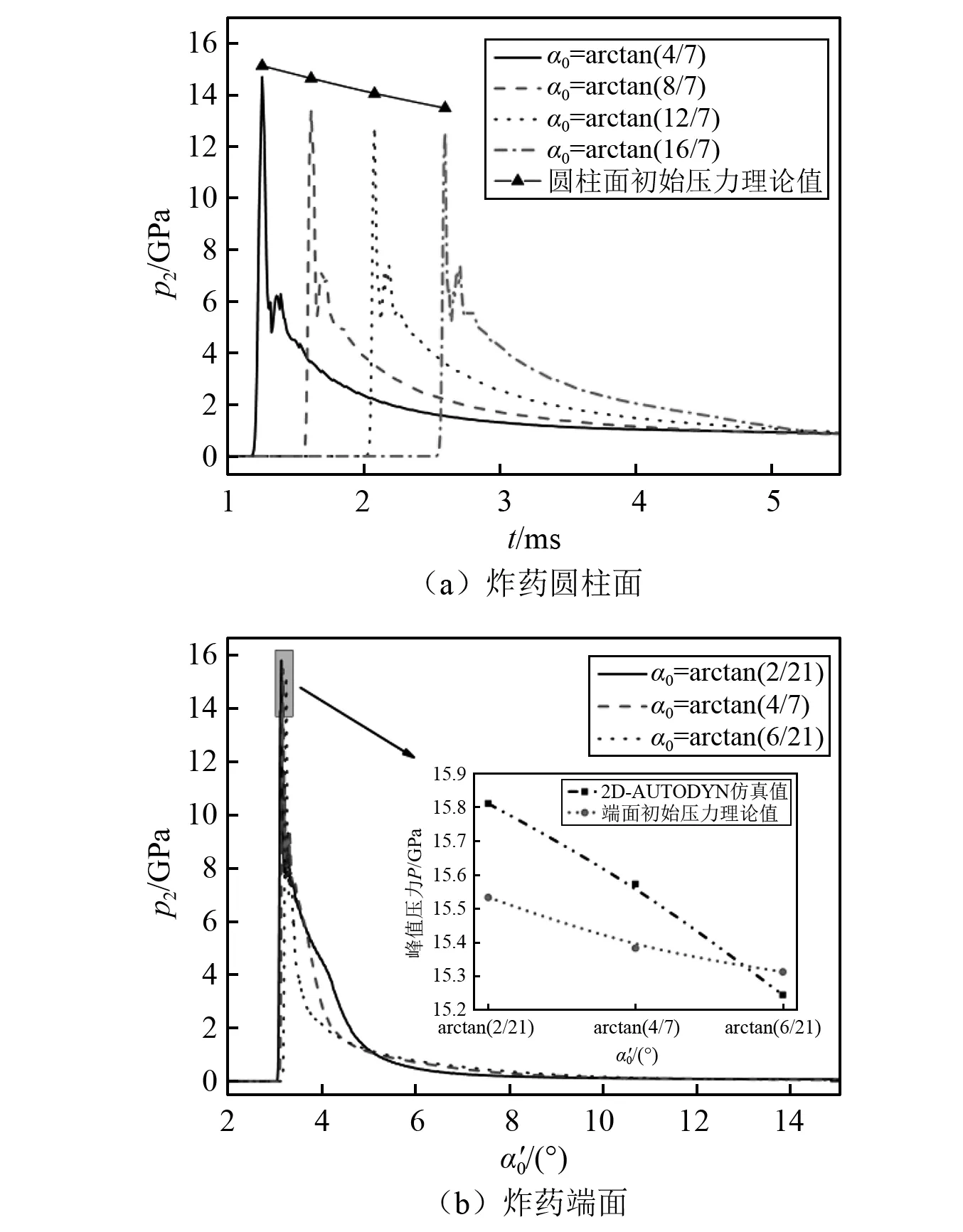
图11 初始压力理论值与数值模拟结果对比图Fig.11 Comparison of theoretical and numerical results of initial pressure

图12 圆柱炸药近场冲击波传播规律Fig.12 Near-field shock wave propagation of cylindrical charge

由图12(a)～图12(d)时刻压力云图可知，随着冲击波分别到达无量纲爆距为2.0、2.9、3.5、4.2处，冲击波波阵面逐渐从柱形趋向椭球型，高压区也从轴向趋向为四周等压再趋向径向，这表明大长径比的圆柱装药形成的冲击波在传播过程中，各个方向的衰减速度有所差异。为进一步探究大长径比对衰减速度的影响，选取轴、径向为典型方向，分别得到爆距在25～50 mm的压力时程曲线，如图13所示。比较图13(a)、图13(b)的曲线，轴向冲击波到达同一爆距的时刻早于径向，因此大长径比的圆柱装药轴向冲击波压力随时间的衰减速度大于径向的衰减速度。

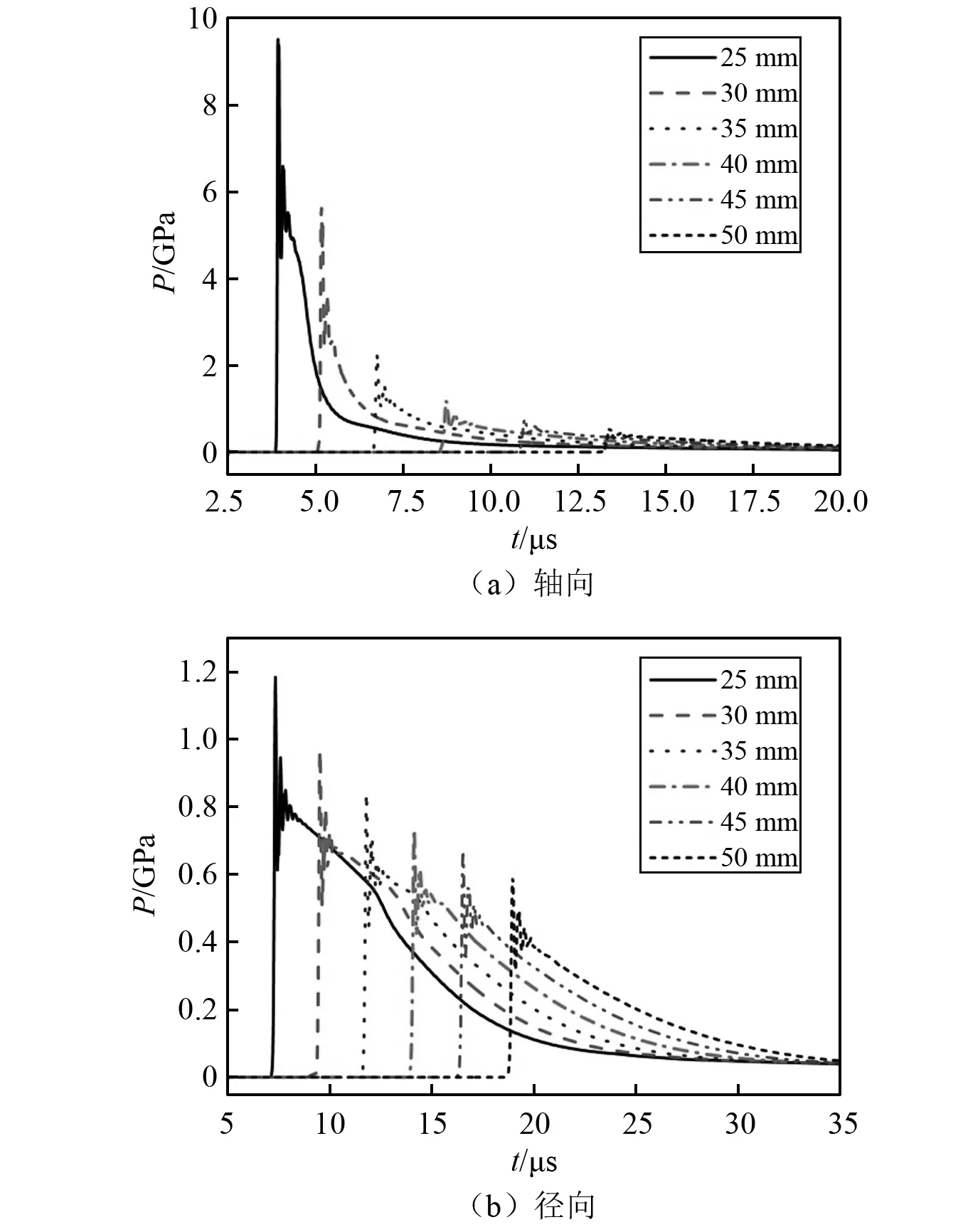
图13 长径比为3 ∶1的圆柱炸药近场冲击波压力时称曲线Fig.13 Near-field shock wave pressure of cylindrical charge with length-diameter ratio of 3 ∶1

4.4 药柱长径比对冲击波压力分布的影响

不同长径比的圆柱炸药，在水下中心起爆后0.05 ms时刻的压力云图，如图14所示。图14(a)～图14(f)的变化规律表明，圆柱炸药的形状会影响起爆后冲击波在水中的波阵面形状以及压力的分布情况。长径比由1 ∶1增大到10 ∶1，波阵面的形状呈长轴增大，短轴减小的椭圆型(焦点在径向)。冲击波压力随着长径比的增大逐渐向径向汇聚；当长径比由1 ∶1减小到2 ∶1，波阵面的形状同样呈长轴增大，短轴减小的椭圆型(焦点在轴向)，冲击波压力随着长径比的减小逐渐向轴向汇聚。

为量化长径比对不同空间位置处冲击波压力的影响，以长径比为1的峰值压力P1为标准，得到无量纲爆距R/R0在10、20位置处，长径比在1 ∶1～5 ∶1内峰值压力比值P/P1与图1中方向角β0的关系，如图15所示。图15中：R为爆距；R0为等质量球型炸药的球径。由图15(a)可知，峰值压力与角度的变化呈单调趋势，这表明冲击波到达10倍无量纲爆距时，长径比改变引起的高压区转移过程已经结束。当长径比大于1 ∶1，冲击波峰值压力随着方向角的增大而单调增长；当长径比小于1 ∶1，冲击波峰值压力随着方向角β0的增大而减小。

图14 不同长径比的圆柱炸药近场冲击波压力云图Fig.14 Near-field shock wave pressure contour of cylindrical charge with different slender ratios

对比图15(a)、图15(b)两幅图，以长径比为3 ∶1的轴向(方向角为0°)方向为例，当冲击波由无量纲爆距10传播到无量纲爆距20时，压力的比值降低了8%，而同一爆距处的方向角β0由0°增大到45°，压力比值的差减小。这表明在冲击波传播过程中，长径比大于1 ∶1的柱形炸药轴向的近场冲击波压力衰减速率始终大于其他方向；当长径比小于1 ∶1时，径向冲击波压力衰减速率始终大于其他方向。同样的，以长径比为3 ∶1的径向方向为例，当冲击波由无量纲爆距10传播至20时，压力的比值从120%下降为110%，表明随着冲击波的传播，药柱形状对压力分布的影响在逐渐降低。因此在1 ∶1～5 ∶1的长径比和20倍无量纲爆距范围内，增大药柱长径比可定向增强炸药径向的冲击波压力，但药柱的形状对冲击波压力分布影响随着爆距增大而减小。

5 结 论

通过本文的研究，可以得出以下结论：

(1)本文根据圆柱形炸药回转体的特性，建立了二维轴对称模型，通过分析炸药中心起爆的爆轰过程以及爆轰波在炸药与水边界上的透射反射过程，得到炸药界面上的初始压力以及传播方向的计算方法。

(2)圆柱形装药水下爆炸后，随着冲击波在水中传播，冲击波波阵面逐渐从柱形趋向椭球型再趋向球型，当冲击波传播至10倍无量纲爆距时高压区的转移结束。

(3)当长径比大于1 ∶1时，炸药轴向的冲击波压力衰减速率大于径向的衰减速率，冲击波峰值压力随着方向角的增大而单调增长。

(4)在1 ∶1～5 ∶1的长径比和20倍无量纲爆距范围内，增大药柱长径比可定向增强炸药径向的冲击波压力，药柱的形状对冲击波压力分布影响随着爆距增大而减小。