集中载荷作用截面的应力分析研究
王子豪,舒香澍
(南京航空航天大学航空学院,江苏 南京 210000)
集中载荷的概念广泛应用于刚体力学、梁板壳等理论,在弹性理论中也有应用。但我们知道,在线弹性理论下的空间问题或平面问题中,有限的集中力将在作用点附近产生无限大的应力和位移。这个解明显地与它的前提小变形矛盾。
材料力学教材中,将集中力等效为作用面积远小于构件尺寸的分布载荷处理,并得出在集中载荷作用两侧内力发生突变的结果,但并未给出该截面内力的准确值。本文将这种等效的分布载荷视为作用于两侧截面的“分布载荷”,这是因为在每一侧该“分布载荷”作用范围为无穷小、平均载荷集度为无穷大,而分布载荷在此作用范围的积分为有限值,不妨将该“分布载荷”视为作用于两侧截面的集中力分析。
1 一个重要的反思
引例:简支梁中点处作用一集中力(图1),如何求解集中力作用处的内力(剪力)?

图1
在工程上,集中力是作用面积远小于构件尺寸的分布载荷,因此,对于此例,建立自右向左的x轴,并给出分布载荷集度函数。
同时注意到简支梁的结构、载荷都关于集中力对称,从而梁的内力、变形都会关于集中力对称。因此,可以认为等效分布载荷也关于集中力对称。
于是,利用力的简化定理,向集中力作用处横截面简化,不难解出剪力等于零的答案。
在理想情况下,取梁上任意横截面(除集中力作用处)求得剪力大小为。若将集中力等效为作用面积远小于构件尺寸的分布载荷,那么,无论将分布载荷作用范围缩小到何种程度,在此作用范围内梁的横截面上的剪力仍然会受到分布载荷的作用而改变,从而导致在此范围内的变形发生改变,这是不允许的,因为由以下讨论可知,在分析集中力作用处剪力大小的过程中,梁在集中力附近微段的变形是决定剪力大小的重要因素,不相等的变形,势必会导致分析结果的错误。 同时,即便分布载荷作用范围极小,但其集度的平均值极大,依然会对梁的变形造成可观的影响,因此这种“等效”的差别是不可忽略的。所以归根结底,将集中力“等效”为作用范围足够小的分布载荷依然是停留在对分布载荷问题的讨论,并未过渡到集中力,这种等效并不成立!
另外,截面剪力一定等于突变处两侧剪力的平均值吗?上述结果求得的剪力为零一定是因为该结构和载荷的特殊性吗?
举个反例,假设集中力作用于简支梁的由三等分点(图2),那么,梁的变形不再关于集中力对称(这里的“对称”只考察距集中力范围内的情况),在这种非对称情况下,集中力所等效出的分布载荷完全可以不再限制于对称分布。于是,分别取均布载荷、形如直角三角形的分布载荷的情况研究(图2)。

图2
依上述求解过程,发现这两种分布载荷所对应的集中力作用处的剪力并不相同,前者取突变两侧的平均值,而后者会因为集中力两侧分布载荷的合力不相同而导致此处剪力不为平均值,所以第一个问题的答案是否定的。但是,集中力作用处横截面上的剪力是唯一的,因此集中力只能对应一类分布载荷,这类分布载荷与集中力满足合力方程,并且利用这些分布载荷求出的集中力作用处的剪力一定是唯一的。同时应注意到梁的变形已经确定,即这一类分布载荷中只有一个符合变形条件。
回到理想情况,如何分析上述的等效不成立问题?借由工程实际的启示,现欲寻求集中力的“分布载荷”,但是,此时的“分布载荷”必须满足两个条件,分别是力的外效应与内效应的等效,所谓外效应,即满足在刚体范畴下的力系的等效;所谓内效应,即力对梁的变形状况的等效。
2 求解思路
在此主要分析内效应的等效,即对任意无限接近集中力的横截面,都可以找到一分布载荷,使分布载荷的作用范围小于横截面与集中力的距离。在这种叙述方式下,可以保证各横截面的剪力大小都等于,但分布载荷的作用范围却在“运动”,呈现出不断变小、趋近于零的状态。
那么,这种“运动”意味着什么?因为我们所寻找的“分布载荷”会使所有的横截面都与等效前的状态一致,但是,以上的要求却断定我们无法找到通常意义上的分布载荷(即作用范围固定的分布载荷)。联系工程实际:集中力作用处剪力的唯一性会约束集中力所等效的分布载荷的选取,于是,我们推断:这种“分布载荷”是这些分布载荷中最特殊的一种。其特殊性表现为作用范围为集中力作用处的两侧截面(图3)。

图3
下面给出做出此推测的原因:将这一类分布载荷以及梁从集中力作用处截开,考虑截开后的左侧梁,再由第一个推测:无论理想还是实际,集中力作用处剪力是相等的,左侧梁的“分布载荷”分量与这一类分布载荷分量具有相同的外效应,从而得出“分布载荷”是其中之一的结论。其二,为保证与理想情况的变形情况(内效应)完全相同,“分布载荷”只能作用于两侧截面。
对于实际情况,已经由剪力的唯一性对集中力的分布载荷的选取进行了约束,但仍未考虑变形对这一类分布载荷的约束,并解出分布载荷。
对于理想情况,已经由剪力相同的推测导出理想集中力可等效为分别作用于两侧截面上的分力的结论,但仍未解出两个分量。
为便于利用已学的胡克定律进行解释,这里不再讨论剪力,而是引入一个类似的轴力问题(图4)。
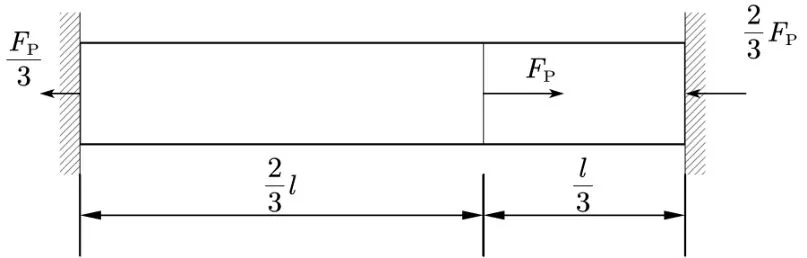
图4
其中,轴向集中力作用于杆件右三等分处。
由平衡方程、变形协调方程、胡克定律求解出两侧的约束力大小分别为。
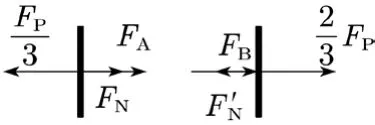
图5

3 结论
综上所述,对于集中载荷作用下的简支梁以及两端固定的细长杆,将杆件从作用截面截开,集中载荷等效为作用于两侧截面的集中力,这两个力分别与截开后两杆上的约束力平衡,所以截面内力为零。
4 应用
这个理论也为我们寻找分布载荷的集中力位置提供了理论依据:无论分布载荷的具体分布情况,集中力作用点的位置一定可以将两边分布载荷划分为两边合力大小相等。
但是,这个应用有较大的局限性。于有限大小的集中力,用线弹性理论求得的在集中力附近的应力场和位移场,肯定与实际情况相差甚远,不能应用,而在远离集中力的地方,线弹性理论解与实际情况相差不多。这时,集中力和与它相应的解可以在圣维南含义下近似应用。
其中比较值得注意的是,在刚体力学中,集中力偶属于集中载荷。定义是一对大小相等、方向相反的集中力。且在刚体力学理论,力偶是可以沿着平面平移而对结果不造成影响的矢量。在线弹性理论中,力偶如果继续能够沿着平面平移,对应力场和位移场的结果分析会造成十分重大的影响。所以,应该放弃集中力偶而代之于集中力对的概念。
——超集中力
—— 梁在集中力作用点处的剪力分析

