含煤粉层的刨头-滑架体三维粗糙接触碰撞特性研究

张 瑜， 王 倩， 陈洪月， 毛 君

(1.安阳工学院 机械工程学院，河南 安阳 455000；2.安阳工学院 安阳市先进航空材料与加工技术重点实验室，河南 安阳 455000；3.辽宁工程技术大学 机械工程学院，辽宁 阜新 123000)

由于装配、加工误差、磨损以及保证相对运动的需要，机构连接运动副之间会存在一定的间隙，降低了机构的运行精度以及机构的稳定性，当间隙接触界面存在煤粉颗粒时，更会加剧接触载荷复杂化。刨煤机被广泛用于薄煤层开采煤壁，在链条牵引下刨头沿着中部槽上滑架体作往复直线运动进行截割煤壁。当刨头截割煤壁产生的煤粉附着在刨头与滑架体接触表面时，形成刨头-煤粉颗粒-滑架体三体间隙接触情况，在交变外载荷作用下，会产生较为复杂的接触碰撞动力学行为，因此研究含煤粉层的刨头-滑架体三维接触变边界、高瞬态的碰撞特性具有工程实际意义。

关于含间隙机构动力学国内外学者做了大量的工作[1-4]。如吴丹等[5]推导了含干摩擦弹性碰撞系统的黏着、滑动和碰撞运动判断条件，利用转换相图揭示了系统穿越分界面时产生的簇发振荡行为；钱震杰等[6]基于高次刚柔耦合理论和Lagrange乘子法，研究了柔性多体含间隙碰撞stick-slip过程的动力学特性；Bai等[7]提出了含有变刚度系数的混合接触力模型，用来描述间隙运动副元素的接触碰撞力。张艳龙等[8]通过引入Dankowicz动摩擦模型，研究了摩擦诱导因素对碰撞振动系统动力学特性的影响；郭嘉楠等[9]建立了考虑粗糙接触界面特性的碰撞力模型，研究了粗糙界面参数对碰撞力的影响。可见，表面形貌以及接触材料属性对接触力模型都具有一定的影响[10-11]。目前，Greenwood和Williamson提出了G-W微凸体接触模型，为粗糙表面间的接触模型奠定理论基础，在G-W模型基础上，学者们分别进行了相应的改进，如Carbone[12]提出改进模型允许微凸体尖端的曲率半径取决于微凸体的最大高度；肖会芳等[13]构建了整个粗糙界面的接触刚度，可满足接触面积连续、单调且光滑变化的条件；张伟等[14]基于G-W模型，提出了考虑微凸体基体以及微凸体相互作用的接触刚度模型，扩展了G-W模型的应用范围；Yuan等[15]考虑建模过程中的多尺度性，采用分形几何理论，建立了粗糙表面弹塑性接触模型。李玲等[16]利用赫兹接触理论建立了考虑硬涂层的粗糙表面微观接触模型；刘峰壁等[17]基于概率统计理论建立了粗糙界面弹性变形、塑性变形与第三体颗粒分布的关系；王超等[18]基于雷诺方程、黏度方程以及G-W模型，建立了含固体软颗粒作用的三体粗糙界面接触模型。

上述学者的成果为本的文研究提供了一定的理论指导，本文基于刨头-滑架体几何结构特点，提出了适合于刨头与滑架体的三维接触碰撞过程判定准则，综合考虑煤粉颗粒、表面形貌在刨头与滑架体间的界面影响，建立了刨头-滑架体三维接触碰撞动力学模型，采用数值分析方法结合试验测试研究了刨头-滑架体接触碰撞动态特性。

1 碰撞判断准则的确定

刨煤机刨头-滑架体机构主要由刨刀、刀座、刨头、滑架体组成，如图1所示。为了便于分析刨头-滑架体接触碰撞的判断准则，去除刨刀、刀座及其附属结构，简化成如图2所示模型。在此模型基础上，采用将三维多面体碰撞检测降维到二维多边形碰撞检测的方法，即刨头截面中各关键顶点投影到某一坐标平面中，随之采用点到直线或曲线的距离的检测方法进行判断滑架体各顶点是否与刨头产生几何重叠。

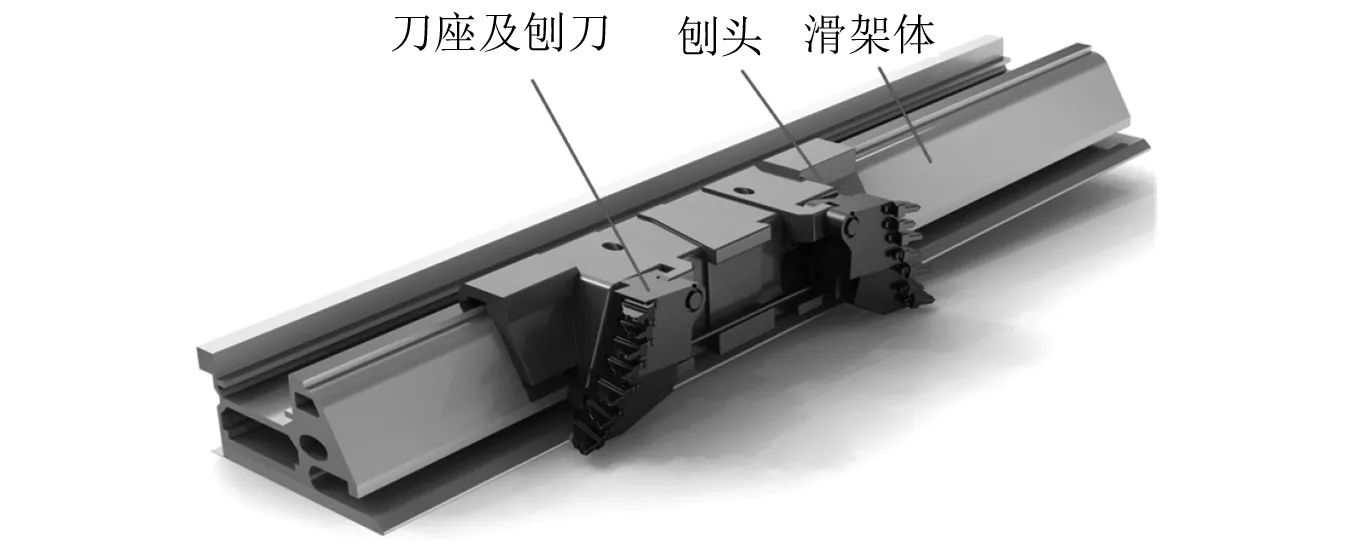
图1 刨头-滑架体的物理模型Fig.1 Physical model of plow head-sliding framework

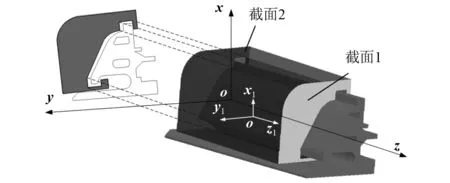
图2 空间相对位置简化图Fig.2 Simplified diagram of relative spatial position

以投影到xoy平面进行检测为例，如图2中将截面2投影到xoy平面中，投影后的截面转化为图3(a)形式，截面1按照同样的方法投影并转化为图3(b)形式。刨头各端顶点转化形式如下：设定刨头在运动初始时刻，各顶点的空间坐标值Ci为(x0i,y0i,z0i)，i=(1,2,…,6)，当各顶点绕三坐标轴旋转及平移之后各顶点坐标值Di为(x′j,y′j,z′j)，j=(1,2,…，6)，如图4所示，二者之间转化矩阵公式表示为

(1)

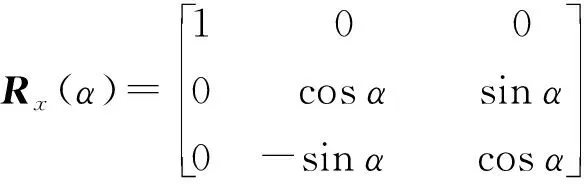
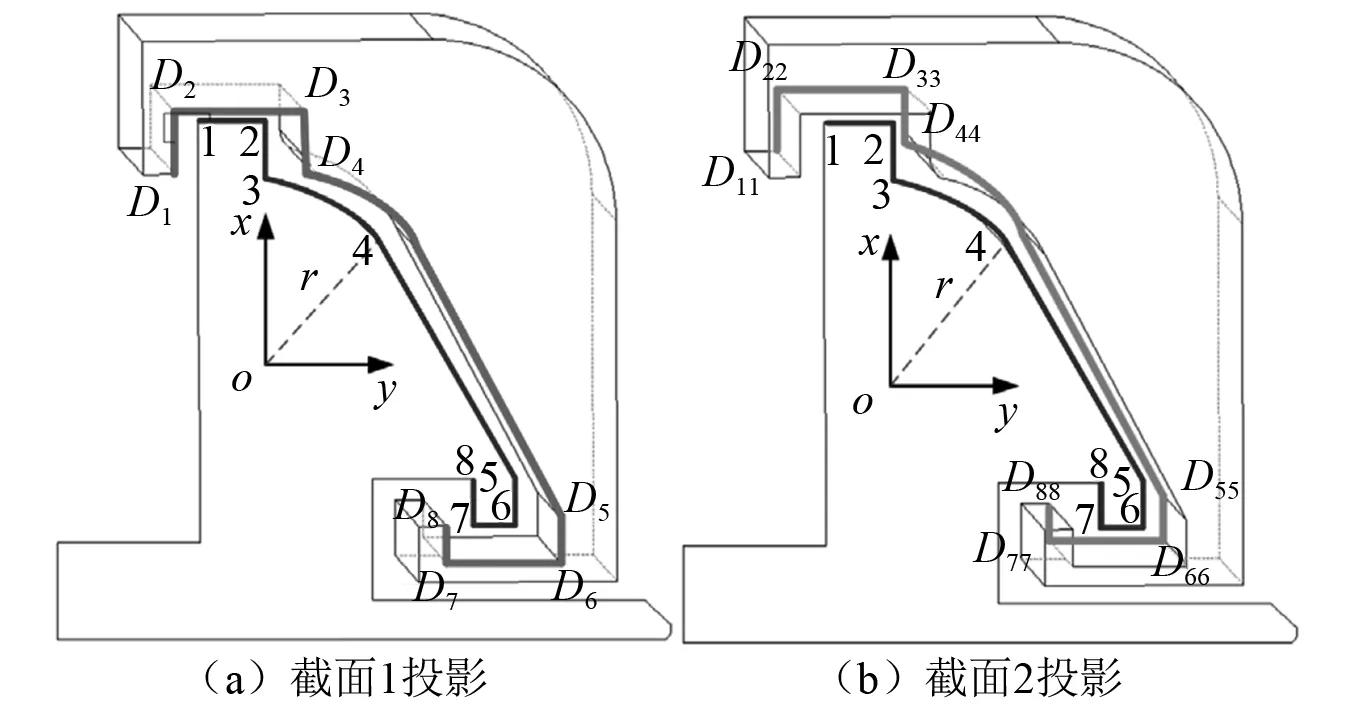
图3 截面投影图Fig.3 Cross-sectional projections

图4 空间坐标变换Fig.4 Transformation of spatial coordinates

根据式(1)计算顶点坐标Di，表示成式(2)～式(4)形式

x′j=x0icosβcosθ+y0icosβsinθ-sinβz0i+xp

(2)

y′j=x0i(-cosαsinθ+sinαsinβcosθ)+

y0i(cosβcosθ+sinαsinβsinθ)+

z0i(sinαcosβ)+yp

(3)

z′j=x0i(sinαsinθ+cosαsinβcosθ)+

y0i(-sinβcosθ+cosαsinβsinθ)+

z0i(cosαcosβ)+zp

(4)

当z′j=0时获得顶点Di在xoy平面投影后的坐标。最后，根据坐标平面内两点确定一条直线建立投影后刨头截面位置，并通过点到直线或曲线距离的算法(该算法本课题组已在文献[19]中进行了推导，此处不再赘述)逐一判断刨头与滑架体各顶点是否产生接触碰撞。此外，由于滑架体顶点3、4区间段是以半径为r的圆弧，只需判断D4(D44)点距离坐标原点的距离是否小于等于半径r，如果小于等于则产生碰撞，否则未碰撞。

2 接触力模型

接触碰撞力模型反映了系统接触动态性能，目前广泛采用Lankarani Nikaravesh模型

(5)

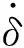
Lankarani Nikaravesh模型考虑了碰撞过程中的能量损失，但接触表面形貌以及接触面间的介质并未进行全面描述。为此，根据刨头、滑架体几何结构特点，考虑刨头-滑架体之间的表面粗糙度以及煤粉颗粒，将二者之间的接触分为刚性体-微凸体接触以及煤粉层-微凸体接触，滑架体定义为刚性体，刨头定义为柔性粗糙体。当刨头与滑架体底板、上滑面接触时采用煤粉层-微凸体接触力模型；当刨头与滑架体其他面接触时采用光滑刚性体-微凸体接触力模型。

2.1 刚性体-微凸体接触力模型

采用郭嘉楠等描述的粗糙表面碰撞模型，有如下假设：①微凸体为半径相同的球体；②微凸体分布为各向同性且服从正态分布；③忽略微凸体塑性变形。碰撞接触力为

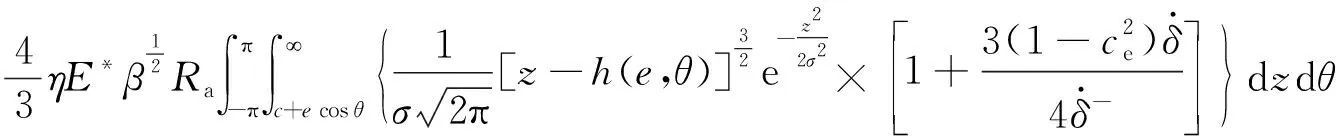
(6)

式中:E*为等效弹性模量；β为微凸体半径；Ra为碰撞体等效半径；η为微凸体分布密度；σ为微凸体分布均方根；z为微凸体高度分布；c为间隙大小；e为滑架体-刨头几何中心相对偏移量；δi为接触变形量。

2.2 刨头-煤粉层-滑架体接触力模型

建立刨头-煤粉层-滑架体接触面之间接触力模型，有如下假设：①假设煤粉层中的煤粉颗粒为各向同性且尺寸均匀的球体；②忽略煤粉颗粒塑性变形。等效之后接触模型如图5所示，在接触区域煤粉层承载为

(8)

(9)

式中:N为承载煤粉颗粒总数；d为煤粉颗粒直径；hi为煤粉颗粒有效承载区的高度；vp,Ep分别为煤粉颗粒泊松率和弹性模量；v为接触表面的泊松率；ρ为煤粉颗粒密度；λ为煤粉颗粒浓度；Q为煤粉颗粒流量；hx为介于最大与最小膜厚之间的厚度；h0为最小膜厚；h1为最大膜厚。

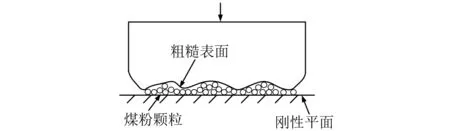
图5 三体等效接触示意图Fig.5 Three-body equivalent contact diagram

结合Lankarani Nikaravesh模型，刨头-煤粉层-滑架体接触力模型可表示为

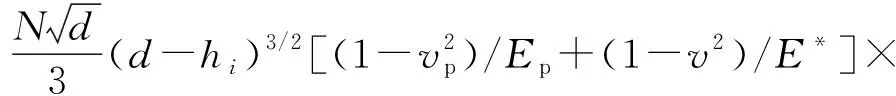
(10)

2.3 恢复系数的确定

为了获得刚性体-微凸体接触力模型以及刨头-煤粉层-滑架体接触力模型中的接触阻尼，关键是对碰撞恢复系数的测定。本文采用自行设计的试验装置，整体布局如图6所示，四周采用有机玻璃筒壁放置煤粉颗粒，当测量刚性体-微凸体碰撞恢复系数时可去掉，底部采用合金结构钢，通过三维表面形貌仪测得其表面粗糙度为6.3 μm，利用不锈钢球作为冲击重物，质量为0.5 kg，直径为5 cm，下落高度为H=100 mm，煤粉颗粒密度为2.5 g/cm3，颗粒粒径为150 μm。采用Photron fastcam Mini高速摄像系统拍摄碰撞全过程，拍摄分辨率设定为1 024×1 024，设置拍摄频率为6 400 fps(每秒钟拍摄6 400幅照片)。试验时，不锈钢球从一定高度上自由落体碰撞到煤粉/合金结构钢上(重复3次采集数据取均值)。采用运动学方程计算出碰撞前和碰撞后的速度，通过恢复系数的定义推导出恢复系数的大小[20-22]，如式(11)所示，本文仅列出了含煤粉层条件下的碰撞过程截图，如图7所示。

(11)

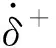
本文选取煤粉层厚度作为变量进行测试，测试计算结果如表1所示，由表1可知，未加入煤粉颗粒时，刚性体-微凸体接触碰撞恢复系数为0.85，相比加入煤粉颗粒时的数值大一些，这是由于加入了煤粉颗粒引起一定量的能量损失所致。

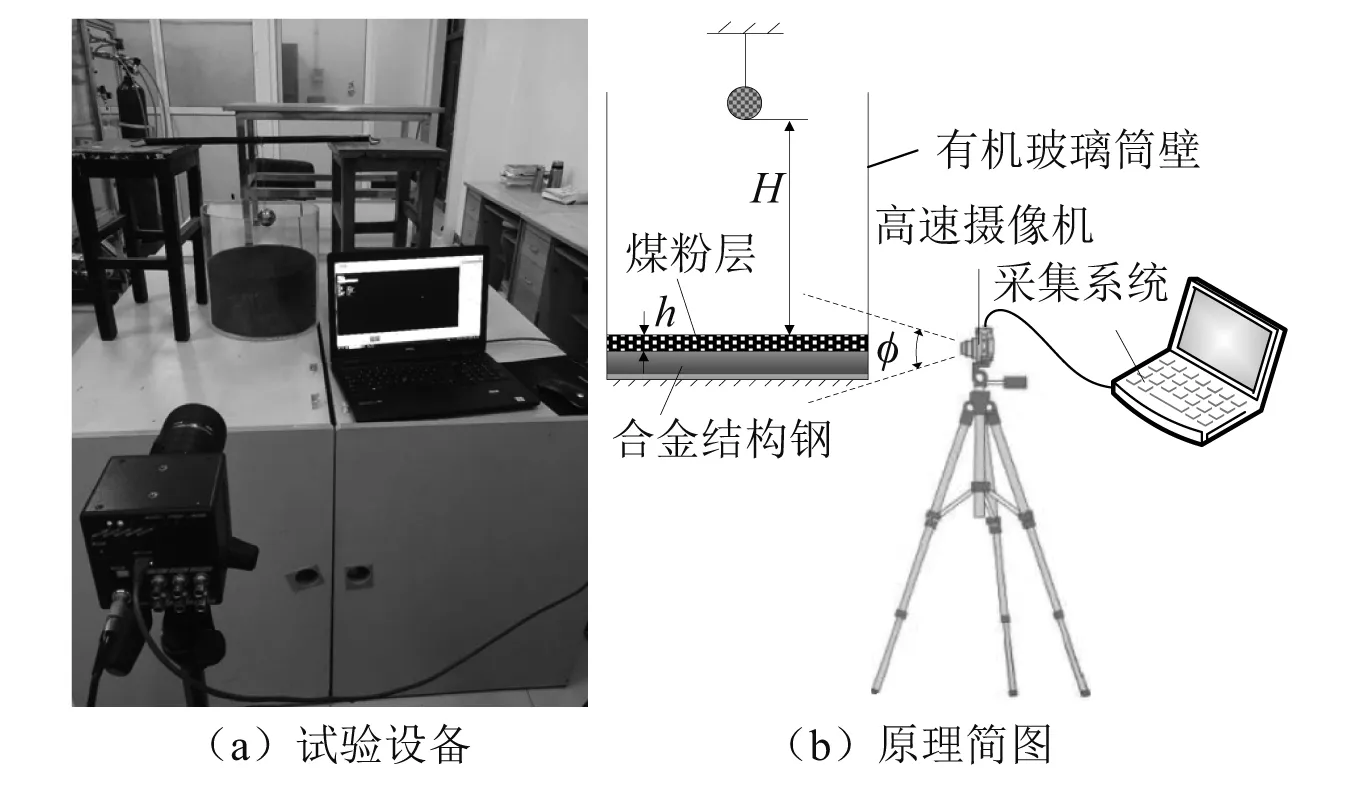
图6 试验设备布局Fig.6 The layout of the experimental device

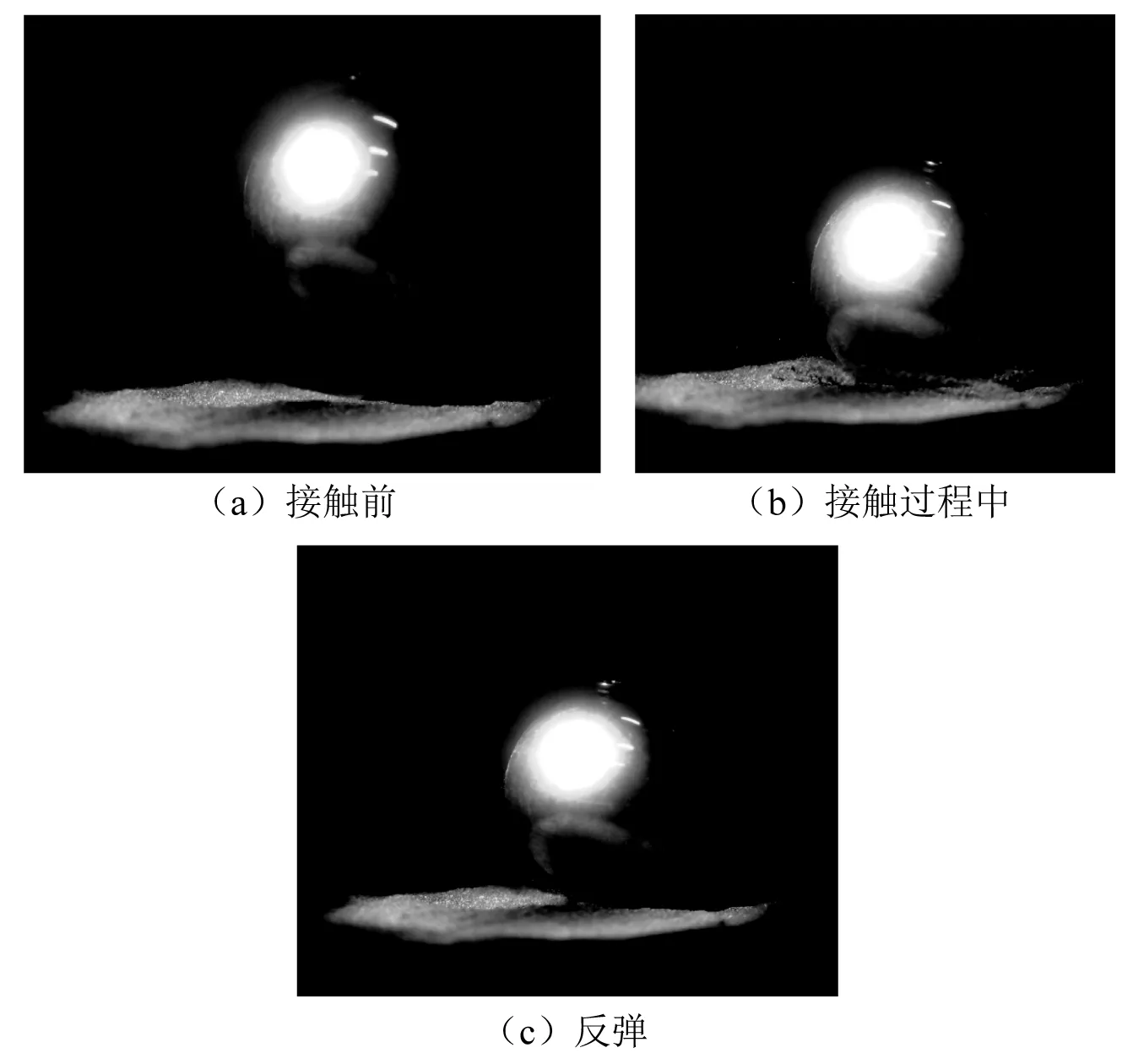
图7 碰撞过程Fig.7 Collision process

表1 恢复系数测量值Tab.1 Recovery coefficient measurements

3 三维动力学模型

利用牛顿运动定律分析刨头受力状态，将局部坐标系设定在滑架体中心，如图8所示，建立刨头-滑架体三维空间动力学模型，如式(12)所示

(12)

式中:x为竖直方向振动位移；y为垂直煤壁方向的振动位移；z为切向振动位移；α为绕X坐标轴旋转的角度；β为绕Y坐标轴旋转的角度；θ为绕Z坐标轴旋转的角度；FN为滑架体对刨头的支撑力，N；lg1,lg2分别为刨头重力对滑架体z′轴、y′轴的力臂，m；I为刨头转动惯量，kg·m2；m为刨头的质量，kg；G为刨头重力，N；Fx,Fy1,Fy2,Fy3,Fz为刨刀的侧向力、法向力；刨削阻力，N；Fa为刨头的拉力，N；Ff为刨头的摩擦力，N；ly1,ly2,ly3分别为刨头法向力对z轴的力臂，m；lx1,lx2分别为侧向力对x轴、y轴的力臂；lfy为摩擦力对y轴的力臂，m；Fτ为碰撞力引起的切向摩擦力，N，采用库仑摩擦力模型,Fτ=μFNi，μ为摩擦因数，FNi(i=1,2,3,4,5,6,7,8)为各点碰撞力，N,当1,2,6,7点产生碰撞时采用微凸体-颗粒接触力模型，当3,4,5,8点产生碰撞时采用微凸体接触力模型。

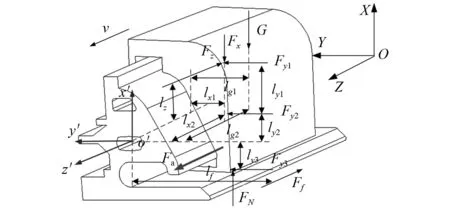
图8 刨头受力分析模型Fig.8 Mechanical model of the plow head

4 数值仿真

利用MATLAB数学软件进行数值计算分析，以BH38/2×400型刨煤机的结构参数为例，具体参数为：m=2 430 kg，I=1 265 kg·m2，lx1=0.72 m，lx2=0.415 m，lx3=0.01 m，ly=lyN=0.615 m，lg=0.255 m，ly1=0.21 m，ly2=0.2 m，ly3=0.22 m，lfy=0.3 m,Fx=10 kN,Fy1=90 kN,Fy2=30 kN,Fy3=95 kN,Fz=100 kN，仿真得到响应图如图9所示。

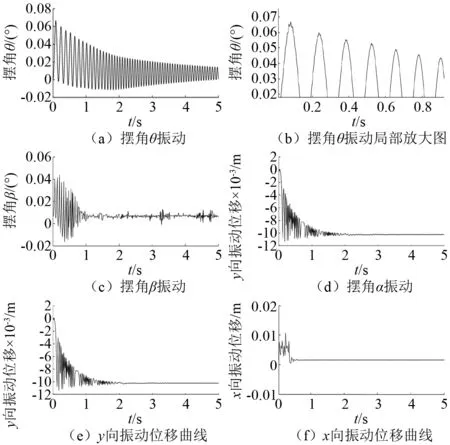
图9 碰撞振动响应图Fig.9 Collision vibration response

图9为刨头各向碰撞振动响应曲线，由图9可知，受刨头重力以及外部截割载荷影响，刨头各向振动仅在初始时刻产生一段时间的波动，随后振动逐渐减小；从波动幅度可知，摆角θ的振动相比其他方向的振动大一些，且波动衰减时间最长，x向振动位移波动幅度最大，波动衰减时间最短。此外，从如图9(b)可以看出，在刨头与滑架体间隙边界处产生碰撞振动，随着能量的损失，碰撞振动逐渐减小。

图10和图11为截面1、截面2内刨头与滑架体各关键点的碰撞力，由图可知，各点的碰撞力幅值在初始时刻产生了一定的衰减，随后1点～6点碰撞力趋于恒值，说明刨头与滑架体在此点一直处于接触，即此时产生了多面接触，7点、D8点碰撞力趋于0，说明此时一直处于分离状态。从各点的碰撞力幅值可以看出，1点、2点的碰撞力大一些，3点～6点小一些，7点的碰撞力最小。图12为截面1、截面2的局部放大图，由图可知，在0.217 s时刻截面2中4点、5点同时产生了接触碰撞，此时刨头与滑架体产生了线碰撞。在0.23 s时刻截面1中4点、5点和截面2中5点同时产生了接触碰撞，说明此时刨头与滑架体产生了面碰撞。在0.275 s时刻，截面1中4点产生了单点碰撞。

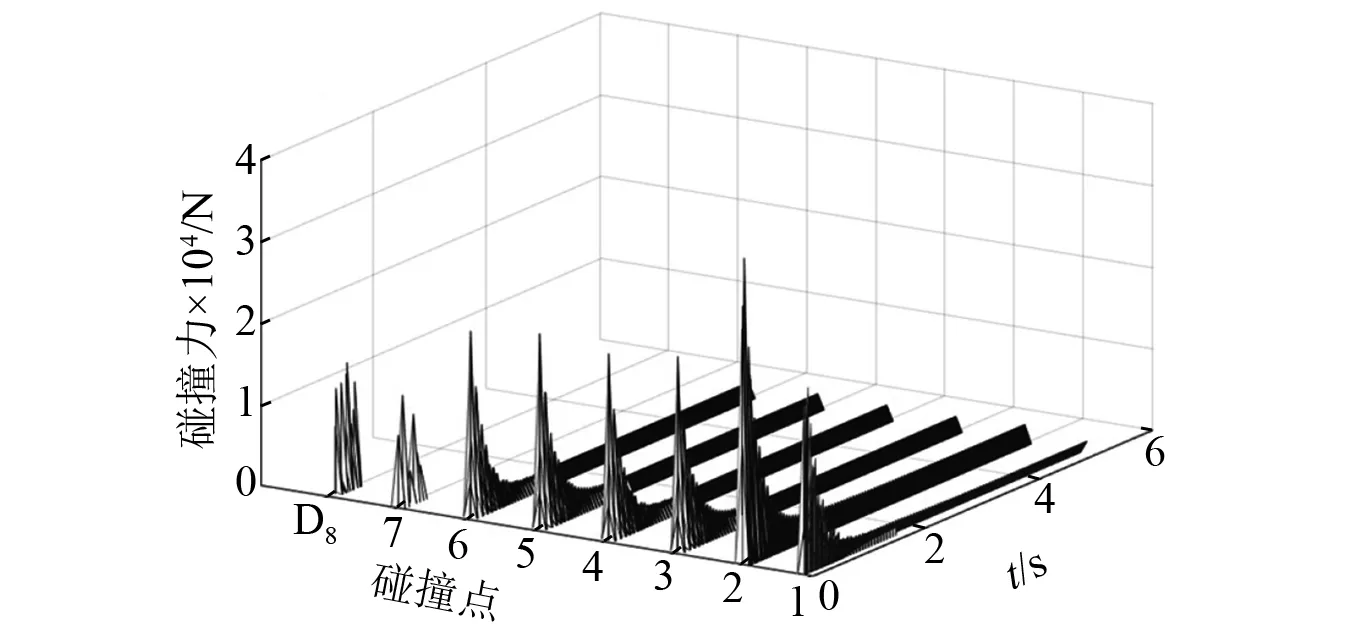
图10 截面1中各点碰撞力Fig.10 The collision force of each point in section 1

图11 截面2中各点碰撞力Fig.11 The collision force of each point in section 2

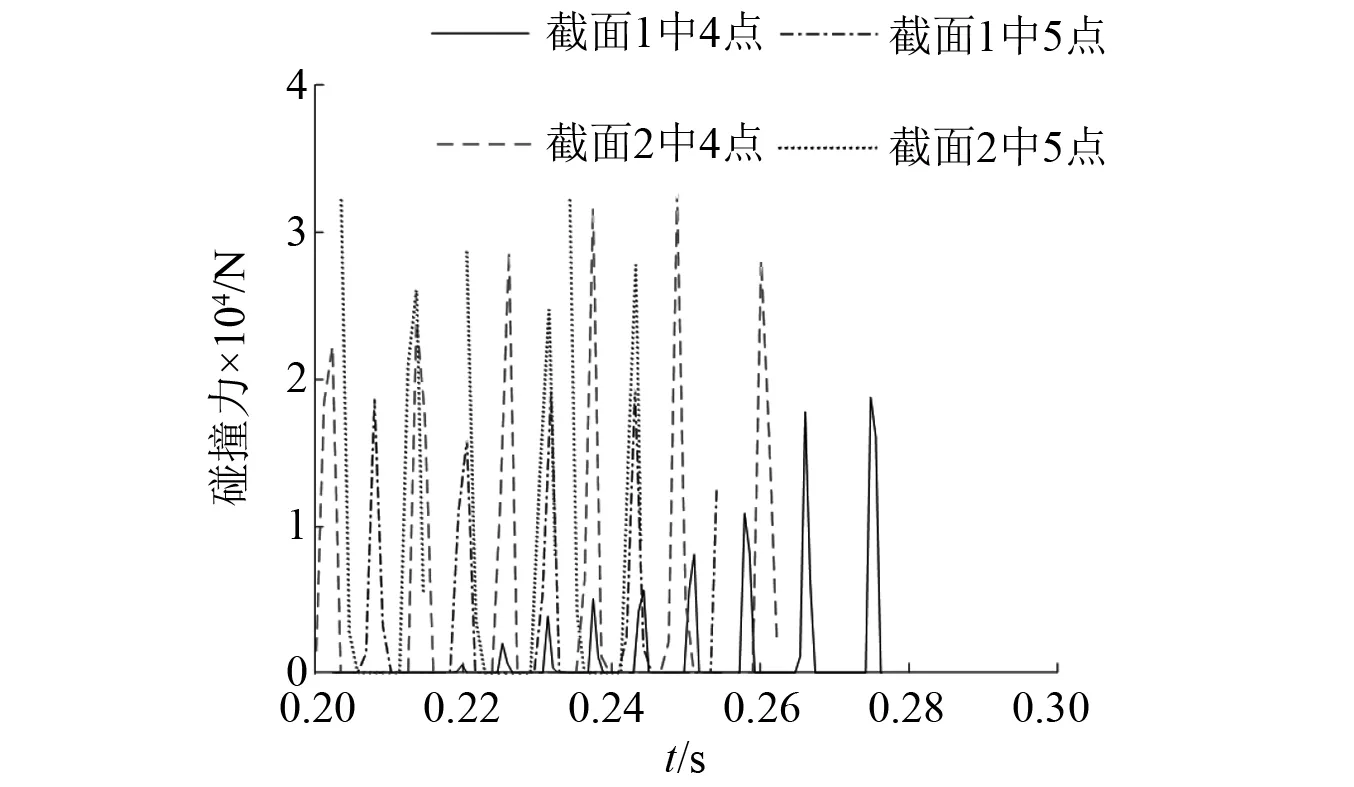
图12 局部放大图Fig.12 Local magnification

4.1 恢复系数对刨头碰撞振动的影响

为了研究恢复系数对刨头碰撞振动的影响，以刨头绕x轴的摆角振动、y向振动位移响应为例进行分析，图13展示了刨头绕x轴的摆角振动、图14展示了刨头沿y向振动位移，图15为绕x轴的摆角振动的局部放大图，通过分析可知，随着恢复系数的降低，引起的碰撞能量损失增大，使刨头绕x轴的摆角振动、y向振动位移幅值降低，刨头与滑架体在间隙边界处的接触碰撞振动幅值也随之降低，且随着恢复系数的降低，摆角振动持续时间随之缩短。图16为恢复系数对刨头与滑架体关键点的碰撞力均值影响分布图，图17为恢复系数对刨头与滑架体关键点的碰撞次数影响分布图，通过分析可知，随着恢复系数的降低，刨头与滑架体各点的碰撞力均值有所降低，碰撞次数也随之降低，但对1点、D8点碰撞次数影响不明显。

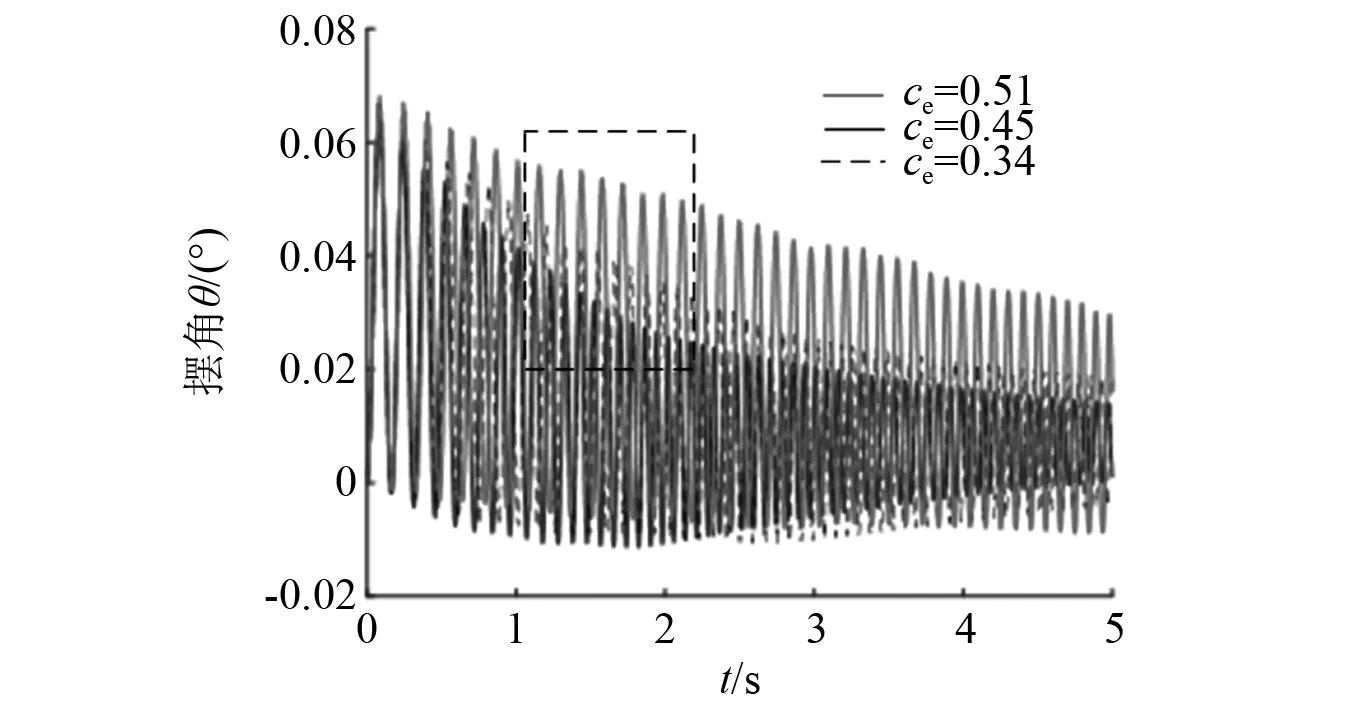
图13 恢复系数对摆角θ振动的影响Fig.13 The effect of restitution coefficient on the swing angle θ vibration

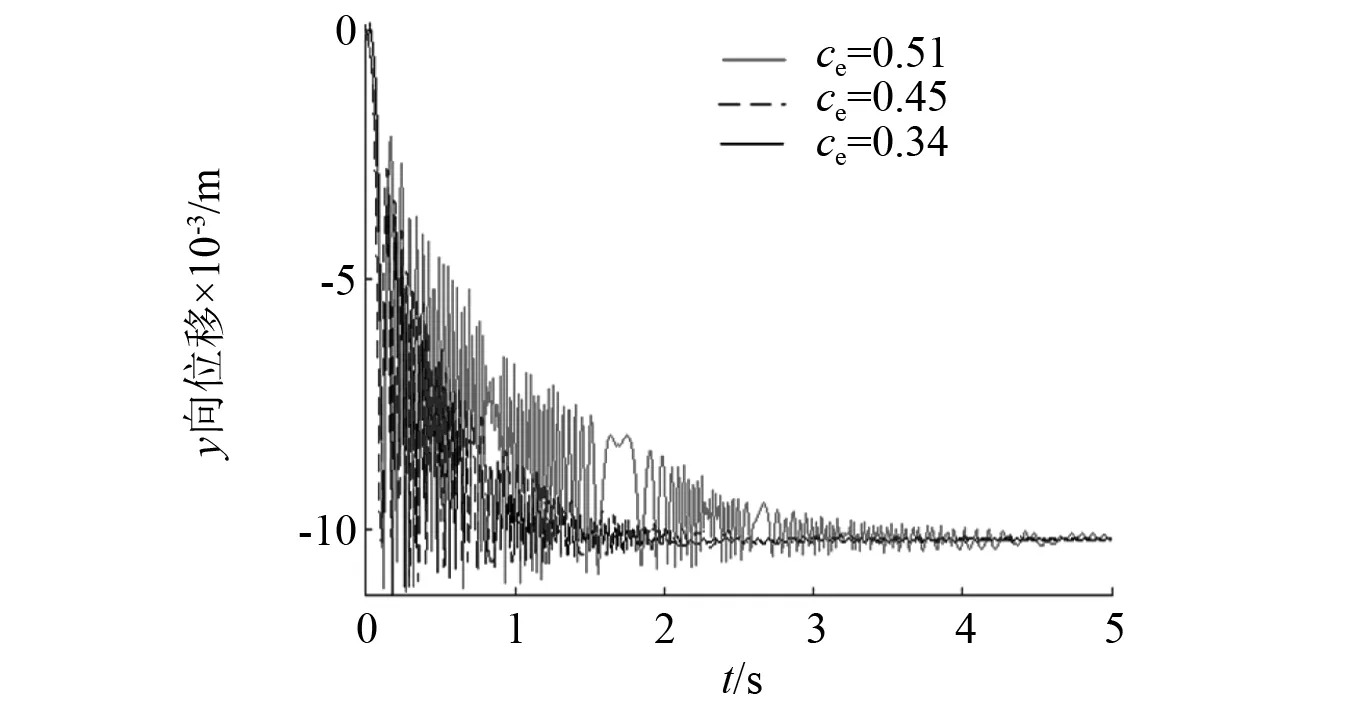
图14 恢复系数对y向振动位移的影响Fig.14 The effect of restitution coefficient on the vibration displacement in the y direction

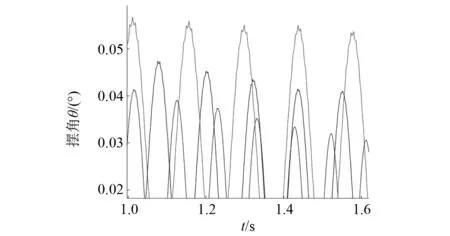
图15 摆角θ振动的局部放大图Fig.15 Local magnification of the swing angle θ vibration

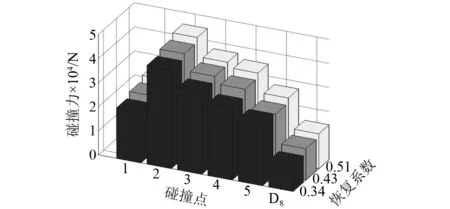
图16 恢复系数对碰撞力均值的影响Fig.16 The effect of restitution coefficient on the mean of collision force

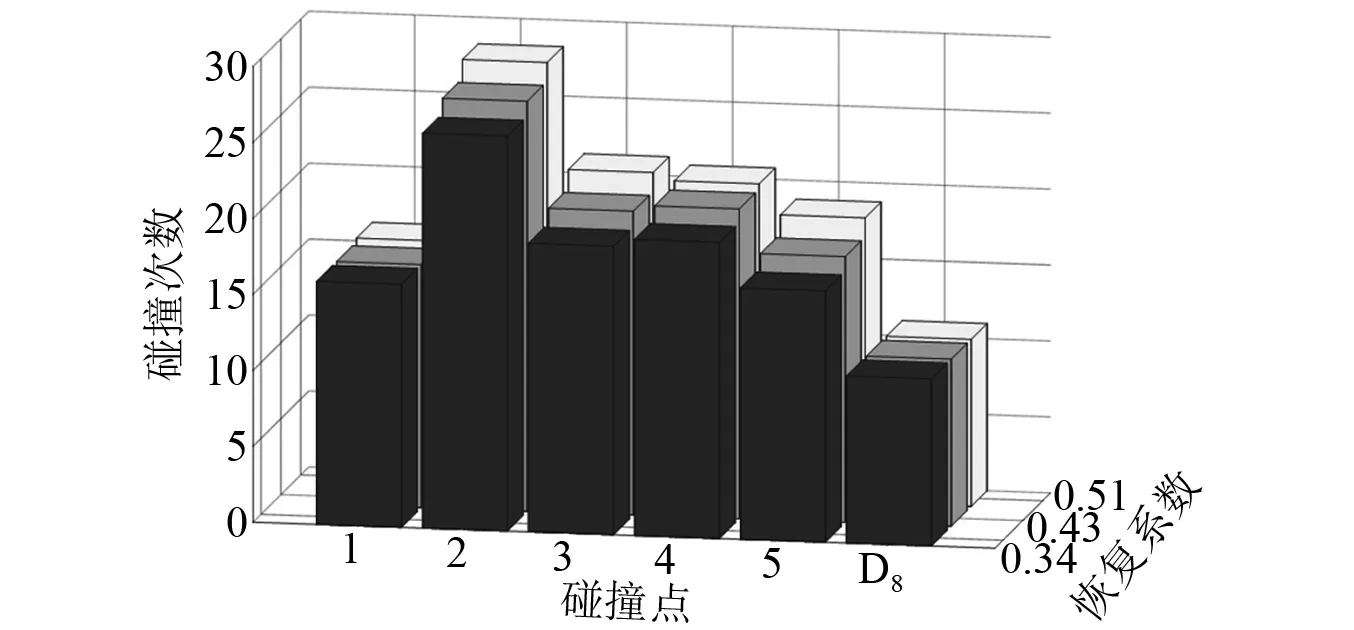
图17 恢复系数对碰撞次数的影响Fig.17 The effect of the restitution coefficient on the number of collisions

4.2 水平间隙对刨头碰撞振动的影响

为了研究水平间隙对刨头碰撞振动的影响，以刨头沿y向振动位移为例进行分析，选取水平间隙分别为4 mm，5 mm，6 mm，图18展示了刨头沿y向振动位移，通过分析可知，随着水平间隙的增大，刨头与滑架体在间隙边界处的接触碰撞振动幅值随之增大。图19为水平间隙对刨头与滑架体关键点的碰撞力均值影响分布图，图20为水平间隙对刨头与滑架体关键点的碰撞次数影响分布图，通过分析可知，随着水平间隙的增大，刨头与滑架体各点的碰撞力均值有所升高，碰撞次数也随之增多。

图18 水平间隙对y向振动位移的影响Fig.18 The effect of horizontal clearance on the vibration displacement in the y direction

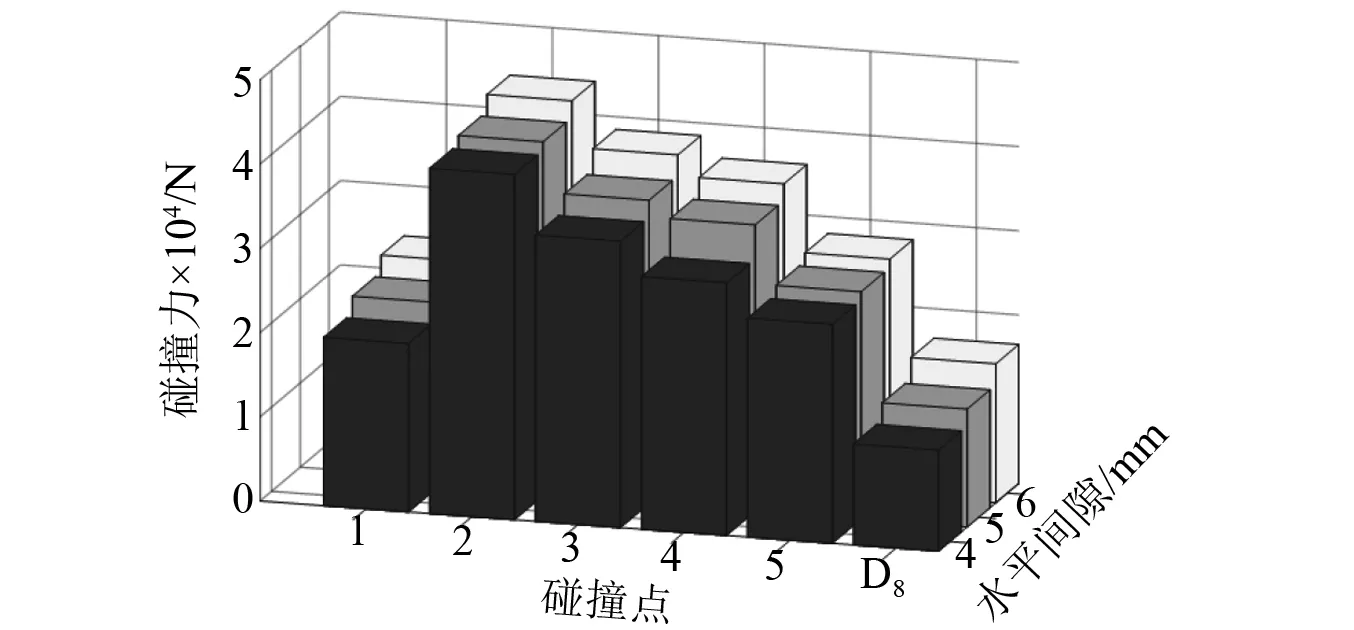
图19 水平间隙对碰撞力均值的影响Fig.19 The effect of horizontal clearance on the mean of collision force

图20 水平间隙对碰撞次数的影响Fig.20 The effect of horizontal clearance on the number of collisions

4.3 刨削速度对刨头碰撞振动的影响

为了研究刨削速度对刨头碰撞振动的影响，同样以刨头沿y向振动位移为例进行分析，选取刨削速度分别为0.5 m/s，0.7 m/s，1.0 m/s，图21展示了刨头沿y向振动位移，通过分析可知，随着刨削速度的增大，刨头与滑架体在间隙边界处的接触碰撞振动幅值随之增大。图22为刨削速度对刨头与滑架体关键点的碰撞力均值影响分布图，图23为刨削速度对刨头与滑架体关键点的碰撞次数影响分布图，通过分析可知，随着刨削速度的增大，刨头与滑架体各点的碰撞力均值增大，碰撞次数也随之增多，但增加幅度不大。

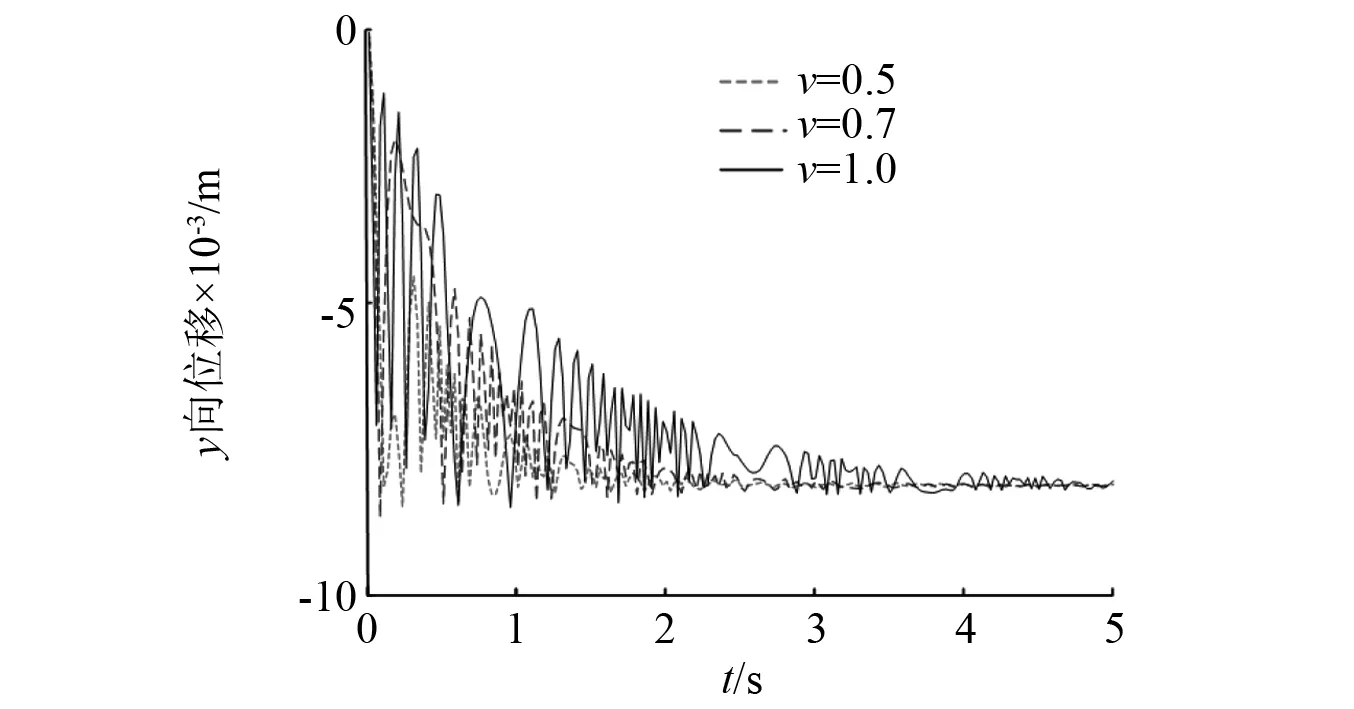
图21 刨削速度对y向振动位移的影响Fig.21 The effect of plow speed on the vibration displacement in the y direction

5 试验验证

为了验证本文方法及所建模型的正确性，基于中煤张家口煤矿机械有限公司的国家能源采掘装备研发实验中心综采工作面力学检测分析试验平台，对刨头振动进行检测试验，测试系统如图24所示，测试传感器采用压阻式加速度传感器，受空间的限制，将传感器安装在顶刨刀座左端，测试刨头垂直煤壁方向的振动量，通过DH5920N振动测试系统中无线采集模块进行实时数据采集，数据通过无线网络传送到计算机进行存储。

图22 刨削速度对碰撞力均值的影响Fig.22 The effect of plow speed on the mean of collision force

图23 刨削速度对碰撞次数的影响Fig.23 The effect of plow speed on the number of collisions

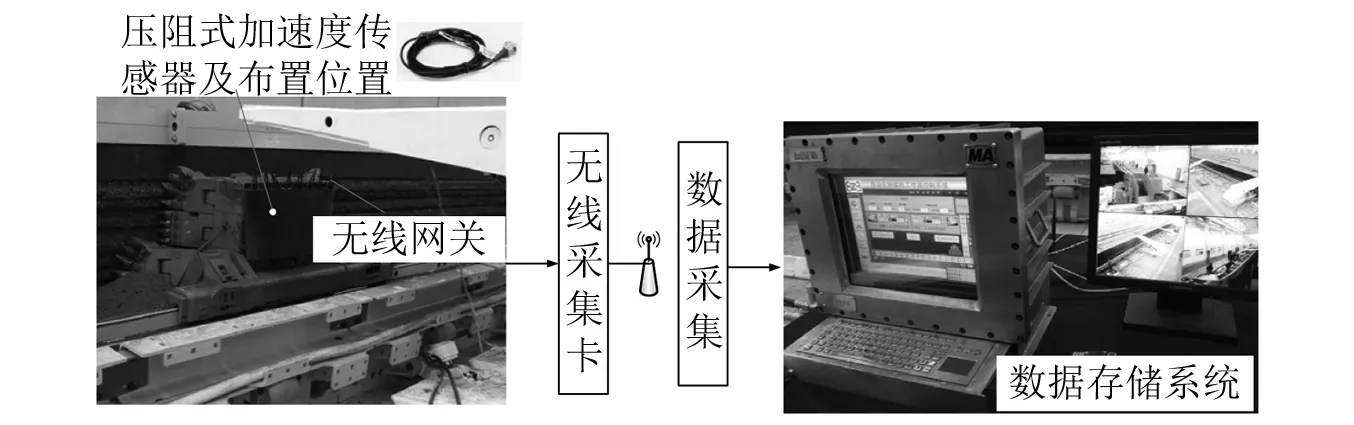
图24 刨头振动测试系统Fig.24 Vibration test system on the plow head

本试验中振动传感器安装位置与刨头理论中心坐标点选取存在一定距离，直接进行结果对比将会存在较大的误差，因此需要对试验测试结果进行转化，如图25所示为传感器布置位置与理论中心坐标位置关系。

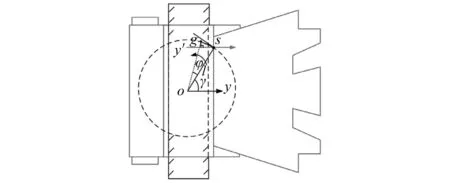
图25 位置关系转换Fig.25 Transformation of positional relationship

令y′为测试传感器的测得结果，s点为测试传感器布置位置，s点随着刨头的振动将同时产生摆动和沿y的水平振动，当s以角度φ摆动到g点时将在y向产生附加位移，因此，测试结果为的位移结果y′与y附加位移结果之和，即

y′=y-lφsinγ

(13)

式中:γ为测试传感器位置与x向的夹角；l为理论中心坐标点与传感器布置位置的距离；φ为刨头振动角度，由于刨头振动角度较小，则sinφ≈φ。

为了降低数值求解结果与实测结果的误差，刨头中刨刀所受载荷激励采用试验测试结果，选取刨速为1 m/s，刨深分别为5 mm，10 mm，15 mm工况测试结果作为外载输入，图26仅列举了速度为1 m/s，深度为5 mm，单把刨刀的三向力测试结果。

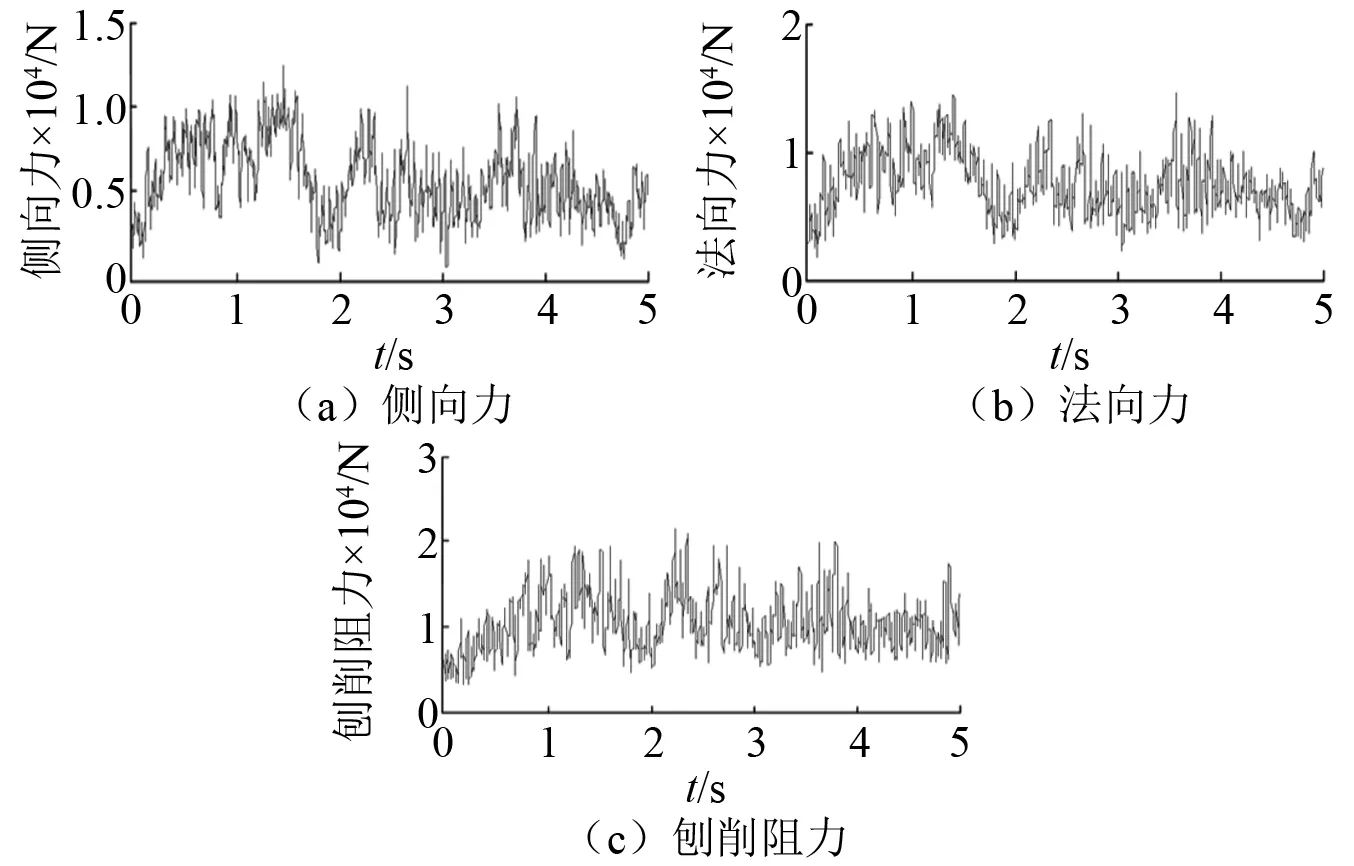
图26 刨刀三向力测试结果Fig.26 Results of triaxial forces on a single plow bit

图27～图29为刨头加速度测试曲线及本文仿真结果曲线对比结果。通过分析可知，在三种不同刨深条件下，采用本文方法求解得到的刨头振动加速度曲线与试验测得的曲线波动规律基本一致。图30对不同刨深工况下的试验及仿真结果进行了局部放大对比，由图可知，刨头在运动过程中与滑架体在边界处产生了多次碰撞，试验碰撞规律与仿真求解的碰撞规律基本一致。对图27～图29进行数据统计，表2列出刨头振动加速度的试验平均值与数值求解平均值以及采用文献[23]模型求解的结果。由表2可知，采用本文方法求解的结果与试验测试结果的变化规律相符，且数值误差均在10%以内，而文献[23]模型求解结果与试验测试结果误差相差较大，验证了本文方法的有效性及准确性。文献[23]模型产生误差的原因：①模型尺寸与实际结构尺寸相差大；②模型未考虑三维间隙碰撞的耦合作用；③接触模型中未考虑微凸体以及煤粉颗粒的影响。本文模型虽然对结构模型以及接触力学模型均有所改进，但仍存在一定的误差，产生误差的原因主要有：①数值求解过程存在截断误差；②理论分析中，采用刨煤机的设计尺寸进行分析，未考虑刨煤机整机在装配过程中装配误差对设计尺寸的影响；③理论分析中，未考虑刨煤机整机振动对刨头-滑架体振动的影响。

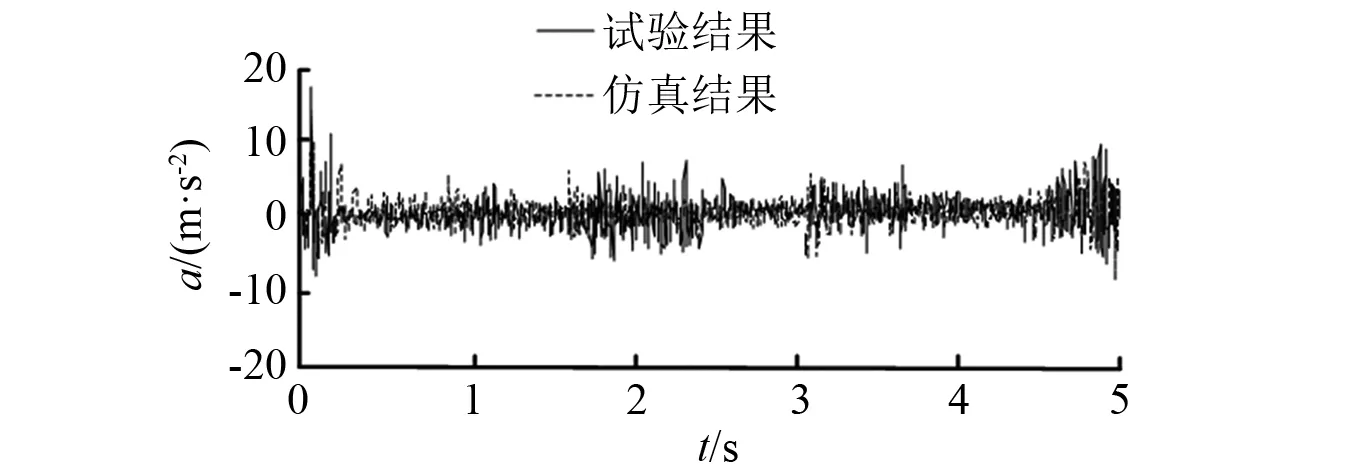
图27 刨深为5 mm时试验与仿真结果对比Fig.27 Comparison of the experimental results and the simulation results with a planing depth of 5 mm

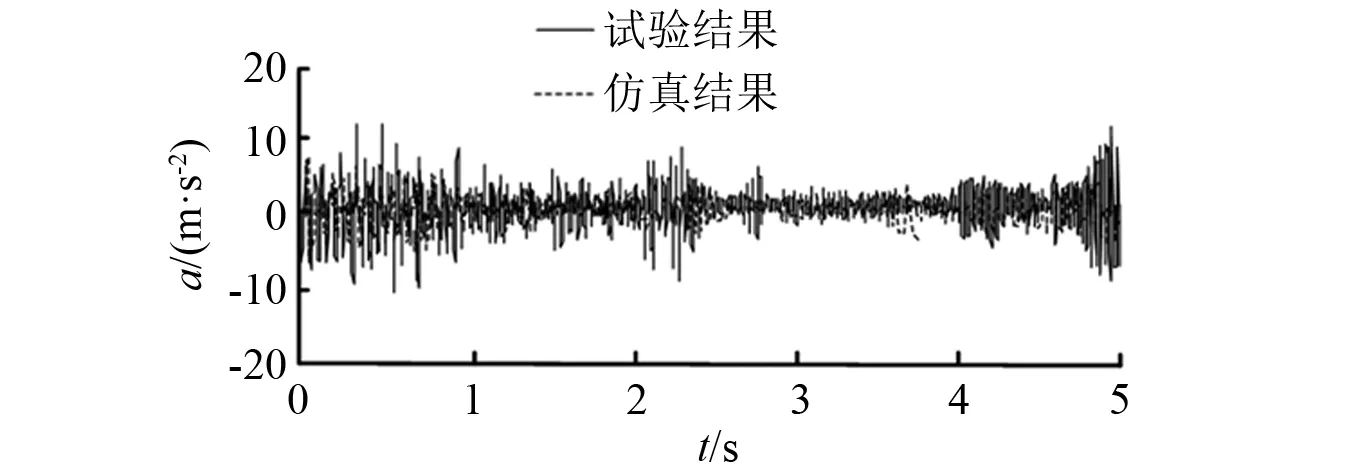
图28 刨深为10 mm时试验与仿真结果对比Fig.28 Comparison of the experimental results and the simulation results with a planing depth of 10 mm

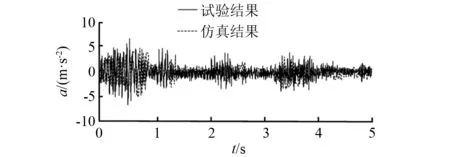
图29 刨深为15 mm时试验与仿真结果对比Fig.29 Comparison of the experimental results and the simulation results with a planing depth of 15 mm

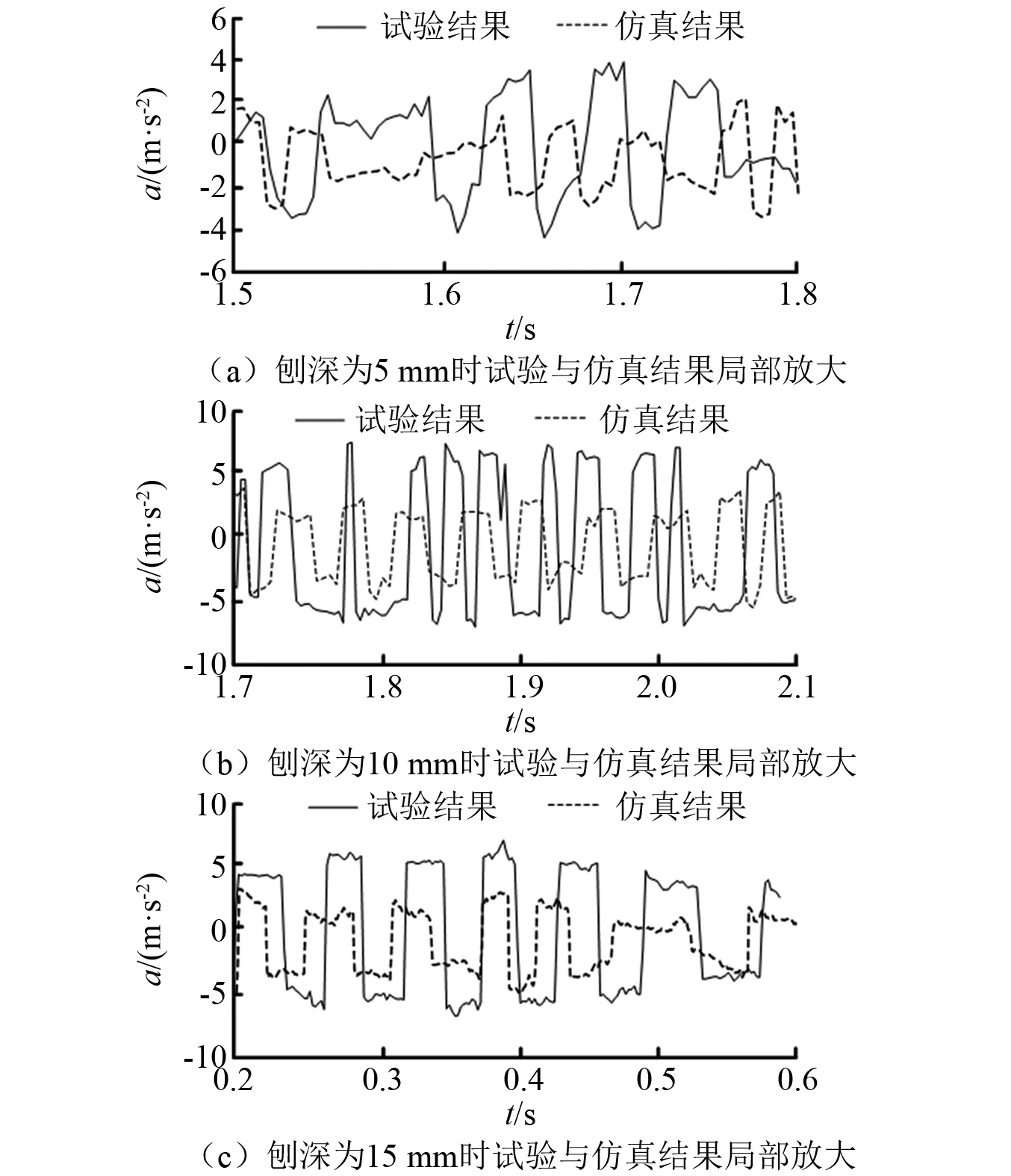
图30 试验与仿真结果局部放大图Fig.30 Local amplification of experimental and simulation results

表2 理论与试验对比Tab.2 Comparison of theoretical and experimental results

6 结 论

针对刨头-滑架体三维结构特点，提出了将三维多面体碰撞检测降维到二维多边形碰撞检测方法，综合考虑接触表面粗糙度、接触表面煤粉颗粒的界面作用，构建了刨头与滑架体间三维接触碰撞动力学模型，通过数值求解得到如下结论：

(1)受重力及外载荷的影响，刨头各向的振动仅在初始时刻产生一段时间的波动，随着时间的推移波动逐渐衰减，最终趋于平稳，且在刨头与滑架体间隙边界处的碰撞振动随着能量的损失逐渐减小；此外，由于刨头-滑架体三维几何结构的特征，在外力作用下，刨头-滑架体的接触碰撞存在点、线、单面、多面等多种形式。

(2)随着恢复系数的降低，刨头绕x轴的摆角振动、y向振动位移的幅值随之降低，刨头与滑架体在间隙边界处的接触碰撞振动幅值也随之减小，且摆角振动持续时间随之缩短。此外，随着恢复系数的降低，刨头与滑架体各点的碰撞力均值有所降低，碰撞次数也随之降低。

最后，通过将本文模型求解结果与试验测试结果对比得到二者变化规律基本一致，且数值误差在10%以内，可见所构建的动力学模型具有一定的有效性及准确性。