一种惯质黏滞阻尼器的性能及其对拉索减振效果的试验研究

刘 菁， 梁 栋,2

(1. 河北工业大学 土木与交通学院，天津 300401；2. 河北省土木工程技术研究中心，天津 300401)

拉索作为斜拉桥重要的受力构件，具有柔度大、单位长度质量较轻且固有阻尼小的特点，很容易产生涡激共振、参数共振、尾流驰振、抖振和风雨激振[1-7]。因此，拉索振动控制成为斜拉桥结构的重要问题[8-9]，其中附加外置黏滞阻尼器可以直接增加拉索的模态阻尼，是拉索减振措施中最为常用的方法[10-11]。但附加外置黏滞阻尼器仅能使拉索某一阶模态获得最优模态阻尼比，且安装位置一般不超过索长的5%[12-13]，这极大的限制了黏滞阻尼器的减振效果。

藉此，可行的策略是提高近锚固端阻尼器的减振耗能性能，近来已引起了研究者们相当大的关注。具有负刚度元件的阻尼器可以相对增大阻尼器的变形幅度[14-15]，从而增加振动中的能量消耗，并实现更大的阻尼比。随着力学放大机制(如滚珠丝杠、齿轮齿条、杠杆摆，以及利用流体惯性的惯性泵等)的利用，惯质器可以提供较大的表观质量，相应的惯性力所体现的负刚度效应也逐渐用于结构振动控制。自2015年，研究者开始尝试将惯质器用于斜拉索减振。Lazar 等[16-17]将调谐质量阻尼器中的质量部分替换成惯质器，得到了调谐惯质阻尼器(tuned inerter-mass damper,TID)。针对拉索第一阶振动模态的减振分析表明，当安装高度相同时，TID可使拉索获得比传统黏滞阻尼器更高的模态阻尼比。Chen等[18-19]将被动负刚度装置应用于拉索附加阻尼器系统，以克服由于阻尼器安装位置限制而引起的附加阻尼不足的问题，并讨论了由于负刚度引起的控制力的非线性对系统分析的影响。Luo等[20]利用有限元方法研究了3种惯质器应用于张紧索的临界阻尼比，分析表明将惯质器应用于拉索减振可获得较好的减振效果。Shi等[21-23]提出了由提供负刚度的磁铁和油阻尼器合成的负刚度阻尼器，数值分析和试验验证了该阻尼器对拉索第一阶振型的减振性能远优于传统黏滞阻尼器。Lu等[24]采用数值方法分析了黏滞惯性质量阻尼器对张紧拉索的减振效果。其中，拉索第一阶模态的最大阻尼比达到了传统黏滞阻尼器的9倍；甚至当安装位置降低至2%索长时，依然表现出了良好的减振效果。莫凯程[25]对利用滚珠丝杠惯性质量阻尼器抑制拉索振动进行了数值仿真和试验验证，结果表明：最优参数不同的惯性质量阻尼器可以大幅提高斜拉索指定阶次的模态阻尼比。崔智鑫[26]用数值方法讨论了三种构型的调谐惯质类阻尼器对拉索第一阶振动的减振性能，指出并联惯质装置优于串联。Chen等[27]研究了理想的NSD模型和典型IVA模型，指出NSD可以平均各阶拉索振动的阻尼。同时，为了平衡拉索各阶模态的阻尼效果，在使用IVA模型时存在阻尼增强的上限。

目前，利用惯性质量对拉索进行减振的研究还处于起步阶段，大多只开展了理论研究。至于如何在实际拉索减振中实现惯质减振，则还需要开展更加多样化的惯质系统研究。为方便地实现惯质，本文设计并制作了包括齿轮齿条、惯质元件和黏滞阻尼元件在内的拉索用惯质阻尼器，开展了相应的理论分析、阻尼器自身性能试验及其与模型索的组合试验。

1 拉索-惯质黏滞阻尼器减振的理论分析

1.1 垂度拉索的平面内振动

考虑拉索为均质拉索，且按照角度α倾斜，如图1所示。本文研究了具有垂度的拉索[28]，当垂跨比小于1/8时，设拉索弦向索力为H，由振动引起的索力变化为ΔH，拉索单位长度质量为ρ，拉索的弹性刚度为EA，索的总长为L，阻尼器的位置在距离拉索桥面锚固端xd位置。

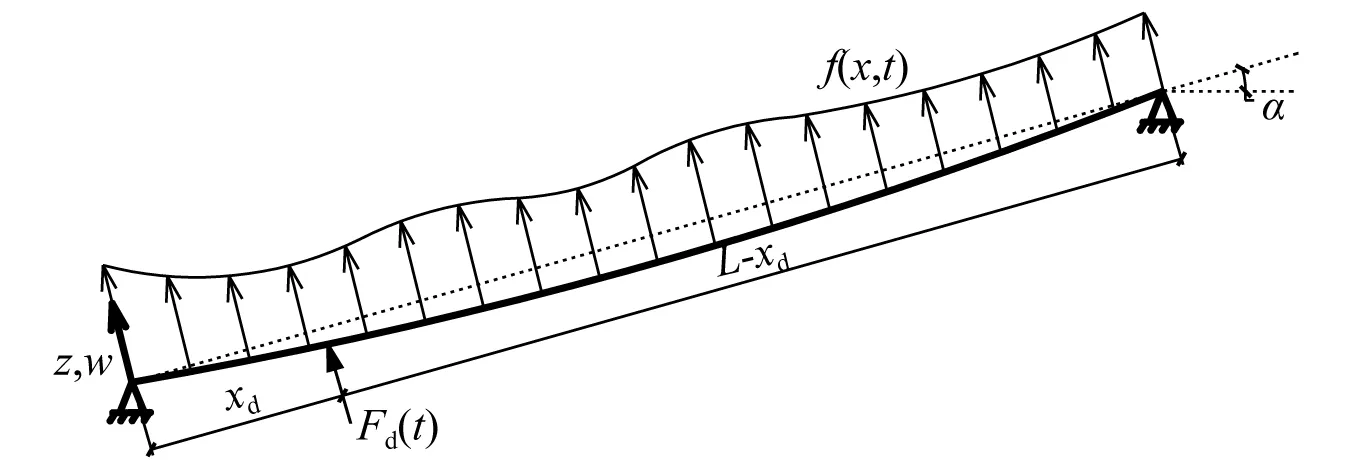
图1 倾斜垂索的平面静态构型Fig.1 In-plane static profile of inclined shallow cable

由Krenk等[29]研究可知，垂度拉索的运动方程为

(1)

式中：z(x)=4d(1-x/L)x/L为拉索静态构型方程；d=ρgL2cosα/8H为拉索跨中垂度；δ(x-xd)为克罗内克delta函数； 拉索附加张力的表达式为

(2)

式中：Le≈L[1+(ρgLcosα/H)2/8]为拉索静态延展长度；并考虑如下无量纲量

(3)

式中：无上标的为有量纲的变量；上标为横线的为无量纲变量。将式(2)与式(3)代入式(1)中，并化简可得拉索平面内振动无量纲方程为

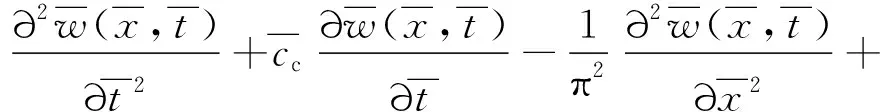
(4)

式中，λ2为Irvine参数

(5)

1.2 拉索-惯质黏滞阻尼器体系的改进Galerkin方法求解

早期研究者采用包含350个自由度的正弦形状函数叠加的Galerkin方法[30]，来模拟拉索的面内振动。即使采用混合型有限元方法[31]也需要大量自由度以确保分析结果的精确性。于是，Johnson等[32]提出了“控制导向”的改进Galerkin模型，该模型包含正弦形函数与静态挠曲形函数两部分，能够极大的提高数值模型的计算效率。改进Galerkin方法通过有限级数之和来近似拉索的平面内振动，有如下方程

(6)

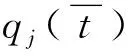
(7)

将式(6)和式(7)代入式(4)中，可得到含有质量矩阵M、阻尼矩阵C，与刚度矩阵K的无量纲方程。

(8)

质量矩阵M、阻尼矩阵C，与刚度矩阵K详细的推导过程可参考文献[33]中的式(15)～式(17)。

(9)

阻尼器阻力的位置向量φ表示为

(10)

由上述分析可知，通过改进Galerkin方法对模态振型的假设与逼近，能够使振动方程无量纲化以便分析，但仍然无法使振动式(8)解耦。

1.3 拉索-惯质黏滞阻尼器减振体系的状态空间方程

为求解式(8)，现其改为状态空间方程的形式，如式(11)

(11)

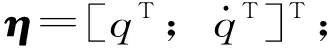
(12)

同时，将如式(13)所示的黏滞阻尼力矩阵，推广到惯质阻尼器的阻尼力矩阵，如式(14)

(13)

(14)

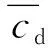
2 惯质黏滞阻尼器

本文制作的惯质黏滞阻尼器如图2所示。在斜拉索发生振动时，齿条将斜拉索索夹处的直线运动传递至齿轮，引起齿轮、转轴及阻尼圆盘的转动，各部件圆周运动产生较大的惯性质量，能够产生明显的负刚度效应。后端的阻尼圆盘在阻尼液体中旋转产生阻尼力。这些力经齿轮放大后再通过齿条传递到斜拉索，从而抑制斜拉索的振动。

图2 拉索-阻尼器体系装配简图Fig.2 Assembly diagram of the cable-damper system

(15)

(16)

式中：l为齿轮的分度圆；w为拉索带动齿条上下运动的位移；F为惯质黏滞阻尼器运动端的力的大小。

T=Ti+Tc

(17)

式中：Ti为惯性扭矩；Tc为黏滞扭矩。

2.1 阻尼液及相应阻尼系数的确定方法

本文采用黏度较大的锂基润滑脂和黏度较小的液压油组成黏滞阻尼液，阻尼扭矩Tc可表示为[35]

(18)

式中： 剪切力τ=ηγ，γ为剪切应变率，η为阻尼液黏度；h为阻尼圆盘距离油箱壁的距离。则由阻尼液黏滞特性产生的阻尼力公式可表示为

(19)

2.2 惯质的组成及其数值

惯质黏滞阻尼器中的转动、平动的部分，在运动过程中都会产生惯质。式(19)中惯性扭矩Ti可表示为

(20)

将式(20)扭矩折算成阻尼器出力并考虑齿条所产生的惯性力，则阻尼器惯质产生的阻尼力可表示为

通过对在校生和实习生的统计得出如下结果。从表2中可以看出，在校生的各个维度和总得分情况要偏高于实习生，尤其是把握感和一致感两个维度，也就是说学生对于工作的认识情况和适应情况比在校时是呈下降表现的。

(21)

式中：I1，J1，M1分别为齿轮的转动惯量、回转半径和质量；I2，J2，M2分别为转轴的转动惯量、回转半径和质量；I3，J3，M3分别为阻尼圆盘的转动惯量、回转半径和质量；M4为齿条的质量。借此，可以确定其相应的放大系数n1～n4，具体如表1所示。

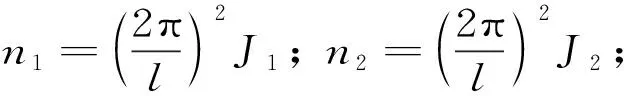
(22)

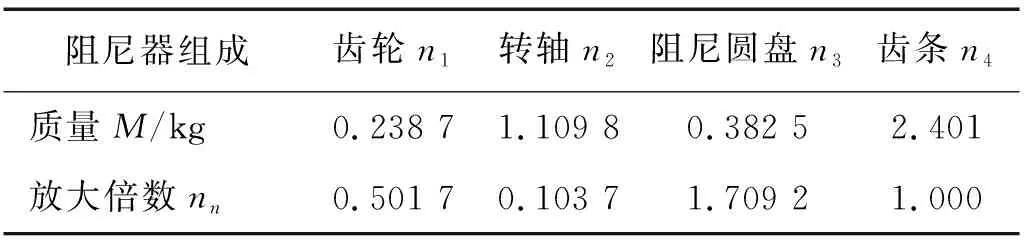
表1 阻尼器各组成部分的质量及放大系数Tab.1 Component’s mass and amplification factor

2.3 阻尼力计算公式

F=Fc+Fi

(23)

(24)

(25)

同时，在试验中应考虑轴承滚动摩擦导致的阻尼项和随动阻尼油导致的负刚度项的修正，应由下述试验得出。

3 拉索-惯质黏滞阻尼器的试验装置

根据试验条件和实验室具体情况，选用一根直径为9.3 mm的钢丝绳作为模型索，水平锚固在反力架上，采用安装质量块的方式增加缩尺拉索的自质量。模型索-阻尼器试验系统如图3所示，拉索各项参数，如表2所示。针对本次试验，惯质黏滞阻尼器安装在距离锚点L/6处，齿条端部安装一个量程为2.5 kN的拉压力传感器测量阻尼力时程；用量程为50 kN的压力传感器测量模型索索力；用量程为±150 mm的激光位移计测量模型索在在L/20，L/10，L/6和L/4处的位移时程，及拉索阻尼器远端L/10，L/6对称点处的位移时程。

图3 模型索-阻尼器试验Fig.3 Scale cable-damper test

图4 试验模型传感器布置图Fig.4 Sensors’ location of the test mode

表2 模型索的参数Tab.2 Parameters of the scaled cable

4 试验结果及分析

4.1 惯质黏滞阻尼器的负刚度

本文通过阻尼器不含阻尼液及阻尼圆盘的滞回曲线，来分析阻尼器的齿轮、齿条、转轴所产生的负刚度。在阻尼器无油且安装位置为L/6时，一阶振动试验力-位移曲线与理论计算力-位移曲线分别如图5(a)和图5(b)所示，一阶振动试验力-速度曲线与理论计算力-速度曲线分别如图5(c)和图5(d)所示。二阶振动试验力-位移曲线与理论计算力-位移曲线分别如图6(a)和图6(b)所示，二阶振动试验力-速度曲线与理论计算力-位移曲线分别如图6(c)和图6(d)所示。

图5 一阶振动试验与理论曲线Fig.5 First mode vibration test and theoretical calculation curve

图6 二阶振动试验与理论曲线Fig.6 Second mode vibration test and theoretical curve

由图5(a)和图6(a)中的力-位移曲线可知，在阻尼器无油且无阻尼圆盘时，齿条、齿轮、和转轴也产生了一定的负刚度和阻尼特性。因此，齿条、齿轮和转轴的负刚度不应在试验中忽略掉，其负刚度的数值由上述式(25)中的第1、第2和第4项计算，如图5(b)和图6(b)中的负刚度线所示。对阻尼器齿条端部的位移数据进行微分得出阻尼器齿条端的速度，绘制阻尼力-速度曲线图5(c)和图6(c)。试验力-速度曲线图5(c)和图6(c)与理论计算力-速度曲线图5(d)和图6(d)吻合较好，理论计算的力-速度曲线为椭圆曲线，由惯质元件与阻尼元件出力叠加所得。而阻尼元件(此时仅为轴承阻力)所得的阻尼力在力-速度曲线图5(d)和图6(d)中为一条斜线，说明在测试的频率与振动幅值下，本文设计的惯质黏滞阻尼器的轴承阻力是线性的。究其原因，是由于阻尼器的轴承在加工阶段的精度较高，轴承阻力不属于库伦摩擦阻力，而是由轴承滚动摩擦所产生的阻尼力，与轴承的等效阻尼系数与拉索振动速度的乘积有关，其特性与黏滞阻尼类似。故此应在式(24)后添加轴承阻力项，并将式(24)写为

(26)

式中，Cb为轴承等效阻尼系数，数值应由试验确定。

4.2 阻尼器耗能性能

在阻尼油箱中加入阻尼油并将阻尼圆盘安装于转轴上。阻尼圆盘在阻尼油中转动起到剪切阻尼油的作用，并且由于阻尼圆盘同时具有一定的惯质，也会同时起到提供负刚度的作用。在油箱有油且安装位置为L/6时，一阶振动试验力-位移曲线与理论计算力-位移曲线分别如图7(a)和图7(b)所示，试验力-速度曲线与理论计算力-位移曲线分别如图7(c)和图7(d)所示。二阶振动试验力-位移曲线与理论计算力-位移曲线分别如图8(a)和如图8(b)所示，二阶振动试验力-速度曲线与理论计算力-速度曲线分别如图8(c)和如图8(d)所示。

图7 一阶振动试验与理论曲线Fig.7 First mode vibration test and theoretical curve

图8 二阶振动试验与理论计算滞回曲线Fig.8 Second mode vibration test and theoretical calculation hysteresis curve

在图7(b)和图8(b)中按照式(25)和式(26)所计算的未修正力-位移曲线，其包络面积与实测值图7(a)与图8(a)的力-位移曲线包络面积近似相等，但是其斜率有一定差距。究其原因，是因为试验中阻尼油具有一定的黏度，除了表现出与普通黏滞阻尼器一样的黏滞特性，还会一定程度上附着在阻尼圆盘上随着圆盘一起转动。与当前研究中剪切型阻尼器所体现出的正刚度特性不同[36-37]，现有剪切型阻尼器的剪切板插入阻尼介质中的面积，是随着拉索振动而变化的，在剪切板不断“插拔”于阻尼介质时，由于阻尼介质的密度、油缸内的气体压强等原因，均会使阻尼器表现出正刚度特性。而本文所提出的惯质黏滞阻尼器，阻尼圆盘一直浸没在阻尼油中，附着在圆盘上的阻尼油，以固定质量的形式与圆盘的惯性质量一同起到负刚度的作用。因此需要对式(25)的负刚度项进行修正，负刚度项修正表示为

(27)

式中，k为随动的阻尼油所产生的负刚度，数值应由试验确定。图7(b)和图8(b)中的力-位移曲线，是按阻尼项式(26)和负刚度项修正式(27)叠加所得到的滞回曲线，与试验所得的滞回曲线包络面积与负斜率均相等。

对阻尼器齿条端部的位移数据进行微分得出阻尼器齿条端的速度，绘制阻尼力-速度曲线图7(c)和图8(c)。试验力-速度曲线图7(c)和图8(c)与理论计算力-速度曲线图7(d)和图8(d)吻合较好，理论计算的力-速度曲线为椭圆曲线，由惯质元件与阻尼元件出力叠加所得。未修正的力速度曲线的包络面积，与实测力速度曲线的包络面积有一定差距，同样是由阻尼油所产生的负刚度导致的。而阻尼元件所得的力-速度曲线在图7(d)和图8(d)中为一条斜线，说明在测试的频率与振动幅值下，由阻尼圆盘切割阻尼油所产生的阻力是线性的。因此，包含轴承阻尼项及负刚度项修正的阻尼力的计算公式为

(28)

式中：bd为运动部件产生的惯质；cd为折算后阻尼元件提供的阻尼系数，惯质系数和阻尼系数可分别表示为

(29)

(30)

4.3 拉索-惯质黏滞阻尼器系统减振效果分析

目前，可以通过分析拉索自由振动的衰减速度，来考察阻尼器对拉索振动影响，其评价指标是模态阻尼比或与其相应的对数衰减率[38]。通过采集环境激励下拉索的振动数据，识别出实际拉索的前几阶振动频率，以对应的频率进行人工激振，依次激励起对应阶模态振动。在拉索振动幅值达到一定值后停止激励，令其做自由衰减振动[39]。首先对未安装阻尼器无控拉索的自由衰减振动，是识别试验拉索内阻尼的最便捷途径。通过无控拉索的衰减时程曲线得到拉索内阻尼黏性系数Cc[40-41]，拉索的无量纲内阻尼系数近似为0.013。而后将阻尼器安装于拉索之上，进行受控拉索的自由衰减振动试验。

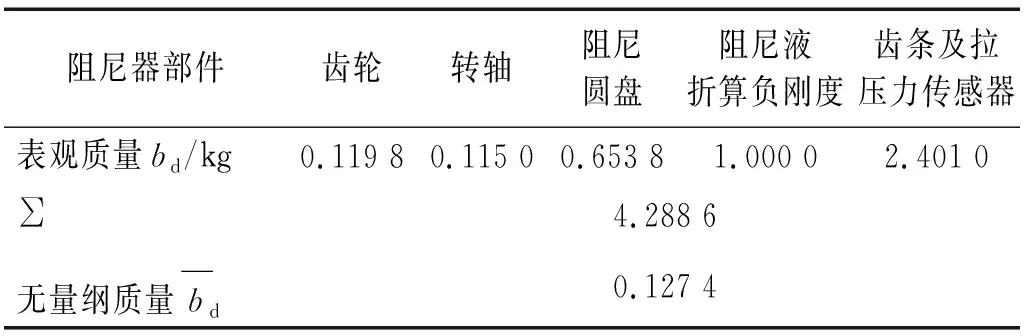
表3 阻尼器惯质参数Tab.3 Damper’s inertial parameters

表4 阻尼器阻尼参数Tab.4 Damper’s viscous parameters

在本文试验中，拉索受控振动条件下，对试验采集的时程曲线进行指数函数拟合。通过对拉索阻尼器安装位置处时程曲线的曲线拟合可以求得拉索发生一阶振动与二阶振动时的阻尼比。同时，在拉索另一端，阻尼器安装位置的对称点处安装激光位移计，测量对称点处的时程曲线。通过比较阻尼器安装位置和拉索另一端对称点的振幅，可以观察到拉索-惯质黏滞阻尼器系统的位移放大效应。对式(11)进行特征值分析，其特征值λi为n对共轭复数，特征向量ψi为n对共轭复向量，特征值可表示为

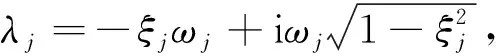
(31)

据此，通过状态空间式(11)得到拉索模态阻尼比理论计算值ξj为

(32)

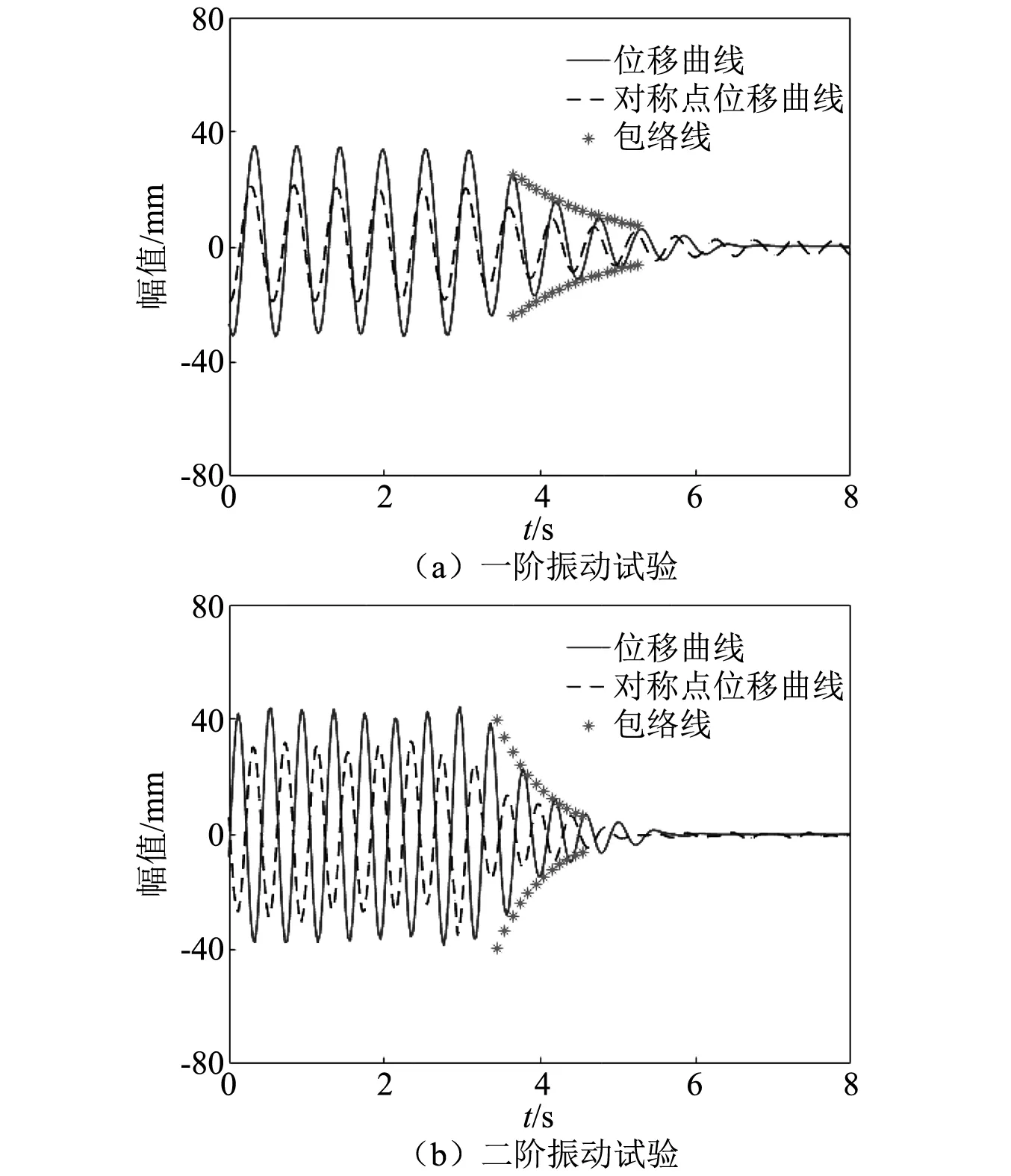
图9 试验时程衰减曲线Fig.9 Vibration attenuation curve

表5 阻尼比结果汇总及误差Tab.5 Damping ratio results summary and deviation%

4.4 振型分析

图10 拉索振型Fig.10 Cable’s mode shape

5 结 论

通过对惯质黏滞阻尼器的理论分析及性能试验可知：

(1) 本文制作的惯质黏滞阻尼器能够有效地抑制拉索的振动，提高拉索的模态阻尼比，使拉索振动迅速衰减。

(2) 将改进Galerkin方法用于惯质黏滞阻尼器的分析是可行的。相比于复模态分析法，改进的Galerkin方法在求解过程中不依赖迭代初值的选取，可有效避免因迭代初值选取不合适而导致的计算结果错误。

(3) 惯质黏滞阻尼器的齿轮、齿条、转轴和阻尼液都表现出了一定的负刚度特性，其对阻尼性能的影响不可忽略，应通过试验测得并考虑在计算模型中。

(4) 惯质黏滞阻尼器的负刚度特性所导致的位移放大作用，对拉索减振有着明显的正面作用，这说明惯质黏滞阻尼器在拉索减振中有着广泛的应用前景。

在下一步研究中，将开展针对垂度拉索的高阶广谱惯质最优化和阻尼最优化方法研究，并进行试验验证。