浅析创新意识的培养措施

何三元

创新意识是指因客观需要带来的一种不安于现状的心理状态，这种心理为创新意识的形成与创造能力的发展奠定基础.处于这种状态的人，思维不被定势或世俗偏见所束缚，常能开辟思维，标新立异地想出或做出常人所不敢想、不敢做的事.教学中，教师应想尽一切办法激发学生的主体意识，通过各种手段培养他们的求异、探索与创新精神.

1 注重实操，知识迁移

新课标一再强调学生的主体性地位，实际操作能有效地推动学生的探究欲，让学生对知识产生探索的兴趣.迁移是指原有认知与经验对新学知识的影响，为了实现知识的正迁移，我们可在实操中充分发挥原有知识的范例作用，让学生在对照、类比中找出知识间的关系，达成知识的迁移.

案例1“圆和圆的位置”的教学

师：大家还记得点与圆的位置关系有哪几种吗？

生1：点在圆内、圆外、圆上共三种关系.

师：很好！那么直线与圆的位置关系呢？

生2：有相交、相离与相切.

师：大家还记得这种位置关系的来源吗？

生3：有两种方法.①将圆固定，通过移动直线，观察二者的交点而来；②固定圆的位置，将直线绕某点进行旋转，观察可得.

师：非常好！点、直线与圆的位置关系都可用数量关系来衡量.那么，圆与圆的位置能用数量来判断吗？这是我们今天要探讨的主要问题.

实践活动：

如图1，取出事先准备好的两个透明的圆，固定其中一个，将另一个慢慢向固定的圆移动，观察它们的位置关系.

生（总结）：通过观察，根据它们的交点分析，有外离、外切、相交、内切、内含五种位置关系.

师：这五种情况若按交点的数量来分，可以怎么分？

（学生讨论）

生4：外离和内含（无公共点），为相离；外切与内切（都唯有一个公共点），为相切；含有两个公共点的为相交.

师：谁能说说生活中存在的与此相关的例子？

生5：自行车前后两个轮胎是外离的两个圆，将两个足球靠在一起放，呈外切的关系.

生6：奥迪汽车的车标为圆与圆相交的关系……

该教学过程首先进行了旧知的回顾，并以此引出新的话题.实践活动的开展，给学生提供了直观形象的感官认识，学生通过观察获得知识的内涵.随着课程的推进，教师让学生借助生活实例深化对此知识点的认识，从真正意义上实现了知识的迁移.学生的创新意识在温故知新、操作实践与知识迁移中得以有效地发展.

2 发扬民主，思想转化

陶行知先生认为：“民主是创造力形成的基本条件.”学生各有自身独特的特征与思维模式.教师应创设民主的学习环境，让学生在舒适、放松的状态下勇于表达自己独特的见解.发扬民主，大胆展示，能促进创新意识的形成.

案例2“二次函数的应用”的教学

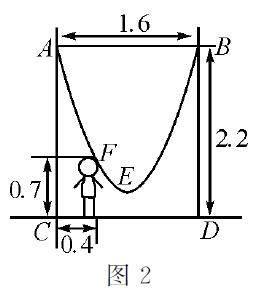
如图2，两根高度为2.2 m的柱子相距1.6 m，一根长绳系于两根柱子的顶端，并垂下.身高0.7 m的小朋友在与立柱相距0.4 m处，其头部恰好与绳子接触，该绳垂下的部分与地面最短的距离是多少？

学生初看题，感到有点懵.此时，需教师适当地引导，以帮助他们找到思考的方向.

师：这根绳子的形状与我们学过的什么很像？

生1：与抛物线很像.

师：很好！既然与抛物线很像，那我们解决问题时可从什么角度去思考？

生2：要研究抛物线，当然离不开直角坐标系.

师：非常好！大家来说说你们各自的想法.

在教师的引导下，学生主动担任起了“解说员”的职责，通过不同建系方法的演示，提出不同的解决方案.在多种方案下，笔者让学生自主交流与争辩，寻找出最简便的解题方法.对于学生积极、主动的演示、思考与辩论，教师给予充分肯定：少数几位同学敢于冲破思维定式的禁锢，另辟蹊径进行创新性思考，值得我们每个人学习.希望大家在遇到问题时，能突破常规思维，从不同维度去思考、分析.

宽松的环境，自由的空间，能让学生放下一切戒备，积极思考、主动实践，发扬民主精神.此过程，教师需有一颗包容之心，要允许并鼓励学生表达出自己真实的想法.只有让学生敞开心扉，才能实现思想的转化，激发创新意识的形成.

3 积极求异，拓宽思路

弗赖登塔尔认为：“教育就是再创造的过程.”这种理念既弥补了知识形成过程缺乏的弊端，也对教师的教学能力提出了新的要求.求异是再创造的基础，它能有效地开阔学生的视野，发散思维，突破思维定式带来的负面影响，实现创新.为此，笔者常以“变式训练”或“一题多解”等方式，鼓励学生学会从不同视角观察与思考问题.

案例3“多边形的内角和”的教学

为了开拓学生的视野，深化学生对知识的理解，发散思维，笔者针对此教学内容逐层递进地设计了以下教学活动过程.

活动1：

（1）根据三角形的内角和猜想四边形的内角和是多少度？

（2）说说验证猜想的方法.

学生提出以下方法：①测量各个角的度数，并相加；②剪下四个内角并拼接，可得一个周角；③通过辅助线，将原图分割成两个三角形进行计算.

（3）分组合作、探究、论证以上方法是否合理.

（4）汇总各组探讨的结论.

（5）教师小结并强调：添加辅助线，将原图转化为三角形的方式是一种常规方法，这种方法对于图形内角和的分析尤为适用.

活动2：

问题经过以上讨论，我们对四边形的内角和有了认识，那么五、六、七、八边形的内角和怎么求呢？

（1）要求学生独立思考后分组讨论.

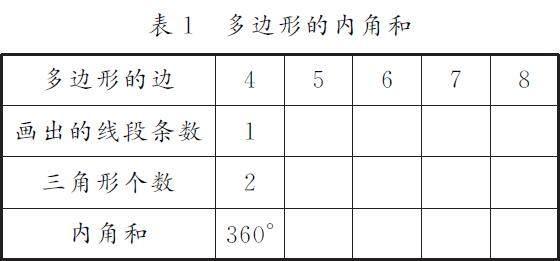
师：根据活动1可知，给四边形添加一条辅助线后，得到两个三角形，获得四边形内角和为180°×2=360°.根据这个规律，大家分组讨论，并将表格1填写完整.

（2）教师参与讨论，以了解学生的真实情况，必要时给予适当的引导与评价.

活动3：

问题遇到求n边形的内角和，应该怎么办呢？

学生从作辅助线，把多边形分解成三角形的角度进行分析，得到以下几种公式：①（n－2）·180°；②n·180°-360°；③180°·（n－1）－180°.

此结论是将任意多边形转化成三角形而得来的.循序渐进的活动，给学生提供了更宽广的想象空间，有效地拓展了学生的思维.学生在多边形内角和的探索过程中，感知并体会到从特殊到一般、数形结合以及模型思想等多种重要的数学思想，这些数学思想的运用为创新意识的发展提供了有力的支持.

当然，创新意识的培养离不想象的支撑.爱因斯坦认为：“想象比知识的学习更有意义，知识具有局限性，而想象却没有边际，社会的进步与发展需依赖想象的驱动.”因此，想象力是实现创造的源泉.案例3的教学过程就是以学生的想象为起点，让学生用各种方法来验证自己的猜想，达到求异的目的.学生切身体会到想象、思考与合作的优势，在教师的积极引导与评价下，有效地激发了学生的创新意识.

总之，创新意识的培养源自课堂的每一个细节，我们虽不能将每个学生都打造成出色的创造者，但创新意识的培养切实可行，这也是所有学生应具备的基本心理素质之一.因此，教师应鼓励学生在思想上、实践上进行创新，并允许一定错误的产生.只有大胆地猜想、尝试、验证，才能实现真正意义上的创新.