调整教学方式 催生精彩课堂

胡松

精彩的数学课堂是在师生互动中激发的思想火花，是在合作交流中生成的灵动智慧，也是在学生活动中的深度学习.精彩的课堂是学生在课堂上的积极思考和主动配合，但是作为学习引导者的教师起着更加关键性的作用，恰当的教学方式可以更好地激发学生的学习热情和主动参与，最大限度地催生课堂的有效生成[1].同样的教学内容和教学环节在不同的课堂上会呈现出不一样的效果，这就是教学方式的巨大作用.我们需要思考什么样的教学方式更加适合学生，更加符合学生的特点，更有利于达成本课的教学目标，教师就应该向着这个方向去努力和调整.下面以“一元一次方程的应用”为例，与大家分享笔者的一些思考和尝试，以供参考.

1 导入——从“创设情境”到“搭台表演”

导入是一节课的开端，俗话说“好的开始是成功的一半”，一个精彩的导入可以迅速抓住学生的注意力，也能使学生快速了解到本课的主要学习内容，做到胸有成足又充满好奇心.創设情境式导入可以让学生找到知识运用的具体背景，迅速产生学习的内驱力，不失为一种导入的优秀方式.然而并不是每一个知识点都能找到比较合适的又符合学生兴趣的情境.我们也可以转换角度，教师搭建平台，邀请学生共同参与到情境创设中去，学生作为主体能够呈现出更加不一样的精彩.

教学片段一：

教师：2021年的东京奥运会上中国运动员们奋勇拼搏，勇创佳绩，在金牌数和奖牌数上都创造了历史，现在老师想和大家一起为此情境编制一道应用题.请看课件——“在本届奥运会上，中国运动员一共获得100枚奖牌，其中金牌数比银牌与铜牌数的和还要多两枚……”我们应该提出什么问题呢？

生1：金牌和银牌数一共几枚？

生2：中国运动员获得金牌、银牌和铜牌各几枚？

教师：两位同学提的问题很好，我们先解答哪个问题呢？

…………

评析：发现问题并主动提出问题是思维发展的重要途径.本片段中通过教师搭建的平台，让学生能主动提出问题并思考问题，在生生互动中感受数学知识的奥秘，体会数学学习的快乐.孔子云：不愤不启，不悱不发.由学生自己主动提问，更能让学生主动求知，之后便能顺其自然地进入新课的学习.

2 过程——变“讲解归纳”为“类比辨析”

课堂的中心环节是新课的展开过程.“一元一次方程的应用”的教学通常会经历例题讲解中的设未知数、列方程、解方程到检验、应用五个步骤.教师借助例题讲解，引领学生进行审题、解题、归纳等环节，基本完成“一元一次方程的应用”的学习.事实上，学生进入到独立思考阶段，对于自己的解题正确与否其实是不太清楚的，因为课堂上对于检验环节基本是忽略的.假若把“讲解归纳”变为“类比辨析”，就能很好地兼顾各个流程，呈现思维的火花.

教学片段二：

师：相信同学们对于“行程问题”的解决已经是游刃有余了.那谁能说出，行程问题主要厘清哪几个数量关系，才能弄懂题意呢？

生3：有时间、路程和速度.

生4：速度=路程÷时间.

师：非常好！那我们看一道题——甲、乙两人分别从相距60 km的A，B两地骑自行车同时出发相向而行.经过120 min两人相遇了，乙的速度比甲的速度慢2 km/h，请问甲乙两人的速度分别是多少？

设乙的速度为x km/h，请问方程应该怎么列呢？

生5：2x+2（x+2）=60.

生6：120x+120（x+2）=60.

师：出现了两种不同的答案，请同学们思考判断一下，并试着求出这两个方程的解.

…………

评析：已知条件中的时间和所求问题的速度单位不同，首先就需要学生仔细地辨析，让学生产生思维的冲突.通过方程的求解，学生计算出120x+120（x+2）=60中x的解为－34，这与实际肯定是不相符的，但是检验之后发现方程的求解也没有问题，再次回到试题中，学生发现原来是时间单位没有进行换算，找到了错误的本质.

本片段教师巧妙地设置“陷阱”，让学生在答案辨析中找到问题，相比于教师的直接告知印象更深刻，效果更好.新的课程改革提出，要关注学生的学习过程，以及数学基本活动经验的获得.基于此，数学知识的获得不仅要通过教师的讲解传授，而更要通过活动的创设，引导学生主动发现和思考，主动辨析和对比，进而产生自己的感悟，内化为自己的认识，才能真正学会学习.

3 运用——变“解决问题”为“活动探究”

数学知识的学习最终要落实到具体的运用当中，只有通过知识的运用，才能检测教学效果.一般课堂的最后环节，教师通过设置问题，来检测学生的知识应用情况，这是一种常见的操作方式.但是这只能检测学生解决问题的能力，实际并不能检测学生运用知识的能力.学生能否将数学知识应用到具体的问题当中，还需要教师能够创设情境，联系生活，考察学生在具体情境中活学活用知识的实践能力.

教学片段三：

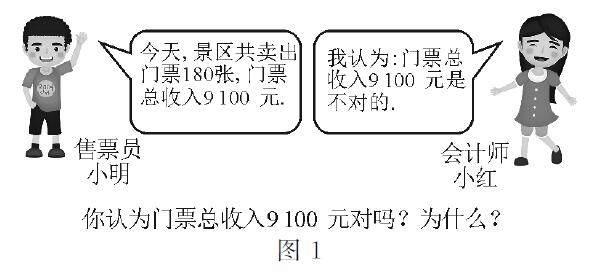
师：通过本课的学习，大家已经熟练掌握了列方程解应用题，但是肯定有同学在质疑学这些有什么用呢？那么下面就要检测一下本节所学的知识在生活中是否用得到？请看材料，如图1.

师：已知梅花洲景区的成人票是儿童票的两倍，成人票每张60元，你们认为上图中的说法正确吗？请小组讨论交流，进行判断并分别说明理由.

…………

评析：本片段是学生较为熟悉的情境，可以体现出数学知识在生活中的应用.为了判断图片中的说法是否正确，学生需要经过列方程进行解答.设成人票卖出x张，根据已知条件可以列出方程60x+30（180－x）=9 100，最后求得x的值为12313，结果不是整数，说明“门票总收入是9 100元”是不对的.另外也可以鼓励学生从不同的角度进行思考，假设成人票的总收入是x元，那么可以列方程180－x60×30+x=9 100，解得x的值为7 400，但是60元一张的成人票，无法通过整数获得7 400元的收入，所以说明“门票总收入是9 100元”是不对的.当然也可以从代数式的角度进行思考，将卖出的成人票和儿童票分别设为a，b张，那么门票总收入就可以列为30（2a+b）元，显然是30的倍数，与总收入9 100不相符，再一次证明了“门票总收入是9 100元”是不对的.

通过这样的问题探究，学生不仅巩固了本课所学的列方程解应用题的知识，而且学会在情境中应用数学知识，并感受到数学的“实用性”.这大大调动了学生的学习热情和积极性，让学生感受到知识的“有用性”，从根本上激发了学生学习的内驱力.

4 教学反思

列方程解应用题对于学生来讲是再熟悉不过的一类题型，但是从小学升入初中在方程的应用问题上还是发生了很大的变化，是一种进阶和递进.因此，教师需要着重帮助学生进行自然过渡，并关注几个问题：（1）初中解应用题属于代数问题，而小学主要是算术问题，教学中要做好学生思维方式的转化和过渡，调动学生学习的积极性；（2）初中应用题由于其复杂性和综合性强，需要学生进行辨析、判断和检验，与小学阶段有较大的区别，教师要引导学生感受检验的重要性；（3）初中应用题与生活的结合更加紧密，需要创设情境感知数学知识的“有用性”.

基于以上三个问题，教学方式也要进行适当地调整，促进教学效果更好地达成.本文中首先通过引导学生主动提出问题，指导学生进行思维方式的过渡；接着在辨析类比中感受检验的重要性；最后通过情境的主动探究，体会到数学知识的“应用”价值，实现了较好的教学效果.

总之，教学方法的适切性是催生精彩课堂的关键.教师只要静心钻研，勇于突破，以生为本，那么数学课堂的精彩就一定在不远处.

参考文献：

[1]鲍建生，周超.数学学习的心理基础与过程[M].上海：上海教育出版社，2009.