基于混合效应的湖南杉木人工林平均高和优势木平均高相关关系模型

杨子铎，李新建，朱光玉，刘洪娜

（1.中南林业科技大学 林学院，湖南 长沙 410004；2.国家林业和草原局中南林业调查规划设计院，湖南 长沙 410014）

在森林调查体系中，树高作为最重要的测树因子之一，是反映林木生长状况的重要指标，也是划分林层和反映立地质量高低的重要依据，也是编制森林经营数表、评估森林生产力的重要参数[1]。在立地质量评价中，林分平均高和优势木平均高是评估林木生长状况的重要指标[2-3]。在人工林或未受人为干扰的林分中，其林分平均高和优势木平均高两者之间的关系极为密切[4]。在营林工作和林分生长研究过程中，有时候需要利用林分平均高和优势木平均高之间的关系互相推算。在森林调查工作中，通过两者之间的关系互相推算，能够节省大量的人力、物力和财力[5]。

目前，对于林分平均高和优势木平均高相关关系的研究较少[6]。根据以往学者的研究，一般认为，在纯林中，两者之间存在良好的线性关系[7-9]。然而以往对于两者相关关系的研究只停留在简单线性与非线性模型阶段，未能考虑到林分平均高与优势木平均高会受到林分年龄、经营措施、立地条件、气候条件、林分密度等多种因素的协同影响与制约[10-12]，因此两者之间的相关关系也可能存在差异。随着近年来数学建模方法的发展，符利勇等学者通过构建混合效应模型有效地解决了传统的建模方法无法反映不同水平或林分因子对树木生长的随机影响,从而导致精度低的问题[13]。混合效应模型由固定效应和随机效应组成，固定效应可以反映整体变化规律，随机效应与总体中不同个体的变化规律有关[14-15]。混合模型的发展与应用，为随机分级数据的拟合提供了可靠的方法，在森林生长与生产收获模型的研究中得到了广泛的应用，取得了较好的拟合效果[16-20]。

杉木作为湖南重要的乡土树种之一，具备速生丰产、经济价值高、材质好等显著优势，是重要的用材树种[21-22]。杉木也是湖南林业生产的重点利用对象，杉木人工林的经营状况直接关系到地区林业产业经济发展，在近几十年湖南人工林的产业发展中发挥了重要作用[23]。通过建立基于混合效应的林分优势木平均高和平均高相关关系模型，可以获得更加精确且符合实际林分优势木平均高和林分平均高数据来评估林地立地质量，对提升杉木人工林的经营水平及林地产量具有十分积极的促进作用。

1 研究区概况

湖南省地处长江中游，三面环山，与多个省份交界。全省年日照时长1 500 h 左右，多年平均降水量在1 450 mm，富含各种资源。土壤主要以红壤和黄壤为主。森林面积1 053 万hm2，活立木蓄积4.61 亿m3，森林覆盖率49.69%，植物种类十分丰富，有水杉Metasequoia glyptostroboides、银杉Cathaya argyrophylla、单性木兰Kmeria septentrionalis、珙桐Davidia involucrata、伯乐树Bretschneidera sinensis等国家重点保护植物。

2 材料与方法

2.1 数据来源

数据来源于湖南省常德、零陵、衡阳、郴州、益阳等五个地区所设置的512 块杉木人工林临时样地。样地大小为20 m×20 m，对于胸径不小于5 cm 的林木进行每木检尺。样地调查内容包括如树高、胸径等基本测树因子和海拔、坡位、坡向、坡形、土壤类型、土层厚度、土壤松紧度等立地因子。对每一块样地的数据进行预处理，求得每个样地的株数密度及样地内林木的平均胸径、林分平均高，找出每个样地平均标准木，通过生长锥钻取标准木，得到林分的平均年龄（Age），每块样地选取3～5 株最高优势木，求得林分优势木平均高（HT）。将所调查的512 块杉木人工林样地数据按照4∶1 的比例分为建模数据和检验数据，分别用于检验和建立平均高-优势木平均高模型。将各样地林分平均高、林分优势木平均高以及调查因子数据汇总列表。

2.2 研究方法

2.2.1 林分调查因子分级方法

为了更方便划分立地类型和构建模型，将海拔、坡形、坡向、坡位、坡度、土壤厚度、土壤类型和土壤松紧度等立地因子和株数密度、林分年龄进行分级处理，以《中国森林立地》[24]为标准，具体标准如下：

表2 调查因子等级划分Table 2 The division of investigation factors

2.2.2 显著性因子筛选

数量化方法Ⅰ是指在自变量中同时包含定量化因子和定性因子的“回归”模型。表达式如下：

由于立地因子和测树因子对林分平均高与林分优势木平均高的影响程度不同，故本研究将林分优势木平均高和林分平均高之比定义为高比值，以高比值为因变量，运用ForStat 统计之林软件进行数量化方法Ⅰ分析，筛选出对高比值影响显著的因子。

2.2.3 立地类型的划分

为了简化线性混合效应模型的构建及进一步提高模型的模拟精度，通过使用Forstat 筛选所得到的显著性因子为对象，根据《中国森林立地》可得到显著性因子等级值（每个等级值代表一个水平值），最后通过对显著性因子的等级值进行组合划分，得到立地类型（Site type，简称ST）。

2.2.4 基础模型的确定

目前已有较多研究显示林分优势木平均高和林分平均高之间存在显著的线性关系[7-9]。根据调查数据绘制的平均高-优势木平均高关系散点图见图1。由图1可以看出两者之间呈线性分布，综合以上，故采用固定线性模型作为本次研究的基础模型。该基础模型表达式如下：

图1 利用建模数据（A）和检验数据（B）得到的优势木平均高－平均高关系Fig.1 The HT-HD plot of calibration (A) and validation (B) subsets

其中，HTi为第i块样地林分优势木平均高，作为模型的因变量，HDi为第i块样地林分平均高，作为模型的自变量；a和b为该基础模型的待估参数，e是误差项。

2.2.5 线性混合模型

根据随机效应因子的数量，线性混合效应模型（LME）分为两种基本形式：单水平和多水平。本研究即是基于单水平线性模型即仅包含一个随机效应因子来构建平均高-优势木平均高关系模型，其一般表达式为[25]：

式中：y是观察值向量，β是固定效应参数向量，α是随机效应参数向量，矩阵X和Z是设计矩阵，分别对应着固定效应和随机效应，ε是误差向量。

在构建线性混合模型时，首先要进行混合效应因子的选取：将筛选出的影响显著的立地因子进行分级组合，构成立地类型（ST）；再将立地类型（ST）通过k-means 聚类成立地类型组（STG）；然后将立地类型（ST）、立地类型组（STG）与其他影响显著的因子分别作为固定效应或随机效应加入到基础模型中，构建混合效应模型。

2.2.6 模型评价与检验

为了准确评价模型的拟合效果，本研究利用赤池信息准则（AIC）、贝叶斯信息准则（BIC）、平均绝对误差（MAE）、确定系数（R2）、均方根误差（RMSE）对模型进行检验与评价。

式中：yi为第i个样本实测值，为第i个样本估计值，为平均实测值，n为样本数，k为模型参数个数，L表示模型极大似然函数值。其中：AIC和BIC 的值越小，则表示模型的拟合效果越好，MAE 和RMSE 的值越接近0，R2的值越接近1，则表示模型的精度越高[26]。

3 结果与分析

3.1 基础模型构建

基于建模数据，利用R 软件对基础模型（2）进行拟合，其拟合结果见表3：

由表3可知基础模型具体形式为：

表3 基础模型拟合结果Table 3 Fitting results of basic model of average breast diameters

3.2 混合效应因子构建

由数量化方法Ⅰ筛选对高比值（林分优势木平均高和林分平均高之比）影响显著的因子。以高比值为因变量，以测树因子和立地因子为自变量，对影响高比值的因子进行筛选。显著性分析结果见表4。根据方差分析表中的“P＞F”值，对立地因子进行筛选，当“P＞F”的值大于0.05即可认为该因子对高比值影响不显著，否则影响显著，从而确认主要影响因子。

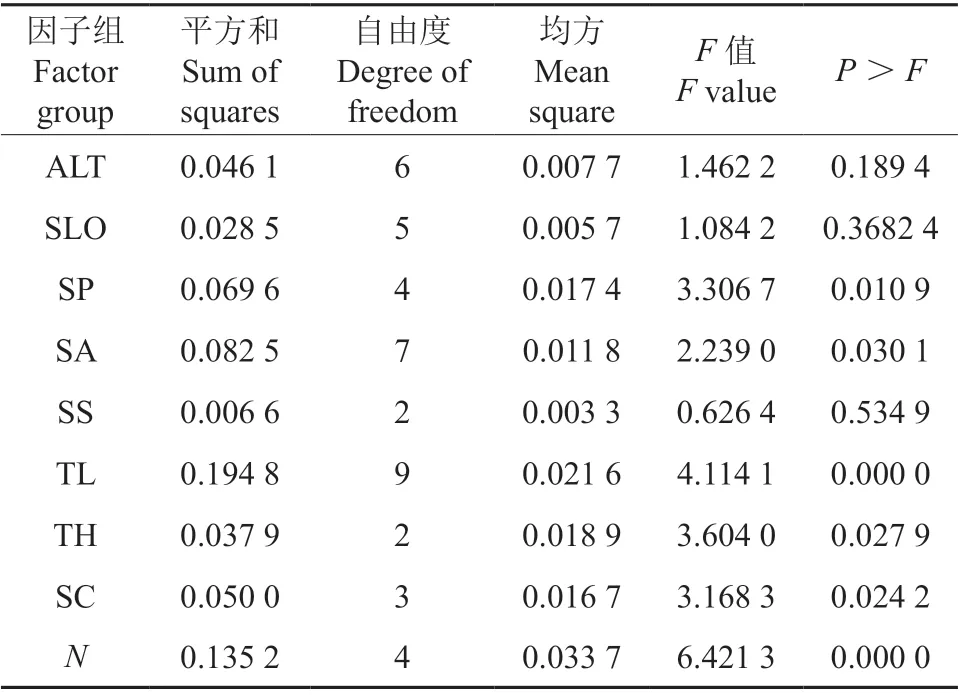
表4 调查因子的显著性检验†Table 4 Significance test of investigation factors

由表可知坡位（SP）、坡形（SS）、土壤类型（TL）、土壤厚度（TH）、林分密度（N）和土壤松紧度（SC）对高比值的影响显著。其中影响显著的立地因子通过组合可将512 个样本划分为322 个立地类型（ST）。

3.3 线性混合效应模型构建

3.3.1 添加立地类型作为随机效应

考虑不同立地条件下，林分树高生长可能存在差异，平均高和优势木平均高相关关系也可能存在差异。基于基础平均高-优势木平均高模型（2），对模型参数a、b的不同组合位置引入立地类型（ST）作为随机效应；引入之后对模型进行拟合，并将结果汇总于表5、6。

根据表5、6 中的评价指标可以得知，将随机效应立地类型（ST）加入到基础模型中后，模型的精度有所提高，赤池信息量（AIC）、贝叶斯信息量（BIC）都有所减小。将随机效应放在参数b上时，确定系数R2由0.790 1 提高到0.914 3，精度提高了15.72%，平均绝对误差（MAE）和均方根误差（RMSE）均有下降，其中MAE 由0.8347下降到0.544 0，降低了34.82%，RMSE 由1.062 1下降到0.685 9，降低了35.41%；将随机效应同时放到参数a和b上时，R2由0.7901 提高到0.836 7，精度提高了5.89%，MAE 和RMSE 均有下降，其中MAE 由0.834 7 下降到0.745 4，降低了10.69%，RMSE 由1.062 1 下降到0.938 4，降低了11.64%，这说明基于立地类型（ST）的混合效应模型明显优于基础模型。因此确定的模型形式如下：

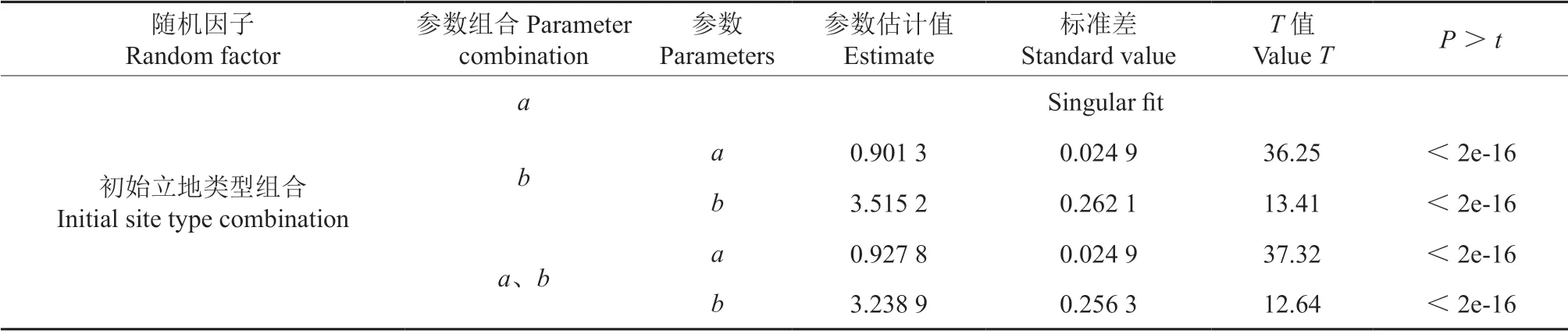
表5 基于立地类型的线性混合效应模型参数估计†Table 5 Parameter estimation of the linear mixed effect model based on site type

式中：HTi为第i个立地类型（ST）的林分优势木平均高，HDi为第i个立地类型（ST）的林分平均高，bi为立地类型（ST）效应的随机效应参数，且bi～N(0,Ψ1)，Ψ1为立地类型（ST）随机效应参数的设计矩阵；εi为第i个立地类型（ST）的误差项。

表6 混合模型的评价与检验统计Table 6 Statistics of fitting and validation for the mixed model

3.3.2 添加立地类型组作为随机效应

1）立地类型组合聚类

立地类型（ST）过多则不便于混合模型的实际应用，为了简化立地类型（ST）组合数，将混合模型（10）拟合的随机效应参数值利用R 软件进行k-means 聚类。聚类精度的标准是确定系数≥0.99，及聚类后的因子信息要包含合并前的因子信息的99%。将随机效应得分值相近的立地类型（ST）合并成立立地类型组（STG）。结果见表7。

由表7可知，当聚为14 类时，聚类精度达到99.0%，达到聚类精度标准。

表7 立地类型聚类结果Table 7 The clustering results of site types

2）基于立地类型组（STG）的线性混合效应模型拟合

根据表8、9 的结果可知：基于立地类型组（STG）的线性混合效应模型的AIC、BIC 相对基础模型及基于立地类型（ST）的线性混合效应模型均有所降低，R2大幅提高。其中，立地类型组（STG）作为随机效应加在参数b上面的混合效应模型R2最高，相对于立地类型（ST）作为随机效应加在参数b上面的混合效应模型（10），R2由0.914 3 提高到0.943 5，精度提升了3.19%，MAE 和RMSE 均有所下降，其中MAE 由0.544 0下降到0.384 9，降低了29.25%，RMSE 由0.685 9下降到0.551 1，降低了19.67%；相对于基础线性模型(2)，确定系数R2由0.790 1 提高到0.943 5，精度提升了19.41%，MAE 和RMSE 均有所下降，其中MAE 由0.834 7 下降到0.384 9，降低了53.89%，RMSE 由1.062 0 下降到0.551 1，降低了48.11%。由此可以看出立地类型组合聚类后，一方面简化了模型的应用，也提高了模型精度。由此确定的模型形式如下：

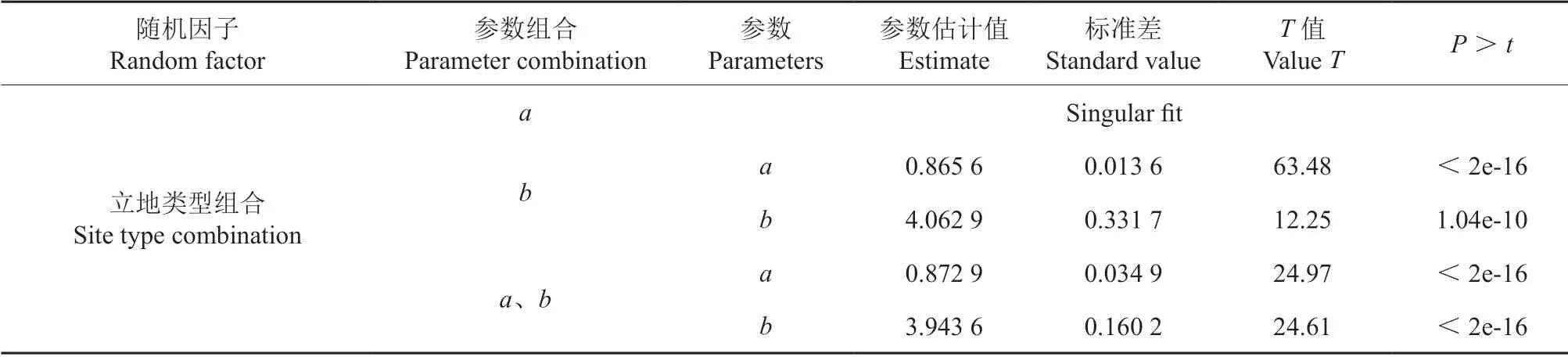
表8 基于立地类型组合的线性混合效应模型参数估计Table 8 Parameter estimation of the linear mixed effect model based on site type combination

式中：HTj为第j个立地类型组合（STG）的林分优势木平均高，HDj为第j个立地类型组合（STG）的林分平均高，bj为立地类型组合（STG）效应的随机效应参数，且bj～N(0,Ψ1)，Ψ1为立地类型组合（STG）随机效应参数的设计矩阵；εj为第j个立地类型组合（STG）的误差项。

表9 混合模型的评价与检验统计Table 9 Statistics of fitting and validation for the mixed model

3.3.3 添加林分密度和林分年龄作为固定效应

将立地类型组（STG）作为随机效应添加到模型中使模型精度显著提升，为了探究密度效应以及能否进一步提升模型精度，在模型（11）的基础上添加林分密度（N）作为固定效应，为了探究不同年龄的林分中两者的相关关系是否存在差异，我们也将林分年龄（a）作为固定效应加到模型上。考虑固定效应间的交互作用，共有6 种模型形式，结果见表10。

表1 林分调查因子统计Table 1 Statistics of the stand investigation factors

根据表10结果可以看出，在混合效应模型（11）基础上添加了固定效应后，模型的R2仅有微小的提高，其中，同时考虑了林分密度（N）、林分年龄（a）及固定效应间交互作用的模型R2（0.944 7）最高，相对于模型（11）R2由0.943 5 提高到0.944 7，精度提升了0.13%，MAE 和RMSE 无明显变化，AIC、BIC 均有变高，说明含固定效应的混合效应模型相对于只含随机效应的模型（11）精度并无明显提升，也说明株数密度和林分年龄对林分平均高和优势木平均高的相关关系无明显影响。为了简化模型和实际应用考虑，选择模型（11）为最优模型。

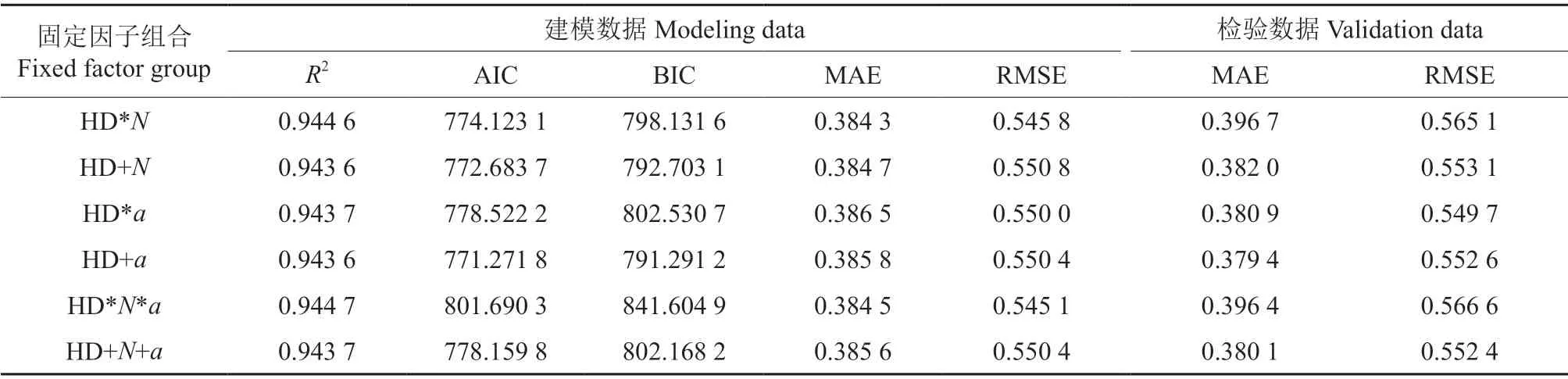
表10 含固定效应的模型评价指标†Table 10 Model evaluation indexes with the fixed effect

3.4 模型精度及适用性检验

为了更加直观地观察基础模型与混合模型的拟合效果，以建模数据和检验数据分别建立优势木平均高残差分布图以及林分优势木平均高预测值与实测值的相关关系图，如图2～3 所示。

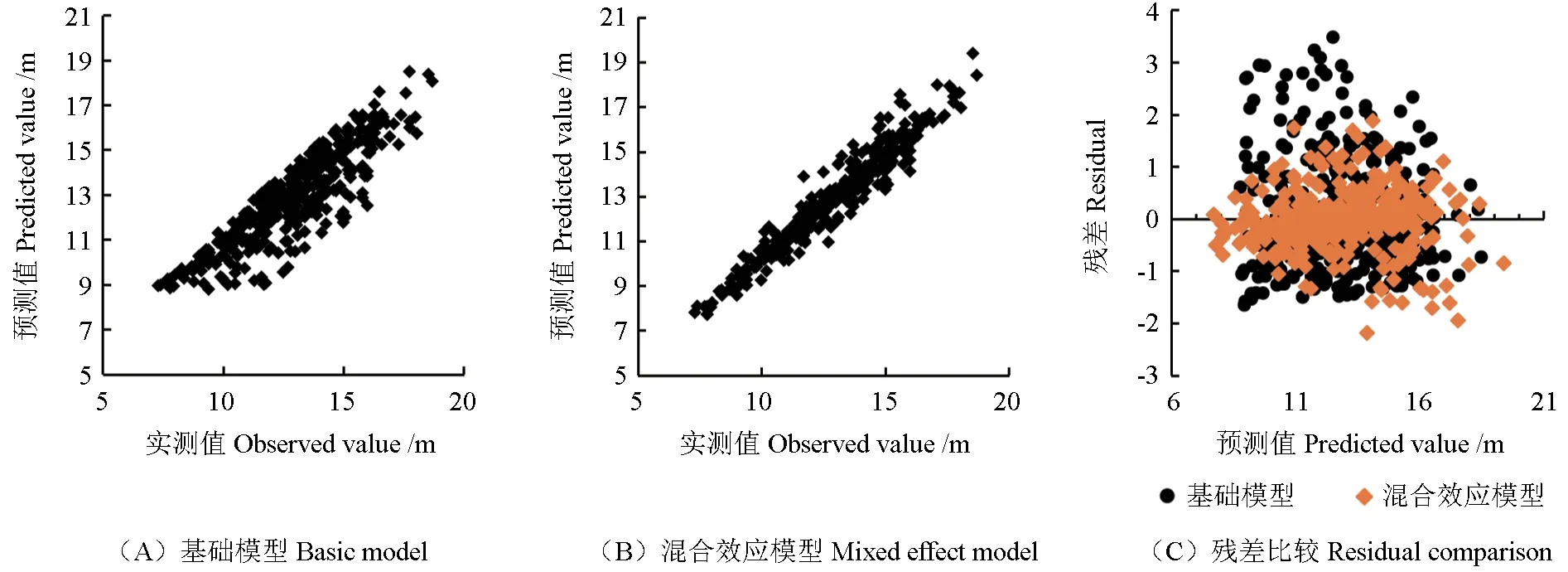
图2 基于建模数据的基础模型与混合效应模型实测值与预测值的相关关系及残差比较Fig.2 Correlation and residual comparison between the measured and predicted values of the basic model and the mixed effect model based on the modeling data

图3 基于检验数据的基础模型与混合效应模型实测值与预测值的相关关系及残差比较Fig.3 Correlation and residual comparison between the measured and predicted values of the basic model and the mixed effect model based on the test data

由图2～3 可知，相对于基础模型，混合模型的优势木平均高预测值及实测值离散程度更小，且混合模型的残差更加集中地分布在X 轴两侧。

综上所述：基于立地类型组随机效应的模型可以极大地提高模型精度，同时利用K-means 聚类划分立地类型组（STG）的方法，可以进一步提高模型模拟精度且解决了复杂立地条件下的模型使用问题。

4 结论与讨论

4.1 讨 论

4.1.1 立地条件、林分密度和林分年龄对林分平均高和优势木平均高相关关系的影响

立地条件、林分年龄和林分密度是影响杉木生长发育的重要因子，在同一树种的前提下，林分平均高和优势木平均高生长模型的预测结果随立地条件、林分密度和林分年龄的不同而出现了明显的差异性[10-12]，因此林分平均高和优势木平均高相关关系也可能不同。

本研究以高比值作为因变量，利用数量化方法I 对可能影响高比值的因子进行筛选。研究结果表明，坡位（SP）、坡形（SS）、土壤类型（TL）、土壤厚度（TH）、土壤松紧度（SC）和林分密度（N）对高比值有着显著的影响。这与王忠诚等的研究结果部分一致，都认为立地因子会对高比值产生显著影响，合理考虑立地因子可以提高模型精度[6]。但以往的研究未能考虑到林分密度和林分年龄对林分平均高和优势木平均高相关关系的影响，本研究尝试性地以林分密度（N）和林分年龄（a）为固定效应、以立地类型组（STG）为随机效应构建线性混合模型，通过AIC、BIC、MAE和RMSE 等检验指标可知含林分密度（N）和林分年龄（a）的混合模型相对于只含立地类型组（STG）的混合模型精度并无明显提高，这也说明在不同密度、不同年龄的杉木林分中，林分平均高和优势木平均高相关关系是相对稳定的，林分密度（N）和林分年龄（a）对林分平均高和优势木平均高相关关系无显著影响。

由于本研究只采用了湖南省内的杉木样地数据，所以模型的适用范围有限。后续研究中，希望通过增加样本量来提高说服力。另外本研究只考虑了立地类型、林分年龄和竞争对高比值的影响，林分的高生长可能还受其他因素的影响，如气候因子、土壤因子、林分空间结构、林分类型等。所以，还可以进一步探讨其他因素的影响，进一步优化模型。

4.1.2 线性混合模型对构建林分平均高和优势木平均高相关关系模型的影响

构建线性混合效应模型可以有效地解决传统的建模方法无法反映不同水平或林分因子对树木生长的随机影响的问题[27]。在确定基础模型之后，构建线性混合模型，期望能得到湖南省杉木林分平均高和优势木平均高的相关关系。通过比较其AIC、BIC、R2、MAE 和RMSE 等评价指标，AIC、BIC、MAE 和RMSE 值越小、R2值越大，则模型拟合效果越好[27]。研究结果表明：基于立地类型组（STG）的线性混合模型（11）相对于基础模型（2），R2大幅提高，AIC、BIC、MAE 和RMSE 等均有明显降低，这说明基于立地效应的线性混合模型明显优于基础模型。线性混合模型不仅能反映总体优势木平均高估计，也可以通过方差协方差结构校正随机效应参数，以此来反映样地立地条件之间的差异，所建立的混合模型能对优势木平均高数据进行更准确的估计。

4.1.3 k-means 聚类对构建林分平均高和优势木平均高相关关系模型生长模型的影响

本研究结果表明，依据立地类型这一主导因子，可将湖南杉木人工林划分为14 个立地类型组合，由于初始立地类型组合类型数过多，不利于混合模型的有效应用。为了简化，本文将初始立地类型（ST）应用到模型（10）拟合的随机效应参数值进行k-means 聚类。以聚类精度≥99%为标准，将322 个立地类型（ST）聚成14 个立地类型组（STG）。构建基于聚类的线性混合效应模型，利用AIC、BIC、R2、MAE 和RMSE 等5 个评价指标进行模型评价，并与基础模型、初始立地类型拟合结果进行比较分析。结果表明，聚类后的线性混合效应模型精度明显提升。充分说明构建基于聚类的线性混合效应模型可以提高线性混合效应模型的实用性。

4.2 结 论

本研究采用数量化方法Ⅰ、线性混合效应模型、k-means 聚类等方法首次构建含立地效应的湖南杉木人工林林分优势木平均高-林分平均高模型。得出如下结论：1）坡位（SP）、坡形（SS）、土壤类型（TL）、土壤厚度（TH）和土壤松紧度（SC）是影响高比值（林分平均高与优势高均高之比）的显著性因子。2）构建混合效应模型可以显著提高建模精度，其确定系数（R2）从0.790 158 提高0.914 348。3）构建基于聚类的线性混合效应模型可以进一步提高建模精度，其确定系数（R2）从0.914 348 提高到0.943 512 8。4）添加林分密度（N）和林分年龄（a）作为固定效应对模型精度提升不明显。本研究首次提出了含立地效应的林分平均高和优势木平均高混合模型，从模型的角度客观地解释了立地条件对杉木人工林平均高和优势木平均高相关关系的影响规律，为湖南杉木人工林的可持续经营与立地质量评价提供了理论支撑。