板材U形弯曲成形理论及有限元仿真分析

夏建生，窦沙沙

（盐城工学院机械工程学院，江苏 盐城 224051）

1 引言

在近代工业急速发展，板料成形技术已成为精密机械产业中降低成本不可或缺的方法。CAD/CAE软件应用，在计算机上设计建立模型，并利用其高速运算能力进行数值分析来模拟加工情况，可缩短设计时间，比以往实作来试验产品制造的可能性，大大降低成本，缩短产品生命周期，提高精度，提升产业竞争力。其他普遍应用于日常生活以及工业科技发展，如手术器械、运输工具、运动休闲器材、3C产品等相关技术至今已应用于医院、医疗器材，且随需求日益增加[1]。金属板材成形过程的数值模拟是一项复杂的研究工作，主要因素有：高度的几何和材料的非线性关系，模具的作用造成工件大位移、大旋转、大应变所造成几何上的非线性运动行为，包含金属材料的机械性质、模具与材料的摩擦、成形速度以及温度等因素的影响[2]。

板料弯曲是将板材加压弯曲成一定曲率、角度与形状的加工法，是板材成形领域常采用的加工技术，被大量应用于汽车零件、机械结构材和零组件等各种相关工业制品及家电用品上，常见的弯曲有V型、U型及L型等。板料弯曲过程中容易产生变薄、增厚或翘曲变形等问题，无法精确的获得想要的形状。文献[3]以镀锌板为对象，发现U型弯曲过程中，考虑摩擦因素下的回弹量和侧壁卷曲的现象与模具半径、模具间隙、加工硬化率和屈服强度成正比。文献[4]使用有限元素程序分析U形弯曲工艺参数，凸模速度，惩罚函数，阻尼比等，结合正交实验评估影响回弹量的重要因子，结果得知板材元素大小和圆角半径为显着因子。

文献[5]用NUMISHEET93分析U型弯曲成形问题，分析弯曲后的回弹量，结果发现变化的压料力可以获得较佳的成形品质。文献[6]用增量弹塑性大变形有限元法分析V型弯曲，模拟回弹及马鞍现象，获得较好的效果。在增量弹塑性大变形有限元理论研究的基础上，研究金属板材U型弯曲过程工艺参数对成形性能的影响，改善成形中的厚度变化及翘曲现象，并用实例验证，探讨相关的改善方法。

2 板料成形理论

2.1 虚功原理

以Cauchy 应力的Jaumann 微分作为构成关系式的应力率，用更新的拉格朗日公式描述弹塑性变形，求得应力应变的虚功原理，如式（1）所示。

式中：—应力σij的Jaumann微分应变率应变张量；虚拟应变率；δLij—虚拟位移；δνi—虚拟速度；f—表面力；V—单位体积单位体积力；S—单位表面积。

2.2 弹塑性本构方程

假设材料具有均匀性与等向性；成形过程不考虑温度变化影响；材料遵守Von Mises屈服法则，在弹性区域内满足胡克定律，在塑性变形时遵守Prandtl Reuss流动法则；受等向性应变硬化影响，应变包括弹性应变和塑性应变两部分，凸模、模具及板材视为刚体；反向卸载不考虑包辛格效应。经过上述假设，本构方程可表示为：

式中：—σij的Jaumann 微分；—弹塑性张量；—总应变率；—弹性模量；f—Von Mises屈服函数；H′—应变硬化率—等效应力。

的矩阵形式表示为：

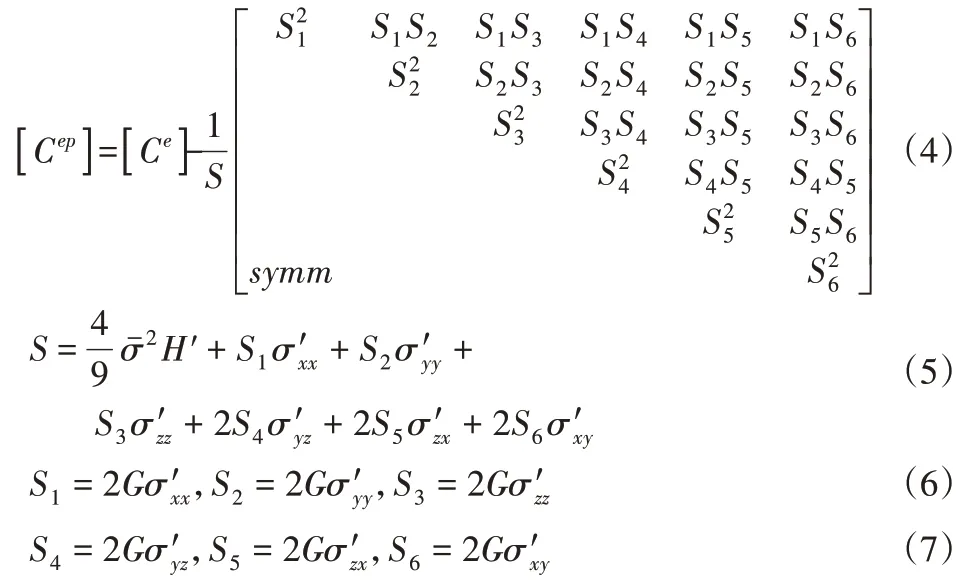
式中：E—弹性模量；ν—比泊松比，当α=1时为塑性状态，当α=0时为弹性或卸载状态。

2.3 有限元分析

有限元分析是将结构离散，划分为多个小单元的方法。基于大变形应力与应力速率关系和更新拉格朗日公式，有限元变形、材料组成关系、各单元的速度关系式为：

式中：[N]—形状函数节点速度；[B]—应变率速度矩阵；[M]—速度梯度矩阵。

本构方程可以用增量形式表示：

式中：[K]—整体弹塑性刚度矩阵；{ΔF} —节点移位增量；{Δu} —节点力增量。

用增量法表示第（i）步的Cauchy应力方程：

2.4 摩擦处理

金属冲压成形中，工件与模具的接触与摩擦为复杂问题，假设滑动时之摩擦是遵照库伦摩擦定律，摩擦相对速度vt分为两部分，可逆（弹性或黏滞）部分与不可逆（塑性或滑动）部分

在弹性时接触应力张量与相对速度间之关系如下：

式中：Et—切线刚性分量；En—法线刚性分量。在摩擦的边界条件下，虚功原理方程式可表示为：

假设摩擦边界采用节点弹簧模型，有限元方程式表示为：

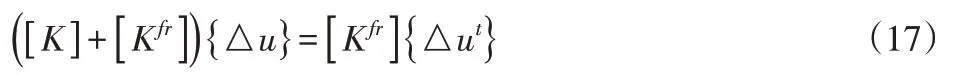
式中：{ △u} 和{ △ut} —节点位移向与模具位移向量；[Kfr]—摩擦刚性矩阵仅存在于与模具接触时的节点自由度。

2.5 rmin增量法

以弹塑性大变形有限元素分析的增量法，在每一次时间增量的过程中，板材成形是以其增量开始的坐标为参考基准，采用更新拉格朗日公式的方法，计算卸荷状态下板料的位移、应变、应力、荷载、回弹值，每一步的荷载增量值由rmin公式进行判断和控制，方程如下：

式中：r1—最大允许应变增量；r2—最大允许转动增量；r3—材料屈服判断；r4—自由节点与模具的接触位置；r5—接触节点与模具的分离位置。

3 数值模拟分析

在弹塑性有限元理论基础上，用NX软件进行前处理，包括模型建构和网格划分；将导出的数据文件导入到自编的金属板材有限元分析程序My−Form分析，分析结果数据导入到NX后处理以图形方式输出，输出内容有凸模负荷、应力与应变、厚度、回弹、翘曲分布等。为了研究不同的工艺参数对成形性能的影响，选取凸模圆角半径、凹模圆角半径、模具间隙等参数进行分析，考察这些参数对应力、应变、壁厚及翘曲的影响，并优化出最佳参数。

3.1 材料参数

实验板料选用中国某钢铁公司提供的汽车结构冷轧板（JIS G3134 2006），其材料性能，如表1所示。

表1 冷轧板材料参数Tab.1 Material Parameters of Cold Rolled Sheet

3.2 有限元模型及网格分割

模型含凸模、凹模及压料圈等三个部分构成。在模拟分析过程中，材料性质设定为等向性材料。首先在NX软件建立模具及板料的三维模型，再利用NASTRAN Meshing工作模块进行网格划分，模具采用三角形元素，假设模具为刚体，受力无变形；板料的网格分割采用四边形四节点退化壳元素，由于板料的几何外形具有轴对称性，取用四分之一分析。

3.3 模拟结果分析

3.3.1 凸模负荷与位移关系

凸模负荷与位移根据行程分三个阶段：第一阶段（0~15）mm，凸模的负荷急剧上升，主要是由于凸模底部端接触到板料并带动向凹模入口处流动变形，导致板料加工硬化增加。第二阶段（15~22）mm时，负荷呈缓慢增加，到22mm时达到最大值，原因是板料在滑入凹模圆角时，板料向下滑动同时向中间集中，造成负荷增加。第三阶段（22~40）mm，板料脱离凹模圆角时，其流动方向向下，板料与凸模前端及凹模侧壁接触，导致凸模负荷随凸模冲程增加而下降。凸模负荷与位移关系，如图1所示。

图1 凸模负荷与位移关系图Fig.1 Relationship Between Punch Load and Displacement

3.3.2 应力分布

板料成形过程中，初始应力主要集中在凸模圆角与凹模圆角处。当冲程H=12mm时，应力集中区域主要在凸模圆角处，板料底部也稍微有应力集中现象。随着冲程的增加，板料与凸模圆角接触区域的弯曲力矩大，产生应力集中现象；部分应力均匀分布于板料侧壁。当冲程H=35mm板料脱离压料板后，翘曲应力集中现象逐渐消除，板料侧壁应力分布均匀。分析各项参数影响对应力影响得出：应力随着凹模圆角半径、随模具间隙和板料厚度增大而增大，凸模圆角半径和摩擦系数对应力影响不大。板料的应力分布，如图2所示。

图2 板料应力分布图Fig.2 Sheet Stress Distribution

在板料整个成形过程中，板料厚度会发生一定的变化。在冲程H=12mm时，板料较容易在凸模圆角半径处产生变薄，而进入凹模过程中，在经过凹模圆角半径时，受模具完全压紧产生摩擦力影响，材料无法顺利流动，其流动方向产生变化，板料会产生向两侧圆角中心处挤压而增厚；当冲程H=20mm板料厚度出现最薄值；当冲程H=35mm时，板料出现增厚现象，最大厚度值出现在板料的两端圆角处。经过分析，各项参数对厚度影响为：变薄区域随凸模圆角半径增大而增大，随凹模圆角半径增大而越小；模具间隙、摩擦系数则对厚度分布影响不大。板料厚度分布，如图3所示。

图3 厚度分布比较图Fig.3 Thickness Distribution Comparison Chart

3.3.3 翘曲分析

在成形过程中，U型弯曲沿着Y轴的翘曲量不同，其变化，如图4 所示。可以看出：翘曲形成最主要是在冲程H=0.0mm 到12.0mm 之间，随后翘曲量增幅减缓。冲程H=9.0mm 时，翘曲量为2.13mm；冲程H=12mm 时，翘曲量为3.64mm；冲程H=40.0mm时，翘曲量为4.70mm；卸载后的翘曲量为4.72mm。翘曲原因是凸模向下移动使板料进入凹模，受到凹模拘束使板料沿着凸模侧壁贴合动作，导致在曲线转折处产生了反向作用力，迫使凸模底部的板料外翻造成翘曲现象。

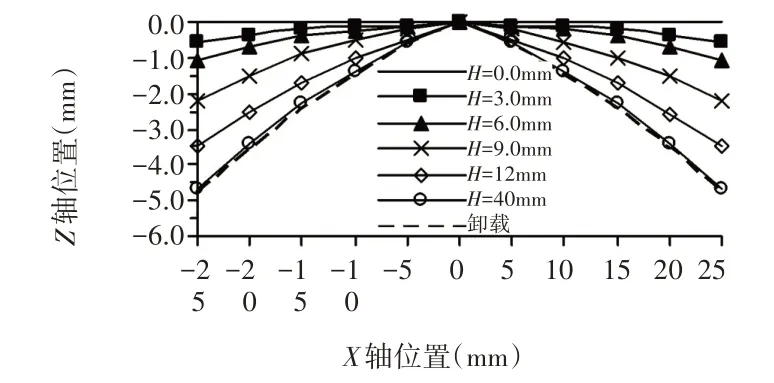
图4 不同冲程下翘曲量图Fig.4 Warpage under Different Strokes

不同冲压参数对翘曲影响：固定凸模圆角半径，凹模圆角半径越小翘曲量越好；固定凹模圆角半径，凸模圆角半径越大翘曲量越小；模具间隙对翘曲影响不大。如图5所示。

图5 翘曲和回弹量分析Fig.5 Analysis of Warpage and Springback Angle

在有限元仿真后，对板料进行了冲压实验测量，在相同的参数下对厚度和翘曲量进行了测量，其中厚度采用尖头式分厘卡，测量板料的长轴方向来测量断面厚度值；翘曲量用游标卡尺测量，如图6所示。通过实验数据的对比，实验与模拟的变化趋势是一致的，其中误差率控制在5%以内，证明了本增量有限元模拟方法的有效性。

图6 产品验证图Fig.6 Product Verification

4 总结

采用Prandtl Reuss流动法则与Von Mises的屈服条件，结合有限变形理论及更新的拉格朗日法建立增量弹塑性大变形有限元素分析，结合四边形四节点退化壳元素所推导的形状函数耦合到刚性矩阵中，以广义rmin法则进行判断，结合U型弯曲进行成形分析，探讨其所产生的翘曲现象，并配合不同的参数获得改善翘曲最佳参数，并进行实验验证结果一致，结论如下：

（1）前段应力主要集中在模具圆角处，随着冲程移动到凹模入口与板料侧壁处，应力分布均匀。应力随着凹模圆角半径、模具间隙越和板料厚度的增大而增大。（2）板料在凸模底部圆角处发生变薄，在板料的长轴末端发生增厚。变薄区域随着凸模圆角半径增大被变薄区域增大、而随凹模圆角半径增大被变薄的区域减小。（3）翘曲通常出现在凸模的圆角与凹模的圆角相切的时候，而后增幅变缓，翘曲应力集中的现象逐渐消除。（4）凸模圆角固定下，凹模圆角越小翘曲量越小；其次凹模圆角固定下，凸模圆角越大翘曲量越小。