电科专业“数学物理方程与特殊函数”课程教学反思

江 贝，陈 雪

（1.湖北大学物理与电子科学学院，湖北 武汉 430062；2.深圳大学微纳光电子学研究院，广东 深圳 518060）

引言

数学物理方程与特殊函数这门课程在电科专业一般是作为一门专业选修课程来开展，课时较短，为32 学时。这门课程连接了基础数学课程和高级专业物理课程，在基础课程和专业课程之间承担了融合衔接的作用。可以说，数学物理方法这门课程是大学生由基础课转向专业课程的必经之路。所以说这门课程是一门很基础但又很重要的课程，也是一门学生难学老师难讲的课程。课堂第一章就会给学生用牛顿第二定律推导出波动方程，推导所需知识点并不难，但是过程有些烦琐，那么老师想要给学生讲清楚方程怎么来的就必须要做公式推导，做公式推导学生就容易觉得枯燥，容易走神。这门课程由于他的课程内容决定了课程从头到尾基本是被推导公式贯彻始终的，而且，最终得到的数学解一般是一个比较复杂的积分加求和的形式，难以和物理的现象进行联系融合，这也是为什么说这门课程老师难讲。那么学生难学则体现在了课程的割裂性上，单独作为一门课程，与专业课程割裂开来，学生不明白学习的意义，同时，由于推导过多，难以集中注意力，课堂中容易走神。其次虽然课程解决的是物理问题，但是面对数学语言，过于抽象，不能很好地与物理现象相互联系。加上课程时长短，内容多，使得老师和学生疲于教与学，课堂上的互动交流比较少，这就导致了这门基础课程被公认为本科阶段教和学难度比较高的课程之一。

1 反思

笔者既作为学生学习过这门课程，也作为教师教授过这门课程，在课程的教学过程中，总结了四点教与学的反思。第一点反思是，第一章的小细节需要讲授得十分透彻，才能让学生更好地理解，后续学习才能够跟上。

对于电科专业的学生，课程内容精简了许多，核心内容为三类方程，四种解法。三类方程指的是波动方程，输运方程和稳定方程。这三类方程已经可以覆盖大部分学生有可能会遇到的物理问题，足够工科学生后期专业课上使用。定解问题是由泛定方程和定解条件组成的，相对于泛定方程的一般规律性，定解条件的具体细节对学生而言是一大挑战。在具体问题具体分析的过程中，学生并不能很好地掌握定解条件。对某一具体的物理问题写出定解条件是最能体现出学生的物理和数学功底的。定解问题主要讨论初始条件和边界条件。初始条件数量对应用于泛定方程中未知函数u 对时间t 的微分阶数。时间t 的n阶方程需要n 个条件，对应到不同的方程中不同物理量会有不同的物理含义。对应到输运方程中，描述的就是初始的温度或者浓度。此处需要特别强调的地方在于，对于稳定场问题，因为物理量并不随时间变化，所以稳态方程中不含有时间参数，所以是没有初始问题的。这个地方需要多对学生进行强调，经常在讲完这一章后，依然会有同学对这个问题犯迷糊。初始条件必须可以描绘整个系统初始的状态，这句话强调了两点。第一点是初始，也就是说初始条件描绘的是t=0 时的系统状态，这个地方需要结合定解问题中位置和时间的取值范围来讲解。例如，对于这样一个定解问题：一弹性杆原长为l，一端固定，另一端拉离平衡位置b 而静止，放手任其振动，请给出定解问题。这个题目的定解问题会写成这样：

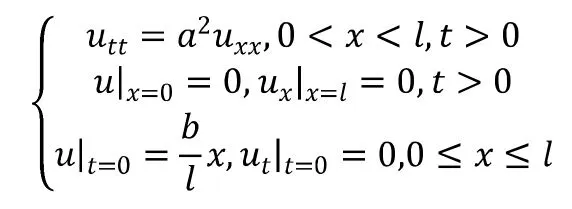
那么初始条件强调一个初始，也就是t=0，那么什么时候t 开始计时就是一个很重要的问题了。这个时间开始计时的时候往往都是课堂讲解中最容易忽略的点，也是最容易使学生犯迷糊的地方。教师在常年的课堂讲解中由于十分熟悉时间t 的概念，再加上这个实际是一个十分小的细节，很容易在课堂讲解中忽略过去，直接告诉学生放手任其振动，这时t 开始计时，但是对于学生而言，这些知识点都是他们第一次学习，这个小细节的忽略很容易造成学生对初始条件的不理解，不明白为什么是放手开始计时，如果换个题干，又该是什么时候开始计时呢？因此，这里需要和学生讲解清楚，时间t 是属于泛定方程的一个自变量，所以时间开始计算的时候应该是物理现象可以用波动方程描述的时候，波动方程是用来描述振动的，那么在这个例题中，这根杆在放手后才开始振动，也就是说，此时波动方程对这个杆的振动才是适用的，所以在放手的同时，属于波动方程的自变量的时间t 开始计时，在放手之前通通属于t=0 的时刻。这也是为什么在定解问题中泛定方程后会跟一个t>0 的时间范围，意思就是满足泛定方程时，开始计时的意思，初始时刻是不满足泛定方程的。第二点强调的是整个系统。这里也是很多同学会在给出初始条件时容易犯的错误。很多同学在给出初始条件时非常容易将位置参数也一起固定下来。实际上初始条件只能固定时间t=0。初始条件强调要描绘整个系统的初始状态，不仅要描述系统内部，也要描述到系统的边界，这一点在例题定解问题的初始条件后的位置参数的范围是有所体现的。很明显，例题中的初始条件给出了t=0 时刻，系统任意位置的某一点的位移和速度，杆有多长，x 可以取多大，包括边界0 和l。对于边界条件也是一样，边界条件只确定了一个变量，即位置，并没有确定时间，此时的时间取值范围要求是在t>0 时刻，也就是说边界条件描述的是杆在振动时的边界情况。但是在课堂教学和书本中，侧重点一般都会倾向于泛定方程和定解条件，方程和定解条件的取值范围并不会进行解释，取值范围出现在书本中实际上是十分突兀的，在定解问题讲完后就直接出现了，十分容易被忽略。实际上，这些对应方程和条件的取值范围对学生理解定解问题是有很大帮助的，它能够很好地帮助学生掌握和理解初始条件和边界条件的注意要点。课堂中，通过将物理问题转化为数学语言，写成定解问题，再将定解问题转化为语言描述的过程中，对应的取值范围描述都是十分重要的，对学生理解物理语言和数学语言的相互转化是有巨大的帮助作用的。所以在定解问题讲完后，教师需要细致地讲解一下方程组中出现的取值范围，将整个第一章定解问题的注意要点都串联起来，来帮助学生理解。

在边界问题上需要给学生讲清楚外法线向量的问题。很多同学在这一部分会搞不清楚什么是外法线向量。法线就是垂直于面的直线，有方向之分。对于立体表面而言，法线是有方向的：一般来说，由立体的内部指向外部的是法线正方向即外法线，反过来的是法线负方向。很多同学没有办法正确区分这个由里指向外，尤其是在后期的格林函数法中，因为辅助函数V 不能使r 等于0，所以要在区域中，以M0 为中心，r 为半径挖去这个球（三维）或者圆（二维）区域。此时，一个实心的区域就变成了一个腔体，这个时候虽然那个挖去的区域在视觉上是在区域内的，但是这个空腔内部的空心区域实际是属于外界区域了，定解问题和辅助函数共同有意义的区域是- 。其他区域全部都属于外界区域，只有- 区域是里，此时空腔内部的边界上的外法线向量应该是由- 区域的里指向空心区域的外，转化为数学语言应该是-r。这个地方是许多学生会出现疑问的地方，需要重点强调清楚。

第二点反思是，不要将课堂时间浪费在给学生补基础上。例如，边界条件，分别为第一类边界条件，第二类边界条件和第三类边界条件。第一类边界条件是未知函数在边界的值，第二类边界条件是未知函数法向导数在边界的值，第三类边界条件是未知函数在边界的值和法向导数在边界的值的线性组合。在边界条件的提出中，会用到物理方面的知识，如在弦振动问题中，弦的一端与弹簧相连，这时就需要用到胡克定律，教师在课堂教学时需要将胡克定律的定义和公式给学生写出来。课堂教学的重点应该集中于数理方程上，课程时间宝贵，不能浪费时间到不属于此门课程的知识点中，此刻就需要教师在课前做好准备工作，在需要的时候直接将物理知识点拿出来让学生使用。再比如二阶常微分方程的通解，实际上学生在高等数学中是有学过对应的课程的，但是由于不经常练习，需要用时，大部分学生都处于不记得的状态，所以这个时候要提前给出通解，让学生记下来。二阶常微分方程的通解，可以说是贯穿着整个分离变量法的。

第三点反思是推导在课堂教学中需要掌握一个度。推导是理解这门课程的重要过程，公式推导在数理方程课程中是必不可少的，但是推导过多又容易导致教学的效果变差，所以推导在教学过程中的比例需要教师自行掌握，要做到张弛有度。如果因为推导枯燥就减少推导内容，很容易导致课程内容衔接不上，学生无法理解。比如第一章的数理方程的引出，如果不进行那一系列的推导，那么方程的提出将会受到很大的质疑，无法与之前的基础衔接上。学生根本无法理解为什么波动方程是一个2 阶偏微分方程。但是如果全是推导，在学生没有提前复习的前提下，大部分学生是无法跟上老师推导的步骤的。而且一个完整的知识点的推导实际上是十分烦琐且步骤很多的，一般是可以写满整块黑板的，这种情况下，跟不上的学生是很容易决定跳过步骤直接背结果，但是跳过不听的结果就是那个结果他看不懂，不知道公式里面的符号到底代表什么，连带着后续的求解他也跟不上。这样子很容易打击学生上课学习的热情和信心，所以老师在教学中要灵活安排推导在课堂教学之中的比例，要控制在能给学生都带到，又不会让学生觉得太难而放弃，这就需要用到教师的教学经验。同时教师也要学会适当地给学生留白，上课不能讲得过分细致，面面俱到很容易导致学生没有重点，失去主动学习的自主能动性。

第四点反思是课堂教学需要一些可视化的东西。课程名叫数学物理方程，说明这门课程属于交叉学科，是数学和物理的一个结合课程。我们需要将物理现象转化为定解问题，然后求解得到数学结果，再将数学结果转化为物理意义。定解问题的解随着边界条件的改变而改变，而且写出来一般会是比较复杂的形式。例如，行波法解决无限域的波动问题时，答案实际上是两个波动方程相加，一个是左行波，一个是右行波。那么为了达到更好的课堂效

果，像这一类的数学解可以采用MATLAB，Mathematica或者COMSOL 等模拟软件来进行可视化展现，毕竟对于物理而言，图像更能生动形象地进行物理结果的展示，数学物理方程解定解问题最终还是要回归到解决物理问题上。通过改变定解条件，得到不同的解，通过图像或者动画更直观地表现出定解条件对物理问题的影响，可以让学生对结果有一个直观深刻的印象，能够更好地将数学和物理结合起来。这就需要老师在课堂外多下功夫多花时间。

2 结语

本文通过对数学物理方法与特殊函数的教授和学习的回顾，总结了四点教学上的反思，希望通过这四点反思来达到更好的课程讲授效果。当然仅仅这四点教学反思还是不够的，课堂讲授效果实际上还可以进一步提升。如何将这门课程讲好，让学生学懂将会是笔者今后一直努力的目标。