OFDM 雷达信号子载波调制方式识别方法

黄章斌，杨荣杰

（解放军75842 部队，广州 510000）

0 引言

正交频分复用（OFDM）雷达作为一种新体制雷达，具有距离和速度分辨率高、频谱利用率高、自相关函数的旁瓣低、抑制多径和杂波能力强、截获概率低等优点，这对OFDM 雷达的电子对抗侦察工作带来了严峻的挑战。对OFDM 雷达信号的子载波调制方式的精确识别，是进行雷达类型识别、战场电磁态势分析和实施电子干扰、反辐射攻击的前提，因而具有重要的现实意义。

文献［3］较早提出了利用平稳随机信号的高斯性和时间可逆性，对OFDM 雷达信号子载波调制方式进行识别，但该方法在低信噪比条件下识别性能不高。文献［4］克服了文献［3］方法抗噪能力弱的缺陷，提出一种基于最大似然函数的OFDM 信号子载波调制方式识别方法，虽然该方法在高斯信道下表现优良，但在多径衰落信道下识别性能则急剧下降。文献［5］则提出了基于星座点统计特性和OFDM系统等效标量模型的盲估计方法，但该方法需要进行信道估计和均衡，且所要求的先验知识较多。文献［6］在文献［5］基础上，提出利用矢量图最小环带模值方差，对OFDM 雷达信号子载波调制方式进行了识别，但该方法对十六进制正交振幅调制（16QAM）的识别率较低。文献［7-10］提出基于累积量的OFDM 信号子载波调制方式识别方法，但这些方法均需要计算八阶以上的累积量，计算复杂度较高，且对较高阶的正交振幅调制方式识别率不高。

针对上述问题，本文提出一种新颖的OFDM 雷达信号子载波调制方式识别方法，主要以当前较为常见的多进制正交振幅调制（MQAM）和多进制相位调制（MPSK）这两类调试方式开展研究。

1 OFDM 雷达信号模型

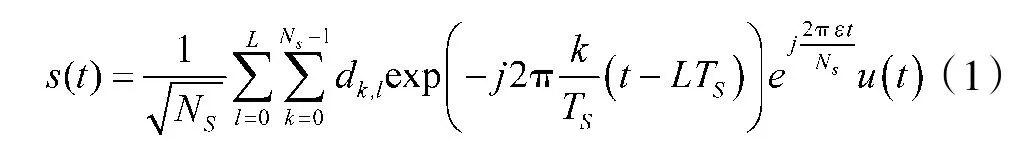
OFDM 发射信号可以表示为：其中，T为OFDM 的符号周期，N为子载波数，L 是发射的OFDM 符号数，ε 为归一化的频率偏移，u（t）表示在［0，T）内的升余弦滤波器，d表示调制在第k 个子载波上第l 个OFDM 符号的数据。假设发射信号通过有M 条路径的多径信道，第m 条路径的信道响应函数为h（m），则接收端接收的信号为：

2 OFDM 雷达信号子载波调制方式识别方法

2.1 MQAM 与MPSK 类间识别

OFDM 雷达信号子载波的调制方式主要有MQAM 和MPSK 两种。其中，相位调制（MPSK）信号在调制信息时只有相位发生跳变，而瞬时幅度变化较小，因此，其瞬时幅度平均值趋于恒定，而正交振幅调制（MQAM）信号存在幅度调制，其瞬时幅度是波动的，据此提出基于幅度瞬时特征的子载波调制方式识别方法，通过提取OFDM 雷达信号瞬时幅度绝对值标准偏差，实现OFDM 雷达信号子载波MQAM 和MPSK 两大类调制方式的类间识别。瞬时幅度绝对值标准偏差定义为：

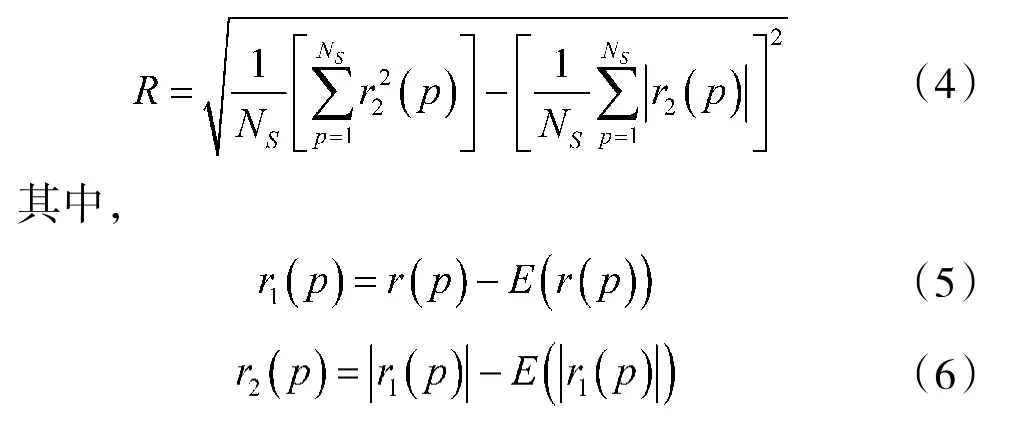
r（p）为接收到的第p 个样本的瞬时幅度。

由多进制相位调制特点可知，不同阶数的相位调制信号的瞬时幅度绝对值标准偏差趋于恒定，因此，其瞬时幅度绝对值标准偏差R 理论值较小，且其不同阶数的瞬时幅度绝对值标准偏差R 均近似相同，而正交振幅调制存在幅度调制，其幅度是波动的，因此，其瞬时幅度绝对值标准偏差R 理论值较大。又由于不同阶数的MQAM 信号幅度变化个数各不相同，阶数越高，变化幅度越剧烈，其相应的瞬时幅度绝对值标准偏差R 越大。由此可知，可以根据两类调制方式瞬时幅度绝对值标准偏差理论值的差异，实现MQAM 和MPSK 两大类子载波调制方式的类间识别。

2.2 MPSK 子类间的识别

针对MPSK 子类间的识别问题，本文吸取现有OFDM 雷达信号子载波调制方式识别方法的优点，结合单载波调制识别方法中的分级分类思想，提出了一种利用组合高阶累积量对MPSK 的调制阶数进行识别的方法，首先给出高阶累积量的定义：

对于一个具有零均值的平稳复随机过程s（k），它的p+q 阶累积量可以写为：

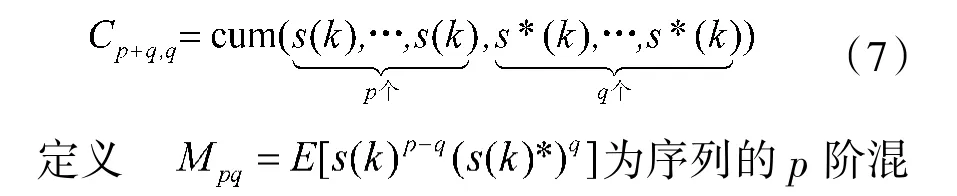
由于OFDM 雷达信号是由多路相互正交的子信号复合而成，每个子信道带宽较窄，可以看成是平坦衰落的，因此，OFDM 雷达信号可以看作是一个均值为零的平稳复随机过程。现考虑将OFDM 雷达信号不同累积量的组合作为子载波调制方式的分类特征量，则对于OFDM 雷达信号，其子载波调制方式的分类特征量定义为：

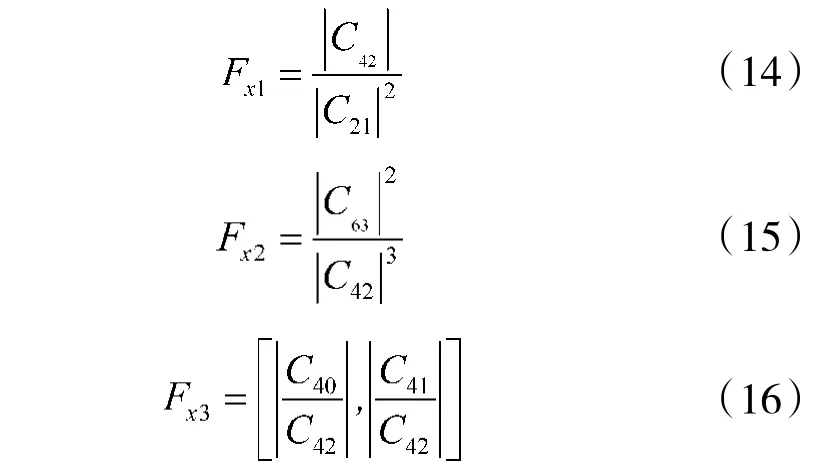
通过计算得出理想情况下各阶MPSK 分类特征量的理论值如表1 所示。

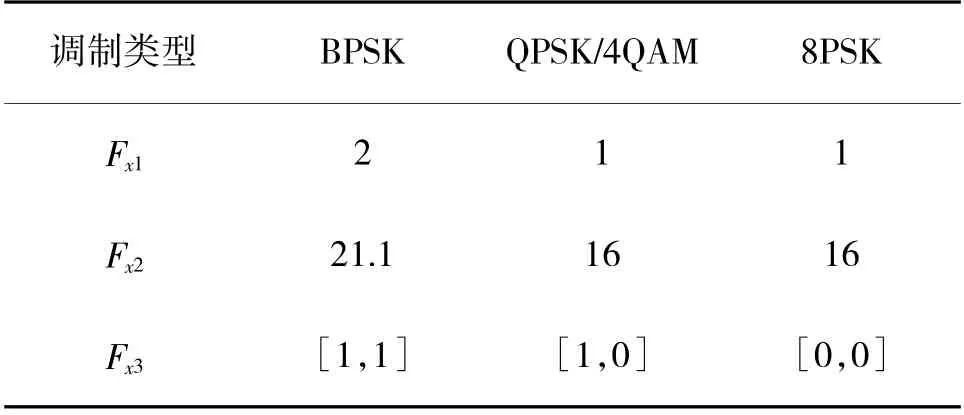
表1 不同阶的MPSK 分类特征量理论值

通过计算实际接收信号各类特征量的数值，结合表1 中的理想值，以F、F、F的顺序依次判决分类，F、F、F的3 种不同取值分别对应识别子载波调制方式为2PSK、QPSK、8PSK，利用这3 种分类特征量理论值的差异，最终实现不同阶MPSK 的识别。

2.3 MQAM 子类间的识别

利用2.2 节中的子载波调制方式识别方法，对MQAM 的子载波调制方式进行识别。通过计算得出理想情况下各阶MQAM 分类特征量的理论值，如表2 所示。

由表2 可知，对于较高阶的MQAM（M＞16）调制方式，由于所得高阶累积量数值上较为接近，难以设置门限进行区分，因此，采用递归降价的方法，实现较高阶MQAM 调制方式的识别。具体过程如下：

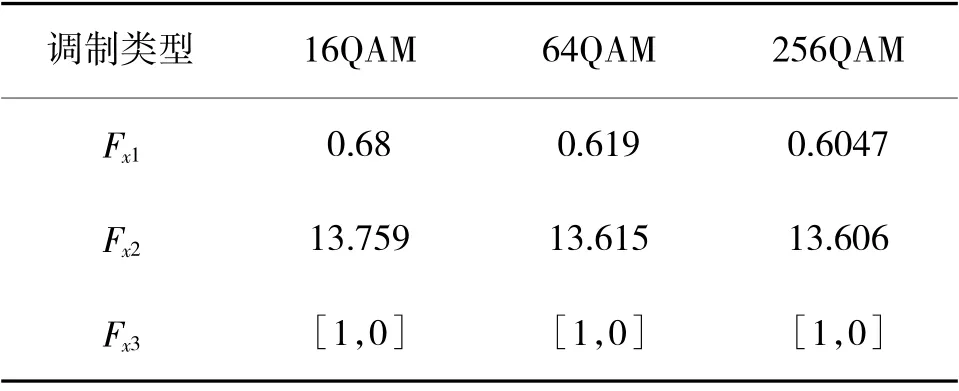
表2 不同阶的MQAM 分类特征量理论值

结合式（3），将接收到的MQAM 信号简化为：

将上式以接收信号的实虚部形式可以表示为：

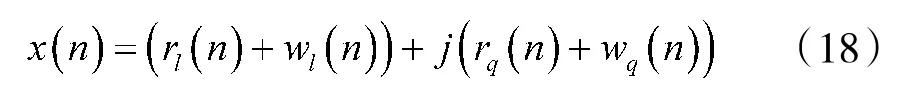
执行一次降价操作，得到新的信号序列为：

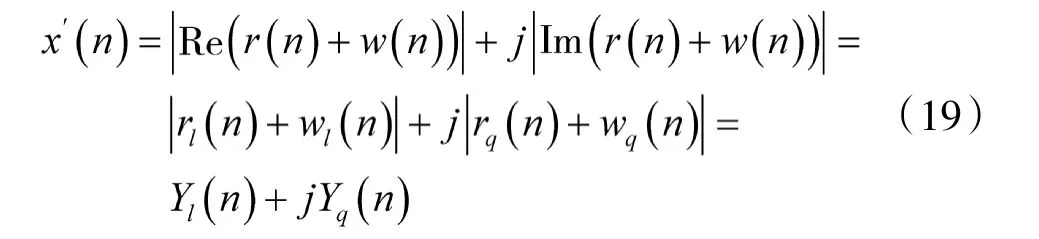
由接收信号性质可知，Y（n）的概率密度函数（PDF）可以表示为：

2.4 调制方式识别流程

图1 为本文方法识别OFDM 雷达信号子载波调制方式的流程图，基本步骤归纳如下：

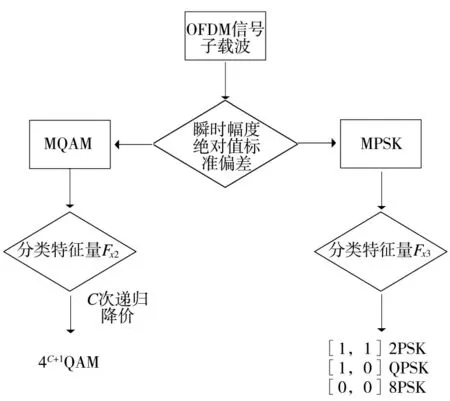
图1 OFDM 雷达信号子载波调制方式识别流程图

步骤1 结合式（4），计算接收到的OFDM 雷达信号瞬时幅度绝对值标准偏差，通过比较其数值大小，对MQAM 和MPSK 两类调制方式进行识别。

步骤2 若接收信号判决为MPSK 调制信号，则利用式（16）计算出信号的分类特征量F，根据不同阶数的相位调制方式对应的分类特征量，实现相位调制方式的阶数识别。

步骤3 若接收信号判决为MQAM 调制信号，则结合式（15），计算信号的分类特征量F，并利用递归降价的方法对MQAM 的阶数进行识别。

步骤4 结合前3 步的识别结果，对OFDM 的子载波调制方式进行判决，得出具体的调制方式类型及对应的调制阶数。

3 仿真实验与分析

为了验证算法的性能，通过Matlab 仿真平台对本文提出的OFDM 雷达信号子载波调制方式识别方法进行仿真实验，仿真条件设置为：OFDM 雷达信号的符号数为200，子载波数为512，符号周期长度是0.8 ms，成型脉冲为矩形，子载波调制方式为16QAM，循环前缀长度占有效符号长度的1/4，过采样率为4。信道环境设置为6 条路径的多径信道，多径时延分别为［0，15，20，30，50，100］ns，平均衰减功率分别为［0，-1，-9，-10，-15，-20］dB，信噪比变化范围为0～30 dB，步进为2 dB。

3.1 MQAM 与MPSK 类间的识别结果

在本节实验中，为验证本文算法对MQAM 和MPSK 进行类间识别的有效性，在不同信噪比条件下，仿真出不同阶数的MQAM 和MPSK 信号的瞬时幅度绝对值标准偏差及对应的正确识别率，并与文献［4］中的方法进行性能对比。仿真实验结果如图2所示。

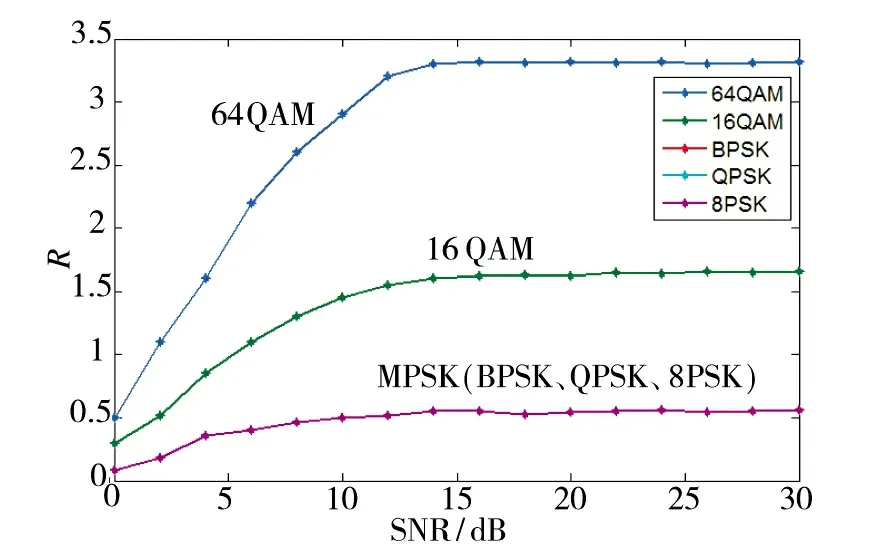
图2 瞬时幅度绝对值标准偏差随信噪比分布

图2 为不同子载波调制方式的瞬时幅度绝对值标准偏差随信噪比的分布，由图2 可知，两类调制方式的瞬时幅度绝对值标准偏差，随信噪比的提高而增大，相位调制（MPSK）的瞬时幅度绝对值标准偏差数值较小且不同阶数的瞬时幅度绝对值标准偏差数值相同，这是由于不同阶数的相位调制信号在调制信息时，只产生相位的跳变，其瞬时幅度基本保持不变，因此，不同阶数的瞬时幅度绝对值标准偏差数值相同。而对于正交振幅调制（MQAM），其瞬时幅度绝对值标准偏差数值较大，且调制阶数越高，其瞬时幅度绝对值标准偏差越大，这是由于正交振幅调制存在幅度调制，其幅度数波动的，且调制阶数越高，波动越剧烈，因此，瞬时幅度绝对值标准偏差大于相位调制，符合理论分析结果。当信噪比大于3 dB 时，MQAM 与MPSK 的瞬时幅度绝对值标准偏差存在较明显的差异，此时可以将两类信号进行较好的分类。

图3 给出了本文方法对MQAM 和MPSK 类间识别的正确识别率，由图可知，两种方法的正确识别率均随信噪比的提高而上升，当信噪比达到5 dB时，本文方法的正确识别率可达到100%，而此时文献［4］方法的正确识别率仍达不到50%。当信噪比提升至12 dB 时，文献［4］方法的正确识别率才可达到100%。而在信噪比小于10 dB 时，本文方法的正确识别率明显高于文献［4］的方法，因此，本文方法相比文献［4］的方法对信噪比要求更低，相同信噪比条件下识别性能更优。

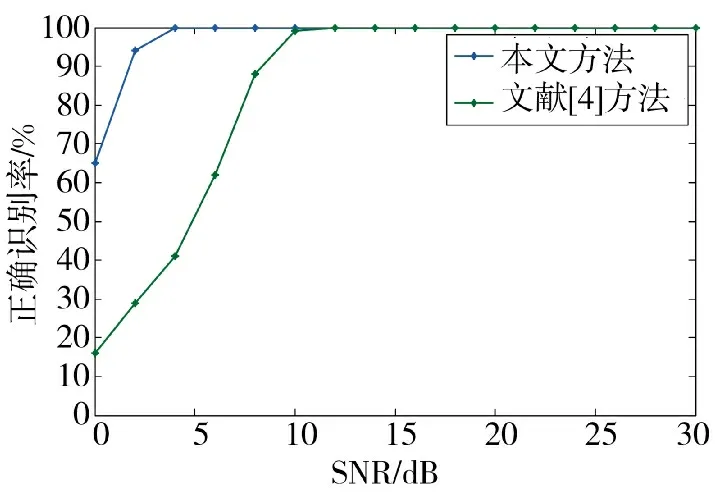
图3 MQAM 和MPSK 的类间正确识别率

3.2 MPSK 子类间的识别结果

在本节设置的实验条件下，对本文提出的MPSK 调制方式子类间的识别方法进行正确识别率仿真，并与文献［4］中的方法进行对比，实验结果如图4 所示。

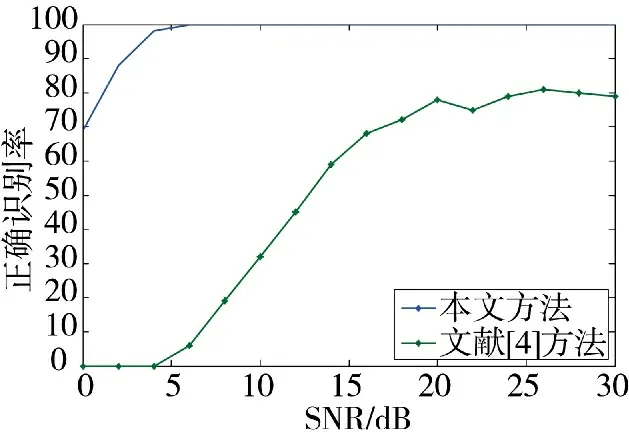
图4 MPSK 的平均识别率

由图4 可知，本文方法的识别性能明显优于文献［4］的方法，两种方法的正确识别率均随信噪比的提高而均匀上升，在信噪比为6 dB 时，本文方法的正确识别率即可达到100%，可以实现MPSK 子类间调制方式的识别，而此时文献［4］方法的正确识别率还不到10%，无法正确估计出OFDM 雷达信号子载波的调制方式。当信噪比提高至30 dB 时，文献［4］方法的正确识别率仍低于80%，无法完全正确识别出OFDM 雷达信号子载波的调制方式。由此可见，本文方法与文献［4］方法识别MPSK 子类间调制方式要求的信噪比条件是不同的，在相同信噪比条件下，本文方法的正确识别率明显高于文献［4］的方法，具有更强的抗噪能力和更优的识别性能。

3.3 MQAM 子类间的识别结果

图5 为本文方法对子载波调制方式为4QAM，16QAM，64QAM，256QAM 的平均正确识别率，并在相同实验条件下仿真出文献［4］方法识别4QAM，16QAM 调制方式的平均正确识别率并进行性能对比。

由图5 可知，本文方法的正确识别率曲线的变化趋势与文献［4］大体相当，在各个信噪比点上的正确识别率相差不大，二者的正确识别率在信噪比达到时接近100 %，对信噪比的要求均比较高，文献［4］方法在部分信噪比点上的正确识别率甚至高于本文方法。但针对正交振幅调制方式的识别，文献［4］方法只能识别4QAM，16QAM 的调制方式，无法对更高阶的MQAM 调制方式进行识别，而本文方法不仅可以识别4QAM，16QAM 的调制方式，更能识别64QAM，256QAM 等更高阶的子载波调制方式，识别的子载波调制方式类型更加完备。

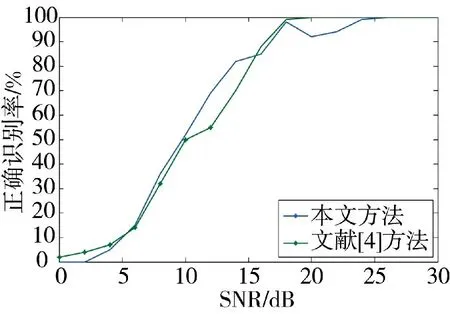
图5 MQAM 的平均识别率

4 结论

本文提出一种新颖的OFDM 雷达信号子载波调制方式识别方法。通过对MQAM 和MPSK 两类调制方式OFDM 雷达信号瞬时幅度的理论分析和比较，得出可以利用瞬时幅度绝对值标准偏差对MQAM 和MPSK 两类调制方式进行类间识别，进而将组合高阶累积量作为识别特征量对MQAM 和MPSK 两类调制方式中的子类进行分级识别，并利用递归降价的方法实现子载波调制阶数M＞16 的MQAM 调制方式的识别。仿真实验结果表明，该方法能够有效实现多径信道下OFDM 雷达信号多种子载波调制方式的识别，且识别性能更优，可以识别更完备的子载波调制方式类型。