基于改进的重心插值提高脉冲雷达测距精度的研究*
马 兰,李照照,扈月松,井 伟,杨雪林
(1.西安电子工程研究所,西安 710100;2.中国兵器工业试验测试研究院,陕西 渭南 714200)
0 引言
测量目标的距离是雷达的基本任务之一。根据雷达发射信号的不同,目标距离的测量可以采用脉冲法、频率法和相位法。本文的研究主要针对脉冲法测距。脉冲法测距的一般方法是根据对目标回波作脉压处理得到的功率谱曲线,找到曲线最大值点对应的距离单元号来计算目标距离。然而,受到采样率的约束,回波脉压结果通常是由一系列离散的采样点构成,在脉压结果主瓣内采样得到的最大值点与回波峰值点之间存在一定的偏差,因此,会带来不可避免的距离量化误差,降低雷达测距精度,所以研究减小距离量化误差的方法是研究雷达测距技术的一项重要内容。
文献[1]先用FFT 得到差频信号极大值和次大值的谱线位置,再根据谱峰极大值估计方法计算出真实极大值的谱线位置,从而实现测距系统的高精度估计,但是该方法计算量较大。文献[2]研究了激光雷达的峰值范围估计和测距精度,通过引入Cramer-Rao 下限,结合仿真实验分析了峰值位置误差随噪声的变化情况,以及脉冲宽度对雷达测距精度的影响,表明Cramer-Rao 下界给出了无偏估计下估计参数的上限。同时,在不同已知参数条件下,得出了雷达距离跟踪精度的变化规律,对研究提高雷达测距精度具有一定的参考价值。文献[3]提出了一种基于抛物线拟合估计回波峰值位置的方法,通过利用距离谱上的最大值点及其左右最近的一个点进行抛物线拟合,使拟合抛物线的中心线接近真实的目标位置。但该方法的缺陷是没有考虑噪声对脉压结果的影响。文献[4]介绍了一种通过对回波主瓣面积作梯形近似来插值估计出真实峰值的方法。首先从回波波形的特点入手,对回波信号中的目标区域进行细化,在固定的采样间隔之间仅作一次插值处理,等效于降低目标回波区域内的采样间隔,在雷达各参数都固定的情况下有效提高测量精度。但采用这种方法时测距精度会明显受到噪声的影响,在有噪声时测量误差会急剧增加。文献[5]介绍的是将包络插值相移相干累积算法在雷达空间碎片的检测中应用,通过从回波能量中提取相关信息,实现了包络插值,达到了提高雷达检测能力的目的。
传统重心插值法是直接利用回波脉压结果主瓣内最大值和次大值采样点的幅度信息和位置信息作重心插值处理,得到回波峰值位置的估计值。实验结果表明,该方法存在较大的固有误差。本文结合先验信息,在时宽、带宽和窗函数确定且不加噪声的情况下,通过在较高采样率下作仿真分析,得到脉压结果主瓣内采样最大值和次大值点的幅值比与脉压波形峰值时间的一一对应关系,利用这一对应关系,对实际采样率下且有噪声存在的脉压结果主瓣内采样最大值和次大值点作重心插值处理,从而实现对脉压波形实际峰值时间更精确的预估,进一步减小了距离量化误差,提高了雷达测距精度。
1 雷达测距量化误差的产生
在雷达测距过程中,影响距离跟踪精度的因素主要包括以下几个方面:接收机热噪声、多路径、目标闪烁、定时脉冲抖动、大气传播误差以及距离量化误差。本文主要针对减小距离量化误差来提高雷达测距精度。
雷达测距的一般公式为:

式中,c 为电磁波传播速度(在自由空间传播时约等于光速),t为电波在雷达站与目标之间往返一次所需的时间。
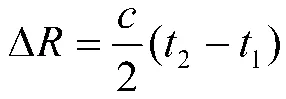
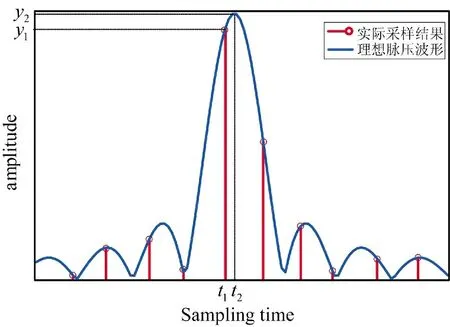
图1 雷达测距量化误差的产生
本文提出了一种基于重心插值来预估峰值时间的插值方法。结合先验信息,当雷达发射信号为LFM 信号,时宽、带宽和窗函数确定且不加噪声的情况下,回波峰值位置与脉压结果主瓣内的采样最大值和次大值点的幅值比之间存在一一对应的关系。将噪声下脉压结果主瓣内得到的采样最大值和次大值点的幅值比,与先验信息下的幅值比进行比较,找到最接近此时幅值比的回波峰值位置关系,再根据采样最大值和次大值点对应的采样时间作重心插值计算,便可更精确地估计出回波峰值时间,减小距离量化误差,提高雷达测距精度。
2 重心插值算法的基本原理
2.1 重心插值算法

将上述定义的质点系应用到雷达回波脉压结果的主瓣波形中。结合先验信息可知,雷达回波脉压结果的主瓣波形可近似为一高斯分布曲线,而回波峰值出现的位置就是该高斯分布曲线的均值。直观理解,均值就是一个随机变量所有可能取值的加权平均值,权就是这些可能取值相应的概率。
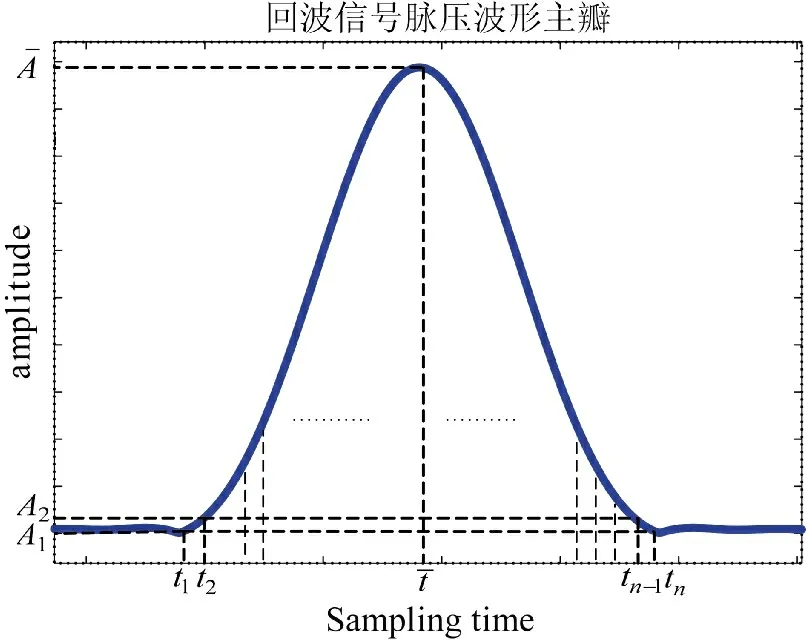
图2 回波信号脉压波形主瓣采样点分析


2.2 回波峰值位置与采样点位置、采样点幅值比之间的关系推导
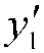
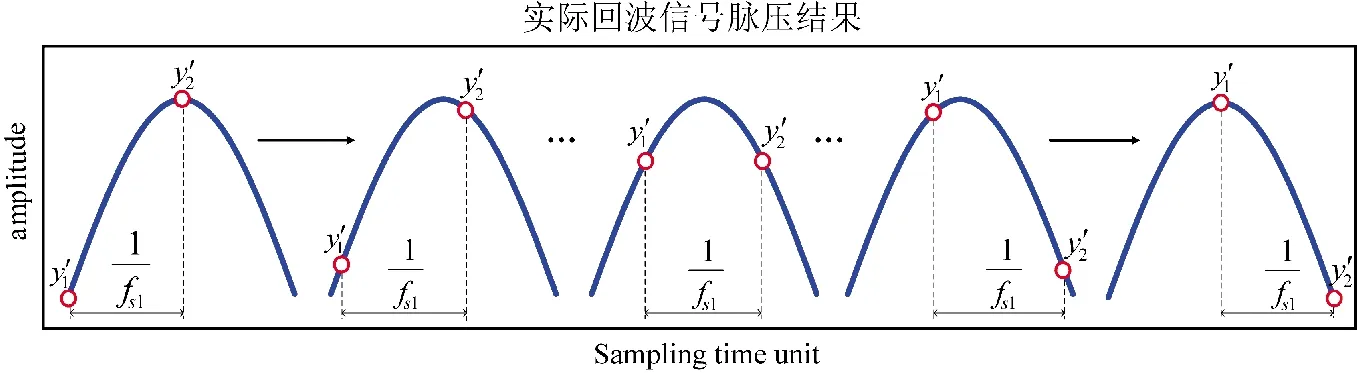
图3 实际回波信号脉压结果中最大值和次大值的幅值关系分析
2.2.1 回波峰值位置与采样点位置的关系推导
实际工程中,雷达回波信号脉压结果3 dB 波束宽度内一般只有两个采样点,且这两个采样点的SNR 较高,故期望通过这两个采样点的幅值信息和位置信息来作插值处理估计出回波峰值位置。
假设这两个采样点按时序的幅值分别为y和y,对应的采样时间单元分别为t和t,采样时间单元就是采样时间与采样率f的乘积。将回波峰值处的采样时间单元表示为t,则根据式(4)假设下式成立:
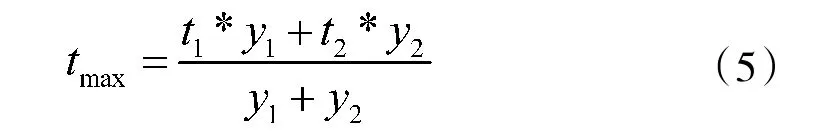
实际中,即使回波中没有噪声,直接用这两个采样点的信息作插值处理也无法得到精确的t值,存在一定的固有误差。原因分析如下:
当式(5)成立时有:
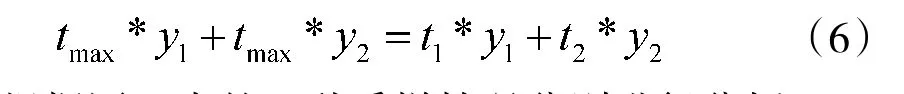
根据图3 中的5 种采样情况分别进行分析:
第1 类情况下,采样最大值点就是脉压波形的峰值,此时t=t,显然式(6)不成立。要使其成立,需使y趋于0;
第2 类和第4 类情况下,采样最大值和次大值点分别位于脉压波形峰值位置的两边,即t<t,t>t,且两个采样点幅值相差较大,此时直接用式(5)作插值处理估计峰值位置时,产生的固有误差为:
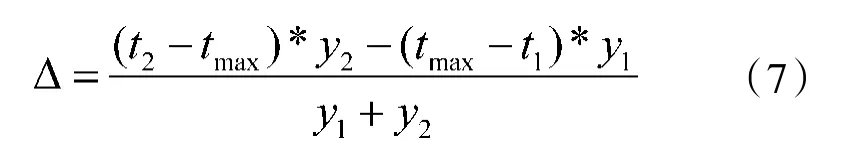
且该误差不会随SNR 的增大而减小;
第3 类情况下,脉压结果采样最大值和次大值点幅度基本相同,波形峰值位置恰好在这两个采样点的中心,此时式(6)成立,可直接用式(5)插值估计波形峰值位置,且精度较高;
第5 类情况与第1 类相似,此时t=t,要使式(6)成立,则应使y趋于0。
为解决上述问题,本文提出以下方法。

结合图3 可知,在回波脉压波形的主瓣内,无论真实的峰值时间单元t位置如何变化,t与最大值和次大值点对应的采样时间单元t、t的位置关系均可以被仿真出来,且这种位置关系与雷达其他参数的设计无关。以下对这一关系作仿真验证。
雷达参数设计如表1 所示。在回波脉压结果主瓣波形内选择两个采样间隔对应的波形进行仿真分析,如图4 所示。

表1 雷达仿真参数设计1
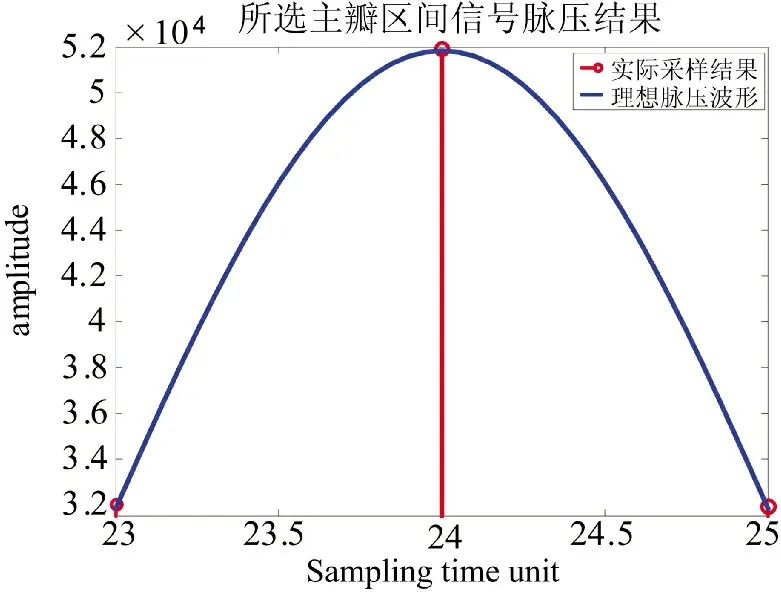
图4 回波脉压结果所选主瓣波形
此时参考频率f下回波峰值位置对应的采样时间单元t′为24,将采样最大值和次大值点在所选主瓣波形上进行移动,使峰值位置t′与最大值和次大值点对应的采样时间单元t′、t′的位置关系均被考虑到,如图5 所示。
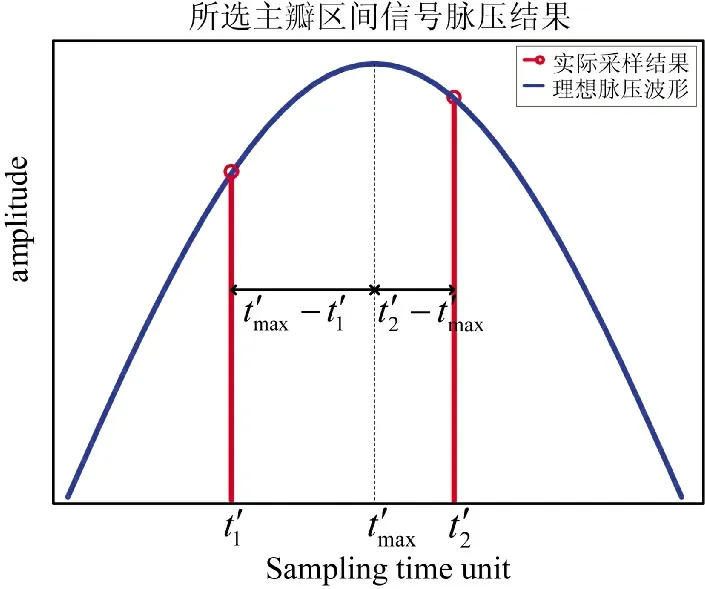
图5 采样点位置与峰值位置关系的一种情况分析
将图5 中t′和t′分别在采样时间单元[23,24]和[24,25]之间移动,则结合参考频率f可知,采样点位置仿真共有41 种情况。结合式(9)计算出各种情况下使式(8)成立的理想幅值比K,数据统计如表2 所示。

表2 信号脉压结果峰值位置与采样点位置关系分析1
改变雷达参数设计如表3。

表3 雷达仿真参数设计2
经过仿真分析,该组参数下回波峰值位置对应的采样时间单元t′为47,故选择将t′和t′分别在采样时间单元[46,47]和[47,48]之间移动,结合式(9)得到此时的理想幅值比K 值如表4。
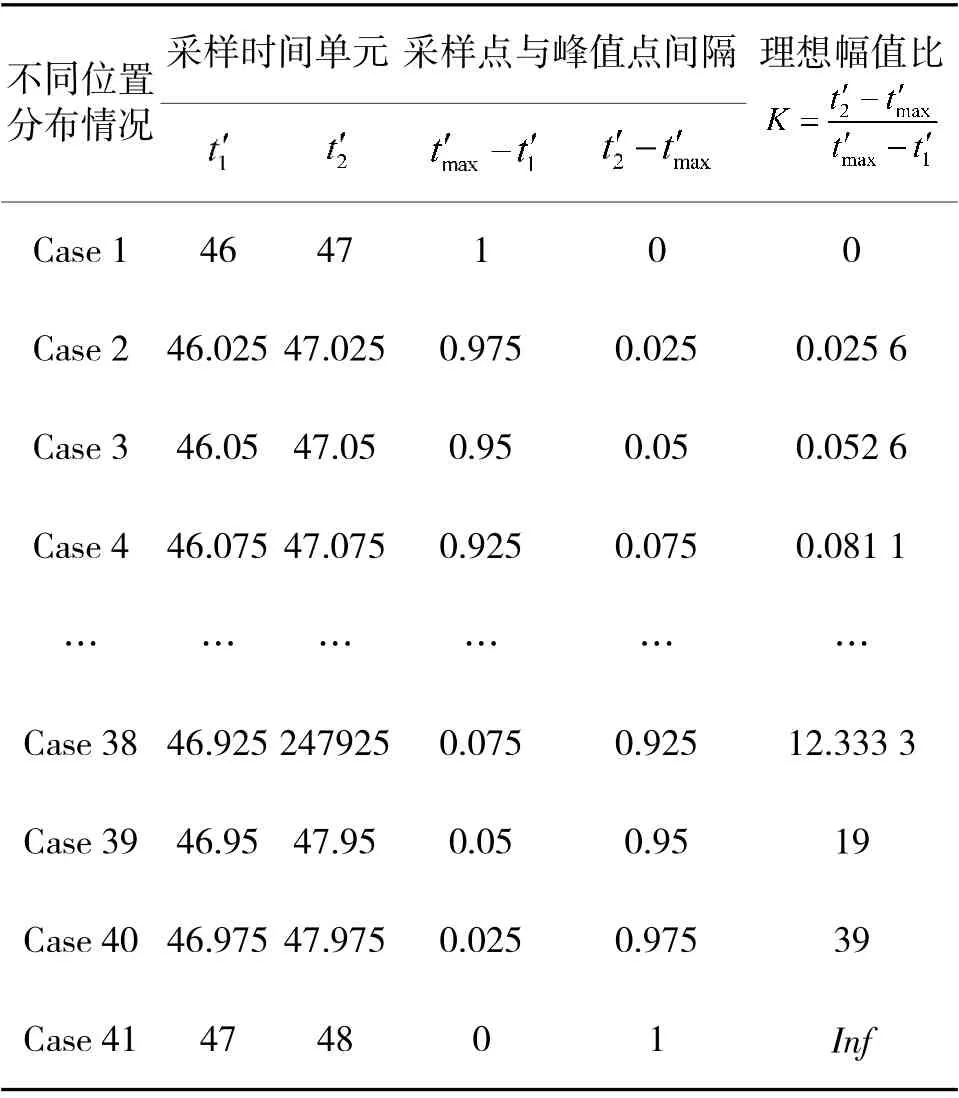
表4 信号脉压结果峰值位置与采样点位置关系分析2
参见表2 和表4 的仿真数据可知,任何雷达参数设计下,回波峰值位置与已知采样最大值和次大值点的位置之间的各种关系均可被仿真得到,且参考频率选的越大,仿真的情况越多,越有利于后面的计算。
2.2.2 回波峰值位置与采样点幅值比的关系推导
以下仿真均是在表1 中的雷达参数设计下进行。首先在未加噪声和加噪声的情况下分别对图3中回波信号脉压结果的最大值和次大值的幅值比Q=y′/y′进行对比分析。
结合图6 仿真结果可以看出,在不同snr 下,同一采样位置对应的采样点幅值比Q 基本相同,且随着snr 的增大,同一位置处的幅值比与未加噪声时的幅值比越来越接近。
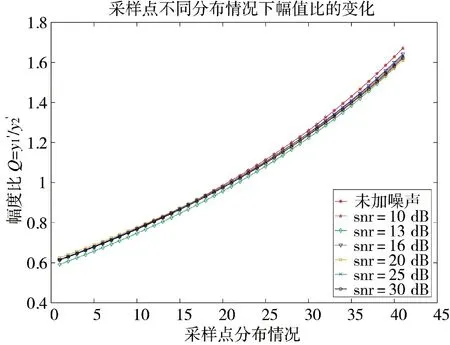
图6 不同snr 下各采样位置对应的采样点幅值比分析
根据以上结论,以未加噪声时各采样点位置分布情况下的Q 值作为基准,在该Q 值与表2 中的理想幅值比K 值之间建立一一对应的关系,如表5所示。
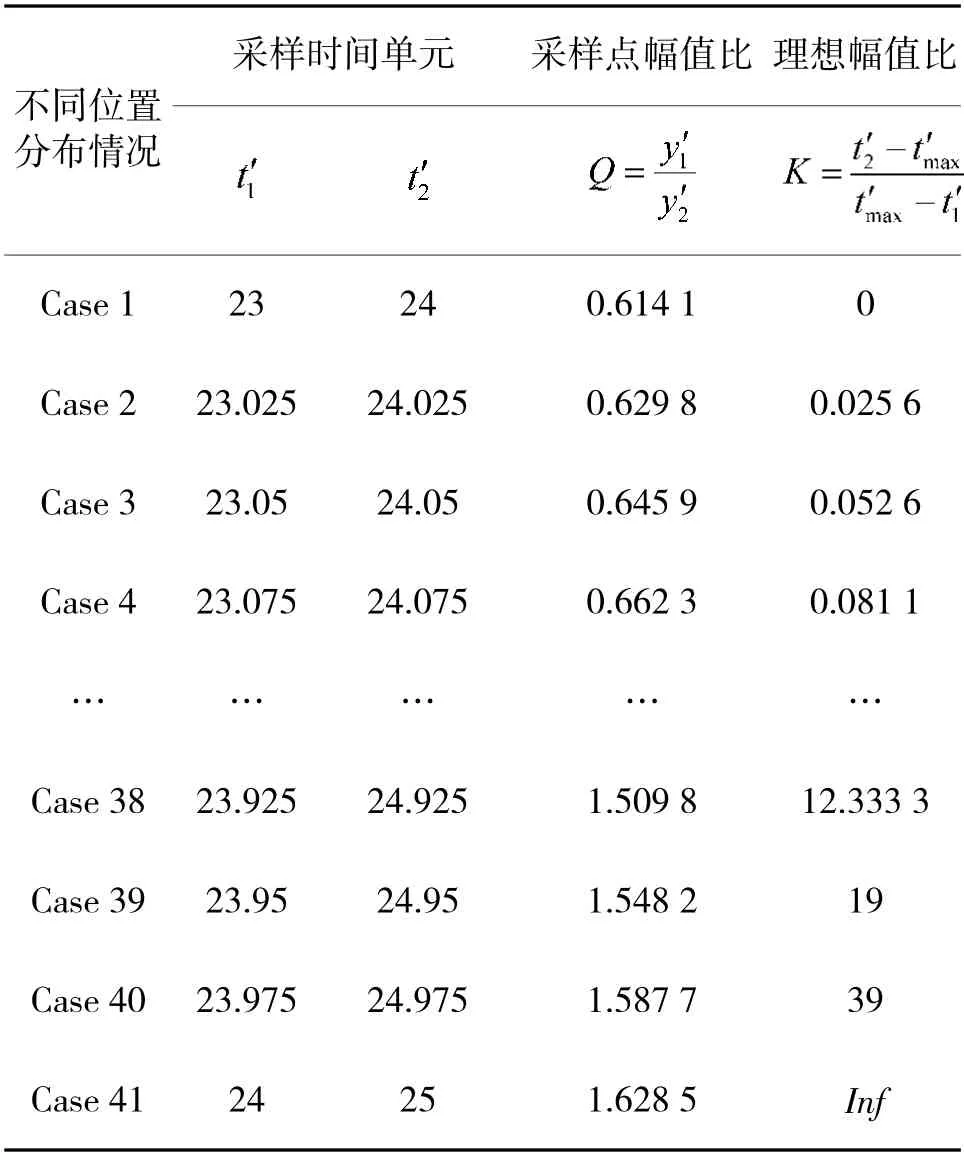
表5 采样点幅值比与理想幅值比之间关系分析
由以上仿真分析可知,当雷达参数设计给定时,首先可以在不加噪声的情况下选择较高的采样率仿真,得到近似连续的回波脉压波形。在近似连续的回波脉压波形主瓣内以实际采样率确定采样间隔,依次取两个采样点,使采样点遍布脉压波形的主瓣。按时序依次将这两个采样点对应的采样时间单元t′、t′和幅值比Q=y′/y′记录下来。以较高采样率下近似连续的回波脉压波形峰值时间单元作为t′值,结合采样时间单元t′、t′便可根据式(9)依次计算出理想幅值比K 值。此时Q 值和K 值一一对应。
最后,对实际采样率下有噪声存在的回波脉压结果中采样最大值和次大值点,按时序计算出此时的幅值比Q=y/y。由图6 可知,Q′与此时的Q 值之间误差很小。将Q′与Q 进行对比,找到最接近Q′的Q 值,也就找到了此时的理想幅值比K 值。将该K 值代入式(7),便可插值估计出回波峰值所在的采样时间单元t,再除以实际采样率就是回波峰值时间。
3 仿真实验
图7 表示本文所提出的估计回波脉压峰值时间的方法流程图。结合表1 中的雷达仿真参数设计,加入噪声进行仿真验证,分析经过该方法插值处理后距离量化误差的变化。将snr 的取值设置为10 dB~30 dB,即共有21 个snr 值。
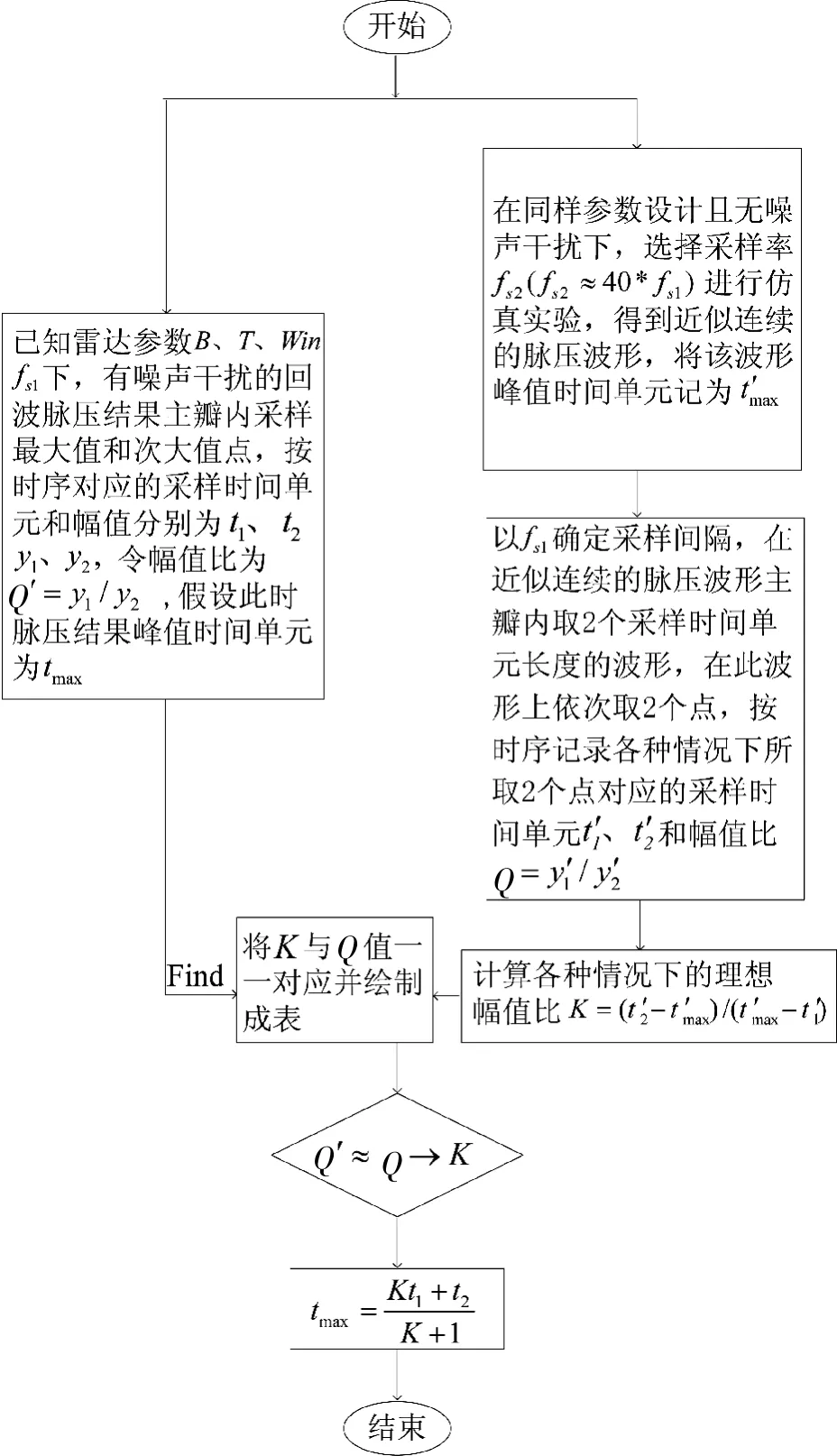
图7 改进的重心插值法估计回波脉压峰值时间流程图
由于表1 中实际采样率f=2.5 MHz,即回波脉压结果采样点间隔为0.4 us,故选择以下4 种采样最大值和相邻次大值点位置分布情况进行仿真分析。
针对以上4 种采样最大值和相邻次大值点位置分布与回波峰值位置t的关系,当snr 从10 dB~30 dB 变化时,用本文提出的方法对已知采样点作插值处理来估计回波峰值出现的采样时间t,最后计算出距离量化误差,并与传统重心法进行比较。
根据仿真结果可以看出,传统重心法在大多数情况下都存在一定的固有误差,即当snr 增加到某个值时,距离量化误差不再随snr 的增加而减小。图8(a)中所示情况下产生的固有误差最大,约为25.5 m,此时无论snr 如何增加,该误差几乎不变,原因是此时次大值点偏离峰值点位置较远,信噪比较小,对采样点幅值影响较大。而图8(c)中采样最大值与相邻次大值点信噪比分布相对均衡,幅值相差很小,用传统重心法插值处理后估计的回波峰值位置接近两个采样点的中心位置,所以最终带来的固有误差最小。而本文提出的改进后的重心插值法不仅在snr 较小时产生的测距误差明显减小,最大误差仅有12 m,且随着snr 的增大,雷达测距误差收敛,逐渐减小至0.2 m。原因是随着snr 的增大,采样点幅值比Q′值越来越接近对应的Q 值,对回波峰值位置的插值估计越来越精确。
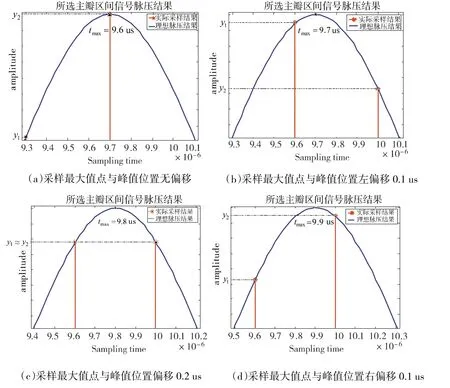
图8 采样最大值点与回波峰值位置的不同偏移情况分析
其中,值得注意的是,在图9(c)所示的情况下,无噪声干扰时两个采样点幅值比Q′=1,回波峰值位置恰好处于两个采样点的中心,但由于实际中噪声是随机存在的,故Q′值会在1 附近波动,且经过仿真实验发现,当snr 从10 dB~30 dB 变化时,该采样位置下Q′值的波动范围在0.957 2~1.063 2 之间。此时,用该方法估计回波峰值位置时,可直接用Q′=1对应的理想幅值比K=1 进行插值处理,减小噪声对Q′带来的误差,进一步提高测距精度。
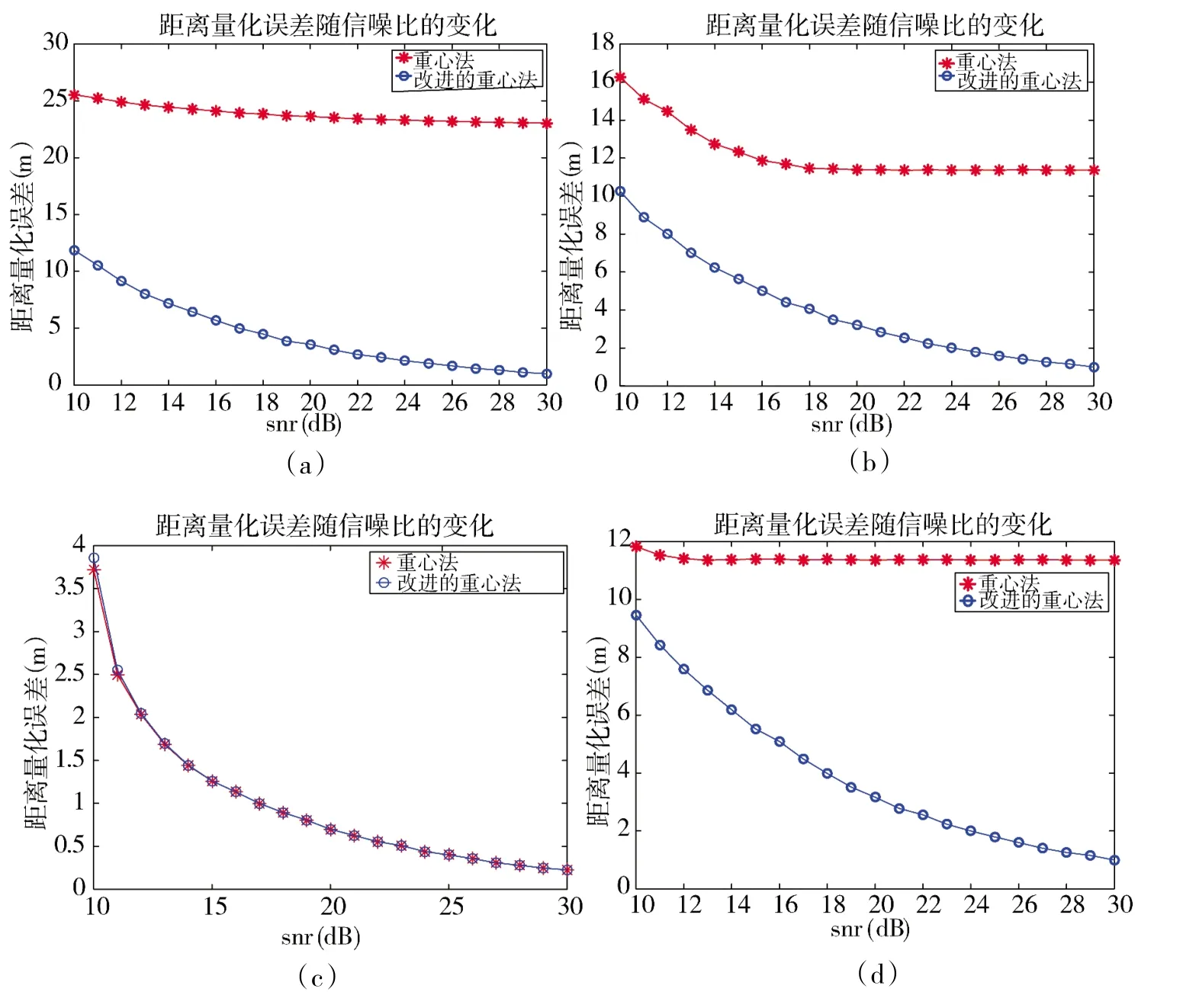
图9 采样点与回波峰值位置不同偏移情况下距离量化误差随的变化
4 结论
本文针对脉冲法雷达测距中距离量化误差的存在,提出了一种基于重心插值提高雷达测距精度的方法。该方法是结合先验信息,选择较高采样率将回波脉压波形峰值时间与各种采样最大值和次大值点分布情况下的位置关系仿真出来,同时在采样最大值和次大值的幅值比,与该位置关系之间建立一一对应的联系。最后将实际工程中噪声下得到的采样点幅值比与仿真中的数据进行对比,找到未加噪声下最接近该情况的采样点幅值比,根据此时峰值时间与两个采样点的位置关系,便可插值估计出回波峰值时间。实验结果表明,与传统的重心插值算法相比,该方法可以明显减小传统方法产生的固有误差,使插值处理后的脉冲雷达测距误差随snr 的增加逐渐收敛,实现了对包络峰值位置更精确的估计。

