基于改进方差最大化的主客观组合赋权方法

李晓菲，缪建明，沈丙振

（中国兵器工业信息中心，北京 100089）

0 引言

评估指标权重赋值的合理性对武器装备体系评估结果影响巨大，研究人员开展了广泛研究。从国内外相关研究成果总结来看，评估指标权重赋值方法大致可分为3 类，分别是主观赋权法、客观赋权法和主客观组合赋权法。主观赋权法包括层次分析法、二项系数法等，主要是根据专家的经验和知识，通过对各项评估指标进行两两对比，在此基础上检验形成各项评估指标的权重。主观赋权法主要依赖于专家经验，承载了过多的主观随意性，反映的是专家过去的经验积累以及对赋权的一个主观把握，打分难以对权重精确刻画，赋权结果反映权重整体趋势，但难以准确定量描述。客观赋权法包括主成分分析法、熵权法、CRITIC 等，是利用各个指标的客观信息即指标值来确定指标权重的方法。客观赋权法不依赖于专家经验，赋权结果取决于样本数据的科学合理性，结果相对客观，但客观赋权法对样本数据的完备性及样本量有较高的要求，其赋权结果可解释性和稳健性弱于主观赋权法。

近年来，研究人员兼顾主客观赋权法各自优点，将两种赋权方法结合使用，形成了多种组合赋权法，包括加法合成法、乘法合成法等，它们的主要区别是主、客观权重向量的分配系数所采用的方法不同。其中，加法合成法中常用的主要有主客观权重偏差平方和最小赋权法、主客观评价结果差异最小赋权法、方差最大化组合赋权法。乘法合成法一般是先将指标的主客观权重相乘再进行归一化，这导致了主、客观权重大的指标组合权重更大，而权重小的指标组合权重更小，无法解释组合权重的合理性。以上方法虽然都有一定借鉴意义，但在主客观权重的分配上还没有运用合适的方法，对权重组合方式还需进一步研究。本文在方差最大化组合赋权的基础上构造了冲突性参数，用于解决特征之间相关性过强的问题，形成了一种改进方差最大化组合赋权方法，在主客观指标权重排序一致的前提下，综合考虑指标的离散程度和指标之间的相关性来确定组合权重。

主观赋权法过于依赖专家经验，客观赋权法完全由样本数据决定，赋权结果更加客观，但又未考虑专家的经验，有时赋权结果与属性实际重要程度相悖，并且结果难以给出明确解释，由此，组合赋权法应该将指标权重分为排序和赋值两项内容，在考虑排序结果一致的情况下对主观权重进行组合赋权。本文以主观权重的排序为标准，在主、客观权重排序完全一致的情况下，对所有指标采用改进方差最大化组合赋权法计算指标权重；当主、客观权重排序部分一致时，则对部分指标权重进行改进方差最大化组合赋权并归一化；如主、客观权重排序完全不一致，则仍以主观权重作为最终的指标权重。

1 权重计算流程

本文提出的基于主客观权重排序的组合赋权法如图1 所示。在武器装备能力评价指标的权重求解过程中，将指标权重分为指标权重排序和指标权重赋值两项内容，在主观权重的指标排序前提下进行主客观组合赋权。

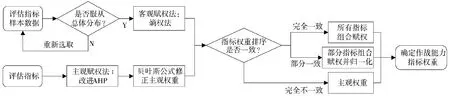
图1 权重求解流程图

具体步骤如下：

1）计算主观权重，并进行排序处理，得到指标、权重数组。主观赋权法为贝叶斯公式修正的改进AHP 法，即通过多位专家进行群决策，利用贝叶斯方法对专家的先验权重加以修正得到的后验权重作为指标的主观权重。

2）计算客观权重并排序处理，得到指标、权重数组。首先，考察计算客观权重的指标数据信息是否服从总体分布，若服从正态分布说明样本数据可以反映总体，计算的客观权重相对合理；否则需要重新选取样本。其次，按照熵权法计算客观权重。最后，形成指标、权重数组。

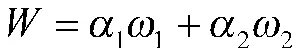
4）基于以上方法确定最终的指标权重。

2 改进方差最大化组合赋权法

在多指标综合评价问题中，指标之间必然会存在一定的相关性，如果指标之间的相关性太强，在综合评价过程中必然会导致信息的重迭，从而影响评价结果的合理性，甚至会歪曲评价对象的排名。

基于方差最大化原则，权重应当使得所有指标对于多个样本的总方差达到最大，可以得到的各个方案评价值比较离散。本文基于方差最大化原理提出一种改进方差最大化组合赋权法，即在方差最大化组合赋权法的基础上考虑指标之间的冲突性，用于衡量指标之间相关性的强弱，使冲突性越大的指标所分配到的权重大些，冲突性越小的指标分配到的权重小些。指标之间的冲突性R，用相关系数r进行表示，若两个指标之间的相关性越强，则冲突性越小，所能体现的评价信息重复性就越强，指标的权重就应越小。

基于改进方差最大化方法，权重向量应当使得所有n 个指标对所有m 个决策方案的改进总方差达到最大。由此可以构建如下线性规划模型：

为了求解上述最优化问题，可以构造拉格朗日函数如下：

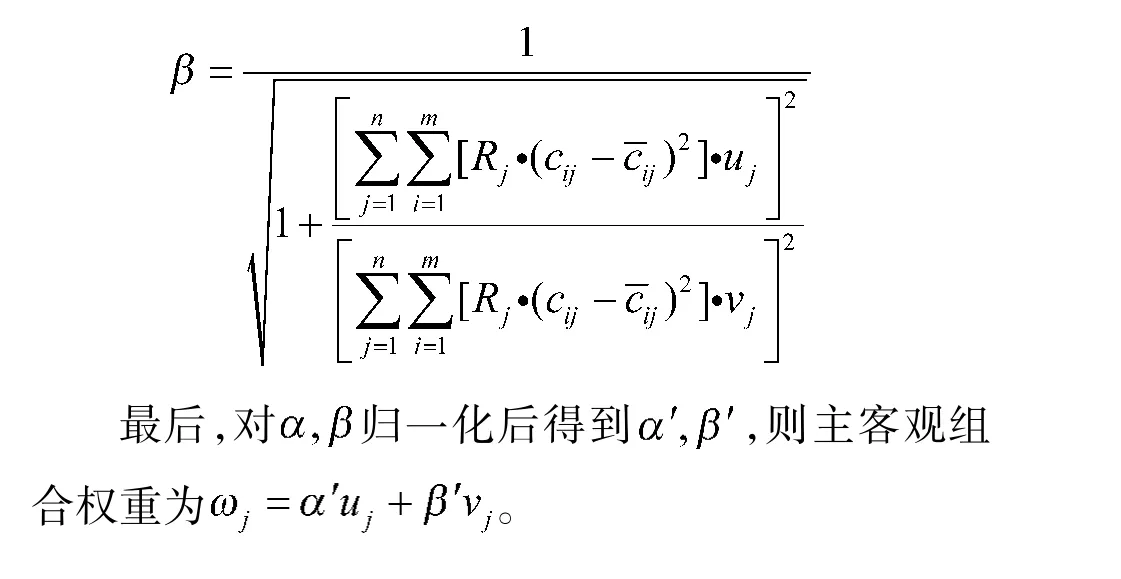
3 实例分析

3.1 装备体系能力评估指标体系的构建

某武器装备体系的装备体系能力指标包括侦察识别率、有效侦察率、通信成功率、计划分发时延、机动速度、野战抢救效率、毁伤率和打击命中率共8 项指标，如图2 所示。

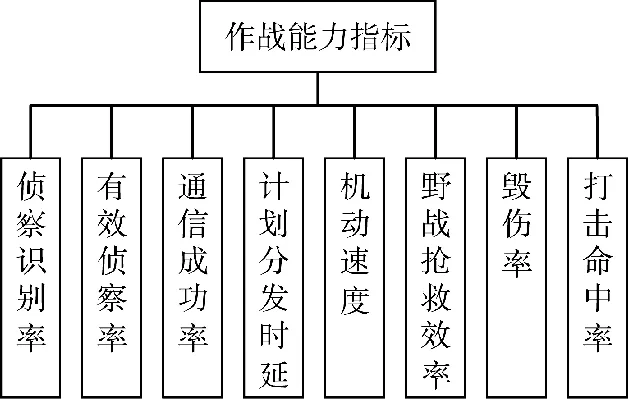
图2 武器装备体系能力指标

3.2 主观权重的计算

经权威专家对上述8 项指标进行两两比较，得到判断矩阵如下所示，判断矩阵中的所有元素表示针对装备体系能力的相对重要性，对角线上的元素均为1，表示各个指标与自身的对比，如第1 行第2列的元素表示侦察识别率的重要程度是有效侦察率的2 倍。

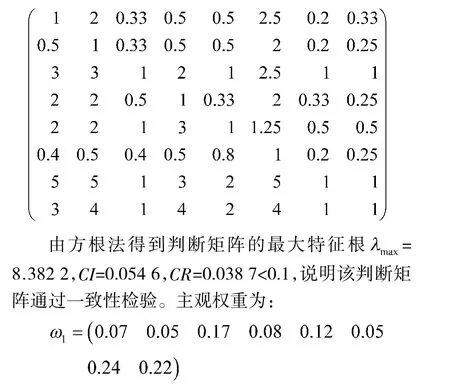
本文选取5 位专家分别将8 项指标两两比较，给出各自的判断矩阵，再确定各位专家的先验权重， 利用贝叶斯权重修正法得到主观权重如表1 所示。

表1 指标主观权重

3.3 客观权重的计算

由于上述8 项指标的总体分布均为正态分布，所以对上述8 项指标的归一化数据进行正态分布检验，运用python 中的shapiro 模块（专门用来做正态性检验的模块）计算得到P 值如表2 所示，当P值＞0.05 时说明服从正态分布。由表2 可知，8 项指标均服从正态分布。

表2 正态分布检验的P 值

图3 是各项指标的归一化数据对应的直方图，可以直观地看到各项指标的样本数据分布趋势均服从正态分布。

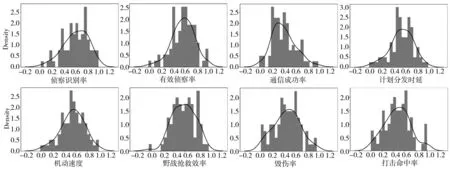
图3 指标样本数据的直方图

由熵权法计算指标熵值及其客观权重的过程如表3 所示，第1 行代表指标的熵值，熵是对不确定性的一种度量，指标的熵值越小，不确定性就越小，信息量就越大，指标的样本数据间的差异就越大，对评价对象的区分能力也越大，相应的权重也越大。

表3 熵权法的计算结果

3.4 组合权重的计算

由主客观两种赋权方法对某武器装备体系的指标进行赋权，结果如下页表4 所示。8 项指标的主、客观权重的排序完全一致，主、客观权重的所有指标排序相同，为毁伤率＞打击命中率＞通信成功率＞机动速度＞计划分发时延＞侦察识别率＞有效侦察率＞野战抢救效率，所以对所有指标进行权重组合。

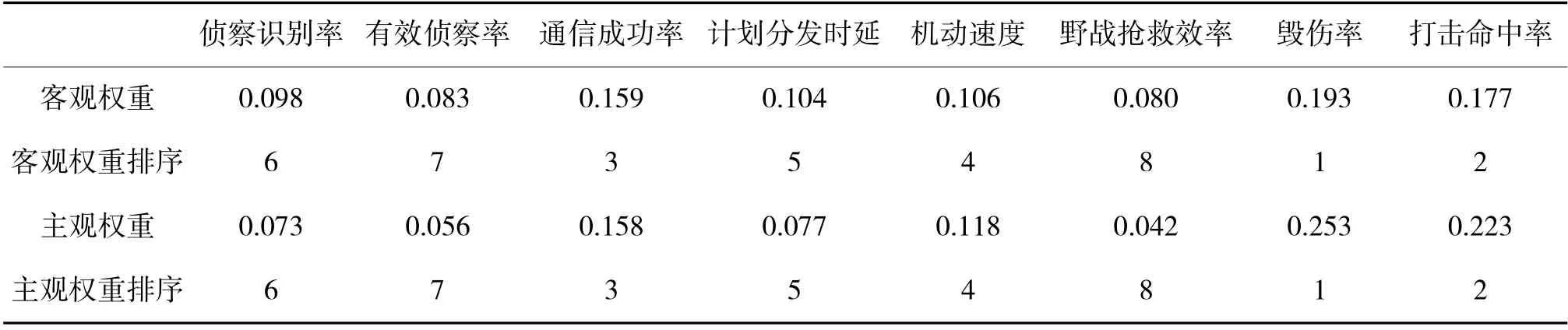
表4 组合权重的计算过程

由于方差和冲突性都为正向性指标，它们的值越大，则本文所构建的线性规划模型中的maxZ 就越大。

由改进方差最大化组合赋权法计算得到α、β分别为α=0.740，β=0.672，进而可以得到组合权重ω=αu+βv，再对ω=（ω，ω，ω，ω，ω，ω，ω，ω）进行归一化处理，得到归一化后的结果ω=（ω，ω，ω，ω，ω，ω，ω，ω）作为各个指标的最终权重。由方差最大化组合赋权法得到α、β 分别为α=0.719，β=0.695，也进行了权重归一化处理。改进法和原方法的各项指标的组合权重及其变化情况，改进法组合权重在保证指标的权重排序一致的基础上，综合考虑了各指标数据的离散程度和相关性，由表5 可知，通信成功率、机动速度、毁伤率、打击命中率4项指标的改进法组合权重增加，其余4 项指标的改进法组合权重下降。

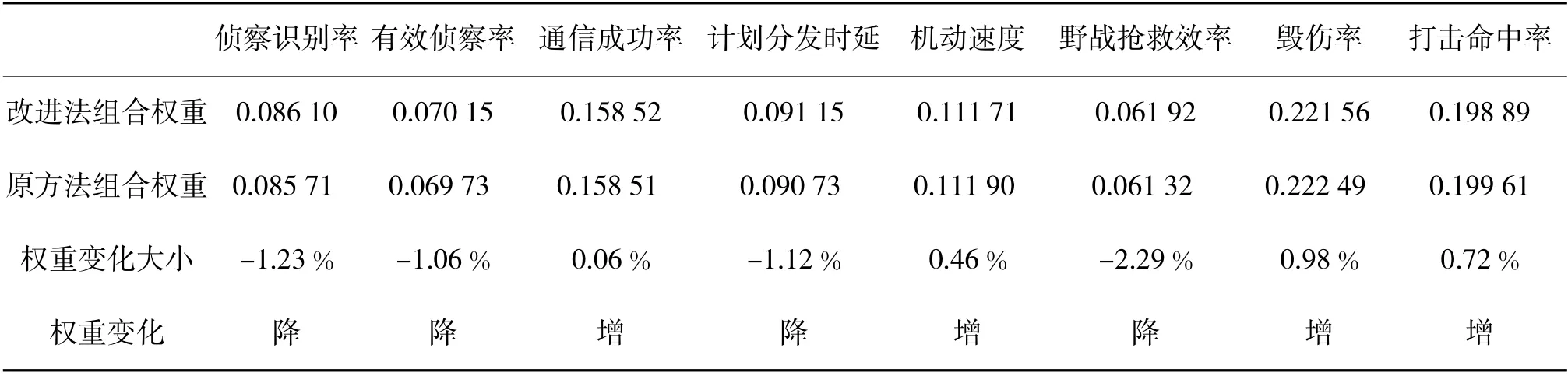
表5 组合权重对比

如果本例中的8 个指标在排序部分一致时，加入前5 个指标排序一致，则只对排序一致的权重对应的数据纳入线性规划模型中，使得maxZ 值最大。首先由改进方差最大化组合赋权法计算得到α、β分别为α=0.740，β=0.672，进而通过ω=αu+βv 可以得到组合权重ω，ω，ω，ω，ω，而ω，ω，ω只采用对应指标的主观权重，构成ω=（ω，ω，ω，ω，ω，ω，ω，ω），然后对ω 进行归一化处理，得到归一化后的结果ω=（ω，ω，ω，ω，ω，ω，ω，ω）作为各个指标的最终权重。

4 结论

为了组合权重的客观合理性，本文构造了一种改进方差最大化的组合赋权法，将指标本身的离散程度和指标之间的冲突性结合确定组合权重。为了使组合权重更加客观合理，首先考虑了样本数据的代表性和主客观权重排序的一致性，在排序完全一致的情况下，采用组合赋权法计算指标权重；在排序部分一致时对部分指标采用组合赋权法计算指标权重；在排序完全不一致时仍采用主观权重作为最终的指标权重。经过实例分析，本文可以为武器装备体系能力评估中的指标权重确定提供一种可靠的方法。