基于几何法的航迹关联算法研究

李 东，陈 健

（海军大连舰艇学院，辽宁 大连 116018）

0 引言

为了提高目标发现的概率和准确率，一艘舰艇通常都会安装尽可能多的探测设备，不同的探测设备对同一目标所记录的航迹通常不会完全重合，同一目标的不同航迹最终都会在相同时间汇集到信息中心。为了后续对目标航迹进行航迹融合，中心系统需要对不同探测设备返回的航迹信息加以判断或检验是否属于同一目标，也就是通常所说的航迹关联。

航迹关联的理论方法有很多，包括基于统计概率的关联方法，基于信号处理的方法，基于目标优化约束的方法，基于模糊综合决策的关联方法等，这些方法都是将航迹作为一个整体进行分析，并且都是在一定数量样本点基础上。而实际应用中，航迹点都是实时更新、实时传送的，并且战场态势下对于关联速度也有很高的要求，所以，这些方法在工程应用上存在一定的弊端。本文提出的航迹关联算法基于几何图形，对航迹点数量没有要求，并且可以实时地随着点迹的增加累积计算，不需要每次接收数据都重新对整个航迹进行计算，大大节省了计算时间，在此基础上还提出了航迹简化算法，进一步降低了计算复杂度，可以很好地应用到工程实践中。

1 航迹关联算法及编程实现

进行航迹关联的最终结果是要呈现关联航迹的相似度，在这里将相似度定义如下：

把其中一条航迹（以下称作航迹1）当作一条具有一定宽度的长带（如下页图1 所示），计算实时另一航迹（以下称作航迹2）在长带中的长度与其总长度的比值即为相似度。

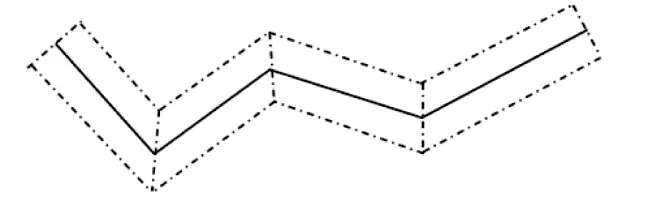
图1 梯形带

1.1 梯形带顶点的计算

最开始出于简单考虑，把每段线段对应的区域看作一个矩形，如图2 所示，但是由于一些缺口的存在，导致在实际操作中计算结果误差较大。所以，使用梯形（如图1 所示）代替矩形，来保证结果的准确性。在距离航迹1 的每一条航迹段上、下w（w 为梯形带宽度的一半，在实际应用中，w 的选择应该综合考量探测设备的测量精度，以及目标的速度、类型等属性，结合实际的航迹数据，通过归纳总结得到的值会更加精确）处分别做平行线。在航迹1 同一侧的所有平行线相交而成的折线段序列即为梯形带的一边，如此形成的两条折线段序列围成航迹1 的梯形带（梯形带的始末两个梯形均为直角梯形）。所以首先要计算每个梯形的顶点。

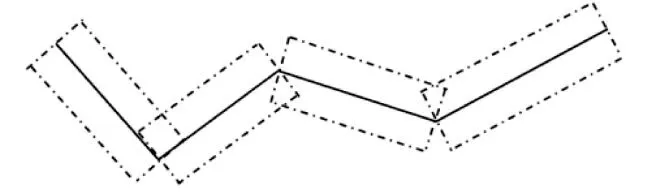
图2 矩形带

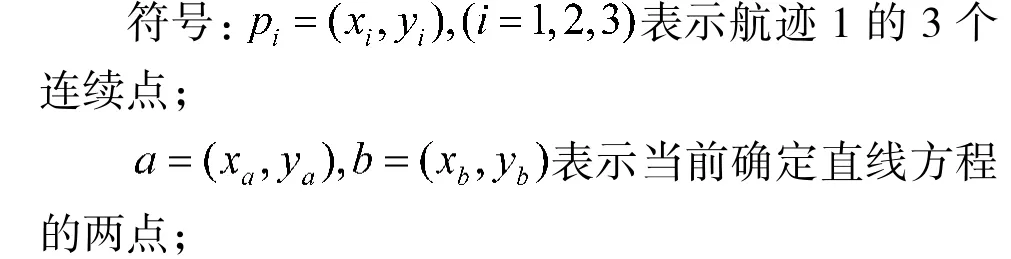
梯形带一边所在直线的一般式方程（Ax+By+C=0）中，常量均用符号C表示，另一边所对应的所有直线一般式方程中常量均用C表示。与一条直线平行且距离相等的直线有两条，区别是C 的不同，梯形带两边对C 的选取是难点。解决方法是利用航迹点的先后顺序，给两个航迹点所形成的线段赋予方向。利用线段的方向来解决带两边C、C的选取问题（如图3 所示）。该方法编程设计如下：

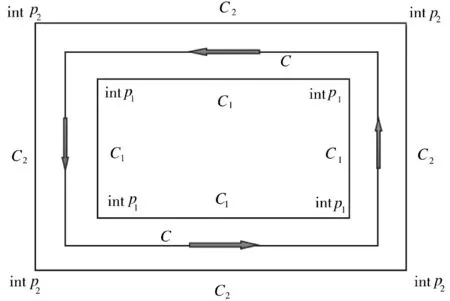
图3 C1、C2 的选取

输入：航迹1

输出：梯形2 顶点（梯形带同一侧交点均用intp1 表示，另一侧交点均用intp2 表示）

伪代码：

1.2 梯形顶点再存储

梯形顶点按上述算法“梯形顶点生成算法”输出后，进行重新存储（4 个顶点为一个单位，逆时针存储，为“一条线段在一个梯形内的长度计算算法”输入做准备），简略算法如下：

第1 次输入原顶点集合中连续的前4 个点，将第3 个和第4 个位置的点相互调换后，输出这4 个点；第k 次输入原顶点集合中的第2k-1 到第2k+2个点，将第3 个和第4 个位置的点相互调换后，输出这4 个点；当k=n-1 时，输出后结束（2n 表示原顶点集合中顶点个数）。

1.3 一条线段在一个梯形内的长度计算

要计算一条航迹和一个航迹带的相似度，则必须计算这条航迹所有航迹段在航迹带内的总长度，这个过程的单位过程即是计算一条线段在一个梯形内的长度（如下页图4 所示）。

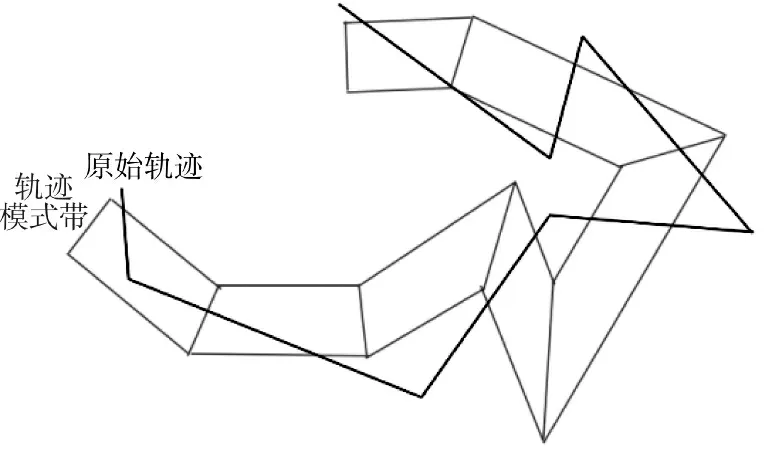
图4 相似度计算示意图

通过判断梯形的4 个顶点和线段所在直线的3种位置关系（顶点在直线上，在直线两侧，在直线一侧）以及分别满足这3 种位置关系的顶点个数来判断线段是否有在梯形内的部分，若是，求出线段在梯形内的长度；否则，输出长度为0。算法思路如下：

符号：

5）d 表示求得的线段在梯形内的长度。

通过判断线段所在直线与梯形的两个交点及线段的两个端点这4 个点的位置关系，来计算线段在梯形内的长度。利用夹角在（0°，180°］之间的两个共线（此处指在同一条直线上，而不仅仅是平行）向量间的位置关系，来计算两个向量重合部分的大小。

伪代码如下：

输入：梯形4 个顶点，线段两个顶点

输出：线段和梯形的相交长度

步骤：

Step 2：判断：若所有梯形顶点均在线段所在直线l 的同一侧，或者只有一个梯形顶点在直线l 上，而其他顶点在直线l 的同一侧，则输出d=0，转Step 10；否则，转Step 3；

Step 3：判断：若只有两个梯形顶点在直线l 上，另外两个顶点在直线l 的同一侧，转Step 7；否则，转Step 4；

Step 4：判断：若只有一个梯形顶点在直线l 上，其他3 个顶点分布在直线l 的两侧，转Step 8；否则，转Step 5；

Step 5：判断：若只有两个梯形顶点在直线l 上，其他两个顶点分布在直线l 的两侧，转Step 7；否则，转Step 6；

Step 6：除了Step 1 到Step 5 的情况外，剩下的情况是4个梯形顶点分布在直线l 的两侧，即直线l 与梯形的两边相交，转Step 8；否则，输出“出错”，转Step 10；

Step 7：判定在直线l 上的两个梯形顶点，分别记为int p、int p，转Step 9；

Step 8：计算直线l 与梯形的两交点int p、int p；

Step 9：判断int p、int p、a、b 这4 个点在直线l 上的先后位置关系，求得两条线段int pint p和ab 重合部分的长度d即为线段ab 在梯形内长度，输出d，转Step 10；

Step 10：结束。（如图5 所示）

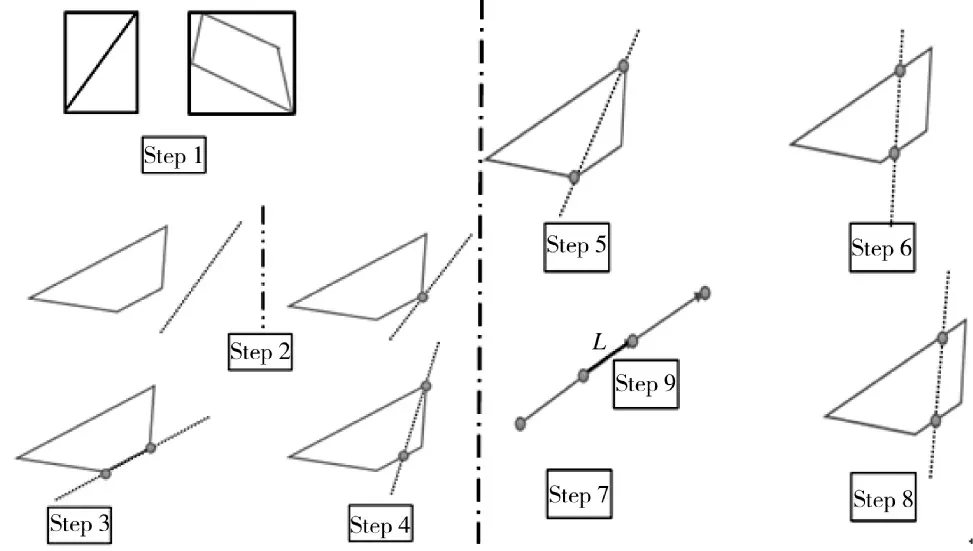
图5 线段在梯形内长度求解示意

1.4 实验验证

实验先模拟生成一条航迹（如图6 所示），然后对航迹上的每个点做随机浮动，生成50 条新航迹（如图7 所示），将这50 条新航迹与原始航迹做匹配求相似度（图8 为某一条航迹与原航迹的比较）。之后改变航迹的梯形带宽度，再分别计算相似度，得到了预期的结果，证明了算法的正确性。

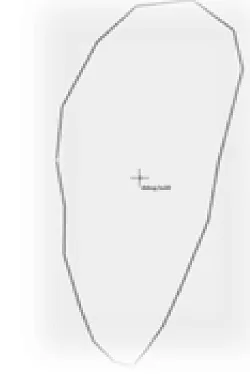
图6 原始航迹

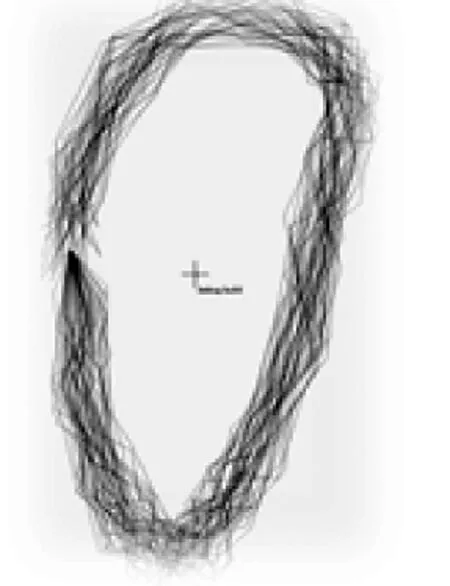
图7 新航迹生成

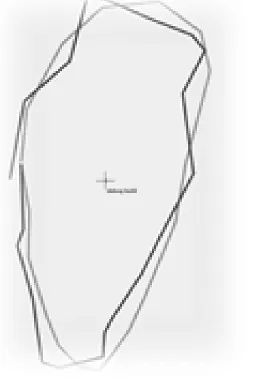
图8 相似度计算

2 航迹简化

采用1 中的算法进行航迹关联时，航迹点的数量成为影响算法速度的主要因素，尤其现在的探测设备采样频率普遍较高，收集到的航迹点比较密集，数量巨大。因此，为了能更好地适应战场需求，减少计算时间，本文提出如下算法对航迹进行简化，删除那些对构建梯形带影响较小的航迹点，抽取其中的关键点用作关联计算。

若连续的多个点几乎在一条直线上，则中间的点可去掉，如此即能用一条线段代替原来的多条折线段。因此，算法基本思想如下：

1）连续3 个采样点，判断中间一个采样点是否舍去（如图9 所示）。

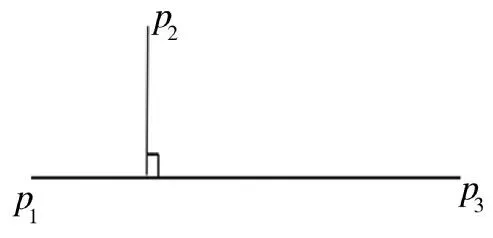
图9 单采样点取舍

过第1 个和第3 个采样点做一条直线，计算第2 个采样点到直线的距离，若该距离小于距离阈值（事先给定），则舍去第2 个采样点；否则，保留第2个采样点。

2）连续n 个采样点（n＞3），判断倒数第n-1 个采样点是否舍去（如图10 所示）。

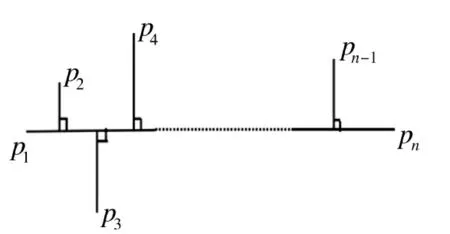
图10 多采样点取舍

过第1 个采样点和第n 个采样点做一条直线，分别计算中间n-2 个采样点到直线的距离，若所有距离均小于距离阈值，则舍去第n-1 个采样点；否则，保留第n-1 个采样点。

符号：

p、p代表两个航迹点，s、e 是点的下标，s 小于e，p为p、p之间的某个点，d为p距离p、p连线的距离，d为距离阈值。

输入：航迹点，d

输出：简化后的航迹点

算法伪代码如下：

本次实验通过一些测试数据进行检验，测试数据都是人造的航迹点。图11 和图12 是某次测试数据的简化前后散点图。

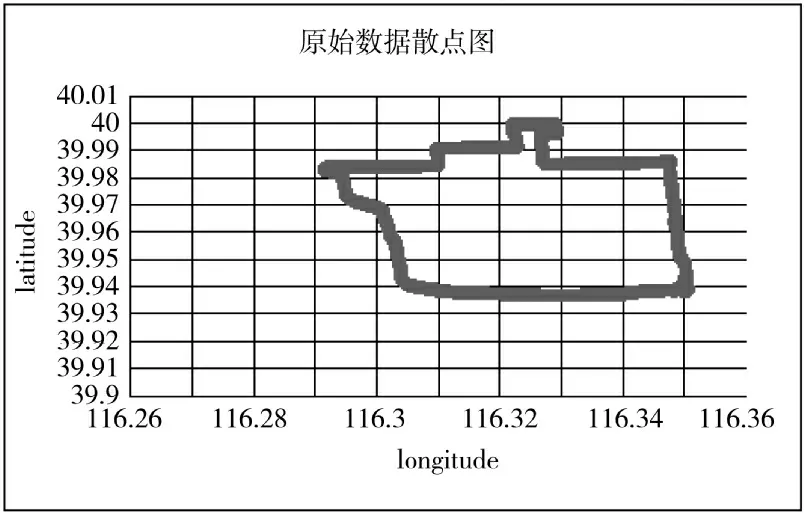
图11 简化前

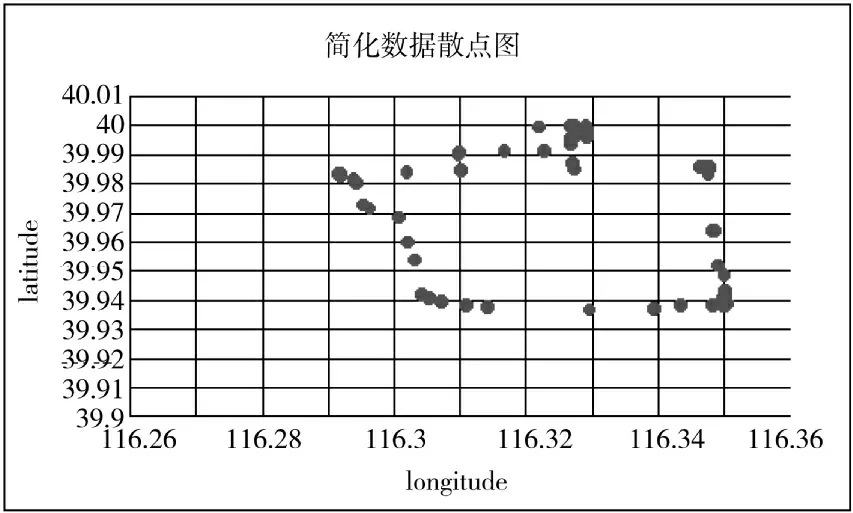
图12 简化后

从图中可以明显看到，简化后的航迹点少了很多，并且关键点也基本都保留了下来，所以算法的正确性基本得到验证。

3 结论

本文主要提出了一种基于几何法的航迹关联算法，在此基础上通过提出一种航迹简化方法提高了该算法的计算效率，并给出了编程实现的方法，设计实验验证了算法的准确性。与其他航迹关联算法相比，该算法从最直观的图形角度出发，不依赖航迹点的数量，可以实时对航迹进行关联，计算复杂度低，非常适合工程上应用。