Multiple model predictive control of perching maneuver based on guardian maps

Rui CAO, Huiwen WAN, Zhen HE, Yuping LU

College of Automated Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China

KEYWORDS Guardian maps;Model predictive control;Multi-Model switching rule;Online comprehensive design;Perching maneuver

Abstract Considering the strong nonlinearity of Unmanned Aerial Vehicles (UAVs) resulting from high Angle of Attack(AOA)and fast maneuvering,we present a multi-model predictive control strategy for UAV maneuvering, which has a small amount of online calculation. Firstly, we divide the maneuver envelope of UAV into several sub-regions on the basis of the gap metric theory. A novel algorithm is then developed to determine the ploytopic model for each sub-region.According to this, a Robust Model Predictive Control based on the Idea of Comprehensive optimization (ICE-RMPC) is proposed. The control law is designed offline and optimized online to reduce the computational expense. Then, the ICE-RMPC method is applied to design the controllers of sub-regions. In addition, to guarantee the stability of whole closed-loop system, a multi-model switching control strategy based on guardian maps is put forward. Finally, the tracking performance of proposed control strategy is demonstrated by an illustrative example.

1. Introduction

In recent years,Unmanned Aerial Vehicles (UAVs) have been rapidly developed and widely used. Among many types of UAVs,fixed-wing UAV has obvious advantages in endurance,flight range, and cruise speed.The fixed-wing aircraft generally adopts the landing method of running, landing net or parachute recovery. The shortcomings of these landing methods include large space requirements, difficulty in determining landing points, and complicated auxiliary landing devices, which greatly reduce the utilization rate of fixedwing UAVs.In recent years, inspired by the bird perching maneuvers,fixed-wing UAV has begun to emulate this landing method, hoping to land accurately at the designed position with less energy.The perching maneuver method can break through the limitation of fixed-wing UAV landing mode and improve its application range. Ref.designed a small glider and experimentally verified the feasibility of fixed-wing UAV landing on an electric wire. At present, the control problems of the perching maneuver of UAV have received more and more attention. For fixed-wing UAVs, perching maneuver is not an easy task.On the one hand,perching maneuvers require UAV to decelerate rapidly at high Angle of Attack (AOA) to reach the preset point within a specified time (in seconds),which resulting in the highly nonlinear and time-varying of UAV.On the other hand,high control performance is in great demand, including landing on a desired perching point with relatively high precision. Thus, it is a challenge for fixedwing UAV to accomplish perching maneuvers, especially the initial state deviations and model uncertainties are considered.

Due to the disturbances and uncertainties of actual system,the research of Robust Model Predictive Control(RMPC)has become a hotspot of model predictive control researches.Ref.used a Nonlinear Model Predictive Control(NMPC)to design the perching maneuver control law. The results showed that NMPC can process optimized trajectories, and had good performance in model error correction and anti-disturbance.However, the complexity of NMPC design makes it difficulty to implement in real-time flight control. The polytopic model is an effective way to describe uncertain systems, and is also a main research object of RMPC in recent years. Refs.adopted a single feedback law as the control strategy, which usually brought the conservativeness of controller design. If a control law sequence with the change of actual state can be obtained online, the Degree of Freedom (DOF) of RMPC would be improved, thereby optimizing the control performance and expanding the feasible range of system.Based on this idea,Leeand Casavolaet al proposed the concept of periodic invariant set, and a control law sequence was used to design the RMPC(this method was called Single Lyapunov Robust Model Predictive Control (SL-RMPC). However, in the SL-RMPC method, the single Lyapunov function and the periodic limit also brought the inevitable conservativeness of controller design. Then, Refs.presented a new approach based on multi-Lyapunov functions, in which each vertex of polytope model has a corresponding Lyapunov function. This method was named as the Parameter-Dependent Lyapunov Robust Model Predictive Control (PDL-RMPC)method. The PDL-RMPC method could expand the controllable area and improve control performance, but it brought a large amount of online calculation. In summary, for the robust model predictive control, the requirements on its control performance, online calculation amount and feasible region are contradictory.Therefore,how to effectively balance the three performances of small computation, good control ability and large feasible region to design a new RMPC strategy has become a difficulty and hotspot of model predictive control research in recent years.

To solve the design problem of robust model predictive controller for uncertain systems, an online comprehensive design method (robust model predictive control based on the idea of comprehensive optimization, referred to as ICERMPC) is proposed here. In the ICE-RMPC method, most of the calculation is transferred to off-line,so the online calculation load is reduced. The ICE-RMPC method provides an effective way to balance the contradiction between control performance, feasible region and online calculation amount. The gap metric theory is introduced to divide the flight envelope into different sub-regions and build linear models. Then, the ICE-RMPC method is used to design the controller of each sub-region. Further, a Guardian Map based ICE-RMC(GM-based ICE-RMPC) strategy is proposed to improve the switching performance and ensure the robust stability of the whole closed-loop system, which is composed of ICE-RMPC algorithm and GM-based switching rule.

The rest of the paper is organized as follows. In Section 2,the dynamic model of aircraft performing perching maneuvers is presented and the piecewise polytope model of UAV is constructed.Section 3 givens detailed step to design an online synthesis control strategy. Simulations results are described in Section 4 to verify the control performance. Finally, conclusions are drawn in Section 5.

2. Piecewise linearization

2.1. Kinematic model of the UAV

In this paper, the longitudinal motion of UAV is considered,which adopts the aerodynamic model in Refs.. The longitudinal motion equations of fixed-wing UAV can be expressed in the wind axes as

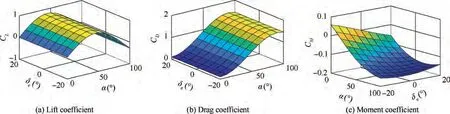
Fig. 1 Aerodynamics of the reference aircraft model.

2.2. Linear model construction based on gap metric

To design RMPC for perching maneuver, the first is to determine how many and which linear models are selected to describe the dynamic response of whole maneuver process.The most popular used method to construct a linear model set is trial and error strategy, that is, linear models are preselected, and will be replaced or reduced online based on the simulation results until satisfactory performance is obtained.This strategy usually has model redundancy and is timeconsuming.To solve the model selection problem,the gap metric theory is considered to analyze the relationship between linear systems, and then to obtain the model bank without prior linear models.

Let H be a finite dimensional linear system. The gap between two systems Hand His defined as

where,*denotes complex conjugation, ^Π represents the transfer function of Π. The detailed calculation and process of proof for gap metric can be referred to Ref..

For a fixed reference trajectory,the linear model of aircraft is directly related to the flight time. Therefore, the problem of dividing the flight envelope can be converted into dividing the time range. Considering the properties of gap metric, the procedure to select linear models is formulated as follows.

Select time point based on gap metric Step 1.Set the sampling time^t to obtain enough sampling points in the flight time range (the number of sampling points is denoted as Ng).Then,linearize the nonlinear system(2)around these points to obtain the linear models Pi， i=1，2，...，Ng（）.Step 2. Calculate gap values between linear models and a Ng×Ng gap-matrix δ～Hi，Hj■■Ng×Ng is obtained,where δ～（，）is（）the gap metric value.Step 3. Prescribe a distance level τ. Compare ∑（）with τ beginning with the i=1, j=i+1 to j=Ng. If j=i+1 δ～Hi，Hj（）>τ, then the corresponding linear models in the time range ［i^t， k^t］ is divided into the sub-interval∑k j=i+1 δ～Hi，Hj Γki］.Step 4.Set i=k+1 and repeat Step 3 until i=Ng-1.Suppose the total number of sub-regions obtained is Ns.Step 5. Select nominal points. The point satisfying= Hi，Hi+1，...，Hk［（）， j=i+1，i+2...，k is selected as the nominal point of sub-interval Γki, which can represent the min∑k s=i δ～Hs，Hj dynamic characteristics of aircraft in this sub-interval Γk i.Finally, the linear models corresponding to Ns nominal points are constructed to approximate the nonlinear model in the whole perching process.

Remark. To guarantee the convergence of discretization error,combining with related Refs., we give some suggestions on the selection of sampling time ^t:

A) The^t needs to satisfy Nyquist-Shannon sampling theorem.

B) The sampling frequency of flight data is usually higher than 50 Hz, as rigid body dynamics upper bound is usually 2 Hz.

C) The sampling step length should ensure that the stable region of aircraft has a high overlap rate in the adjacent sampling states.

The linear model at each nominal point is obtained by linearizing the nonlinear dynamics (2) along the reference trajectory （x，u） with the Jacobi linearization method. Then, the solution process of Linear Parameter Varying (LPV) model is as follows:

2.3. Transforming LPV into polytopic form

The ［t， t］ is defined as the time range of perching maneuver.Assume that N points ｛ t，t，...，t，...，t｝ , t= tare selected over the entire time domain via gap metric.According to Eq. (6), the linearization model at time point tis obtained as follows:

3. Robust model predictive control based on guardian map

In this section, a GM-based ICE-RMPC strategy for the perching maneuver control is given, which has low computational overhead. The strategy consists of two parts: one is the ICE-RMPC algorithm to realize comprehensive optimization in three directions: Control performance, initial feasible region, and online calculation; and the other is the improved switching rule based on GM to ensure smooth switching. It is shown in Fig. 2.

3.1. Algorithm description

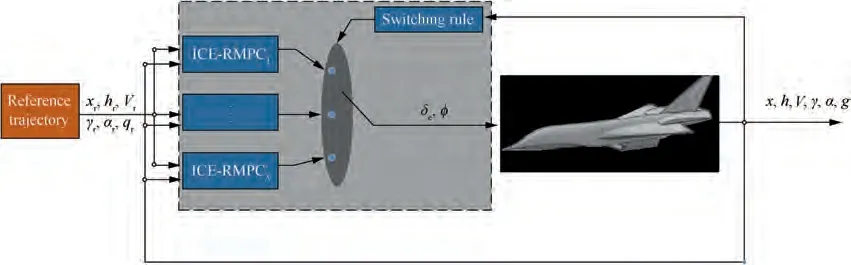
Fig. 2 Framework of GM-based ICE-RMPC strategy.

Fig. 3 Terminal constraint set based MPC.

Therefore, when Eqs. (31)-(34), (37), and (39) hold, the uncertain system (17) satisfies the control constraint (3) and is robustly asymptotically stable.

Due to the parameter-dependent Lyapunov function(22)is introduced, the number of variables and Linear Matrix Inequalities (LMIs) increase at each moment, and the amount of online computing becomes a huge burden,which is not conducive to real-time control of UAV.

It can be known from the optimization control problem(20)that Eqs.(31),(32),(37),and(39)only need known information. Therefore, χ，δ，G，Y，U，Qcan be calculated offline first, and then δis optimized online to obtain the control law K. Based on the idea of ‘‘offline design, online optimization”,we proposed an ICE-RMPC method, which can lighten the burden of online computing. Applying this method, the tracking maneuver control can realize comprehensive optimization of control performance, initial feasible region, and online calculation.The design idea of the ICE-RMPC method is as follows:

Moreover, the design steps of offline and online for ICERMPC are shown in Algorithm 1.

Algorithm 1. ICE-RMPC algorithm Offline:Step 1. For the p-th subsystem of perching maneuver, the attractive region G1p of the polytopic model is selected as the objective function.Under the constraints(31),(32),(37)and(39),the δ1 and N1 are chosen to solve the following optimization problem to obtain the first set of Q1p，Y1p，U1p.min■■■ ■Q1p，Y1p，U1p J=-log det G1 p s.t. Eqs. （31），（32），（37），（39）where N=N1，Qp =Q1p，Yp =Y1p，Up =U1p，χ=χ1，δ=δ1，G1p =Q1 p，j j=1，2，...，L）.Step 2. For the p-th subsystem, choose the δ2 δ2 ≪δ1（（）, N2 and deal with the optimization problems below to acquire the second set of Q2p，Y2p，U2p:min■■■ ■Q2p，Y2p，U2 J=-log det G2 p p s.t. Eqs.（31），（32），（37），（39）where N=N2，Qp =Q2p，Yp =Y2p，Up =U2p，χ=χ2，δ=δ2，G2p =Q2 p，j j=1，2，...，L）.Online:Step 1. The subsystem at time p is determined;Step 2. The system status at time p is measured;Step 3. The following online optimization problem is solved to get the control law Kp of subsystem at time p:min（（）s.t. （33），（34） with Qj =Q～j δ0，u～（k ），λ1，...，λN1，...，λN1+N2 J=δ0+ λ1+...+λN1（） δ1+χ1（）+ λN1+1+...+λN2（） δ2+χ2∑N1+N2-2(40)i=1λi ≤1，λi ≥0 i=1，2，...，N1+N2-2）（Q～j =λ1G11+...+λN1Q1N1-1，j+λN1G21...+λN1+N2-1Q2N2-1，j

3.2. Switching rule based on guardian maps

where Ris a set of n×n real matrix,S（Ω ）denotes closure of the set S. Some guardian maps for classical regions are shown in Ref..

The control law of the whole perching maneuver can be adaptively obtained by using this switching rule.It can be realized because the linear model constructed by gap metric theory ensures that the stability region of two adjacent systems has overlapped part in advance.

3.3. Design of model predictive controller

The linear model set is constructed via Section 2 to approximate the nonlinear system of perching process. On this basis,the design process of the controller is as follows(Algorithm 2):

Algorithm 2. The GM-based ICE-RMPC algorithm Step 1. Pretreatment: The χ1，δ1，～F11，～F12，...，～F1N■■■and χ2，δ2，～F21，～F22，...，～F2N■are designed along the reference trajectory based on the offline part of Algorithm 1. Let the stability set be S-mc Ω（ ）, which depends on the designer.Step 2. Initialization: Set tk =t0.Step 3. Calculate the control law Kk via the online part of Algorithm 1 that enables robust asymptotic stability at time tk.Step 4.Calculate the largest stability domain Θk = t-k，t+（）under the control law Kk based on the setting S-mc （Ω ）.Step 5. If tk+1，tk+2 k［］∉Θk, let k=k+1,tk =min tk， tk-1+t+）and return to Step 3 to update the controller; otherwise, continue using the current control law and returning to Step 4 to update the stable region Θk, and let k=k+1.Step 6. Determine whether the tN ∈Θk. If it does, then stop.Otherwise, repeat Steps 3-6.（（）/2 k-1

Then, a piecewise linear control law can be obtained, according to the above steps:

3.4. Stability analysis

4. Simulation study

In this section, the tracking ability of SL-RMPC,PDLRMPC,and ICE-RMPC (Algorithm 1) are simulated and compared to verify the effectiveness of ICE-RMPC algorithm.Moreover, ICE-RMPC and GM-based ICE-RMPC (Algorithm 2) are also simulated to analyze the switching ability and tracking accuracy of GM-based ICE-RMPC algorithm.

4.1. Simulation conditions

The main characteristics of the fixed-wing UAVused for simulation are as follows: m=0.8 kg, I=0.1 kg·m, and reference area S=0.25 m. Considering the perching time is [0,1.5 s], which means the UAV needs to reach the perch point in 1.5 s. The UAV’s thrust is assumed to be constant, and the pseudo-spectral methodis used to design the perching maneuver reference trajectory. The control constraints of UAV are shown in Eq. (49).

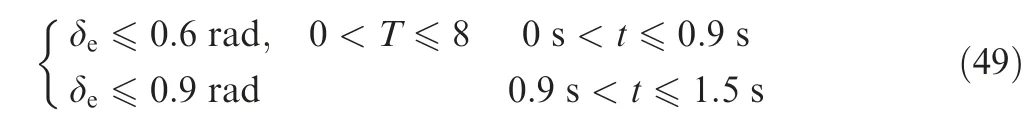
Before designing the controller, a LPV model that can describe the nonlinear system is established by adopting the gap metric theory. First, select the sampling time ^t to be 0.01 s, and the gap value between two adjacent systems (indicated by the blue dot) is calculated. Then, set the threshold τ=0.1 to divide the sub-interval (indicated by the red solid line).Finally,the nominal point(indicated by the red*)is chosen to represent the sub-area.Based on the nominal points,the

In addition,the stability set S（Ω ）= ｛p，ξ，ϖ｝in Algorithm 2 as shown in Fig. 6. p=-1.5 represents the maximum real axis; ξ=0.6235 is the minimum damping ratio; ϖ=20 denotes the maximum natural frequency.

4.2. Simulation results and analysis

Table 1 shows the computation times of ICE-RMPC algorithm and PDL-RMPC algorithm to obtain single control law.It can be concluded that the ICE-RMPC algorithm can greatly decrease the computational expense.

Fig. 4 Select point via gap metric.

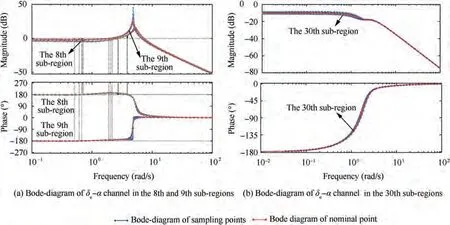
Fig. 5 Bode diagram of sub-regions.

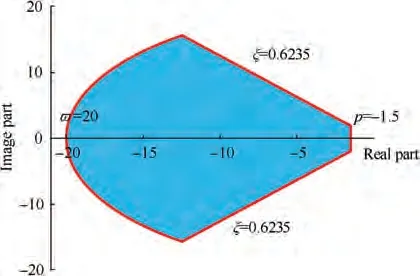
Fig. 6 Stability set S-m （Ω ）.

As can be seen from the speed and height tracking curves in Figs. 7 and 8, the PDL-RMPC method has better tracking effect than the SL-RMPC method under the initial error e.In addition, according to Fig. 7 and the description of ICERMPC algorithm, although the offline part of the Algorithm 1 has a little relationship with the state, improper parameter selection(｛δ，N，δ，N｝)would affect the online design effect.That is,the improvement of calculation efficiency would sacrifice a certain tracking accuracy. In Fig. 9, the elevator deflection and thrust input are all kept within set control constraints (49).

Moreover, based on the pitch rate change curves in Fig. 8 and control curves in Fig. 9, we can see that the control law of PDL-RMPC or ICE-RMPC would cause the unsmooth transition, thereby degrading the control performance of system. To further improve the tracking accuracy and switching smoothness of ICE-PMPC algorithm, a GM-based ICERMPC control strategy is proposed in this paper.

Figs. 10 and Fig. 11 describe the tracking curves of PDLRMPC, ICE-RMPC and GM-based ICE-RMPC (the control law is adaptively switched based on GM theory) under uncertain parameters and initial error e. In both methods, the parameters are set as δ=1000，N=1，δ=10，N=1.

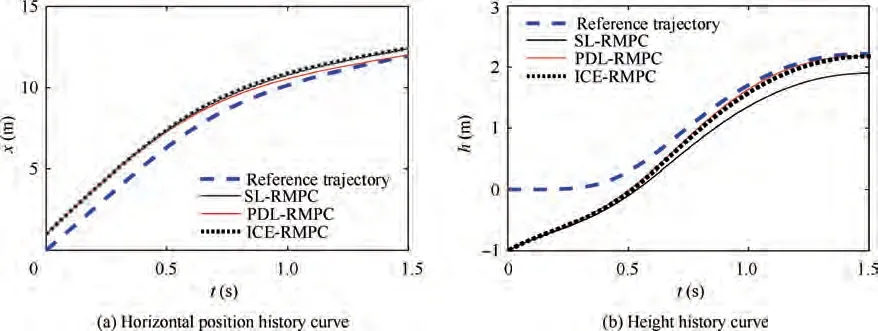
Fig. 7 Trajectory histories with parameter uncertainty and initial error e1.

Fig. 8 State histories with parameter uncertainty and initial error e1.

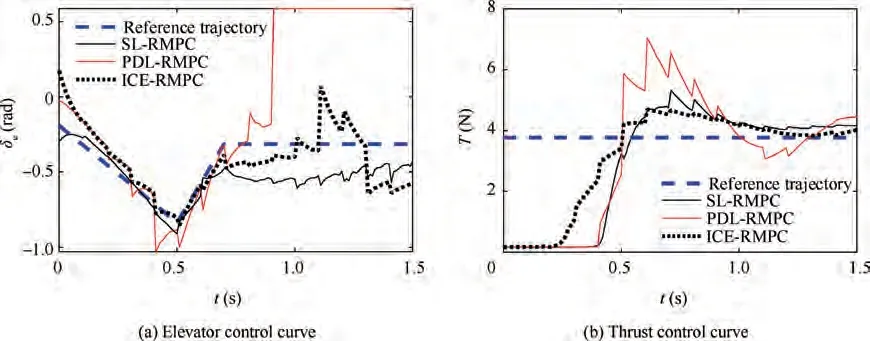
Fig. 9 Control inputs with parameter uncertainty and initial error e1.

From Fig.10 and Fig.11,it can be seen that the GM-based ICE-RMPC strategy can improve the tracking accuracy of the ICE-RMPC algorithm. In addition, according to the curve of pitch angle rate in Fig. 11, it can be known that the switching rule based on GM can ensure the smooth switching of transition process,thereby achieving better smoothness of the whole maneuver process. Fig. 12 shows the control curves under three robust model predictive control algorithms. Different from PDL-RMPC and ICE-RMPC, the control law is switched adaptively under GM-based ICE-RMPC algorithm.As can be seen from Fig. 12, the control curves obtained by GM-based ICE-RMPC strategy are smoother compared with the other two control algorithms and satisfy the control constraints (49).

In addition, the above simulation results indicate that the control input obtained by the GM-based ICE-RMPC strategy is closer to the reference control input (less additional control energy is required),and the control input curve is smoother.It can be seen from Figs. 10-12 that compared with other algorithms, the GM-based ICE-RMPC strategy can save the control energy required for tracking control and make the switching process smoother.

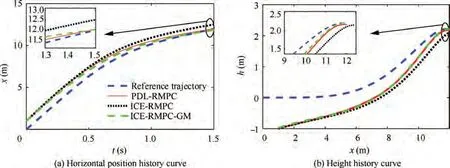
Fig. 10 Trajectory histories with parameter uncertainty and initial error e1.

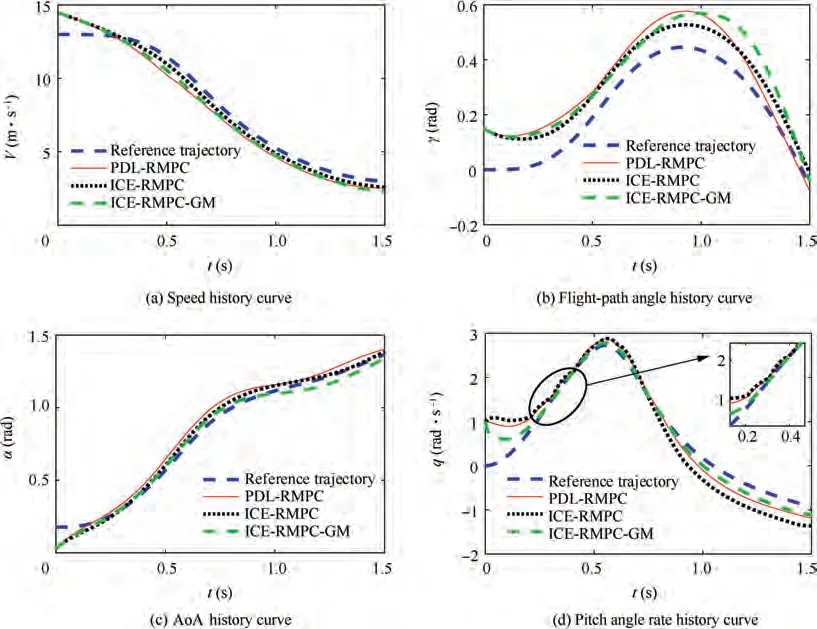
Fig. 11 State histories with parameter uncertainty and initial error e1.

Table 1 Calculation efficiency.

Table 1 also shows the simulation time of GM-based ICERMPC algorithm to get signal control law. According to Table 1,it can be concluded that the introduction of GM theory into the ICE-RMPC algorithm will not cause excessive online calculation.That is,the reduction in computational efficiency due to the improvement in performance is acceptable.

Fig. 12 Control inputs with parameter uncertainty and initial error e1.

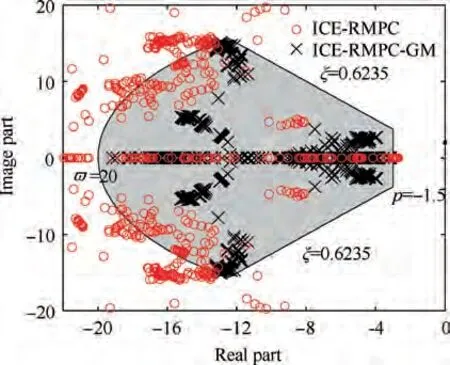
Fig. 13 Control inputs with parameter uncertainty and initial error e1.

Fig. 13 indicates the closed-loop pole distribution of fixedwing UAV under the ICE-RMPC algorithm and the GMbased ICE-RMPC strategy during the whole perching maneuver process.

According to Fig. 13, under the GM-based ICE-RMPC strategy, the poles of closed-loop system are all distributed in the stable set S（Ω ） during the perching maneuver process.The simulation results reflect that the GM-based ICE-RMPC strategy can guarantee the smoothness of the system transition process and the tracking accuracy in the presence of system uncertainty and deviation.

5. Conclusions

In this paper,a GM-based ICE-RMPC strategy was presented to design controller for the high-AOA perching maneuver of UAVs. The main contributions of the work can be concluded as: (A) Gap metric method was utilized to determine model bank, which made the constructed linear model can better reflect the motion characteristics of nonlinear system. (B)Improved switching rule, i.e. pre-switching based on guardian maps was employed for smooth switching. (C) GM-based ICE-RMPC strategy was proposed to ensure successful perching maneuvers and realize the smoothness of switching process, in the presence of both initial deviations and uncertainties. Among them, ICE-RMPC realized ‘‘offline design,online optimization”to reduce the online computation.

Simulation results in cases of uncertain parameters and initial deviations show the proposed control strategy can guarantee the success of perching maneuver and the smooth transition of the switching process, which prove the effectiveness of the control method.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

We thank the anonymous reviewers for their critical and constructive review of the manuscript. This study was cosupported by the National Natural Science Foundation of China (Nos. 61873126, 11572149).