Multiframe weak target track-before-detect based on pseudo-spectrum in mixed coordinates

Liangliang WANG, Gongjian ZHOU,*, Thiagalingam KIRUBARAJAN

a School of Electronics and Information Engineering, Harbin Institute of Technology, Harbin 150001, China

b Key Laboratory of Marine Environmental Monitoring and Information Processing, Ministry of Industry and Information Technology, Harbin 150001, China

c Department of Electrical and Computer Engineering, McMaster University, ON, Hamilton L8S 4K1, Canada

KEYWORDS Mixed coordinates;Multiframe detection;Pseudo-spectrum;Track-before-detect;Weak target detection

Abstract Traditional multiframe Track-Before-Detect (TBD) may incur adverse integration loss resulting from model mismatch in sensor coordinates.Its suboptimal integration strategy may cause target envelope degradation.To address these issues,a pseudo-spectrum-based multiframe TBD in mixed coordinates is proposed firstly.The data search for energy integration is conducted based on an accurate model in the x-y plane while target energy is integrated based on pseudo-spectrum in sensor coordinates.The algorithm performance is improved since the model mismatch is eliminated,and the pseudo-spectrum based integration facilitates well maintained target envelope.The detailed multiframe integration procedure and theoretical target integrated envelope are derived. Secondly,to cope with the unknown target velocity,a velocity filter bank based on pseudo-spectrum in mixed coordinates is proposed.The effect of velocity mismatch on algorithm performance is analyzed and an efficient method for filter bank design is presented. Thirdly, a parameter estimation method using characteristics of integrated envelope is presented for improved target polar position and Cartesian velocity estimation. Finally, numerical results are provided to demonstrate the effectiveness of the proposed method.

1. Introduction

The performance of conventional tracking methodsmay be degraded when the target Signal-to-Noise Ratio (SNR) is low, since the detection thresholding before tracking may discard weak targets. In contrast, Track-Before-Detect (TBD)techniqueshave an advantage of detecting and tracking weak targets through the direct use of unthresholded raw data.Classical TBD algorithms include Dynamic Programming based TBD (DP-TBD), Velocity Filtering based TBD(VF-TBD), Hough Transformation based TBD (HTTBD)and Particle Filter based TBD (PF-TBD).PF-TBD is a single frame recursive TBD, which can recursively estimate target state at each scan through the propagation of properly weighted particles. PF based methods in Refs. [4,29,31] are capable of providing a recursive solution for targets with complicated motions.

DP-TBD, VF-TBD and HT-TBD belong to MultiFrame TBD (MF-TBD) or batch processing based methods. MFTBD can increase target SNR by integrating target echo energy received within multiple consecutive frames and yield improved detection performance.MF-TBD methods were first proposed for weak target detection in optical and infrared images in Refs. [6,19,32]. Recently, some challenging issues in practical applications, e.g., multi-target processing in Refs.[14,33,34], homogeneous/nonhomogeneous clutter in Refs.[23,9,16,35], maneuvering target detection in Refs. [36,37],etc., are concerned.

HT-TBD methods are performed by transforming the detection of trajectory feature to the peak searching in parameter space. The first-threshold preprocessingused for transformation points extraction may discard some information of raw data.

In DP-TBD methods, multiframe integration is conducted by searching for the maximum value in the feasible region. DP-TBD methodshave an advantage of dealing with slowly maneuvering targets. The target integrated envelope may be extended to multiple cells in DP-TBD. This has an adverse effect on target detection and parameter estimation in Refs. [33,15,35].

VF-TBD in Refs. [8,21,20,18,19] performs energy integration by matching the constant target velocities in raw measurement plane without first-threshold preprocessing as in Hough transformation. The integrated target envelope of VF-TBD can be focused better than that of DP-TBD,and its fixed computational complexity helps with practical implementation.In traditional VF-TBD methods, the target echo value in a cell is added to the cell closest to its predicted position,without considering the target energy spillover. The target integrated envelope is degraded, which in turn affects parameter estimation using envelope characteristics. In Refs. [39,40],pseudo-spectrum approaches are proposed and applied to VF-TBD for multiframe detection of weak targets in the x-y plane.By constructing a pseudo-spectrum in each quantized cell, the spilled target energy can be utilized for energy integration and the integrated envelope can be well maintained. This promotes the improvement of detection performance. Precise parameter estimation can be conducted using characteristics of integrated envelope.

In contrast to optical and infrared images that generate measurements in Cartesian coordinates, the measurements in radar and sonar systems are provided in two-dimensional polar or three-dimensional spherical coordinates in Refs.[41,42].Although the state of a constant velocity target evolves linearly over time in Cartesian coordinates, its corresponding state evolution is nonlinear in sensor coordinates. In some DP-TBD methods, it is incorrectly assumed that the state of a target with constant Cartesian velocity varies linearly in sensor coordinates with time.The target energy is integrated based on the approximate linear model in these methods. The model mismatch may cause algorithm performance degradation. In Ref. [45], the evolution of target range-Doppler is described accurately, and a speed square filtering based method is provided to achieve accurate energy integration in radar range-Doppler plane. However, this method is limited to TBD for Doppler radars, and not capable of dealing with raw range-azimuth data effectively. Some radar or sonar sensors can only provide range and azimuth measurements. To achieve energy integration without model mismatch in polar coordinates, a mixed-coordinate-based three-dimensional matched filtering is presented in Ref. [46]. However, similar to the conventional algorithms, the suboptimal integration strategy may cause envelope degradation.Its performance is decreased when processing energy diffusion targets due to the discard of target spilled energy.

In this paper,a new Pseudo-Spectrum based TBD in Mixed Coordinates (MC-PS-TBD) is proposed for multiframe weak target detection and tracking in range-azimuth plane. The position of each measurement cell is converted into Cartesian coordinates and predicted according to an assumed Cartesian velocity in each direction. The predicted polar position is obtained by converting the above Cartesian prediction back to sensor coordinates. This mixed coordinate process avoids model mismatch resulting from inaccurate motion approximation and is beneficial to subsequent target energy integration.Then, a pseudo-spectrum is constructed with the predicted polar position as the center and measurement value of the cell as its peak. Samples of the pseudo-spectrum are added onto corresponding cells for energy integration. Consequently, the characteristics of target envelope can be maintained for precise parameter estimation. The integration procedure is presented detailedly and the theoretical target integrated envelope is derived.To match the unknown target velocity,a velocity filter bank based on pseudo-spectrum in mixed coordinates is presented. The μ-width of target envelope in velocity domain(i.e., the envelope width from the peak to the point whose value is μ times the peak one)is derived under the mixed coordinate framework.An efficient design of the filter bank is provided to reach a compromise between the conflicting system complexity and performance requirements. A precise parameter estimation method for polar position and Cartesian velocity is presented. Finally, the energy integration and computational complexity of the proposed MC-PS-TBD are analyzed.

In comparison with the traditional pseudo-spectrum based methods, the proposed MC-PS-TBD has some unique contributions. The conventional pseudo-spectrum based velocity filtering in Refs.[39,40]is presented for weak target detection in Cartesian coordinate sensors. The improved pseudo-spectrum based speed square filtering in Ref. [45] is used to detect and track weak targets in range-Doppler plane. However, none of these pseudo-spectrum approaches can effectively handle range-azimuth measurements.In contrast,this work addresses the problem of multiframe detection of weak targets in rangeazimuth plane. The unique contributions in this work can be summarized as:(A)A new pseudo-spectrum based multiframe TBD in mixed coordinates is proposed for weak target detection and tracking in range-azimuth plane. The energy integration process is presented in detail and the target integrated envelope is derived theoretically. (B) To cope with the unknown target velocity, a velocity filter bank based on pseudo-spectrum in mixed coordinates is proposed. The effect of velocity mismatch on the algorithm performance is analyzed. A method for efficient filter bank design is provided.(C) A method using envelope characteristics is presented for target polar position and Cartesian velocity estimation.Target echo integration and computational complexity are analyzed.

The remainder of the paper is organized as follows. The measurement model in polar coordinates is presented in Section 2, and the problem of MF-TBD in polar coordinates is also discussed. In Section 3, the proposed MC-PS-TBD is investigated in detail. Simulation results are provided in Section 4, followed by conclusions in Section 5.

2. Problem formulation

In this paper, we aim at deriving a strategy to effectively detect and track weak targets in range-azimuth plane. Multiframe integration used in MF-TBD is capable of improving the SNR of weak targets and enhancing their detectability.An accurate description of target motion in polar coordinates is important for multiframe accumulation. That is, the data search for energy integration is supposed to be performed according to the correct motion model instead of the approximate models in polar coordinates in Refs. [43,35,16,44]. In addition, due to the existence of target energy diffusion, it is of significance to make full use of the target energy on cells to enhance the detection probability. The target envelope degradation in existing MF-TBD methodsshould be alleviated through proper accumulation method.

3.Pseudo-spectrum based multiframe TBD in mixed coordinates

In this section, a new multiframe TBD method based on Pseudo-Spectrum in Mixed Coordinates (MC-PS-TBD) is derived to address the limitations of the conventional MFTBD methods discussed above.

3.1. Target state conversion

As illustrated in Eqs. (6) and (7), a target with a constant Cartesian velocity may not follow a CV motion in sensor coordinates. By matching the constant target Cartesian velocity in the filter, its predicted position in sensor coordinates can be obtained accurately in mixed coordinates. This accurate position prediction contributes to effective target energy integration.

3.2. Pseudo-spectrum based multiframe integration in mixed coordinates

The pseudo-spectrum sampling values on quantized cells are added to the Kth frame for multiframe accumulation.The final output is the accumulation result of all pseudospectra. Fig. 1 shows the schematic diagram of the proposed MC-PS-TBD, where the detection is conducted according to Neyman-Pearson Criterionand parameter estimation is introduced below. The pseudo code of MC-PS-TBD is provided in Algorithm 1 in detail, whereאandאdenote the sets of range and azimuth cells which may contain the target echo energy in frame k. The prior information of target position is usually unknown in practice,each quantized cell should be considered for processing.

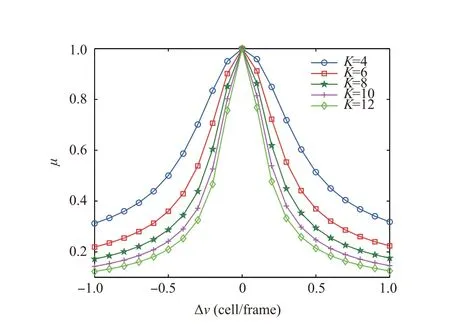
Fig. 2 Normalized value of integrated envelope in the velocity domain.

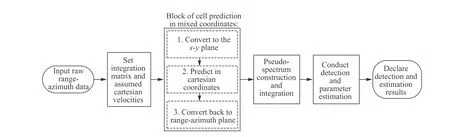
Fig. 1 Schematic diagram of the proposed MC-PS-TBD method.

Algorithm 1. Pseudo code of MC-PS-TBDimages/BZ_106_383_510_410_537.pngimages/BZ_106_826_510_857_537.pngimages/BZ_106_1092_510_1123_537.pngimages/BZ_106_816_1037_837_1057.pngimages/BZ_106_813_1085_834_1106.pngimages/BZ_106_857_1209_878_1230.pngimages/BZ_106_570_1528_597_1555.pngimages/BZ_106_774_1528_801_1555.pngimages/BZ_106_937_1534_958_1555.png

In short,the proposed integration procedure is summarized as follows: position prediction according to accurate model in Cartesian coordinates and pseudo-spectrum based multiframe integration in sensor coordinates.Due to the use of the mixedcoordinate approach, the predicted target position in polar coordinates can be obtained accurately and the integration loss resulting from model mismatch can be eliminated.The pseudospectrum based multiframe accumulation facilitates improved target energy integration and well-maintained target integrated envelope.

The proposed MC-PS-TBD has some advantages over traditional pseudo-spectrum based methods. The conventional pseudo-spectrum approach in Refs. [39,40] can only deal with weak targets in Cartesian coordinate sensors, and is incapable of handling polar coordinate measurements. In contrast, this work is presented to detect and track weak targets in raw range-azimuth measurement plane. The conventional pseudospectrum based speed square filter in Ref. [45] is presented for multiframe weak target detection in range-Doppler plane and cannot determine the target moving direction because only absolute value of target speed is matched.On the contrary,the proposed MC-PS-TBD is capable of producing estimation of both magnitude and direction of target speed by matching actual target velocity in each direction.Meanwhile,the following theoretical analysis of target integrated envelope, filter bank design and parameter estimation are different from conventional methods.

3.3. Pseudo-spectrum-based velocity filter bank in mixed coordinates

To deal with the unknown target velocity,a velocity filter bank based on pseudo-spectrum in mixed coordinates is presented in this subsection. In each filter of the bank, a unique velocity is considered as the potential target velocity. When the actual target velocity is matched with the assumed one, the filter can produce the maximum output.The target integrated envelope is derived theoretically, and the filter bank is investigated and designed in detail.

As derived in Refs. [38,5,18,46], the transfer function of VF-TBD in mixed coordinates can be expressed as

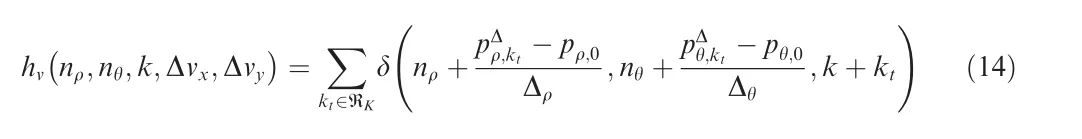
where

In addition,as illustrated in Fig.2,the normalized envelope in the velocity domain becomes narrow with increasing number of frames.The system with narrower envelope in the velocity domain can better distinguish targets with velocities. It is possible to enhance the velocity resolution by increasing the amount of frames.

3.4. Analysis of theoretical integrated envelope

As discussed above,confined by the complicated expressions in Eqs. (20) and (23), the integrated envelope is analytically intractable. In this subsection, these expressions are approximated to analyze the target envelope in both spatial and velocity domains. In addition, the μ-width of target envelope in the velocity domain is derived.An efficient method is proposed to design the velocity filter bank.

3.4.1. Analysis of the envelope in the spatial domain

Expanding Eq. (7) as a Taylor series and only retaining the first-order terms,the motion of the target in sensor coordinates can be approximated as

As illustrated in Eq. (34), the target integrated envelope is related to its echo envelope. We can obtain the characteristics of the integrated envelope through the known target echo envelope. This enables improved parameter estimation using envelope characteristics.

Note that the target motion approximation in Eq. (24) is reasonable when the target is in the far-field scenario of sensor. Nevertheless, for a target close to the sensor, this may lead to larger approximation errors, which has an adverse effect on integrated envelope approximation. In this case,the target envelope characteristics may be obtained inaccurately, causing performance degradation of parameter estimation using envelope characteristics. The influence of the approximation in Eq. (24) on parameter estimation will be evaluated later.

To alleviate the performance loss arising from velocity mismatch, the number of velocity filters should be large. But the system complexity increases with the number of filters. In Ref. [8], the gap between two filters is designed as the μwidth of target envelope in the velocity domain.Assuming that Δv=Δv=Δv, the μ-width can be obtained according to Eq. (45) as

3.5. Target parameter estimation

In this subsection, the target polar position and Cartesian velocity are estimated according to the adjacent-cell amplitude-comparison method in Refs. [45,39,49] using integrated envelope characteristics.

In the above, ln is the logarithm operator, Uand Uare the logarithms in range and azimuth, respectively.

The target position estimation in frame K can be obtained according to Eqs. (49) and (50) as

As discussed above, the position estimates are obtained according to the approximate integrated envelope in Eq.(34). However, the accuracy of the approximate envelope is influenced by the target’s radial distance. Thus, the position estimation accuracy will be affected by the radial distance. In Fig. 3, the estimation errors in Eqs. (55) and (56) are plotted against the radial distance with range resolution 1 km.As illustrated in Fig. 3, the error decreases as the radial distance increases. It is reasonable since the motion approximation in Eq.(24)is more accurate in the case that the target is far from the sensor. The calculation error is acceptable in dealing with targets close to sensor since the error is much smaller than the resolution property.

3.5.2. Cartesian velocity estimation

It can be found that the above Eq.(57)is a quadratic function with one variable in the x or y direction.The second order polynomial fitting is used to approximate the envelope in each direction. The envelopes in the x and y directions are respectively fitted as

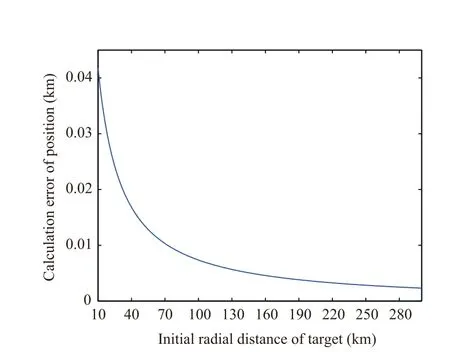
Fig. 3 Calculation error of position vs. target radial distance.

Fig.4 shows the envelopes fitted from different numbers of points Nin the velocity domain in one dimension, where N=2N+1.As illustrated in this figure, the polynomial fitting with three points (i.e., the cell with the highest value and the two beside it) yields good fitting performance around the peak position. Thus, we choose N=3 fitting points (i.e.,N=1) to fit the envelope in the velocity domain.

3.6. Discussions

3.6.1. Comparison of energy integration

Fig. 5(a)shows the normalized value of single frame measurement plane with an input SNR of 8 dB. Figs. 5(b) and 5(c)show the integration results from DP-TBD and the proposed method, respectively. As illustrated in these three figures, the target SNR can be improved through multiframe integration,which is beneficial to the detection and estimation of weak targets.

As illustrated in Fig. 5(b),the target integrated envelope in DP-TBD is degraded and extended to multiple cells. The extended envelopes may cause the mutual interference of targets, leading to algorithm performance degradation. In contrast, in Fig. 5(c), the target integrated energy in the proposed method is focused and the envelope can be maintained. This contributes to improved detection performance and enables precise estimation using characteristics of integrated envelope.

Since the pseudo-spectrum occupying multiple cells is constructed for each measurement cell to obtain energy integration, the integrated spectrum may be slightly expanded.However, as illustrated in Figs. 5(b) and 5(c), the envelope expansion in the proposed MC-PS-TBD is negligible compared to that in DP-TBD method.

3.6.2. Comparison of computational complexity

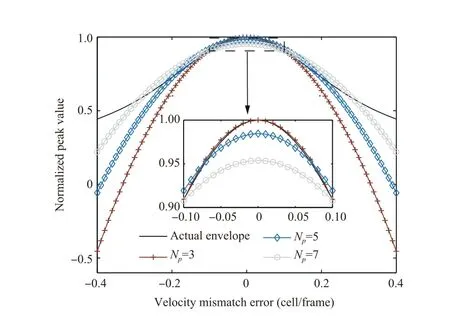
Fig.4 Polynomial fitting curves with different numbers of fitting points Np in the velocity domain.

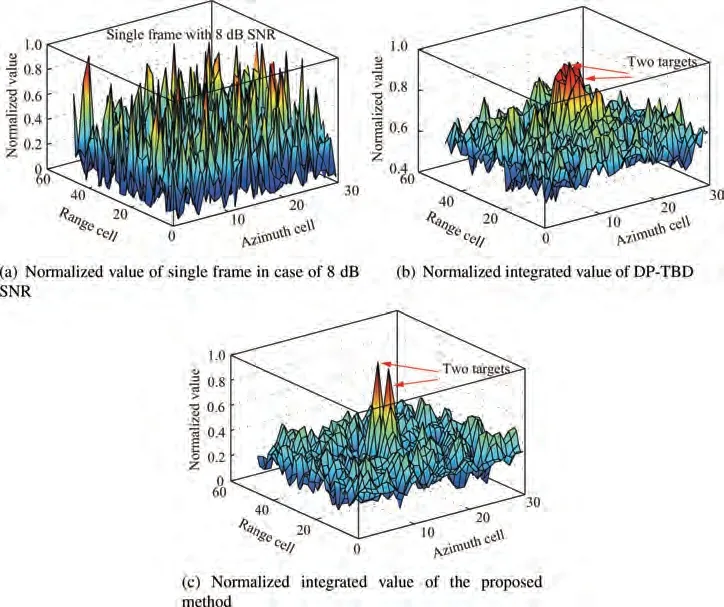
Fig. 5 Comparison of energy integration in the presence of two targets.

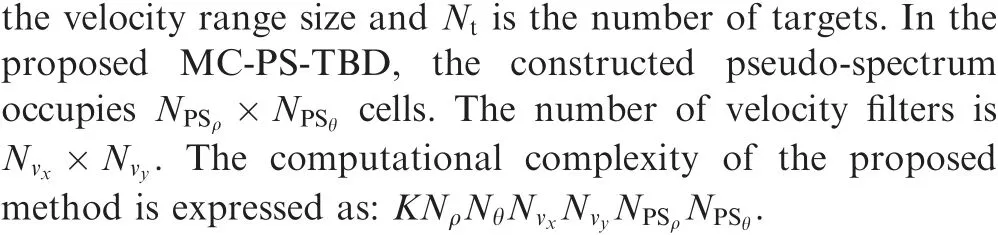
An experimental example is provided for the comparison of computational complexity of DP-TBD and the proposed MCPS-TBD. The number of cells in an observed image is N×N=100×100. The possible velocity range is (-3 cell/frame, 3 cell/frame) in each direction. Then, N=N=7,N×N=31assuming that the filter bank width is 0.2 cell/frame, and N=37assuming that the number of total frames K is 6.

The comparison of computational complexity for different numbers of targets is shown in Fig.6.It can be found that the computational complexity of DP-TBD is influenced by the amount of targets in the observation area. Compared with DP-TBD, the complexity of the proposed MC-PS-TBD does not depend on the number of targets. This contributes to track-before-detect in scenarios with plenty of targets. In the case of N=N=1,the integration strategy in the proposed method degenerates to the cell-to-cell integration strategy in the traditional VF-TBD algorithms.

4. Simulation results

In this section, simulations are conducted to verify the performance of the proposed method.The detection probability Pis defined as the probability that the declared target is within 2 cells from the actual one. The threshold is chosen at a false

4.1. Performance verification with velocity mismatch errors

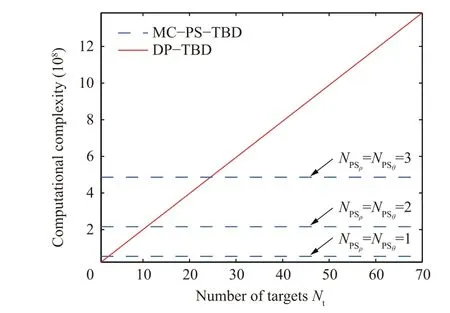
Fig. 6 Comparison between computational costs of DP-TBD and the proposed MC-PS-TBD method.

This subsection devotes to the performance verification of the proposed MC-PS-TBD in the presence of velocity mismatch errors. The initial target state is set as (10 km, -100 m/s,15 km,100 m/s).Fig.7 shows the performance of the proposed MC-PS-TBD with different velocity mismatch errors Δv cell/frame over 6 frames.According to Eq.(46)or Fig.2,the filter bank width approximately equals 0.2 cell/frame, and the mismatch error cannot be larger than half the filter bank width.As illustrated in Fig. 7, the performance of the proposed MC-PS-TBD is degraded slightly as the mismatch error increases. This performance degradation is acceptable and expected since velocity mismatch has negative influence on energy integration. To match the target velocity better and mitigate the above performance degradation, the filter bank width can be reduced, but at the cost of increasing computational complexity as discussed in Section 3.4.2.

4.2. Performance comparison in single-target scenario

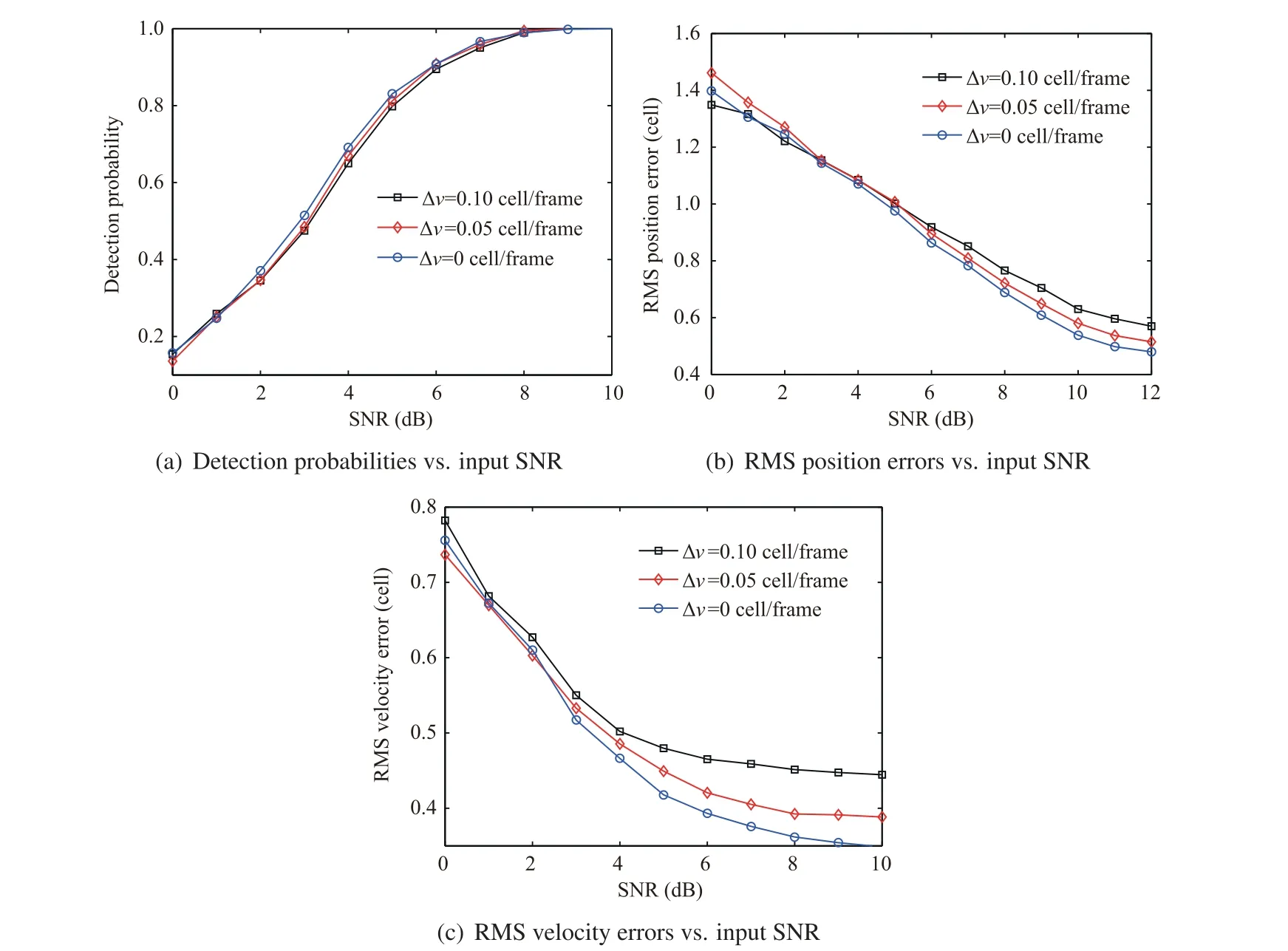
Fig. 7 Performance verification of the proposed MC-PS-TBD with different velocity mismatch errors Δv cell/frame over 6 frames.

In this subsection, targets in the far and near fields of sensor are dealt with respectively. The corresponding initial positions of the targets in Cartesian coordinates are (350 km, 300 km)and (25 km, 20 km), respectively. The targets are assumed to have constant Cartesian velocities of v=-100 m/s and v=100 m/s in each direction. The range resolution Δof the sensor equals 1 km while the angle resolution Δis 1°.Amplitude based DP-TBD (A-DP-TBD) and log likelihood ratio based DP-TBD(LLR-DP-TBD)in Refs.[13,16]are used to compare with the proposed MC-PS-TBD.

4.2.1. Detection probability comparison

The detection probabilities Pof the proposed MC-PS-TBD are compared with those of DP-TBD methods in this subsection. Figs. 8 and 9 show the detection probabilities under different input SNR values and numbers of frames in the far and near fields of sensor, respectively.

As illustrated in Figs. 8 and 9, MC-PS-TBD exhibits superior detection performance than DP-TBD. DP-TBD methods perform energy integration by searching for the maximum value in the feasible transition region of the target.In the case of low SNR, the intensity of noise may often be larger than that of target-originated returns and the DP-TBD may achieve inaccurate target energy integration.On the contrary,the proposed MC-PS-TBD integrates the target energy along its track by matching the Cartesian velocity. The target echo can be integrated correctly, while noise intensity is accumulated slowly due to its independence.

In addition,as shown in Figs.8(a)and 9(a),when the target is near the sensor, the detection performance of DP-TBD drops, while that of MC-PS-TBD does not. In DP-TBD, the inaccurate motion approximation in sensor coordinates may cause model mismatch and integrated energy loss.This performance degradation is significant in near-field scenarios.On the contrary, the proposed MC-PS-TBD can eliminate the model mismatch through the accurate target position prediction in mixed coordinates. This contributes to accurate target energy integration and reliable target detection. The above result can also be observed in Figs. 8(b) and 9(b).

4.2.2. RMSE comparison

The RMSE values of parameter estimates of MC-PS-TBD and DP-TBD methods are compared in this subsection. Figs. 10 and 11 show the RMS position errors under different numbers of frames and SNR values in the far and near fields of sensor,respectively.

Figs.10 and 11 show that the proposed MC-PS-TBD yields better estimates than DP-TBD. As discussed above, the integration strategy in DP-TBD may result in invalid energy integration along an inaccurate trajectory, resulting in large estimation errors. In contrast, the echo energy of target can be accumulated correctly along the target trajectory by matching the actual target velocity in the proposed MC-PS-TBD.Due to the pseudo-spectrum based integration,the target integrated envelope is maintained well and the parameters can be estimated according to the characteristics of integrated envelopes. This contributes to better estimation performance by the proposed MC-PS-TBD.

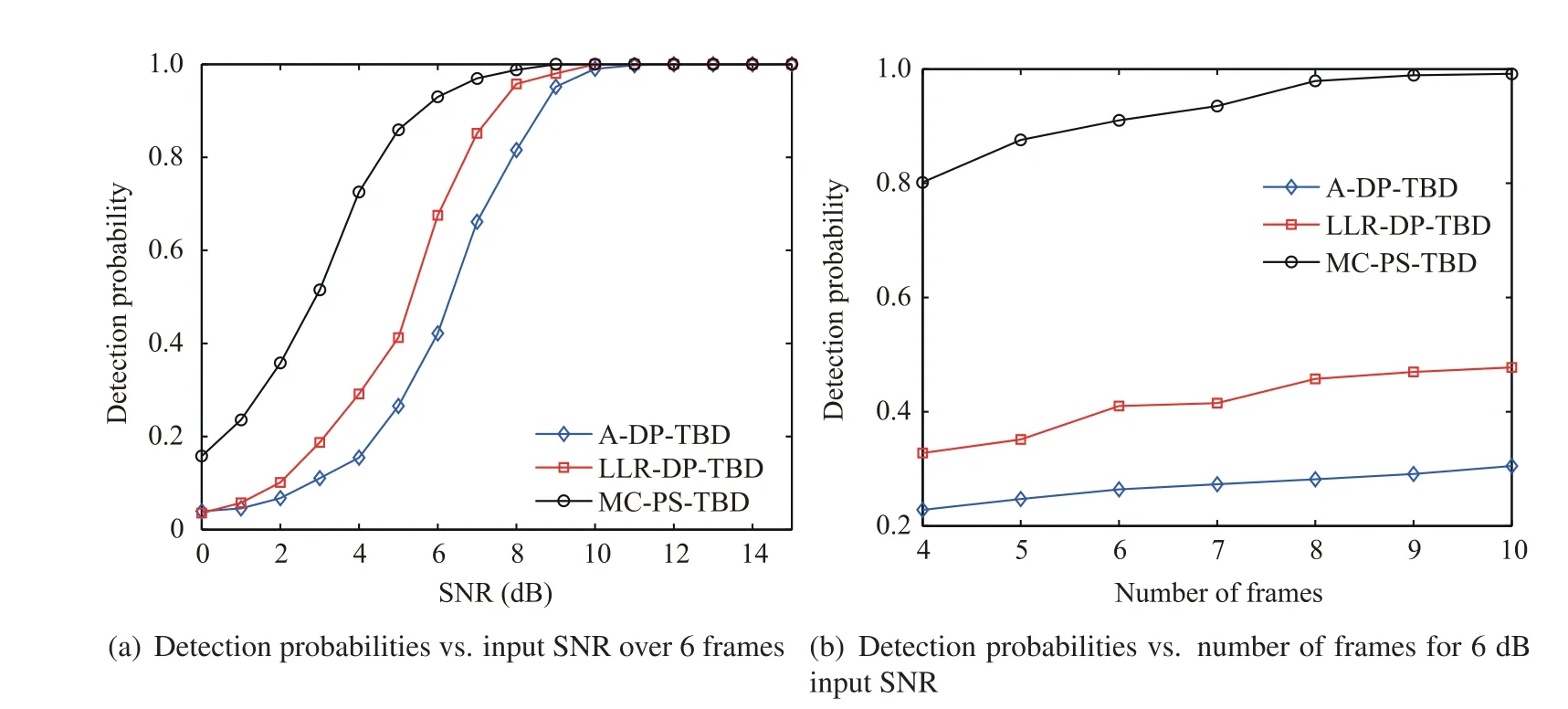
Fig. 8 Comparison of detection probabilities in far-field scenario.

As illustrated in Figs.10(b)and 11(b),the estimation accuracy of DP-TBD can not be improved by increasing the number of integration frames. It is reasonable since the inaccurate integration will still persist in each frame when the noise intensity is larger than the target echo intensity. Conversely,due to the accurate integration of target echo energy in the proposed MC-PS-TBD, with more frames in the processing batch, the target energy can be accumulated better,resulting in improved parameter estimation.

In addition, as shown in Figs. 10 and 11, the estimation accuracy of DP-TBD drops when the target is close to the sensor, but that of MC-PS-TBD does not. This results from the inaccurate energy integration using approximate models in DP-TBD.

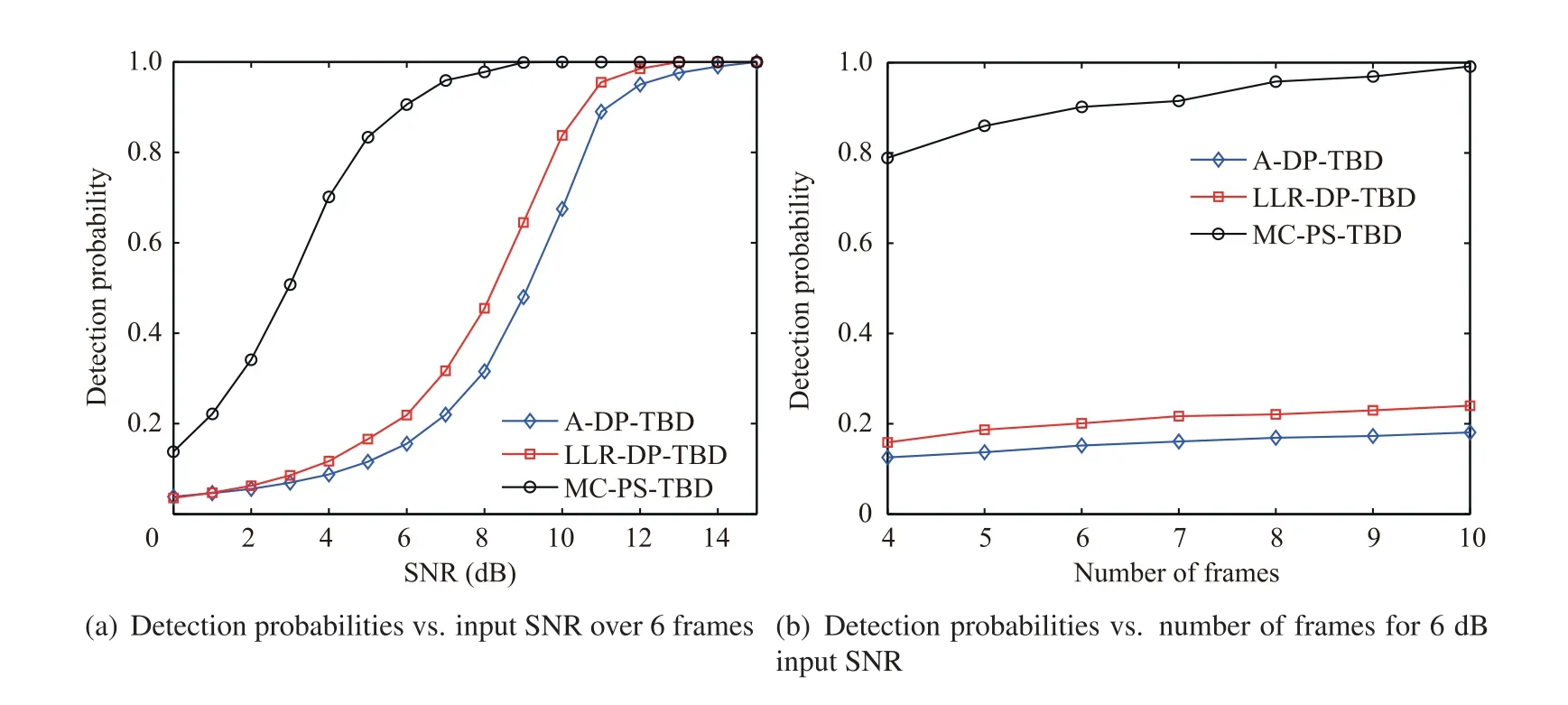
Fig. 9 Comparison of detection probabilities in near-field scenario.

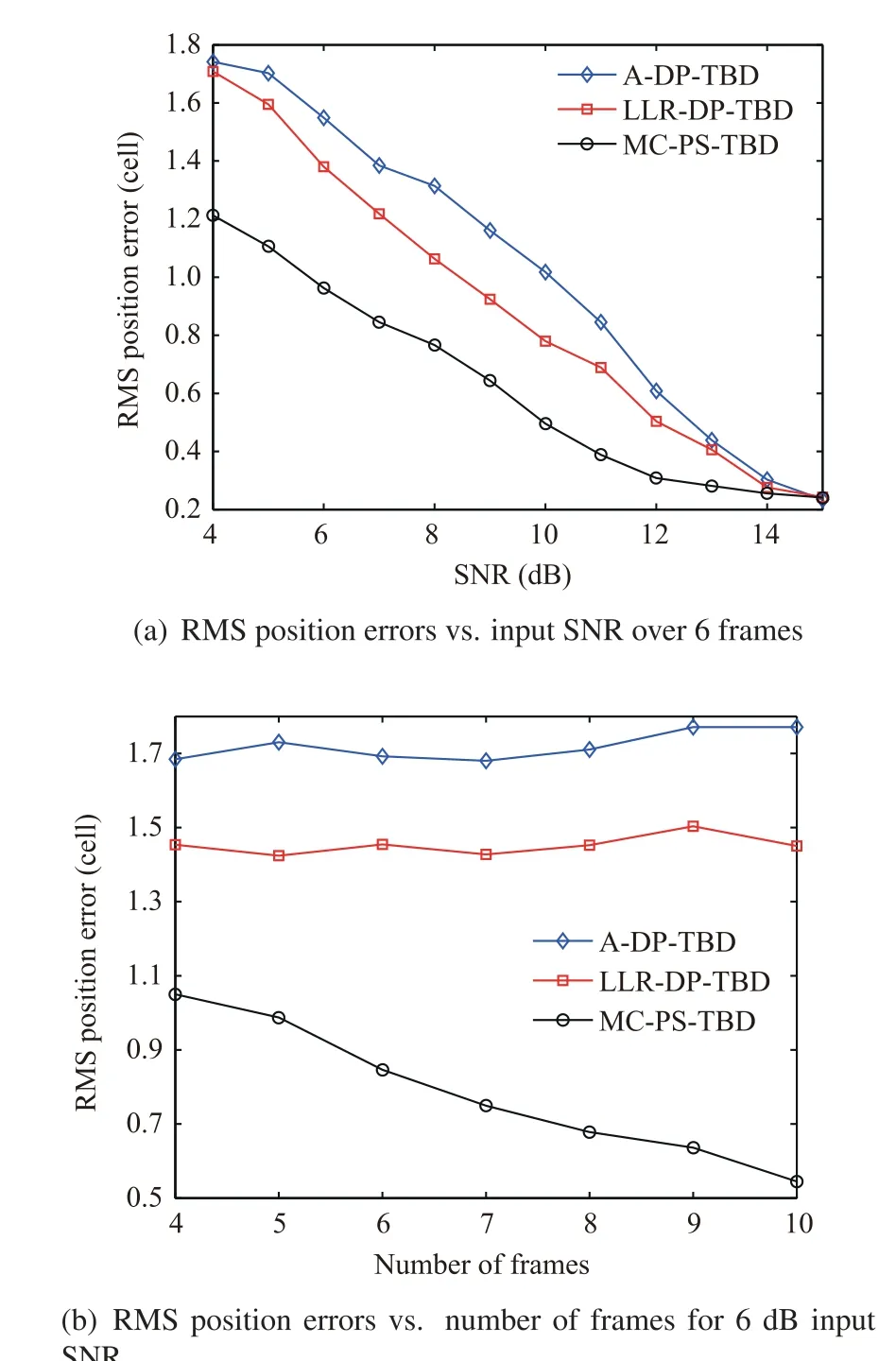
Fig. 10 Comparison of RMS position errors in far-field scenario.

Fig. 12 plots the RMS velocity estimation errors against number of frames and input SNR. The proposed MC-PSTBD can produce accurate velocity estimates while DP-TBD cannot. As illustrated in this figure, the velocity estimation accuracy of a target close to the sensor is better than that of a target far from the sensor.As derived above,the envelope in velocity domain broadens when the target is in the far field of sensor. That is, velocity resolution property of the proposed method becomes worse when the target is away from the sensor, resulting in larger velocity estimation errors.

4.2.3. Performance comparison in the presence of process noise

Since LLR-DP-TBD can obtain better performance than ADP-TBD, only LLR-DP-TBD is used here to compare with the proposed MC-PS-TBD in the presence of process noise.The initial target state is (75 km, -100 m/s, 50 km, 100 m/s),and the process noise is Gaussian distributed with zero mean and standard deviation σm/s.

Fig. 13 shows the performance comparison between LLRDP-TBD and the proposed method in the presence of process noise.The performance of the proposed method is better than that of LLR-DP-TBD due to the use of accurate model as discussed above.However,as illustrated in this figure,the performance of MC-PS-TBD is degraded with increasing standard deviation of process noise. This is expected since the motion uncertainty has negative influence on the target position prediction, but the performance degradation can be ignored in case of small process noise.

In comparison, DP-TBD methods have the advantage of dealing with targets with motion uncertainty or weak maneuver, but suffers from target output envelope expansion. The proposed velocity matched filtering based approach has the strength of high multiframe integration efficiency and well target envelope maintenance, which is beneficial to target detection and parameter estimation. But its performance may be degraded in the case of model mismatch.

4.3. Performance comparison in multi-target scenario

In this subsection, a multi-target scenario is designed to verify the performance of the proposed MC-PS-TBD. Five targets move in the observation region of sensor,and Fig.14(a)shows the trajectories of these five targets in polar coordinates. As illustrated in this figure, targets 1 and 2 are a pair of crossing targets,targets 3 and 4 move almost in parallel,and target 5 is an isolated target far from others. The range resolution Δof the sensor equals 1 km while the angle resolution Δis 2° in this subsection. For comparison, DP-TBD for multi-target processing (MT-DP-TBD)is also considered here.

4.3.1. Detection probability comparison

Fig. 14(b) illustrates the detection probabilities of all five targets with DP-TBD and the proposed MC-PS-TBD over different input SNR values, respectively. As expected, the detection probabilities of all five targets approach 1 as the input SNR increases.

As illustrated in Fig. 14(b), the detection probabilities of five targets in MC-PS-TBD are all larger than the corresponding values in DP-TBD.As discussed above,the accurate target echo energy integration in sensor coordinates is the key reason for the target detectability improvement in the proposed MCPS-TBD.

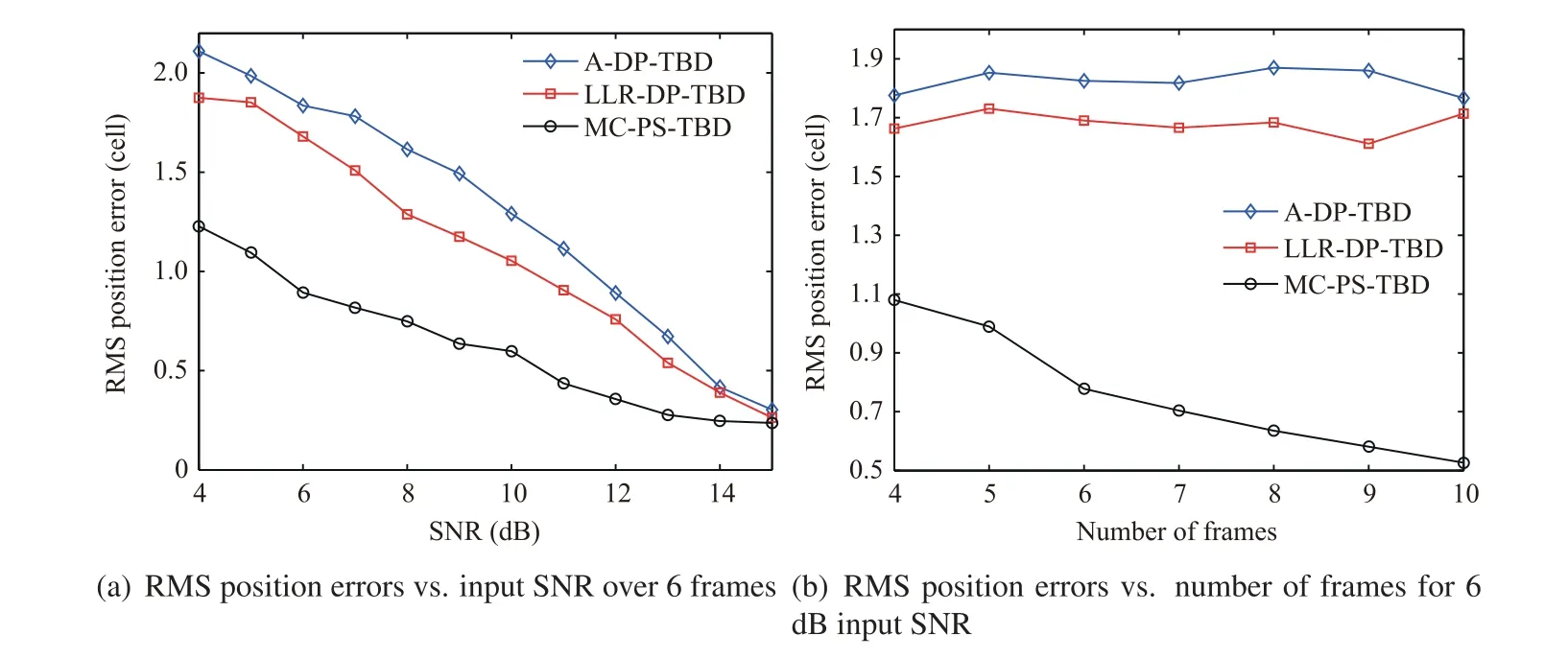
Fig. 11 Comparison of RMS position errors in near-field scenario.

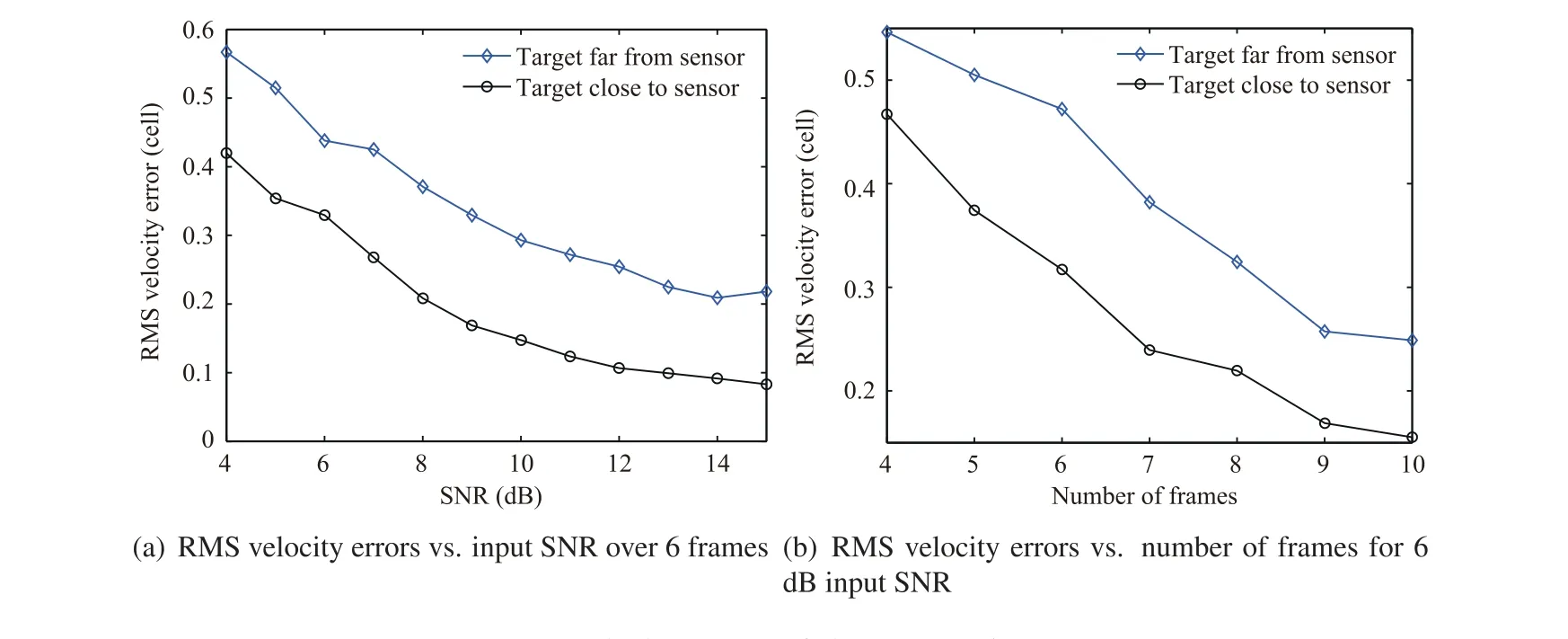
Fig. 12 RMS velocity errors of the proposed MC-PS-TBD.

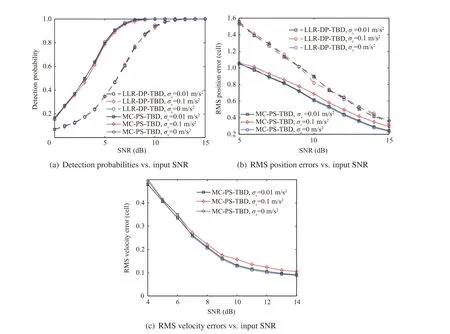
Fig. 13 Performance comparison in the presence of process noise with different standard deviations σv.

The detection probabilities of the two crossing targets (i.e.,targets 1 and 2)with MC-PS-TBD and DP-TBD are both low.This is because the crossing targets may interfere with each other. Compared with DP-TBD, the proposed method can obtain better performance in crossing target detection by handling targets 1 and 2 in different filters with different assumed velocities. This mitigates the effect of target interference.

In addition,the target interference is also the reason for the performance degradation of the targets moving in parallel(i.e.,targets 3 and 4). The detection performance in DP-TBD degrades more than that of MC-PS-TBD.The suboptimal target energy integration in DP-TBD may lead to an extended integrated envelope, impacting the detection of adjacent targets. On the contrary, the integrated envelope in MC-PSTBD is focused better. The integrated envelope extension has been discussed in Section 3.6.1.

4.3.2. RMSE comparison

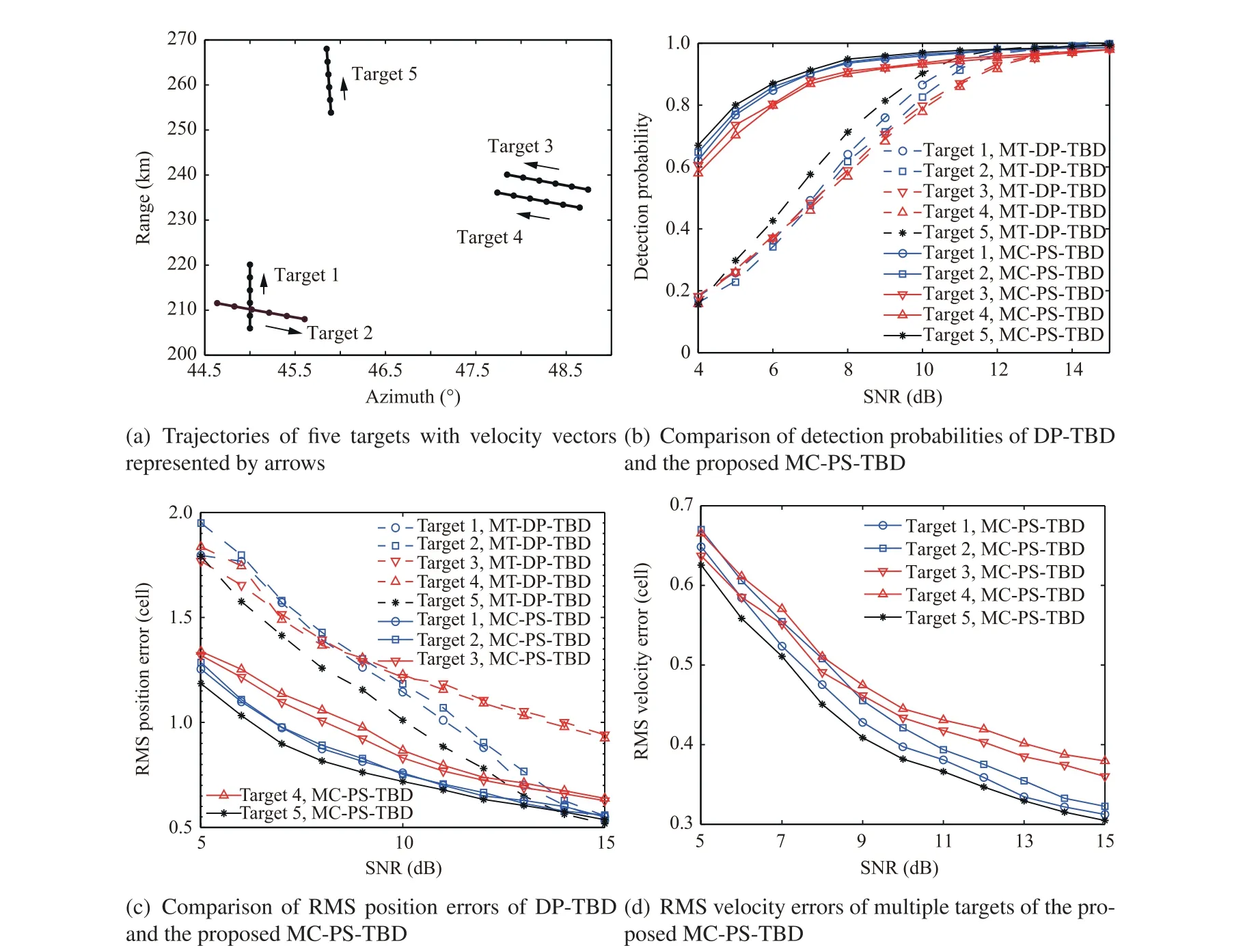
Fig. 14 Performance comparison in multi-target scenario.

Fig. 14(c) shows the RMS position errors of five targets with DP-TBD and the proposed MC-PS-TBD for different input SNR values, respectively. Compared with those of the proposed method,the estimation errors of DP-TBD are worse due to suboptimal energy integration.The estimation accuracies of adjacent targets with the proposed MC-PS-TBD are better than those obtained with DP-TBD. The velocity estimation errors of five targets obtained with MC-PS-TBD are shown in Fig. 14(d).

5. Conclusions

In this paper, a new multiframe TBD method based on pseudo-spectrum in mixed coordinates was proposed to detect and track weak targets in range-azimuth plane effectively.The target position was predicted accurately in Cartesian coordinates, and then the pseudo-spectrum was constructed in polar coordinates for multiframe integration. This avoided the inaccurate energy integration that may result from motion model mismatch in sensor coordinates. The well-maintained integrated envelope facilitated improved parameter estimation using envelope characteristics. The detailed multiframe accumulation procedure and integrated envelope were derived for the proposed pseudo-spectrum approach in mixed coordinates.To cope with the unknown target Cartesian velocity,a velocity filter bank based on pseudo-spectrum in mixed coordinates was proposed. The impact of velocity mismatch on the algorithm performance was investigated. An efficient method was presented to design the filter bank. Precise parameter estimation using characteristics of integrated envelope was presented.Theoretical analysis and simulation results showed the advantages of the proposed MC-PS-TBD over existing MF-TBD methods in terms of envelope maintenance, computational complexity, detection probability, estimation accuracy and multi-target processing.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgement

This work was supported by the National Natural Science Foundation of China (No. 61671181).

Appendix A. In the appendix, the approximation of target envelope in the velocity domain in Eq.(36)is derived in detail.Expanding fin Eq. (31) as a Taylor series, the target integrated envelope in Eq. (30) can be rewritten as

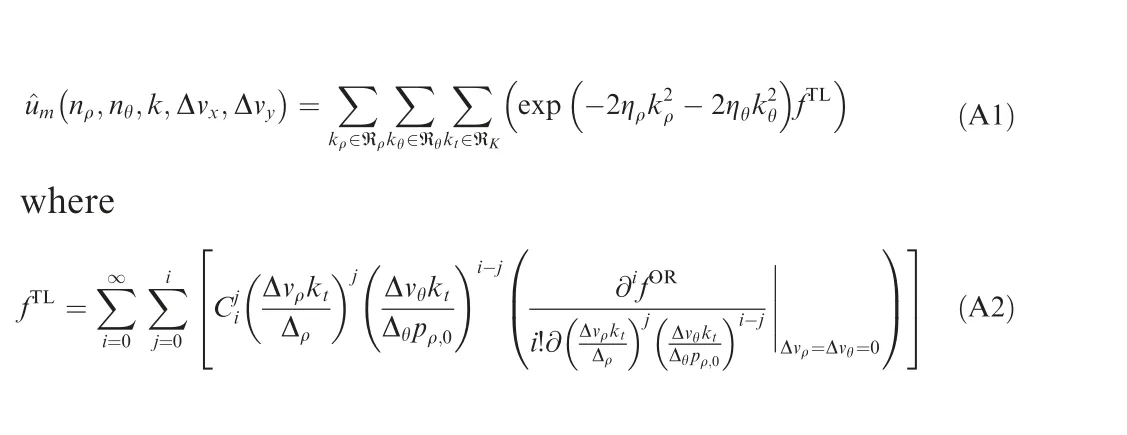
where Q，Q，Q，q，q，qand qare coefficients expressed in Section 3.4.2, respectively.