De-combination of belief function based on optimization

Xiojing FAN, Deqing HAN,*, Yi YANG, Jen DEZERT

a School of Automation Science and Engineering, Xi’an Jiaotong University, Xi’an 710049, China

b SKLSVMS, School of Aerospace, Xi’an Jiaotong University, Xi’an 710049, China

c ONERA, The French Aerospace Lab, Palaiseau 91761, France

KEYWORDS Belief functions;De-combination;Divergence maximization;Information fusion;Information maximization

Abstract In the theory of belief functions, the evidence combination is a kind of decision-level information fusion.Given two or more Basic Belief Assignments (BBAs) originated from different information sources, the combination rule is used to combine them to expect a better decision result.When only a combined BBA is given and original BBAs are discarded, if one wants to analyze the difference between the information sources, evidence de-combination is needed to determine the original BBAs. Evidence de-combination can be considered as the inverse process of the information fusion. This paper focuses on such a defusion of information in the theory of belief functions. It is an under-determined problem if only the combined BBA is available. In this paper,two optimization-based approaches are proposed to de-combine a given BBA according to the criteria of divergence maximization and information maximization, respectively. The new proposed approaches can be used for two or more information sources. Some numerical examples and an example of application are provided to illustrate and validate our approaches.

1. Introduction

The theory of belief functions,also called Dempster-Shafer Theory (DST), is a powerful tool for uncertainty modeling and reasoning.It has been used in a wide range of applications such as multi-sensor data fusion,multiple criteria decision making,pattern classification,image processing,and so on.In belief functions, evidence combination is an important and typical information fusion. Many combination rules have been proposed,such as Dempster’s rule of combination,Yager’s rule,Dubois & Prade’s rule,Smets’rule,Murphy’s rule,Florea’s rule,and two combination rules using Proportional Conflict Redistribution(PCR5 and PCR6).

The inverse process of evidence combination can be called‘‘evidence de-combination”, which was first proposed by Smets.Based on the canonical decomposition of a belief function, he defined the de-combination operator for a belief function. In belief functions, little research has been carried out on the evidence de-combination, especially when all original evidences are unknown.The term of‘‘de-combination”can be regarded as the inverse process of the information fusion,which can also be called as information‘‘defusion”.It is meaningful in information processing and analysis. When only the combined BBA is available and the original BBAs are discarded, to analyze the difference between the information sources, the original BBA of each information source is needed.The original BBAs to combine can be obtained by evidence de-combination. Besides, one can evaluate different combination rules by using the evidence de-combination. If a combination rule used to construct the de-combination can bring out a more divergent BBA pair compared with other rules, this rule can aggregate (combine) a more divergent BBA pair to the same BBA and has a stronger aggregation capability.

Like the Blind Source Separation (BSS),original signals without observations can be determined from multiple observed mixed signals. In BSS, Independent Component Analysis (ICA)is usually used. In the case that the original signals and signal mixing method are unknown, the observed mixed signals are expressed as linear combinations of statistical independent component variables, which are used as approximate estimations of the original signals. We try to de-combine a given BBA under the framework of belief functions in this paper, which is similar to the BSS in signal processing. For simplicity, our research is to start with the evidence de-combination for two information sources. It is found through analysis that given the combined BBA and one of original BBAs at the same time, the evidence decombination is a well-posed problem. That is to say,the other original BBA can be uniquely determined.When both original BBAs are unknown and only the combined BBA is given, it is an under-determined problem, i.e., with multiple solutions.How to deal with the under-determined problem in the evidence de-combination? Inspired by BSS, we attempt to solve an optimization problem to de-combine a given BBA. The known combined BBA can be regarded as the observed mixed signal in BSS, while the original BBAs to determine are regarded as the original signals without observations in BSS.In BSS, Minimum Mutual Information (MMI)can implement blind signal separation based on the criterion of the maximization of difference between information sources. The distance of evidence represents the degree of dissimilarity between BBAs in the theory of belief functions. Therefore,we use for reference the criterion in MMI to construct a maximization problem to determine the original BBAs, where the distance of evidence between original BBAs are used to construct the objective function. Furthermore, infomax algorithmin BSS can implement blind signal separation based on the maximization of entropy of the separation system. In the theory of belief functions, the uncertainty measure can describe or measure information content in a BBA.Therefore,we also use for reference infomax algorithm to construct a maximization problem to determine the original BBAs, where the objective function is established based on the uncertainty measures of original BBAs.

In summary, we propose two evidence de-combination methods based on two different maximization problems,respectively. According to the combination rule used and the legitimacy conditions of original BBAs, the constraints for the maximization are constructed. Examples are provided to verify our methods for the evidence de-combination. Furthermore,we extend the evidence de-combination for two information sources to that for more than two information sources by solving the optimization problem.In addition,from the application aspect, the evidence de-combination method that uses the evidence distance is used to evaluate the aggregation capability of different combination rules. The larger the distance between the original BBAs obtained,the stronger the aggregation capability of the corresponding rule. An example is provided to show that the aggregation capabilities of four combination rules are different and the order of the aggregation capabilities of four rules in a statistical sense is given.

The work in this paper is an extension of our preliminary work presented.The added values include the following. In addition to the evidence de-combination method based on the maximization of the evidence distance between two original BBAs to determine, a method based on the maximization of the difference between the uncertainty of original BBAs to determine is also proposed. Furthermore, more different evidence distance measures and uncertainty measures are used to construct the objective functions of the maximization problems in this paper.We also use the evidence de-combination to deal with the situation where there are more than two information sources and obtain three or four original BBAs. To illustrate how to use the evidence de-combination to evaluate the aggregation capability of different combination rules, an example is provided.

This paper is organized as follows. In Section 2, we introduce the basics for theory of belief functions. In Section 3,two methods of the evidence de-combination for two information sources are proposed. Some analyses on the evidence decombination are provided and the evidence de-combination for three or more information sources are proposed in Section 4. In Section 5, some numerical examples and analyses are provided. In Section 6, we introduce some applications of the evidence de-combination including the aggregation capability evaluation of different combination rules. Section 7 concludes this paper.

2. Preliminary

2.1. Basics of theory of belief functions

The classical belief functions theory is defined under the closed-world assumption. In addition, under the open-world assumption, the mass assignment of the empty set is nonzero.See more details in the work of Smets and Kennes.

In general, Dempster’s rule of combination can be considered as a multiplicative and conjunctive fusion rule.It has been criticized for its counter-intuitive behavior, especially if high conflict between BBAs exists.To overcome limitations of Dempster’s rule, various alternative combination rules2have been proposed.

For Yager’s rule, the conflict between BBAs represents the unknown information, which is the most ambiguous and should be assigned to the complete set.Two BBAs mand mcan be combined using Yager’s rule defined by

2.2. Distance of evidence

2.3. Uncertainty measure of BBA

3. Evidence de-combination in belief functions theory

The information fusion in the theory of belief functions is usually implemented by the operations like evidence updatingor evidence combination. Evidence updating is the revision or focus of the original BBA. See more details in Ref. 54. Evidence combination can be considered as a procedure shown in Fig.1,where mand mare two BBAs defined on the same FOD. mand mcan be combined using combination rule.Then, the combined BBA m can be obtained.

The evidence de-combination can be considered as a procedure of information defusion as shown in Fig.2.That is to say,given a BBA m obtained after the combination,one can try to obtain the possible original BBAs (mand m).

When only the combined BBA is available,the evidence decombination is required for analyzing the original information sources and judge the relationship between them.For simplicity, we first focus on the evidence de-combination for two information sources. That is, let’s assume that there are only two original BBAs.

3.1. Relation between combined BBA and original ones according to Dempster’s rule

Fig. 1 Evidence combination.

The evidence de-combination for two information sources has two cases. For the first case, the combined BBA m and one of original BBAs are available. The remaining original BBA is unknown.For the BBA to determine,e.g.,m,we have 2simultaneous equations (Eq. (15) and the second equation of Eq. (16)) to determine 2-1 unknown variables. That is,2>2-1.The quantity of the unknown variables is less than that of simultaneous equations. Therefore, it is an overdetermined problem and mcan be determined uniquely. For convenience,this case is represented by‘‘Case I”in the sequel.

In another case, only the combined BBA m is known and both original BBAs (mand m) are unknown. There are（2-1）×2=2-2 unknown variables to determine,while there are only 2-1+2=2+1 equations according to Eqs.(15)-(16). The quantity of the unknown variables is greater than that of simultaneous equations, i.e., 2-2>2+1（n>1）. Therefore, it is an under-determined problem with multiple solutions. In the sequel, this case is represented by‘‘Case II” for convenience.

Inspired by BSS, we use optimization-based approach to deal with Case II. The constraints for the optimization-based approach can use the simultaneous equations (i.e., Eqs. (15)-(16)) and the other legitimacy conditions for BBAs to determine (inequality to assure a BBA with the mass value lies in[0,1]). The key issue is to select an appropriate criterion to establish the objective function for the optimization. The evidence de-combination is like the Blind Source Separation(BSS), and we use for reference the ideas in algorithm of BSS to establish the objective function.

3.2. Distance maximization based evidence de-combination

Minimum Mutual Information (MMI)is an algorithm for BSS, where the divergence between different sources is used for the mutual information minimization. The largest divergence represents the minimization of mutual information.Then, we use for reference the criterion in MMI to design the objective function in optimization-based evidence decombination,where the distance of evidence is used to describe the divergence between BBAs.

The distance maximization based evidence de-combination is illustrated in Eq.(17)and Eq.(18),where we use Jousselme’s distanceand the belief interval based distanceas the objective function, respectively. As aforementioned, Eqs. (15)-(16)and inequalities of the mass value range for original BBAs are used to establish the constraints.

Fig. 2 Evidence de-combination.

3.3. Uncertainty difference maximization based evidence decombination

3.4. Illustrative example

With Dempster’s rule,one can obtain a BBA m after the combination of mand m:

There are 2-1+2=9 equality constraints and 14 inequality constraints. According to Eqs. (17)-(20), one can establish the objective function of each of optimization-based evidence de-combination. Then, the BBA pairs can be obtained by using different methods of evidence decombination and are listed in Table 1.

It is easy to verify that m⊕m=m.

4. Further analysis on evidence de-combination

4.1. Optimization criterion selection

Distance maximization and uncertainty difference maximization are adopted in the evidence de-combination, respectively.They are inspired by the minimization of mutual information(i.e., the maximization of divergence) between sources in BSS and maximization of information for the separation system,respectively.

For the evidence de-combination where the objective function is distance,one can also try to implement the evidence decombination based on the distance minimization. Then, we find that the minimum distance might be zero and the obtained BBAs of two sources are identical.

Suppose that the combined BBA is

One can easily verify that m⊕m=m. It is possible for two different and independent sources to provide two identical BBAs. Note that the BBAs provided by different sources are usually different in general. Therefore, we prefer the criterion of distance maximization, which can bring out more distinct evidences.

4.2. Evidence de-combination for more than two information sources

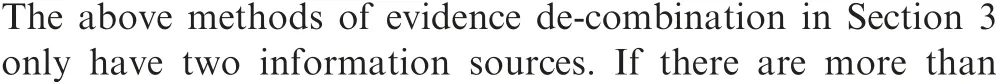
where R（·）can be replaced with different alternative combination rules that satisfy the associative law.

Similarly, using dto construct the objective function, we determine three original BBAs by solving the following maximization optimization problem:

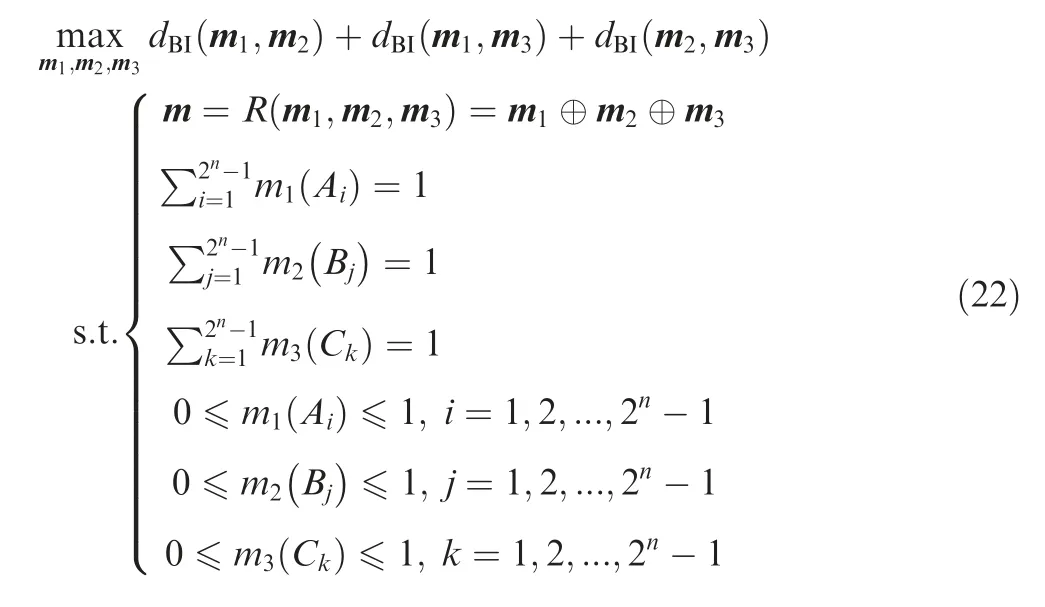
For a given BBA, we can also determine three original BBAs by using EDand ED.When AM(Eq.(11))is used to construct the objective function, the evidence decombination is implemented by solving the following maximization optimization problem:

Table 1 Original BBAs obtained in illustrative example.

The objective function for EDis

Note that the combination rule used to construct the evidence de-combination for more than two sources should satisfy the associative law. This is because the order of the combination for the BBAs obtained by the evidence de-combination is not specified. As mentioned in Section 3, other combination rules can also be used. For the evidence de-combination for two sources, many combination rules can be used, such as Dempster’s rule, Yager’s rule and PCR6. However, if we use the de-combination constructed by the combination rule that does not satisfy the associative law to de-combine a given BBA into more than two BBAs and then we combine these obtained BBAs after changing the combination order,the new combination result might be different from the given BBA.Therefore,if one wants to de-combine a given BBA into more than two BBAs, the combination rule used to construct the evidence de-combination should satisfy the associative law.

5. Examples of evidence de-combination

In this section, we provide some examples to illustrate how to de-combine a given BBA based on the evidence decombination. These examples are numerical examples, which are provided to verify our methods. We use Dempster’s rule that satisfies the associative law to construct the decombination in all examples.

5.1. Example 1

Suppose that the given combined BBA is the same as that in the illustrative example in Section 3.4.

5.2. Example 2

Using ED, ED, EDand ED, the two original BBAs are listed in Table 2.

We can verify that each BBA pair satisfy m⊕m=m.Using different evidence de-combination methods could obtain different BBA pairs.

5.3. Example 3

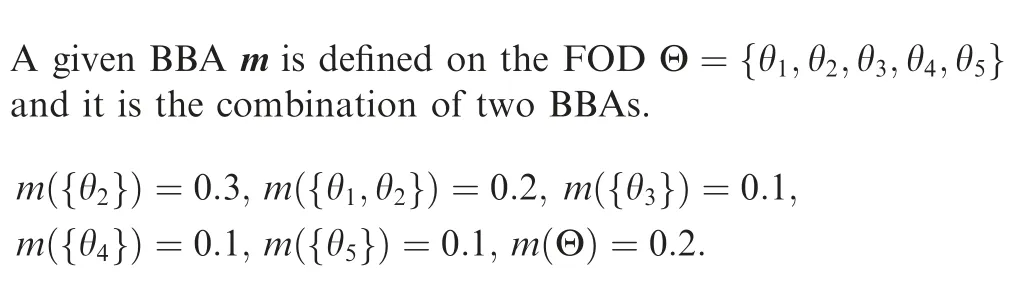
The four BBA pairs respectively obtained by the four evidence de-combination methods are listed in Table 3.

It is easy to verify that all the BBA pairs obtained by the four evidence de-combination methods satisfy m⊕m=m.The BBA pairs obtained by using EDand EDare the same. That is, using different types of evidence decombination might de-combine the same BBA into the same BBA pair.

5.4. Example 4

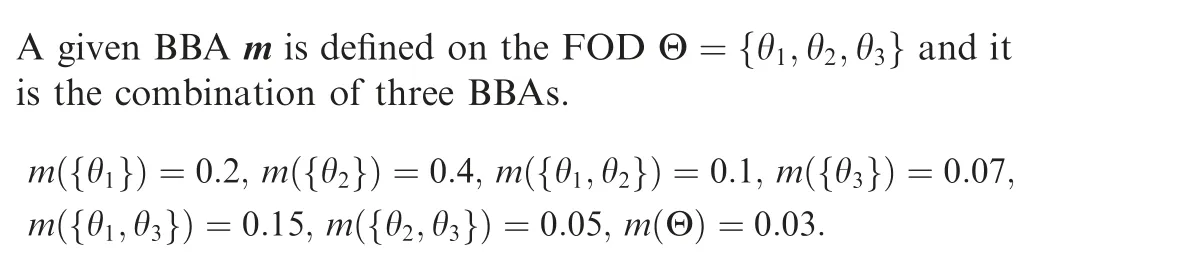
According to ED, ED, EDand ED, the original BBAs are listed in Table 4.

We can verify that m⊕m⊕m=m. According to the results, using different types of distance as the objective function of the distance maximization based evidence decombination can obtain different results. Meanwhile, EDand EDobtain different original BBAs in this example.

5.5. Example 5

According to ED, ED, EDand ED, the BBAs obtained by different evidence de-combination methods are listed in Table 5.

Table 2 Original BBAs obtained in example 2.

Table 3 Original BBAs obtained in example 3.

Table 4 Original BBAs obtained in example 4.

It is easy to verify that m⊕m⊕m=m.According to the results in Table 5,the results obtained by the same type of evidence de-combination have little difference.

5.6. Example 6

5.7. Example 7

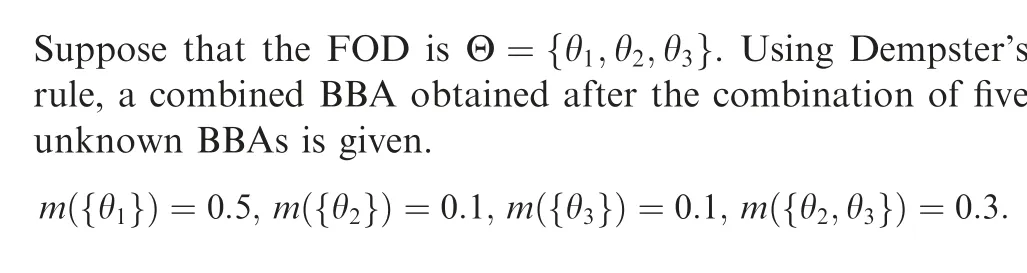
5.8. Example 8

6. Some applications of evidence de-combination

6.1. Evaluation of divergence between sensors

According to a combined BBA m, one can obtain two BBAs mand mafter the evidence de-combination. Suppose that

Table 5 Original BBAs obtained in example 5.

Table 6 Original BBAs obtained in example 6.

Table 7 Original BBAs obtained in example 7.

6.2. Aggregation capability evaluation of combination rule

One can use the evidence de-combination to evaluate different combination rules.In Section 3,we only use Dempster’s rule to construct the evidence de-combination. Besides Dempster’srule, other alternative combination rules can also be used for the evidence de-combination. As mentioned in Section 3,Dempster’s rule used in the first of constraints for the evidence de-combination can be replaced with other alternative combination rules.

Table 8 Original BBAs obtained in example 8.

Given a BBA, different pairs of BBAs can be obtained by using the distance maximization based evidence decombination constructed with different combination rules.Note that the BBA to de-combine is the same one. Then, we calculate the distance between each BBA pair obtained by the evidence de-combination. If a combination rule used to construct the evidence de-combination can bring out a more divergent BBA pair compared with other combination rules,the corresponding rule can combine (aggregate) a more divergent BBA pair to the same BBA. This is to say that this combination rule has a stronger aggregation capability. In other words,the distance between each BBA pair is used to describe the aggregation capability of the combination rule used to construct the de-combination.If the distance between a BBA pair obtained by the evidence de-combination is larger, the aggregation capability of the corresponding combination rule is stronger. Here, an example is provided to illustrate how to evaluate the aggregation capability of different combination rules.

In this example, we compare the aggregation capability of four combination rules including Dempster’s rule of combination (Eq. (4)), Yager’s rule (Eq. (5)), Dubois & Prade’s rule(Eq. (6)), and PCR6 (Eq. (7)). For convenience, these four combination rules are respectively represented by ‘‘R”,‘‘R”, ‘‘R” and ‘‘R”. We evaluate the aggregation capability of the four combination rules through 300-run Monte-Carlo experiments so that the result in a statistical sense of comparative result can be obtained. How to evaluate the aggregation capability of these four combination rules?EDor EDfor two information sources are used to decombine a given BBA into two BBAs. For simplicity, we first assume that the FOD is Θ= ｛θ，θ，θ｝.

On each run, the given combined BBA is taken randomly and four combination rules are respectively used in the evidence de-combination to de-combine the given BBA. Then,we can obtain four BBA pairs by EDor EDand calculate the distance between each BBA pair.The distance between the two BBAs in pair is used to represent the aggregation capability of the corresponding combination rule. The four distances are arranged in descending order, and the ranking of the corresponding rules is recorded.If the distance is larger,the ranking of the corresponding combination rule is higher. In other words, the combination rule corresponding to the largest distance is ranked as‘‘1”and the combination rule corresponding to the smallest distance is ranked as ‘‘4”. Then, we count the cumulative number of the ranking of four combination rules in 300-run experiments, as shown in Table 9 and Table 10 below. The cumulative number of ranking obtained by using EDare listed in Table 9. The cumulative number of ranking obtained by using EDare listed in Table 10.

According to the results in Table 9 and Table 10,the order of the aggregation capability of the four combination rules can be obtained.From the strongest to the weakest,they are R,R, R, R.

In order to bring a more general result of the aggregation capability of different combination rules, different numbersof elements of the FOD are used for another group of 300-run Monte-Carlo experiments. The FOD in every 100-run experiment contains 2,3 and 4 elements,respectively.On each run, the given BBA is also taken randomly. We use EDand EDto de-combine the given BBA into two BBAs, respectively. The following tables list the cumulative number of the ranking of four combination rules. The results of ranking obtained by using EDand EDare listed in Table 11 and Table 12, respectively.

Table 9 Cumulative number of ranking by using EDdJ(Θ= ｛θ1，θ2，θ3｝).

Table 10 Cumulative number of ranking by using EDdBI(Θ= ｛θ1，θ2，θ3｝).

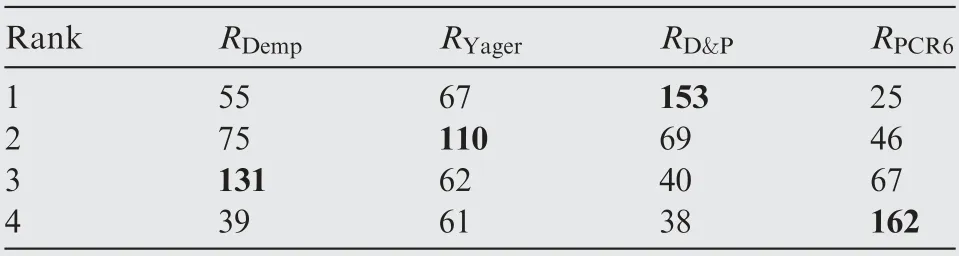
Table 11 Cumulative number of ranking by using EDdJ.

Table 12 Cumulative number of ranking by using EDdBI.

According to Table 11 and Table 12, the descending order of aggregation capability of the four combination rules is R, R, R, R. This is the same as the results in Table 9 and Table 10.

7. Conclusions

In this paper, two methods of evidence de-combination are proposed, where the distance maximization criterion and uncertainty difference maximization criterion are adopted in the evidence de-combination.Different evidence distance measures and uncertainty measures are used to construct the corresponding objective function of different methods,respectively. For two or more information sources, the evidence de-combination can be used to determine original BBAs when only combined BBA is given. Some numerical examples show that all the proposed methods can de-combine a given BBA effectively. Some applications of evidence decombination are given in this paper. For example, using the evidence de-combination, one can evaluate the aggregation capability of different combination rules.

In our future work, we will try to design other types of the evidence de-combination method for more than two sources to simplify the calculation. Considering the prior information about the information sources, we will try to use the evidence de-combination to obtain BBAs which approximate to the actual original BBAs.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

This work was supported by the National Natural Science Foundation of China (No. 61671370), Project supported by joint foundation of X Lab - the 2Academy of CASIC, the PostdoctoralScienceFoundationofChina(No.2016M592790) and the Postdoctoral Science Research Foundation of Shaanxi Province, China (No. 2016BSHEDZZ46).