Mahalanobis distance-based fading cubature Kalman filter with augmented mechanism for hypersonic vehicle INS/CNS autonomous integration

Binging GAO, Wenmin LI, Goge HU, Yongmin ZHONG, Xinhe ZHU

a School of Automation, Northwestern Polytechnical University, Xi’an 710072, China

b School of Engineering, RMIT University, Bundoora, VIC 3083, Australia

KEYWORDS Autonomous integration;Fading factor;Hypersonic vehicle;Inertial navigation systems;Kalman filters;Mahalanobis distance

Abstract Inertial Navigation System/Celestial Navigation System (INS/CNS) integration, especially for the tightly-coupled mode,provides a promising autonomous tactics for Hypersonic Vehicle(HV)in military demands.However,INS/CNS integration is a challenging research task due to its special characteristics such as strong nonlinearity, non-additive noise and dynamic complexity.This paper presents a novel nonlinear filtering method for INS/CNS integration by adopting the emerging Cubature Kalman Filter(CKF)to handle the strong INS error model nonlinearity caused by HV’s high dynamics. It combines the state-augmentation technique into the nonlinear CKF to decrease the negative effect of non-additive noise in inertial measurements. Subsequently, a technique for the detection of dynamic model uncertainty is developed, and the augmented CKF is modified with fading memory to tackle dynamic model uncertainty by rigorously deriving the fading factor via the theory of Mahalanobis distance without artificial empiricism. Simulation results and comparison analysis prove that the proposed method can effectively curb the adverse impacts of non-additive noise and dynamic model uncertainty for inertial measurements, leading to improved performance for HV navigation with tightly-coupled INS/CNS integration.

1. Introduction

Hypersonic Vehicle (HV) has been viewed as a promising and cost-effective means to fulfill the increasing military demands due to its capability of ‘‘prompt global strike”.However,the HV navigation is still a challenging task due to its special characteristics such as strong nonlinearity, fast time-varying dynamics and complex flight environment.Continual advancements in military demands have brought about increasingly stringent requirements for autonomous HV navigation systems.

Inertial Navigation System (INS) is the most popular autonomous navigation method in the recent decades.It is self-contained, operates continuously and provides navigation solutions with low short-term noise. However, it suffers from accuracy degradation with time due to the biases and drifts of the Inertial Measurement Unit (IMU).Thus, INS must be supplemented with other navigation sensors to achieve continuous and accurate navigation solutions. Global Navigation Satellite System (GNSS) is commonly integrated with INS to correct INS navigation error.However, since GNSS is not an autonomous navigation system, its satellite signal is easily disturbed in military applications, leading to discontinuous and poor correction for INS navigation error.Celestial Navigation System (CNS) is also an autonomous navigation technique to provide attitude and position information by observing celestial bodies.It has unparalleled advantages over other navigation systems, such as non-cumulative error quality,strong anti-interference ability and high reliability.Consequently, considering the complementary nature of CNS and INS, integrating CNS with INS is a promising scheme to improve the reliability and autonomy for HV navigation using CNS information to compensate the navigation error of INS.

Similar to INS/GNSS integration, CNS can be integrated with INS in both loosely-coupled and tightly-coupled modes.The former considers vehicle position or attitude information output by CNS as the measurement to correct INS navigation error, while the latter directly uses the raw observation information (elevation angle or azimuth angle)of the target navigation stars to estimate INS navigation error.Compared to the loosely-coupled mode, the tightly-coupled mode avoids computational errors introduced by solving the position and attitude from CNS, and thus it has been widely used in INS/CNS integration.

The existing studies on tightly-coupled INS/CNS integration are mainly dominated by a linear system resulted from the first-order Taylor expansion of the actual nonlinear system,where the data fusion is conducted by the conventional Kalman Filter (KF) or Extended Kalman Filter (EKF) for navigation solutions.The linearization of the dynamic model, i.e, the resultant linear INS error model, is based on the assumption that the initial state estimate involves small error to reduce the computational cost. Nevertheless, in most practical applications, since the true initial state is unknown,it is difficult to satisfy this assumption, especially for highly dynamic vehicles such as HV. Further, the raw observation information (elevation angle or azimuth angle) of the target navigation stars is directly used in the system measurement model, leading to strongly nonlinear characteristics.Due to the above reasons, the use of the conventional KF or EKF in tightly-coupled INS/CNS integration suffers from poor estimation accuracy for HV navigation.

Both Unscented Kalman Filter (UKF) and Particle Filter(PF)are the nonlinear estimation methods for strongly nonlinear systems.UKF uses deterministic sigma points to capture higher-order statistics of the system, avoiding the system model linearization. Despite its higher filtering accuracy and convergence than EKF,UKF has a stability issue due to the occurrence of negative weights on sigma points, especially for high-dimensional (more than 3) nonlinear systems such as tightly-coupled INS/CNS integration.PF is based on Monte Carlo simulation to approximate the posterior distribution of system state with a large number of particles.However,the large number of particles used in the resampling process leads to an expensive computational load, making it difficult to be used in practical high-dimensional navigation systems.

Cubature Kalman Filter (CKF) is a relatively new nonlinear filtering strategy for high-dimensional state estimation,which was proposed to overcome the limitations of EKF and UKF.It approximates the numerical integration on a Bayesian posterior probability density function using spherical-radial cubature rule, resulting in at least secondorder Taylor accuracy for the state posterior mean and covariance. Thus, CKF has improved numerical stability and accuracy compared to EKF and UKF for high-dimensional systems. Further, CKF also has less computational burden than UKF, since it contains 2n cubature points while UKF contains 2n+1 sigma points.However,since the conventional CKF is originally derived under the assumption of additive noise, if the nonlinear INS error model has non-additive noise properties, the performance of the conventional CKF will be degraded.Furthermore, the implementation of CKF requires the system model to be pre-defined exactly. If the system model involves uncertainty,the CKF filtering accuracy will also be deteriorated.However,it is impossible to acquire the actual noise and error of real HV flight to establish exact system model for the tightly-coupled INS/CNS integration due to the highly dynamic flight and complex flight environment.With advanced star sensor technologies, the high accuracy of the measurement model can be guaranteed using highly accurate measurement devices or a large amount of redundant observation data by multiple navigation stars.Nevertheless, the dynamic model used in the HV navigation is only a theoretical approximation to the real-world system, inevitably involving error. Moreover, in highly dynamic flight,the actual dynamic noise of HV navigation is always non-Gaussian.However, in theory, the navigation system’s noise is generally assumed as a Gaussian distribution to simplify the modelling complexity, which also causes dynamic model uncertainty.Accordingly,it is necessary to handle the influence of the noise and error between the dynamic model and actual system on the filtering solution for HV’s accurate navigation and positioning.

Research efforts have been dedicated to handling dynamic model uncertainty to improve the adaptability of the conventional CKF.Generally,dynamic model uncertainty can be further classified into function model uncertainty and stochastic model uncertainty. The former is due to sudden variations of parameters or unknown state biases; while the latter is caused by inaccurate dynamic noise statistics. Both function and stochastic model uncertainties can be handled using various adaptive filters, in which the filtering estimation is recursively tuned according to actual measurements to alleviate the influence of dynamic model uncertainty. Based on the principle of interacting multiple model, Li and Jia developed a modified CKF to enhance the adaptability for mobile station positioning.However, this method results in a large computational burden caused by multiple filters.Cui et al.established an iterative CKF by merging the Sage-Husa noise statistics estimation into CKF to handle dynamic noise uncertainty.However,this method faces the ‘‘rank deficient”issue in noise statistics estimation for high-dimensional systems.In addition,the forgetting factors used in the filter are also determined based on empiricism for the case of time-varying noise statistics.

Apart from the above adaptive filters,fading filters are also widely studied owing to their effectiveness and moderate computational load.On the prerequisite that actual measurement can be correctly achieved, this method constructs a fading factor based on the innovation information to make historical information less weighted and consequently the measurement more weighted to recursively tune the filtering process to mitigate the effect of dynamic model uncertainty.Soken and Hajiyev proposed an adaptive fading UKF to cope with dynamic model uncertainty for satellite attitude estimation.However,similar to the existing fading filters,the determination of the fading factor in this method is also heavily dependent on artificial empiricism.Moreover,the existing fading filters are mainly established based on the conventional Kalman filtering framework with additive noise. There have been limited studies on fading filter for a nonlinear system involving non-additive noise and dynamic model uncertainty,such as the tightly-coupled INS/CNS integration for HV navigation.

Mahalanobis distance is a statistical measure which is widely used to detect the anomaly of multivariate data.Under the Gaussian assumption, the square of the Mahalanobis distance of the filter’s innovation vector, which is defined as the judging index,obeys a χdistribution with the degrees of freedom of the measurement vector’s dimension,providing a mechanism to detect the dynamic model uncertainty of a system.Further,since the Mahalanobis distance can be expressed mathematically, it enables the fading factor in the fading filter to be determined without involving artificial empiricism.However,there has been very limited research on drawing the concept of Mahalanobis distance into nonlinear system state estimation using CKF to improve the filter’s adaptability.

This paper presents a novel methodology of fading CKF with augmented mechanism to address the problems involved in tightly-coupled INS/CNS integration for HV navigation.The novelty of this method is: (A) the technique of state augmentation is combined with the conventional CKF to establish an augmented CKF to decrease the negative effect of nonadditive noise in inertial measurements; and(B)using the theory of Mahalanobis distance, a technique for detection of dynamic model uncertainty is developed and a fading factor is rigorously derived without artificial empiricism to improve the augmented CKF to handle dynamic model uncertainty.Simulations and comparison analysis have been conducted to comprehensively evaluate the performance of the proposed methodology for HV navigation with tightly-coupled INS/CNS integration.

2. Hypersonic vehicle autonomous navigation with tightlycoupled INS/CNS integration

As shown in Fig. 1, the tightly-coupled mode of INS/CNS integration directly uses the observation information (elevation angle) of the target navigation stars as the system measurement to correct the position error of INS, thus effectively avoiding computational errors from CNS in the traditional loosely-coupled mode of INS/CNS integration.

2.1. Dynamic modelling

Denote the geocentric inertial frame by i-frame, the body frame by b-frame, and the Earth frame by e-frame. The navigation frame(n-frame) is chosen as the local geography frame(g-frame),whose origin is at the location of the navigation system,z axis points upward at the local Earth surface referenced position location, x axis points to East and y axis to North.Due to the effect of various error sources,there are some angular rotation errors between the real (n-frame) and computed navigation frame (n-frame). The dynamic model consists of attitude, velocity, position and IMU errors.

2.1.1. Attitude error equation

Fig. 1 Implementation of the tightly-coupled INS/CNS integration.

Remark 1. It can be seen from Eq. (13) that the nonlinear transformation involves non-additive noise, making the estimated state also involve nonlinear noise terms. However, the conventional CKF is originally derived under the assumption of additive noise, which does not hold for tightly-coupled INS/CNS integration, thus degrading the CKF filtering accuracy.

2.2. Measurement modelling

The basic principle of CNS for vehicle positioning is to observe the navigation star’s elevation angle and azimuth angle relative to the n-frame. According to the spherical triangle cosine theorem,the following relationship can be achieved

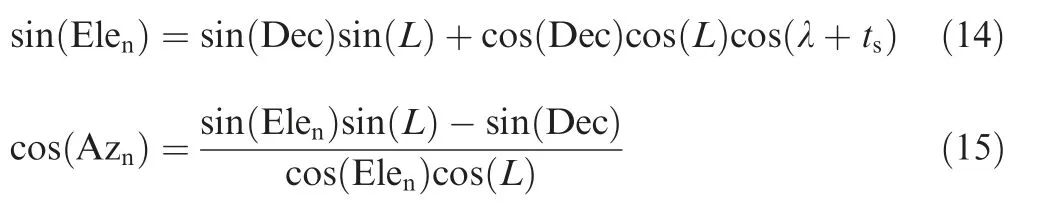
where Eleand Azare the navigation star’s elevation angle and azimuth angle relative to the n-frame;L and λ are the vehicle’s latitude and longitude; Dec is the declination of the navigation star; tis the Greenwich hour angle of the navigation star, which can be obtained from the astronomical almanac given specific time.

We can see that if elevation angle information from two or more different navigation stars is used at each moment, Eq.(14)is sufficient to estimate the vehicle’s position.The navigation star’s elevation angle relative to the b-frame,namely Ele,can be directly measured by star image processing, star center extraction and navigation star identification in CNS. A transformation between Eleand Eleis described as

3. Mahalanobis distance-based fading cubature Kalman filter with augmented mechanism

This section presents a methodology of fading cubature Kalman filter with augmented mechanism for tightly-coupled INS/CNS integration. It develops an augmented CKF to handle the non-additive noise involved in tightly-coupled INS/CNS integration. In addition, it derives a new fading factor based on Mahalanobis distance and further embeds this fading factor into the augmented CKF to hinder dynamic model uncertainty for improving the filter’s adaptability for tightlycoupled INS/CNS integration.

3.1. Augmented cubature Kalman filter

Consider the following nonlinear system described as Eq.(13)and Eq.(20)

where E［·］ represents the expectation of a variable, Qis usually a non-negative definite matrix, Ris generally a positive definite matrix, and δstands for the Kronecker-δ function.

The conventional CKF is derived under the assumption of additive noise,which suffers from accuracy degradation in the presence of non-additive noise. This paper adopts the technique of state augmentation to address this problem, leading to an augmented CKF for tightly-coupled INS/CNS integration. The computational process of augmented CKF can be described as:

Step 1. Initialization. Augment the dynamic noise into the system state to extend the state dimension

Since wis a Gaussian noise sequence and independent of Z, the state estimation and its error covariance in the previous time step k-1 can be written as

The associated auto-covariance and cross-covariance are formulated as

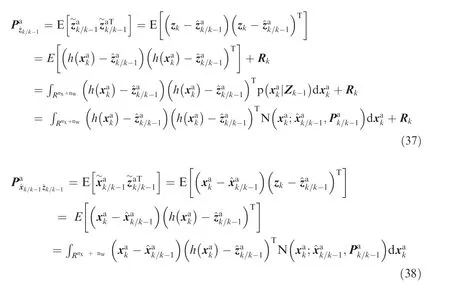
Using the cubature rule, the measurement prediction, its auto-covariance and cross-covariance matrices are calculated as

3.2. Mahalanobis distance-based fading cubature Kalman filter with augmented mechanism

Assumption 1.The accuracy of the system measurement model can be guaranteed using highly accurate CNS measurement devices or a large amount of redundant observation data by multiple navigation stars for tightly-coupled INS/CNS integration.In contrast, since the dynamic model used is only a theoretical approximation to the real-world system, it inevitably involves error, which is usually difficult to tackle. Due to this reason,this paper assumes that the accuracy of the system measurement model is guaranteed for tightly-coupled INS/CNS integration, i.e., only the dynamic model uncertainty is considered in this paper.

Based on the above assumption, this section develops a novel method of Mahalanobis distance for detection of dynamic model uncertainty involved in the tightly-coupled INS/CNS integration. It also derives a new fading factor and further embeds this factor into the augmented CKF, resulting in an augmented fading CKF to improve the filter’s adaptability to hinder dynamic model uncertainty in tightly-coupled INS/CNS integration.

Remark 3.From the hypothesis testing in Eq.(54),it can be seen that when α is chosen as a very small value,if the judging index γis larger than the quantile χ, the null hypothesis in Eq. (54) will be violated, denoting that there is a very high probability （1-α） that dynamic model uncertainty is present in the nonlinear system Eq.(22).In this case,a new fading factor based on Mahalanobis distance will be derived and embedded into the augmented CKF to improve the filter’s adaptability to hinder the influence of dynamic model uncertainty in tightly-coupled INS/CNS integration.

Remark 4.It should be noted that the selection of the quantile χis highly correlated with the significance level α,which implies a probability for incorrectly rejecting the null hypothesis.Thus,the larger the α value is,the smaller the quantile χis,and the higher the target probability Eq.(53)is.However,if the α is chosen too large, it will lead to the false detection for the case of without dynamic model uncertainty. In practice, α is generally chosen as 0.05 to balance the accuracy and robustness,since if the target probability Eq.(53)is less than or equal to 0.05, the alternative hypothesis will be a rare probability event.

3.2.2. Determination of fading factor

After the dynamic model uncertainty is detected by the hypothesis testing described in Section 3.2.1, a simple method will be established by introducing a time variant fading factor λinto the predicted state covariance matrix to inflate the predicted state covariance to weaken the influence of dynamic model uncertainty.

Modify the predicted state covariance as

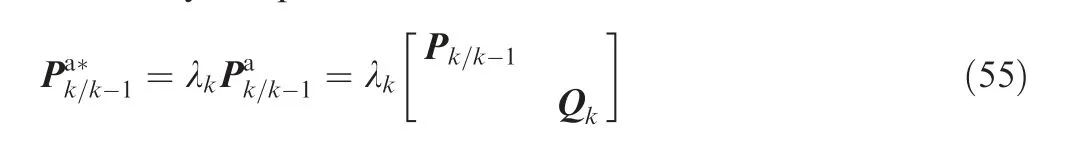
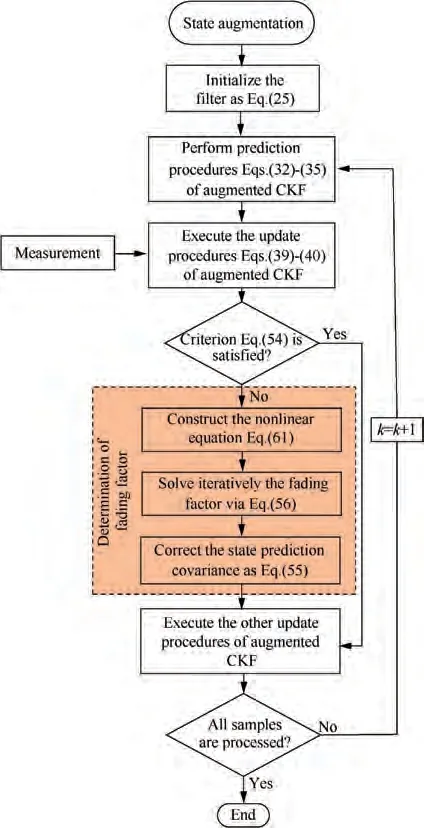
Fig. 2 Procedure of the proposed AFCKF.

(2) Else,

• Substitute the fading factor λinto Eq. (33) and construct the nonlinear Eq. (61).

• Solve iteratively the fading factor λvia Eq. (56) using the chord secant theory.

• Correct the state prediction covariance by Eq. (55).

• Execute the update procedure of the augmented CKF to calculate system state estimation ^xand its associated error covariance Pvia Eqs. (39)-(46).

Step 4.Get back to Step 2 for the next time step to process all the samples.

4. Simulation validation and performance evaluation

Simulation validation has been conducted to comprehensively evaluate the performance of the proposed AFCKF for HV navigation with tightly-coupled INS/CNS integration in the presence of non-additive noise and dynamic model uncertainty. The results in the simulation also effectively reflect the efficacy of the proposed method in the real-world environment since the authenticity of the simulation parameters are consistent with real-world such as flight trajectory, sensors accuracy and so on. Comparison analysis of the proposed AFCKF with the conventional EKF and conventional UKF(written in short as EKF and UKF in the following)as well as the conventional CKF, augmented CKF and iterative CKFis also discussed in this section.

As depicted in Fig. 3, a hypersonic vehicle flight trajectory is designed according to an actual flight process, which includes typical maneuver conditions such as taking off,climbing, turning, accelerating and pitching. The cruise altitude is about 35000-45000 m, the maximum speed is 10 Mach, and the flight simulation time is 1200 s. The initial attitude of HV is 0◦, 0◦and 0◦in pitch, row and yaw, the initial velocity is 0 m/s,1700 m/s and 0 m/s in East,North and Up,and the initial position is 107.997◦, 32.046◦and 35000 m in longitude, latitude and altitude.To simulate the dynamic maneuvering of the HV, small attitude changes with unequal cycle and amplitude are added in the hypersonic cruise stage.

The parameters for the inertial sensors and CNS star observation used in the tightly-coupled INS/CNS integration are shown in Table 1.The altitude of the HV is aided by an altimeter with the noise of 25 m.The initial parameters for the filters are given in Table 2. There are two navigation stars observed simultaneously in the simulation case. Thus, χin the proposed AFCKF is set as 5.991 from the χdistribution table with the reliability of 95% (α = 0.05) and under 2 degrees of freedom. Moreover, the commonly used least-square estimate technology was also adopted for time synchronization to process the asynchronous data of INS and CNS.

Four typical dynamic model uncertainties, i.e., state saltation,inaccurate dynamic model,incorrect initial state and perturbed non-Gaussian dynamic noise, are considered in the simulation case to evaluate the performance of the proposed AFCKF in comparison with EKF and UKF as well as the conventional CKF,augmented CKF and iterative CKF.The Root Mean Square Error(RMSE)with 20 Monte-Carlo runs is used to quantify the performances of all the filters,which is defined as where Adenotes the error vector of the position parameters at the ith Monte-Carlo run.

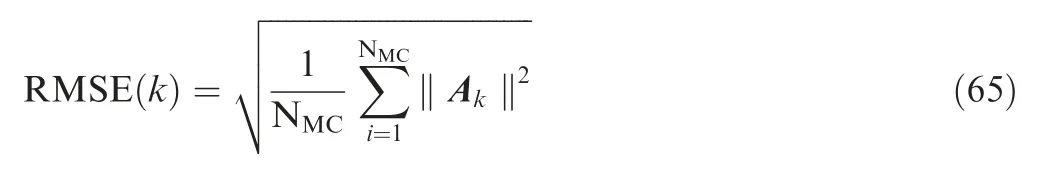
Fig. 3 HV flight trajectory.

Table 1 Sensors parameters.

Table 2 Initial parameters.

4.1. Dynamic model uncertainty

Case 1. State saltation Suppose that the initial state is selected as Tables 1 and 2.To evaluate the performance of the proposed AFCKF in terms of state saltation, a small state saltation is introduced into the time step k=400, i.e.,

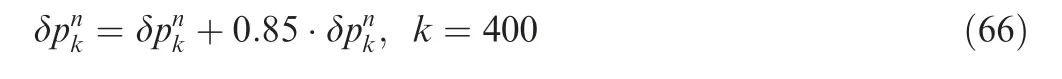
Fig. 4 Judging index γk for the filtering process in the case of state saltation.

Fig. 4 shows the judging index γgiven by Eq. (51) for the proposed AFCKF in this case. It can be seen that when the state saltation appears at time step k=400,the judging index γsignificantly increases and exceeds the threshold, verifying that the proposed AFCKF can effectively detect the dynamic model uncertainty(state saltation)using the concept of Mahalanobis distance.

The RMSEs of HV position by each filter are depicted in Fig. 5. Before the state saltation occurs, the position error of EKF is largest among all the filters due to the involved linearization error of system model.UKF improves the EKF performance by using the unscented transformation to approximate the posteriori distribution of system state, and its position error is much smaller than that of EKF.However,since UKF is unstable for high-dimensional nonlinear integrated systems, the improvement of UKF is still limited compared to the conventional CKF.Further,the position error of the conventional CKF is significantly larger than that of the augmented CKF.This is because the conventional CKF treats the non-additive noise as additive noise for the dynamic model,decreasing the navigation accuracy. The iterative CKF improves the conventional CKF through the dynamic noise estimation, leading to a similar filtering performance as the augmented CKF. Moreover, using the detection of dynamic model uncertainty, the proposed AFCKF can also obtain a similar level of estimation accuracy as the augmented CKF.

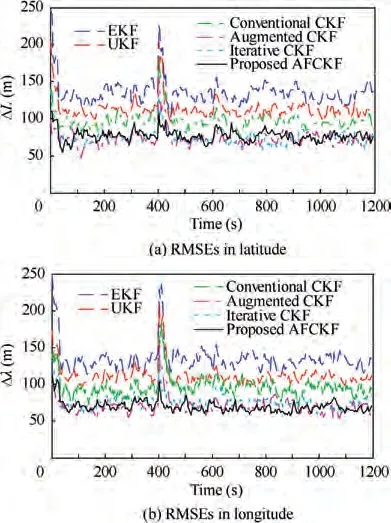
Fig. 5 Position RMSEs of HV for the case of state saltation.

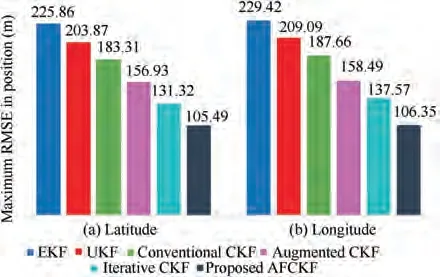
Fig. 6 Position RMSEs at time k=400 for the HV.

When the abrupt change occurs at k=400, the RMSE curves of each filter exhibit large jumps, which can be explained as the mismatch between the dynamic model and the real dynamic system.The RMSEs of HV position for each filter at k=400 are intuitively compared in Fig. 6. It can be seen that similar as the time periods without state saltation,the position RMSEs of EKF and UKF are much larger (at least 22.25%and 11.22%larger)than that of the conventional CKF,while the position RMSE by the augmented CKF is significantly smaller (at least 14.39% smaller) than that of the conventional CKF. The iterative CKF hinders the influence of state saltation on the navigation solution through the noise statistics estimation,leading to a smaller estimation error than the conventional and augmented CKFs. However, since this method treats the state saltation as dynamic noise uncertainty and determines the forgetting factors by empiricism,the resultant accuracy improvement is limited. By contrast, the proposed AFCKF results in the smallest position RMSE due to the advantage of the augmented filtering form and the involvement of fading factor without empiricism.Its position RMSEs are 19.67% and 22.69% smaller than those of the iterative CKF in latitude and longitude.Moreover,after the state saltation disappears, the proposed AFCKF also has a faster convergence speed than the other five filters to revert to the normal error interval.

Case 2. Inaccurate dynamic model

Suppose that there is small inaccuracy involved in the dynamic model as follow

The other conditions remain the same as in Tables 1 and 2,and the RMSEs in position by each filter are shown in Fig. 7.

It can be seen from Fig. 7 that since the dynamic model becomes inaccurate, EKF and UKF as well as the conventional CKF and augmented CKF lose the capability to track the inaccurate model. Thus, their position RMSEs are significantly larger than the iterative CKF and proposed AFCKF.On the contrary, by introducing the fading factor, AFCKF can adjust the gain matrix in real time according to the change of innovation information when the dynamic model is inaccurate, leading to improved estimation accuracy. Its position RMSE is also smaller than that of the iterative CKF.

To further evaluate the performance of the proposed AFCKF,the accumulative RMSEs of each filter are also computed and presented in Fig. 8 for intuitive comparison. The Accumulative RMSE (ARMSE) is defined as

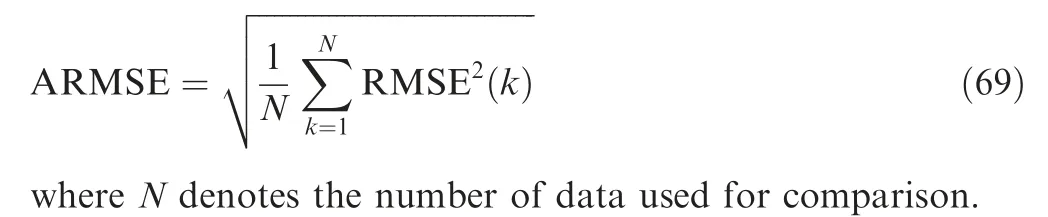
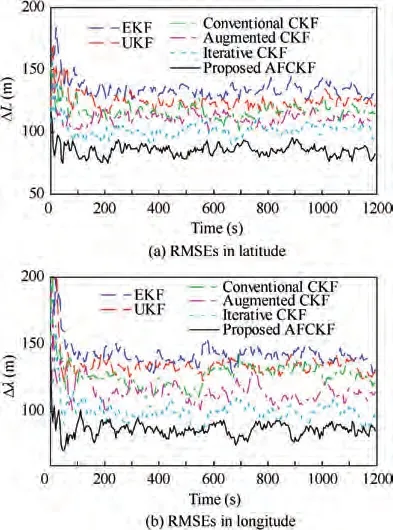
Fig. 7 Position RMSEs of HV for the case of inaccurate dynamic model.

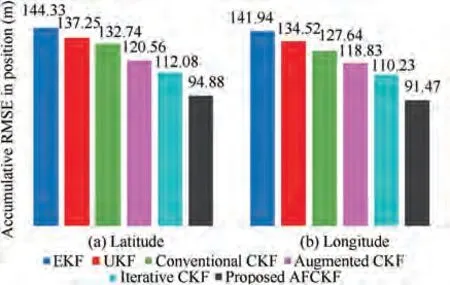
Fig. 8 Accumulative position RMSEs for the HV.

Fig. 8 shows that the position ARMSEs of AFCKF in latitude and longitude are 34.26%and 35.56%smaller than those of EKF,30.87%and 32%smaller than those of UKF,28.52%and 28.34% smaller than those of the conventional CKF,21.3% and 23.02% smaller than those of the augmented CKF, and 15.35% and 17.02% smaller than those of the iterative CKF. This denotes that AFCKF has a stronger adaptability to track the inaccurate dynamic model, resulting in higher navigation accuracy.

Case 3. Incorrect initial state

For the case that the dynamic model involves incorrect initial state,the initial state of the position error for all the filters is set to an obvious deviation of 10 times larger than its real initial state. The other simulation parameters are given in Tables 1 and 2.

The RMSEs in latitude and longitude of each filter are illustrated in Fig. 9. It can be seen that the results for the case of incorrect initial state have a similar phenomenon as in the case of state saltation. The convergence speed of the proposed AFCKF is much higher than those of EKF and UKF as well as the conventional CKF,augmented CKF and iterative CKF,indicating the strong ability of the designed fading factor to quickly track the abnormal state. Fig. 10 presents the RMSE ratios in latitude and longitude by the above six filters during the time interval(1 s,60 s),where the results of EKF are taken as the relative benchmark. It also validates that the proposed AFCKF has a much smaller position error than those of the other five methods at the beginning of filtering stage, leading to improved convergence in this case.

Case 4. Perturbed non-Gaussian dynamic noise

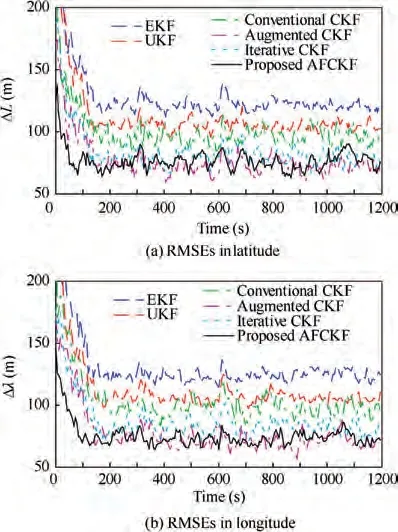
Fig. 9 Position RMSEs of HV for the case of incorrect initial state.

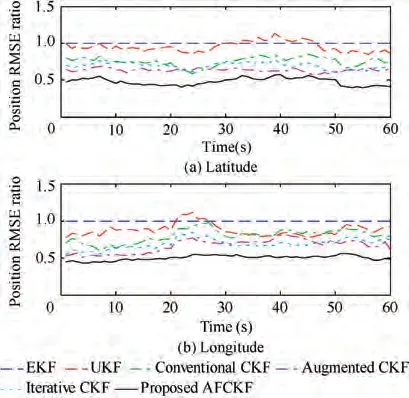
Fig. 10 Position RMSE ratios of HV during the time interval from 1 s to 60 s for the case of incorrect initial state.

Due to the highly dynamic flight and complex flight environment, the actual noise of HV navigation is always non-Gaussian. Since the non-Gaussian noise can be described by a Gaussian mixture distribution,the nominal Gaussian distribution of the dynamic noise is assumed to be perturbed by another Gaussian distribution, leading to a perturbed non-Gaussian noise in this case to evaluate the capability of the proposed AFCKF in handling dynamic noise uncertainty

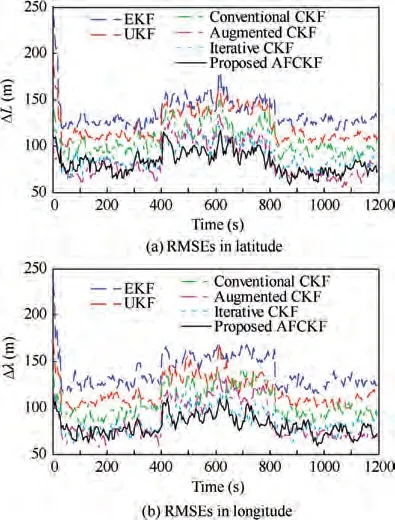
Fig. 11 Position RMSEs of HV for the case of perturbed non-Gaussian dynamic noise.

Fig. 12 Position MSEs of HV during the time interval (400 s,800 s) for the case of perturbed non-Gaussian dynamic noise.

The position RMSEs of each filter are depicted in Fig. 11.During the time interval (400 s, 800 s), EKF and UKF as well as the conventional CKF,augmented CKF and iterative CKF have a serious jump from the normal error interval due to the influence of the perturbed non-Gaussian dynamic noise.This is because they have a poor ability to inhibit the disturbance of non-Gaussian noise,leading to a larger navigation error.However, the proposed AFCKF can detect and compensate the dynamic model uncertainty through the concept of Mahalanobis distance, leading to improved estimation accuracy.

To further evaluate the performance of the proposed AFCKF, the Mean Square Errors (MSEs) of each filter in terms of Monte Carlo runs during the time interval (400 s,800 s) are also illustrated in Fig. 12. The MSE in terms of Monte Carlo runs is defined as

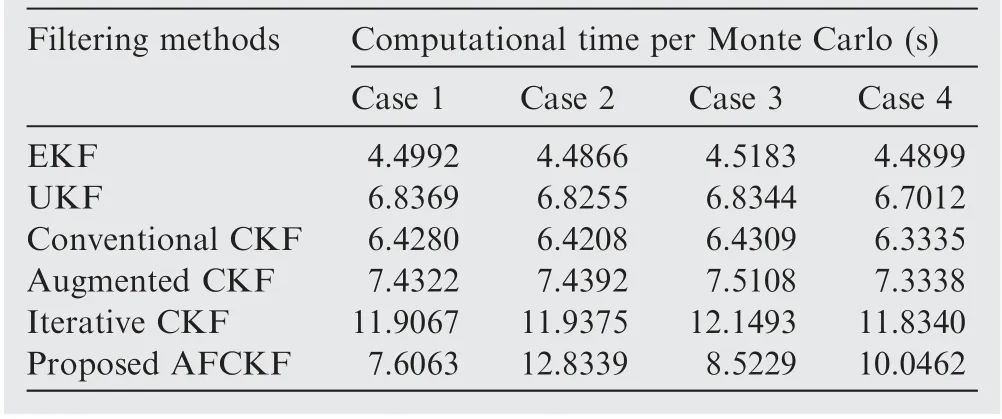
Table 3 Computational time per Monte Carlo run of EKF,UKF as well as conventional CKF, augmented CKF, iterative CKF and proposed AFCKF.

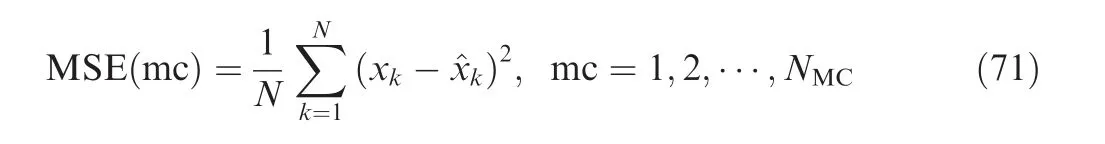
Fig. 12 shows the MSEs of HV position by each filter. It is also evident that the proposed AFCKF outperforms the other five filters for the case of perturbed non-Gaussian dynamic noise.

4.2. Computational performance

Monte Carlo simulations were also carried out on an Intel(R)Core(TM)i5-9400F 2.9G Hz PC with 16 GB memory to study the computational performance of the proposed AFCKF for the above four types of dynamic model uncertainty. Table 3 gives the computational times, i.e., the filtering times per Monte Carlo run, for EKF and UKF as well as the conventional CKF, augmented CKF, iterative CKF and proposed AFCKF. Further, the computational efficiencies of UKF as well as the conventional CKF, augmented CKF, iterative CKF and proposed AFCKF relative to that of EKF are calculated and intuitively compared in Fig.13 to eliminate the effect from the differences in terms of computer and processor.

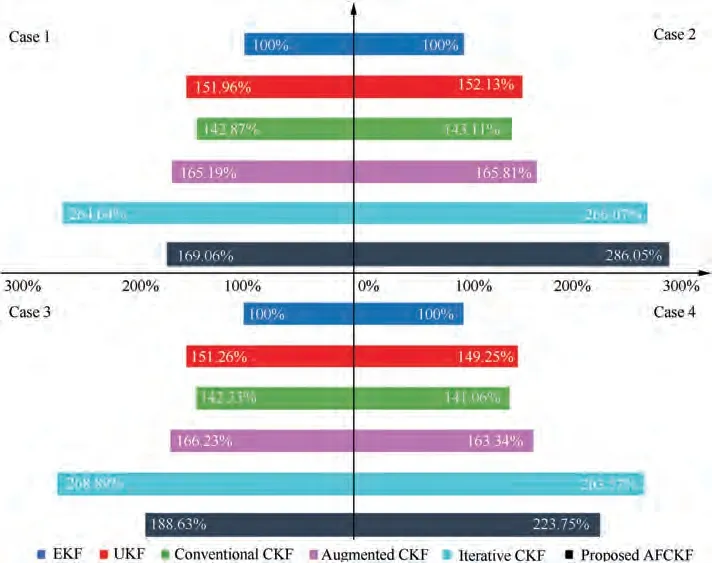
Fig. 13 Relative computational efficiencies of EKF, UKF as well as the conventional CKF, augmented CKF, iterative CKF and proposed AFCKF.

Table 3 and Fig. 13 show that EKF has the shortest computational time among all the filters for the above four types of dynamic model uncertainty.Since a vast number of calculations are involved in the unscented transformation,the computational time of UKF is at least 49.25% larger than that of EKF. By contrast, because of the advantage of cubature rule in the number of cubature points, the conventional CKF’s computational time is shorter than that of UKF at least 5.49%, while the computational time of the augmented CKF is at least 15.62% larger than that of the conventional CKF due to the augmented system state. Further, the iterative CKF’s computational time is significantly larger than that of the augmented CKF,leading to at least 60.2%time consumption compared to the augmented CKF.This is because the iterative CKF involves a complex computational process for the dynamic noise statistics estimation at all time steps. In Case 2, due to the computation of the fading factor for all time steps, the computational time of the proposed AFCKF is slightly larger than that of the iterative CKF. However, in the other cases, the proposed AFCKF avoids the redundant computation of the fading factor at the time steps without dynamic model uncertainty through its detection process,leading to higher computational efficiency than the iterative CKF.The above results demonstrate that the proposed AFCKF can obtain a faster computing speed than the iterative CKF through the detection of dynamic model uncertainty, and it is not difficult for today’s computation power to be able to afford these increased computational efforts for the proposed AFCKF compared to the EKF, UKF, conventional CKF and augmented CKF, which is sufficient to achieve the realtime performance for HV navigation with tightly-coupled INS/CNS integration.

The above simulation results and comparison analysis indicate that the proposed AFCKF can effectively detect dynamic model uncertainty and suppress its influence on filtering estimation,leading to higher navigation accuracy than EKF and UKF as well as the conventional CKF,augmented CKF and iterative CKF.Moreover,AFCKF can also achieve the real-time performance for HV navigation with tightly-coupled INS/CNS integration.

5. Conclusions

The contributions of this paper are

(1) An augmented CKF is developed by combining the technique of state augmentation into the conventional CKF to decrease the negative effect of non-additive noise involved in the dynamic model.

(2) It establishes a technique for detection of dynamic model uncertainty and rigorously derives a fading factor based on the theory of Mahalanobis distance without artificial empiricism to improve the augmented CKF to tackle the dynamic model uncertainty.

(3) Simulation results and comparison analysis validate that the proposed methodology can effectively curb the adverse impacts of non-additive noise and dynamic model uncertainty for inertial measurements, leading to higher navigation accuracy than EKF and UKF as well as the conventional CKF, augmented CKF and iterative CKF for HV navigation with tightly-coupled INS/CNS integration.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

This study was co-supported by the National Natural Science Foundation of China (Nos. 41904028, 42004021), the Natural Science Basic Research Plan in Shaanxi Province of China(Nos. 2020JQ-150, 2020JQ-234) and the Soft Science Project of Xi’an Science and Technology Plan (No. XA2020-RKXYJ-0150).