A multi-frame track-before-detect algorithm based on root label clustering for multiple targets

Jiqi ZHANG, Hihong TAO, Xiushe ZHANG, Chunlei HAN

a State Key laboratory of Radar Signal Processing, Xidian University, Xi’an 710068, China

b Xi’an Research Institute of Navigation Technology, Xi’an 710071, China

KEYWORDS Multi-frame track-beforedetect;Multiple targets detection;Root label clustering;State transition set;Track extrapolation

Abstract In this paper, a novel multi-frame track-before-detect algorithm is proposed, which is based on root label clustering to reduce the high computational complexity arising by observation area expansion and clutter/noise density increase.A criterion of track extrapolation is used to construct state transition set,root label is marked by state transition set to obtain the distribution information of multiple targets in measurement space, then measurement plots of multi-frame are divided into several clusters, and finally multi-frame track-before-detect algorithm is implemented in each cluster. The computational complexity can be reduced by employing the proposed algorithm. Simulation results show that the proposed algorithm can accurately detect multiple targets in close proximity and reduce the number of false tracks.

1. Introduction

Multiple targets tracking plays a significant role in air defense area in recent years.It has gained many research achievements.Conventional multiple targets tracking algorithmsuse detection threshold, from which the significant measurement plots with sufficient strength are retained and the weak measurement plots are discarded, so as to achieve the target trajectory estimation. However, these algorithms show great limitations when the target Signal-to-Noise Ratio (SNR) is low. Because the information is irreversibly lost after detection threshold or lowering detection threshold results in too many false tracks, Track-Before-Detect (TBD) algorithmsdirectly process the raw measurement plots or low threshold measurement plots. These algorithms achieve superior performance for tracking low SNR targets by accumulating the power of several consecutive frames of measurement plots.TBD algorithms can be classified into two classical categories: Single Frame Recursive TBD (SFR-TBD)and Multi-Frame TBD (MFTBD).MF-TBD has simple structure and is easy to implement. Various aspects of MF-TBD have been studied, such as maneuvering target tracking,multiple targets trackingand multiple sensors fusion.Consequentially,clutter distributionand the target fluctuating characteristicsalso have been extended to MF-TBD.

A major drawback of MF-TBD is its potentially high computational complexity in multiple targets tracking application.Many algorithms have been proposed to reduce the high computational complexity of MF-TBD.It may be divided into two categories. The first category focuses on improving implementation efficiency of a single batch,which adds a preprocessing step to reduce the amount of measurement plot.The second category takes into account the repetitive calculation caused by sliding window processing,which is essential for tracking continuous target trajectories over a long time period. However, with the enlarging of observation area and the increase of clutter/noise density, all the above algorithms are hardly to face the predominant challenge that the correlative computation of measurement plots is significantly increased. In this paper, a novel MF-TBD based on Root Label Clustering (RLC-MF-TBD) is proposed to detect air weak targets, which can divide the multi-frame measurement plots into several clusters. MF-TBD is independently implemented in each cluster. Performance analysis and simulation results show that RLC-MF-TBD can accurately detect multiple targets in close proximity, and reduce the computational complexity.

The rest of this paper is organized as follows. Models and notations are presented in Section 2. In Section 3, MF-TBD is proposed and analyzed. Section 4 shows the general framework of the measurement space clustering and a detailed implementation procedure.The analysis of the algorithm computational complexity is summarized. In Section 5, simulation results, demonstrating the efficiency of the proposed algorithm, are presented. In Section 6, conclusion is drawn.

2. Models and notations

2.1. Dynamic model

2.2. Measurement model

The two-stage detection architecture is proposed in Refs.,which does not need a discretization of the measurement space and directly operates on the measurement plots list. At the lth frame, a list of measurement plots can be expressed as

where Hand Hdenote the hypothesis that no target is present in the coverage area and its alternative that a single target is present respectively.In addition,arepresents the target signal amplitude. nand ndenote samples of an independent and identically distributed zero mean Gaussian noise process with variances σand σrespectively.

3. Problem statement

In order to estimate the states of multiple targets,from a Bayesian perspective,the estimated multiple targets states sequence can be found from the posterior density function p(X|Z),which gives a certain estimation criterion. However, the analytic solution for calculation is usually intractable. MF-TBD implements Bayesian filtering in discretized state space R⊂Rand approximates the posterior density.

3.1. Single target MF-TBD

Assume that there is single target,and its state sequence can be found by single target MF-TBD as

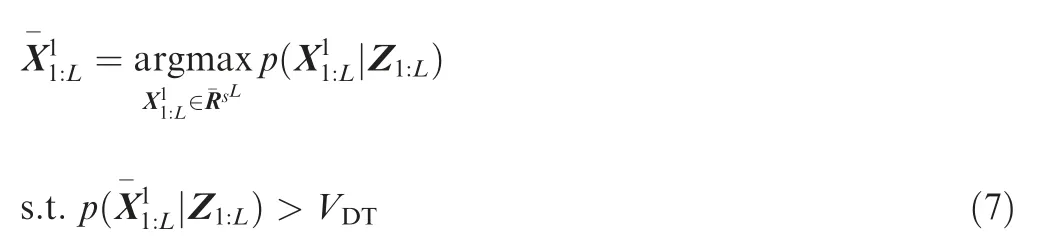
where Vdenotes a detection threshold selected by Monte Carlo experiments under certain false track probability, and L is the number of consecutive frames processed in a multi-

3.2. Multiple targets MF-TBD

By extending the single target MF-TBD to multiple targets scenarios,the states of multiple targets can be estimated.In a scenario with M targets (M > 1), the states estimate of multiple targets based on MF-TBD can be derived as

where I(x|Z) is the merit function of state x, and L(z|x)represents the contribution of measurement plot associated with the state x. The maximization is performed over τ(x)which is a collection of discrete target states at the l-1th frame from which a transition to xis possible.After DP integration,detection is made by testing the global maximum merit with V. However, a predominant limitation for multiple targets MF-TBD is to find a computationally efficient solution, or a rather approximate solution. To reduce the computational complexity, a Two-Stage detection architecture MF-TBD(TS-MF-TBD) was employed to approximately implement the optimal multi-path search by discarding a set of weak measurement plots in Ref., and the process of the two-stage detection architecture is shown in Fig. 1, where the detecting performance of TS-MF-TBD is decreased due to the interference when targets are in close proximity.

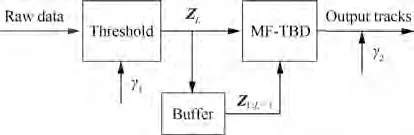
Fig. 1 Process of two-stage detection architecture.

An MF-TBD based on Successive Track Cancellation(STC-MF-TBD) was proposed in Ref.. This algorithm can eliminate the interference measurement plots of targets, which can improve the detecting performance when closely-spaced targets are presented. However, a significant limitation of the STC-MF-TBD is that the global measurement space is searched, because there is no prior information of a motion model that can accurately describe the desirable targets motion. Moreover, the computational complexity is computationally prohibitive with the increasing number of targets and clutter/noise.

For the high computational complexity of the above algorithms,a novel MF-TBD based on measurement space clustering is presented. The measurement space can be divided into several independent measurement sub-spaces by clustering,and then the posterior density satisfies

4. Development of the proposed algorithm

4.1. Framework of measurement space clustering

A multiple targets detection scenario is shown in Fig. 2(a). In such scenario,the correlation of trajectories includes proximity and separation.Relationship between proximity targets can be constructed by sharing measurement plots. The measurement space can be divided into several mutually isolated clusters as shown in Fig.2(b).The algorithmic model and implementation process are presented in the following.

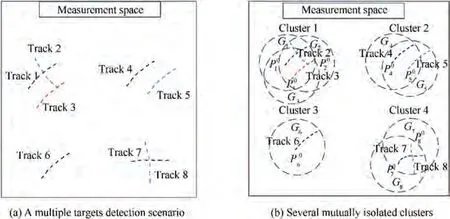
Fig. 2 Multiple targets measurement space.

The clusters Care defined as complete clusters, where‖C‖ is the number of targets in the cluster C.

Although Eq. (8) can be utilized to solve multiple targets detection problem, the computational complexity is prohibitive when observation area is enlarged and clutter/noise density is increased.It is useful to separate measurement plots of multiple targets into complete clusters,which can divide the whole scenario into several local scenarios without correlation.Consequently, these complete clusters are used to split the high-complicated maximization into several low-complicated maximizations. For example, a scenario with M targets can be divided into K (1 ≤K ≤M)complete clusters C.In each sub-cluster C(1 ≤k ≤K),

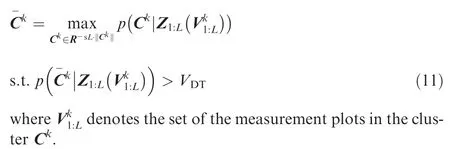
In order to reduce the computational complexity of MFTBD, it is necessary to design an appropriate clustering algorithm which divides measurement plots into several complete clusters. A root label clustering algorithm is presented. The main idea of the proposed algorithm is to obtain the distribution information of multiple targets in the measurement space according to the root label, and then to divide multi-frame measurement plots into several complete clusters.

In order to separate measurement plots, it is necessary to judge the relationship of measurement plots. The maximum velocity constraint algorithm is adopted to judge the relationship between different frame measurement plots, and for any two measurement plots zand zfrom the lth frame and the l + 1th frame, the relationship judgment is given by

For marking measurement plots of measurement space,firstly, measurement plots from the first frame or without previous measurement plots are marked with root label.Secondly,measurement plots from the second frame to the Lth frame are marked successively by state transition set, and the marking process is shown in Fig. 4.

Definition 2. Marking measurement plots of measurement space with root label, for two measurement plots zand zwhich satisfy the relationship judgment with Eq.(12),the root label sets(z)and (z)can be given as

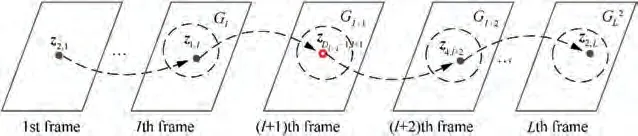
Fig. 3 State transition set construction.

Proposition 1. For a scenario with M targets, if the scenario over L frames can be separated into K(1 ≤K ≤M)clusters Cby root label clustering, the clusters Care complete clusters.

From Eq. (20), it can be found that the intersecting targets Zand Zbelong to the same cluster.For a target Zbelongs to any cluster C,where C∈Cand‖C‖>1,it is assumed that there is no target that intersect with Zin the cluster C,and the cluster Chas only one root label,which conflicts with the supposed condition ‖C‖>1. So the result is that there exists at least one target that intersects with Zin the cluster C. Thus, Proposition 1 is proved.

4.2. Algorithm implementation

In this paper, the RLC-MF-TBD is presented in details as shown in Fig. 5.

4.2.1. Measurement plots clustering

The root label cluster C(k = 1,2,...,K) is used to extract the measurement plots from measurement space Z, and the measurement plots are clustered as where‖C(m,k)‖denotes measurement plots that belong to target m of root label cluster C.

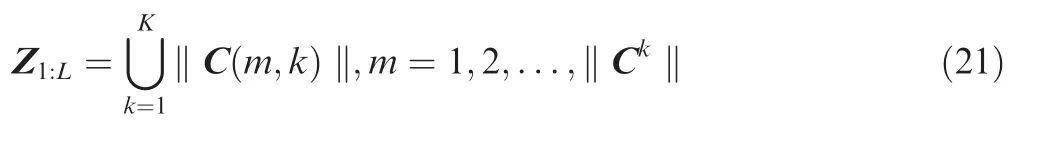
Fig. 4 Process of root label marking.

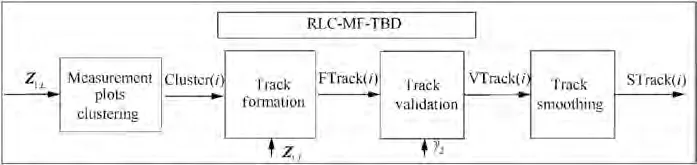
Fig. 5 RLC-MF-TBD architecture.

4.2.2. Track formation

In each sub-cluster, STC-based track formation algorithm is operated by a criterion of track extrapolation, and then the merit function and backtracking state of candidate tracks are computed by accumulating the intensity of the plots from targets

4.2.4. Track smoothing

The validated tracks are smoothed to improve the tracking accuracy.In Ref.34,a joint trajectory smoothing and tracking framework is presented to estimate the target state by continuous function of time. The RLC-MF-TBD pseudo code is shown in Table 1.

4.3. Analysis of computational complexity

The computational complexity of the proposed RLC-MFTBD is determined by the state transition set construction and track formation. Nis the average number of measurement plots in per frame, which can be modeled as the sum of two independent binomial random variables with parameters (NN-N, FAR) and (N, PD). The average computational complexity of RLC-MF-TBD to implement state transition set construction by a criterion of track extrapolation is where Nand Ndenote the number of range and azimuth resolution elements respectively, FAR is the false alarm rate, PD is the probability of detection, and N∈{1,2,..., NN} is the number of targets in this scenario.

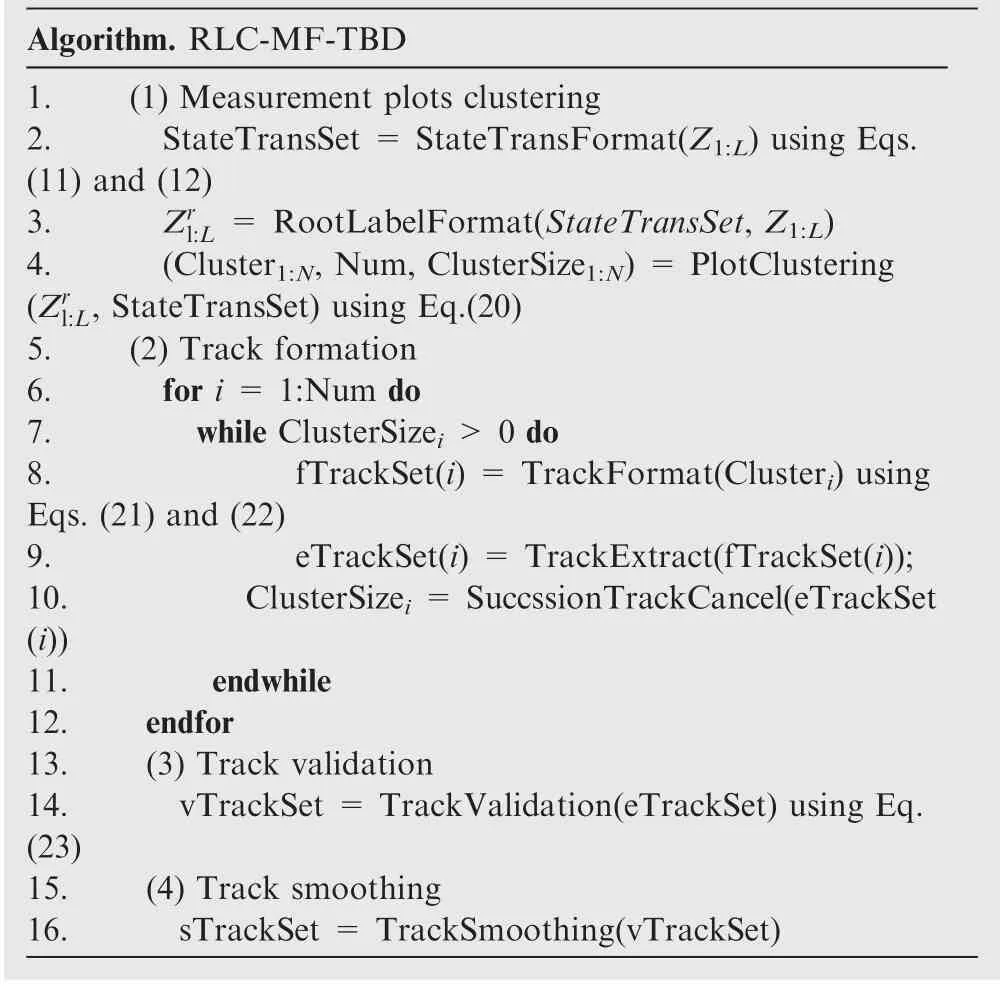
Table 1 RLC-MF-TBD pseudo code.

The relationship of measurement plots from different subclusters is given by

The average computational complexity of STC-MF-TBD to implement track formation is

Table 2 Computational complexity.

5. Simulation example

In order to analyze the detection performance of different algorithms, the assessment measurements include

(1)the number of valid detection(N):the number of true targets that are detected.

(2) the number of lost detection (N): the number of true targets that are not detected.

(3) the number of false detection (N): the number of false targets that are detected as true targets.

The detection performances of TS-MF-TBD, STC-MFTBD and the proposed RLC-MF-TBD are analyzed by the above assessment measurements in a scenario with 12 targets,as shown in Fig. 6. In this scenario, targets move in a 14 km × 14 km observation area. Target1 and Target2, Target7 and Target8 are two groups of parallel motion; Target3 and Target4, Target5 and Target 6 are two groups of crossing motion. All other four targets are a group of approaching motion. The target motions are indicated by the arrows. The number of integrated frames is L=10,the maximum velocity is V= 600 m/s, the maximum number of allowed consecutive missed plots is P=3,the step of the track extrapolation is R = 3, and the time interval is T = 1 s. The first detection threshold Vis chosen to achieve a certain false alarm probability. The secondary detection threshold Vis chosen by 10Monte Carlo experiments.

In Fig. 7, N, Nand Nare plotted versus SNR for P= 10. In Figs. 7 (a) and (b), it can be seen that STCMF-TBD and RLC-MF-TBD perform well. Both the algorithms can correctly detect all targets at high SNRs. Noticeably, the detection performance of TS-MF-TBD is worse than the above two algorithms, because a criterion of track pruning is used in TS-MF-TBD. It cannot correctly detect when targets are in proximity. The number Nof TS-MFTBD and STC-MF-TBD are greater than that of RLC-MFTBD when SNR is lower than 7 dB, which can be seen in Fig. 7(c). The reason is that a criterion of track extrapolation is adopted by RLC-MF-TBD for constructing state transition set using a predefined associated gate, which can govern the constitution of the state transition set to reduce false tracks.A criterion of jumping multi-frame is used by TS-MF-TBD and STC-MF-TBD to construct state transition set with a gradually expanding associated gate which can generate many false tracks.There are few false tracks for all of the three algorithms when SNR is higher than 7 dB,because true targets and false targets can be clearly distinguished by merit function when SNR is higher.

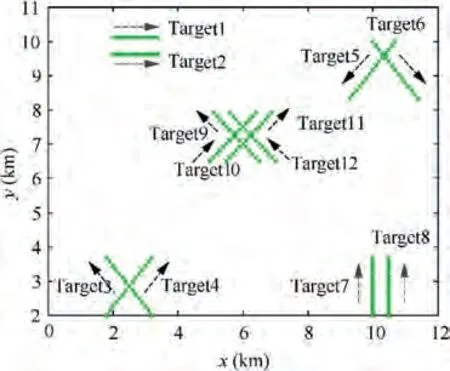
Fig. 6 Simulation scenario.

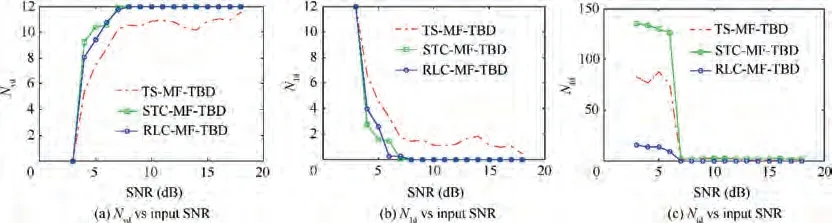
Fig. 7 Comparison of detection performance for Pfa = 10-1.

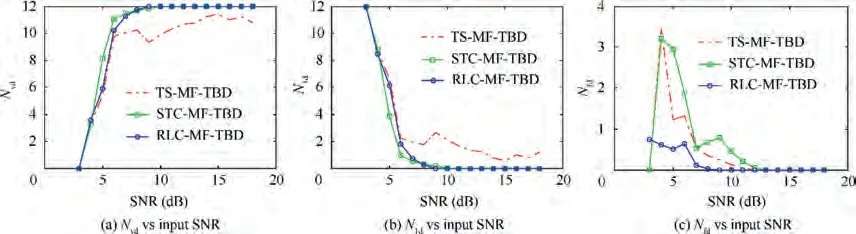
Fig. 8 Comparison of detection performance for Pfa = 10-2.

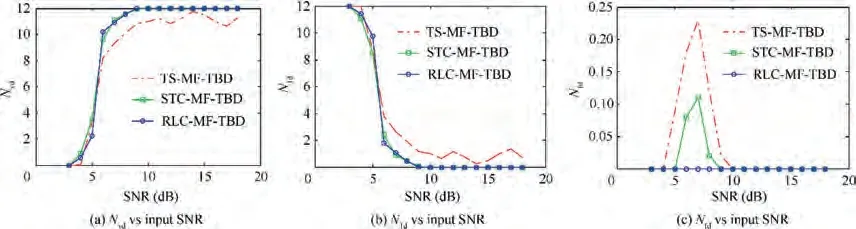
Fig. 9 Comparison of detection performance for Pfa = 10-3.

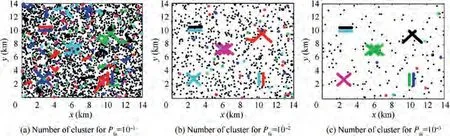
Fig. 10 Comparison of clustering result of RLC-MF-TBD for different input Pfa.

In Figs. 8 and 9, the detection performance of all the three algorithms are plotted versus SNR for P= 10and P= 10. It can be seen that there are a few missed targets for all algorithms due to the higher first detection threshold,when SNR is lower than 7 dB in Figs. 8 (a), (b) and Figs. 9(a), (b). It is indicated that STC-MF-TBD and RLC-MFTBD perform equally well and are better than TS-MF-TBD,when SNR is higher than 7 dB. There are few false tracks for all the three algorithms with low P, which can be seen in Fig. 8(c) and Fig. 9(c), because a large number of false measurement plots are eliminated by a higher first detection threshold.

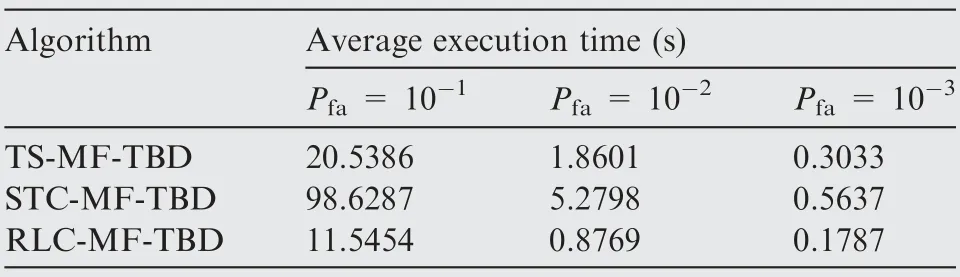
Table 3 Execution time of three algorithms.

In Fig.10,the clustering results of RLC-MF-TBD are plotted for P=10,P=10and P=10,and the number of clusters is 200, 48 and 17 respectively. The cluster is represented by the near measurement plots with the same color,and the measurement plots in different clusters have different colors.It can be seen that with the increase of measurement plots, the number of clustering grows rapidly. The measurement plots of intersecting targets are divided into the same cluster.It is indicated that the RLC-MF-TBD can divide the measurement space effectively.

In Table 3, the average execution time of the MATLAB implementation of the three algorithms are shown for P=10,P=10and P=10.Note that the computational complexity of RLC-MF-TBD is lower than that of TS-MF-TBD and STC-MF-TBD for all P.

6. Conclusions

In this paper, multiple targets detection problem is considered with observation area expansion and clutter density increase for the MF-TBD. Analysis results indicate that the STC-MFTBD suffers from high computational complexity.To overcome this limitation, the RLC-MF-TBD is proposed by dividing multi-frame measurement plots into several clusters, which is capable of achieving low computational complexity.Its implementation was derived in detail and a step-by-step algorithm was presented.Analysis of computational complexity indicates that the proposed algorithm is completely superior to STC-MFTBD. Simulation results and performance analysis show that the proposed algorithm can accurately detect multiple targets in close proximity and reduce the number of false tracks. The computational complexity can be realized in project.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgement

This study was supported by the Innovation Project of Science and Technology Commission of the Central Military Commission, China (No. 19-HXXX-01-ZD-006-XXX-XX).