Efficient adaptive Kriging for system reliability analysis with multiple failure modes under random and interval hybrid uncertainty

Bofan DONG, Zhenzhou LU

School of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China

KEYWORDS Failure probability;Kriging model;Random and interval hybrid uncertainty;System learning function;System reliability

Abstract In the field of the system reliability analysis with multiple failure modes, the advances mainly involve only random uncertainty. The upper bound of the system failure probability with multiple failure modes is usually employed to quantify the safety level under Random and Interval Hybrid Uncertainty (RI-HU). At present, there is a lack of an efficient and accurate method for estimating the upper bound of the system failure probability.This paper proposed an efficient Kriging model based on numerical simulation algorithm to solve the system reliability analysis under RI-HU. This method proposes a system learning function to train the system Kriging models of the system limit state surface. The convergent Kriging models are used to replace the limit state functions of the system multi-mode for identifying the state of the random sample. The proposed system learning function can adaptively select the failure mode contributing most to the system failure probability from the system and update its Kriging model. Thus, the efficiency of the Kriging training process can be improved by avoiding updating the Kriging models contributing less to estimating the system failure probability. The presented examples illustrate the superiority of the proposed method.

1. Introduction

In the field of reliability analysis considering uncertainty,different from single-mode reliability analysis,multi-mode system (can be referred to as system for short) reliability analysis needs to evaluate the safety degree of system on the basis of considering the relationship among multiple failure modes.

At present, most studies on system reliability analysis only consider the random uncertainty,i.e.,the system contains only random variables described by the Probability Density Function (PDF). The reliability analysis methods for the system under the random uncertainty have been well developed, and these methods can be divided into the following three categories,i.e.,the analytical methods,numerical simulation methods and surrogate model methods. The analytical methods include the first-order method of system reliability analysis,the saddlepoint approximation method,and so on. The numerical simulation methods include the Monte Carlo Simulation(MCS),the importance sampling method,and the subset simulation method.Compared with the MCS, the improved numerical simulation such as the importance sampling method and subset simulation method of system reliability analysis greatly reduce the computational effort, but there is still a big gap between the efficiency of the improved numerical simulation and the acceptable range of engineering problems. Recently, the surrogate model methodshave become more and more popular in the field of reliability analysis,and these methods have been applied to system reliability analysis under the random uncertainty.Fauriat and Gaytoncombined adaptive Kriging with MCS to solve the system reliability analysis.Yun et al.proposed an improved U learning function to improve the efficiency of constructing system Kriging models. Recently, Yang et al.used the multimodal adaptive importance sampling and adaptive size of candidate points, and combined these methods with the Kriging models to solve system reliability analysis with small failure probability efficiently.Cheng and Zhaoproposed a chaotic enhanced colliding bodies optimization algorithm for parallel system reliability analysis. Bian et al.used the interdependent competing failure processes to solve the reliability analysis for multi-component systems.

Although it is a popular classical method to consider the random uncertainty in the system reliability analysis,the available information usually cannot give the accurate PDF of all uncertainties that affect the structure reliability, and some of these uncertainties can only be described by the intervals characterized with upper and lower bounds.For general structure,the random and interval inputs coexist widely.Thus, it is necessary to establish the reliability analysis methods under the Random and Interval Hybrid Uncertainty (RI-HU) to evaluate the structure safety. At present, there have been extensive studies on single-mode reliability analysis under RI-HU, such as the double-loop nesting model proposed by Du et al.,and the adaptive Kriging method proposed by Yang et al.

Similar to single-mode reliability analysis, the failure probability of the system is also an interval variable with upper and lower bounds under RI-HU. In practical engineering applications,the upper bound of failure probability is generally more concerned since it’s a conservative evaluation of the safety degree. Thus, this paper only studies the upper bound of the multi-mode system failure probability and regards it as the safety measure index of the multi-mode system under RIHU.At present,the studies on system reliability analysis under RI-HU has not been well solved.Although the numerical simulation methods for system reliability analysis with only random uncertainty can be easily applied to the estimation of the system failure probability under RI-HU, the computational cost of the direct numerical simulation methods is unacceptable to complex engineering problems. Adduri and Penmetsaproposed a function approximation strategy,which reduces the computational cost by constructing an approximate function of the limit state function for each failure mode, but because the contribution of each failure mode to the failure probability of the system under RI-HU is different, indiscriminately constructing the approximate limit state functions of all modes may result unnecessary amount of computational cost.

For the system with random uncertainty, Ref.proposed three different strategies to construct the adaptive Kriging model based MCS to establish the AK-MCSmethod for estimating the system failure probability. The first strategy is to construct and update the Kriging model of each mode indiscriminately, obviously, it’s not the optimal strategy. The second strategy is to transform the limit state functions of the system into an extreme limit state function according to the series and parallel relationship among the modes of the system,on which the AK-MCS method for single-mode reliability analysis is employed to solve the failure probability of the multi-mode system. However, at different realizations of the input variables, the extreme limit state function value may come from different failure modes, which leads to the discontinuity of the extreme limit state function. It’s difficult to construct the discontinuous extreme limit state function accurately. The third strategy is to only update the limit state function of the extreme mode on the basis of the first strategy,which is most efficient of the three strategies.This strategy will be affected by the accuracy of the initial Kriging model of each mode,and the lower accuracy of the initial Kriging model may lead the extreme model to be misjudged converge to the wrong result. Ref.proposed an improved learning function to update the Kriging model of the most easily identified mode of the system,and this learning function can ensure the correct identification of the state of each sample point and avoid the wrong results that may be caused by the third strategy.

Based on the above methods combining the adaptive Kriging model with the numerical simulation for the system reliability analysis under the random uncertainty, this contribution firstly establishes the AK-MCS method for estimating the system failure probability under RI-HU,then a system learning function is proposed to improve the efficiency of training the Kriging models of the system limit state surface and establishes an advanced AK-MCS method (aAK-MCS).By judging the relationship between the state of the system and the state of each mode at the candidate random sample point, the proposed system learning function can adaptively select and update the Kriging model that currently contributes most to estimating the system failure probability. On the premise of correctly identifying the state of each random candidate sample, the proposed aAK-MCS can avoid updating the Kriging models contributing less to estimating the system failure probability. Thus, compared with AK-MCS, the efficiency of estimating the system failure probability under RIHU can be further improved on the basis of ensuring the accuracy.

The main contents of this contribution are organized as follows.Section 2 introduces the system reliability analysis model and the definition of the system failure probability under RIHU. Section 3 introduces the basic idea and implementation steps of the MCS and AK-MCS for estimating the system failure probability under RI-HU. Section 4 proposed the system learning function and the efficient aAK-MCS method. In Section 5, five examples are employed to illustrate the accuracy and efficiency of the proposed methods.Section 6 draws the conclusion.

2. Multi-mode system reliability analysis model under RI-HU

3. MCS and AK-MCS for estimating Pf·series and Pf·parallel

For estimating Pof the series system, the MCS method first needs to generate the random sample pool S=｛x，x，...，x｝ according to f（x） and disperse the discrete interval sample pool S=｛y，y，...，y｝ in ［y，y］.The failure domain indicator function value at the random variable sample point xcan be obtained by Eq. (11).

For the reliability analysis with low system failure probability under RI-HU,the MCS method requires a large sample size Nand N, so it’s not suitable to apply the MCS method to complex engineering problems. In this section, the AK-MCS method for estimating system failure probability under RIHU will be established. The basic ideas are as follows.

Note that the upper bound of failure probability of the kth single mode with g（X，Y） under RI-HU is P, and Pis shown in following Eq. (13).

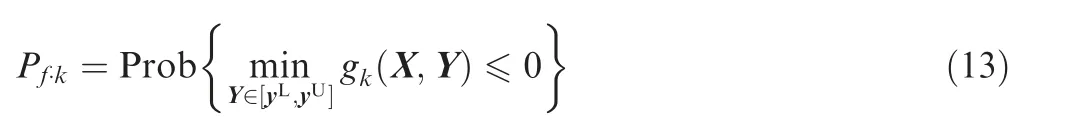
Construct and update each Kriging model g（X，Y） of g（X，Y） until convergence, then g（X，Y） can be accurately used to estimate the failure probability Pof each single mode. Then the system limit state functions ｛g（X，Y），k=1，2，...，m｝ are replaced by the convergent Kriging models｛g（X，Y），k=1，2，...，m｝,and the system failure probability is estimated by the MCS method.

The basic theory about the Kriging model can be seen in Refs.The detailed steps to estimate Pby the AKMCS method under RI-HU are given as follows.

Remark 1. The number of the initial training samples Ndepends on the complexity of the problem. For the complicated problem that the performance functions with multiple random and interval variables are implicit, Nshould be reasonably large to ensure the initial system Kriging models have high surrogating precision. For the problem with simple performance functions and small number of variables, Ncan take a small value.

Similar to the MCS and AK-MCS methods for estimating the series system failure probability under RI-HU, the MCS and AK-MCS methods for estimating the parallel system failure probability Pand the failure probability Pof the system containing an arbitrary relationship can be established on the basis of Eqs. (5)-(10). For the sake of brevity,these steps for estimating Pand Pare omitted.

4. Advanced AK-MCS method for estimating Pf·series and Pf·parallel

The above AK-MCS method to indiscriminately construct and update Kriging models of all modes is not the optimal strategy.Since the effects of different modes on the system failure probability are different, the contributions of updating different Kriging models are also different to estimating the system failure probability under RI-HU.In order to pay as little computational cost as possible on the premise of accurately identifying the state of each candidate random sample x∈S,a new system learning function is proposed to improve the efficiency of constructing the system Kriging models under RI-HU, and the advanced AK-MCS method (aAK-MCS) is established to estimate Pand Pefficiently.The proposed system learning function can adaptively select and update the Kriging model currently contributing most to estimating the system failure probability. Thus, the number of model calls required to train the system Kriging models can be reduced significantly compared with the above AK-MCS in Section 3 and the efficiency of estimating the system failure probability under RI-HU can be further improved on the basis of ensuring the accuracy. For the applicability, the proposed method has no limit on the dependency of the failure modes.In fact, the failure modes of the examples, which will be presented in Section 5, are dependent due to the same input variables in the different failure mode performance functions.

4.1. System learning function under RI-HU

For the series system containing m modes under RI-HU, at one random candidate sample point x(x∈S), if there is at least one candidate interval sample (i.e., ∃y∈S) under at least one mode of the system(i.e.,∃k ∈w=｛1，2，...，m｝)satisfying the predicted value g（x，y）≤0 and the U learning function value U（x，y）≥2 simultaneously, it indicates that xhas been accurately identified as a failure sample by the current system Kriging models with a probability not less than 97.7%. Then the Kriging models of all modes don’t need to be updated at xany more. Thus, the maximum of the U learning function values of all modes’ Kriging models g（X，Y）（k=1，2，...，m） at all candidate interval samples y∈S（j=1，2，...，N）should be assigned to the system learning function value at x.Otherwise,in order to find the random sample in Swhose state is most inaccurately identified by the current system Kriging models, the minimum of the U learning function values of all modes’ Kriging models at all candidate interval samples should be assigned to the system learning function value at x.

Based on the above analysis, the system learning function U（x） for estimating the series system failure probability Punder RI-HU is constructed in Eq. (17),

where w=｛1，2，...，m｝ is the set of the labels of all modes in the system.

For one random candidate sample x,it can combine different interval candidate samples with different modes to form N×m combinations totally. As long as the state of at least one combination can be accurately judged as a failure one by the current system Kriging models with a probability greater than the predefined probability (97.7% in this paper),it can be considered that xhas been accurately identified as a failure sample.Thus,the system learning function make sure that xneed not be added to the training sets to update the system Kriging models. For the random samples that have not been accurately identified, Section 4.2 will show how to select the new training sample to update the Kriging model contributing most to estimating the system failure probability.

4.2. Implementation of aAK-MCS for estimating Pf·series and Pf·parallel

On the basis of the proposed system learning function, the aAK-MCS can be established. Taking the series system containing m modes as an example, the detailed steps of the aAK-MCS for estimating Pare illustrated as follows.for estimating the parallel system failure probability Punder RI-HU can be established. For the system containing an arbitrary relationship, it can be seen as the combination of the parallel system and the series system, and the failure probability Pcan be estimated by the boolean operation. For the sake of brevity, these steps for estimating Pand Pare omitted.

5. Examples

In this section, four examples are provided to show the feasibility and advantages of the proposed methods for estimating Por P, and the MCS is applied as the reference method. The error is computed by

5.1. Example 1: a parallel system with three modes

Consider a parallel system consisting three failure modes. The highly nonlinear limit state functions of the three modes are as follows,

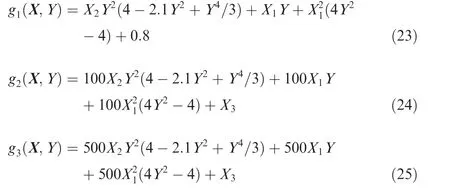
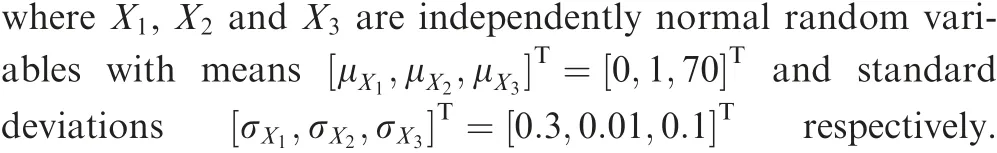
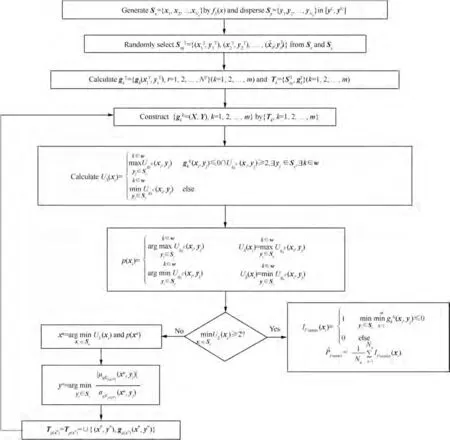
Fig. 1 Flowchart of aAK-MCS for estimating Pf·series under RI-HU.

Table 1 shows that for the parallel system, the system failure probability under RI-HU obtained by the AK-MCS and the aAK-MCS are basically consistent with the reference method. Compared with the MCS, the AK-MCS greatly reduces the number of times for evaluating the system performance functions.On the premise of ensuring the accuracy,the aAK-MCS can further reduces the number of the times for evaluating the system performance functions by using the system learning function to construct the system Kriging models of the limit state surface. In terms of the computational efficiency, the aAK-MCS significantly shortens the runtime for training the system Kriging models compared with the AKMCS.Because the system performance functions are explicitly time-saving, this example can’t reflect the advantage of the proposed methods in terms of the total runtime. But for the implicitly time-consuming performance functions of the complicate engineering structures (this part will be reflected in Example 4),as the number of the times for evaluating the system performance functions is greatly reduced, the total runtime of the AK-MCS and aAK-MCS will be less than the MCS.

Table 1 Results of Example 1.

5.2. Example 2: a bracket of two bars system

This example considers a bracket of two bars system.As Fig.2 shows,bar 1 on the left is always being compressed,while bar 2 on the right may be compressed or tensed as the angle θ of the load changes.If the compressive or tensile stress on any one of the two bars exceeds the yield strength of the material, the bracket of two bars system fails.Thus,it can be seen as a series system containing three failure modes and the corresponding system limit state functions are shown as follows,

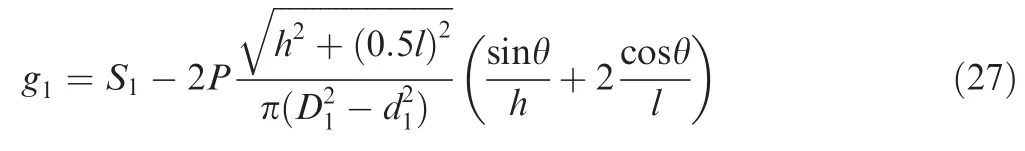
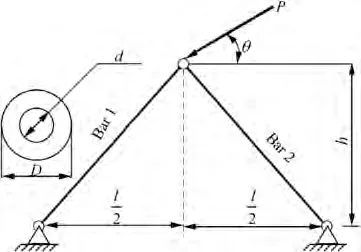
Fig. 2 Bracket of two bars.

Table 3 shows that for the series system, the system failure probability under RI-HU obtained by the AK-MCS and the aAK-MCS are basically similar to that of the reference method. It means that the proposed system learning function and advanced AK-MCS method are suitable for the series system reliability analysis problems. Similar to Example 1, the AK-MCS and the aAK-MCS evaluate the system performance functions for significantly less times than the MCS under the premise of ensuring that the size of the sample pool and the coefficient of variation are the same. Because the system performance functions are explicitly time-saving, this example can’t reflect the advantage of the proposed methods in termsof the total runtime. For the series system under RI-HU, the aAK-MCS is more efficient than the AK-MCS in terms of the number of the times for evaluating the system performance functions and the runtime for training the system Kriging models. Thus, for the implicitly time-consuming performance functions of the complicate engineering structures, the total runtime of the AK-MCS and aAK-MCS is less than the MCS, and the runtime of the aAK-MCS is less than that of AK-MCS.

Table 2 Input variables and their descriptions in Example 2.*

Table 3 Results of Example 2.

5.3. Example 3: an aerospace fuel tank series system

Consider the reliability analysis of an aerospace fuel tank.It is formed by 40 individual boxes with a honeycomb sandwich structure as shown in Fig. 3. The main load on the fuel tank mainly comes from shearing and flexural stress caused by the mass of the fuel and the acceleration of spacecraft. The walls of the fuel tank fail when the isotropic strength (ISO) of the transverse direction is exceeding,the Von Mises(VM)strength is exceeding or the Honeycomb Buckles (HB). Thus, the aerospace fuel tank contains three failure modes forming a series system and the corresponding limit state functions are defined as follows,

The descriptions, the types and distribution parameters of the input variables are shown in Table 4. The series system failure probability is defined in Eq. (37). In this example, the two-dimension interval variables are scattered into N=10×10=100 samples in the interval range. The results of the proposed methods and reference method for estimating Pof Example 3 are shown in Table 5.During the process of the algorithm, the updating times of Kriging models of the three limit state functions in the AK-MCS and aAK-MCS are shown in Table 6.

5.4. Example 4: an aircraft undercarriage system

This example considers a reliability analysis model of an Aircraft Undercarriage System (AUS).Fig. 4 shows the parts schematic diagram of the AUS, where A-E are hinge points and F is joint point. The main running procedures of the AUS can be summarized as the retracting procedure and the releasing procedure: (A) During the retracting procedure, the landing gear is retracted to the aircraft,then the pillar is taken back to the uplock location by the actuator-cylinder and the hinges are locked. (B) During the releasing procedure, the actuator-cylinder unlocks the hinges and the landing gear is released by the gravity. The pillar is released to the downlock location by the and the hinges are locked.

In this example, the input variables of the AUS reliability analysis model and their descriptions are shown in Table 7.

Three failure modes of the AUS are constructed by considering its dynamic properties:

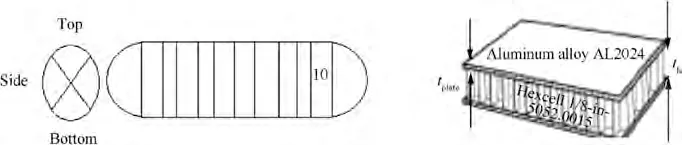
Fig. 3 Schematic diagram of tank and material.

Table 4 Types and distribution parameters of input variables in Example 3.

Table 5 Results of Example 3.

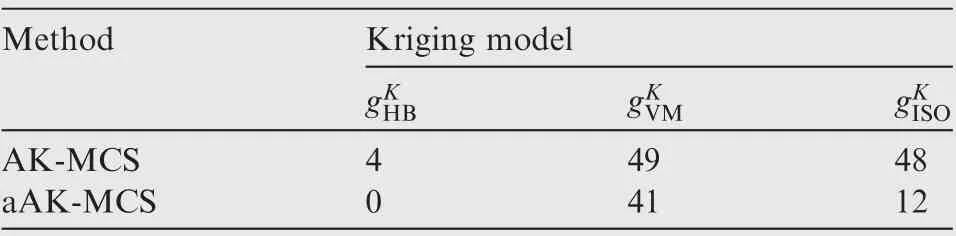
Table 6 Updating times of system Kriging models in Example 3.

(1) During the retracting procedure,if the load on the AUS exceeds the driving power produced by the power plant,the landing gear cannot get back to the aircraft.According to this situation, the limit state function of this failure mode can be formulated as follows,F=5.9×10（N） is the driving power produced by the power plant and F（X，Y）denotes the load on the AUS during the retracting procedure.

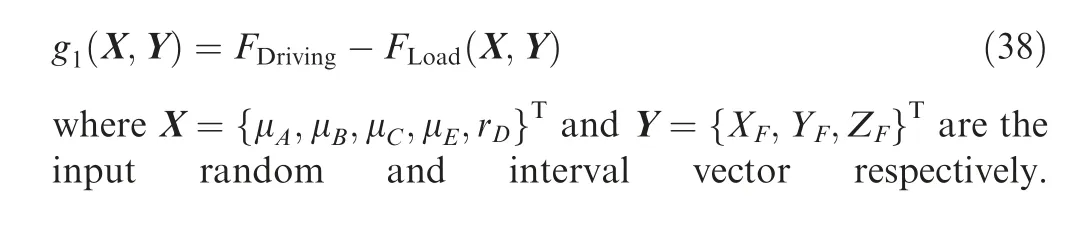
Fig. 4 Parts schematic diagram of AUS.

(2) During the retracting procedure, the landing gear can not get to the uplock location in the prescribed time,which means it cannot be locked normally. The limit state function corresponding to this failure mode can be formulated as follows,

where β=94.2600is the dihedral angle from the complete retracting condition to the complete releasing condition of the landing gear, which is shown in Fig. 6(a). The real maximum rotating angle of the landing gear between these two conditions is β（X，Y）as shown in Fig.6(b).θ=0.3085denotes the threshold of the angle deviation allowed.

As long as one of the above three modes fails, the aircraft undercarriage system will fail. Thus, the three modes form a series system and the corresponding system failure probability is defined by Eq.(41).In this work,the values of implicit functions F（X，Y）, α（X，Y） and β（X，Y） are obtained by the dynamic analysis through ADAMS software. The results of the proposed methods and reference method for estimating Pof Example 4 are shown in Table 8.

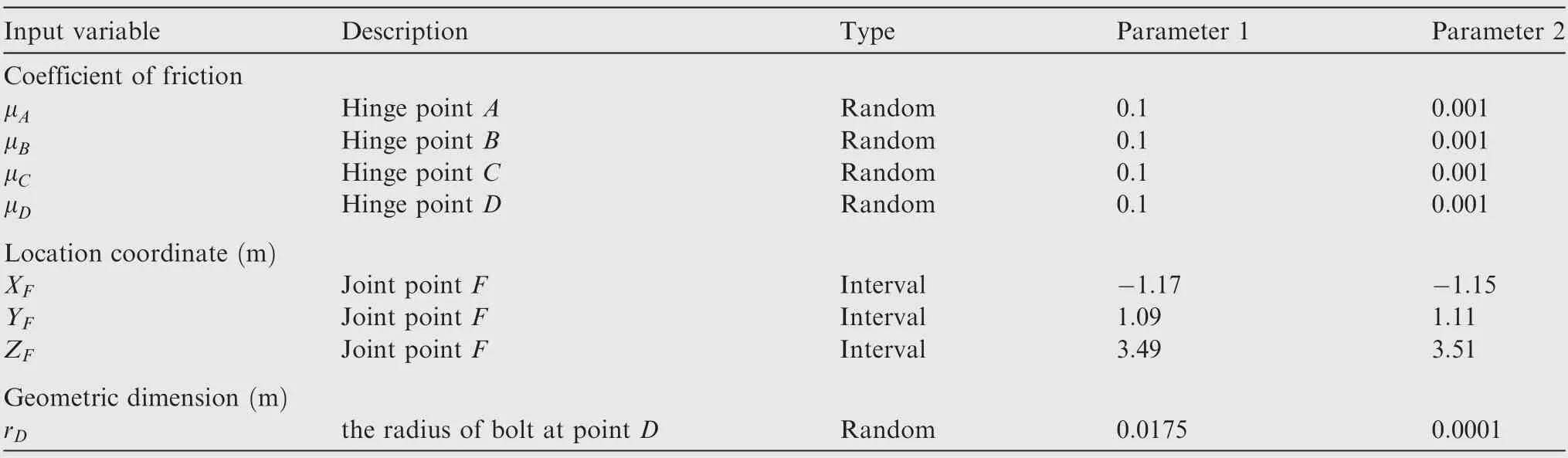
Table 7 Input variables and their descriptions in Example 4.

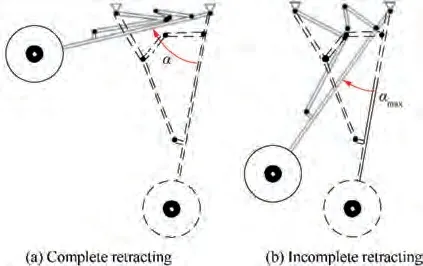
Fig. 5 A simple sketch of the retracting procedure.

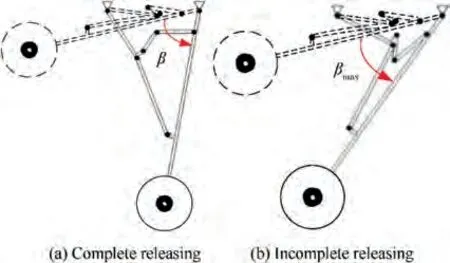
Fig. 6 A simple sketch of releasing procedure.

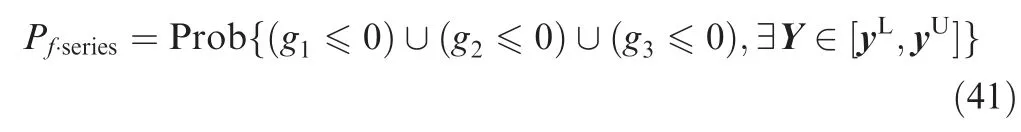
This example shows that the proposed methods are also suitable for system reliability analysis of the engineering problems under RI-HU. The AK-MCS and aAK-MCS are much more efficient than the MCS in terms of the total runtime because of the time-consuming analysis model in this example.Compared with the AK-MCS, the aAK-MCS can further reduce the runtime for evaluating the system performance functions and training the system Kriging models.

5.5. Example 5: a simplified wing box structural model

Consider a simplified wing structure of a nine-box section shown in Fig.7(a).It is a plate-bar structure consisting 64 bars and 42 plates. The lengths of the bars in the y, x and z directions are L=L, L=2L and L=3L respectively. The sectional area of all the bars is denoted by A, the thickness of all the plates is represented by TH, E is the elastic modulus of all bars and plates, and P is the load in the y direction.The Poisson’s ratio is 0.3. The types and distribution parameters of the above input variables are shown in Table 9.

The nine-box wing structure fails when the maximum displacement in y direction is exceeding, the stress in any one of the bars in z direction is exceeding or the shearing stress in any one of the plates is exceeding.Thus,it can be seen as a series system containing three failure modes and the corresponding system limit state functions are shown as follows,

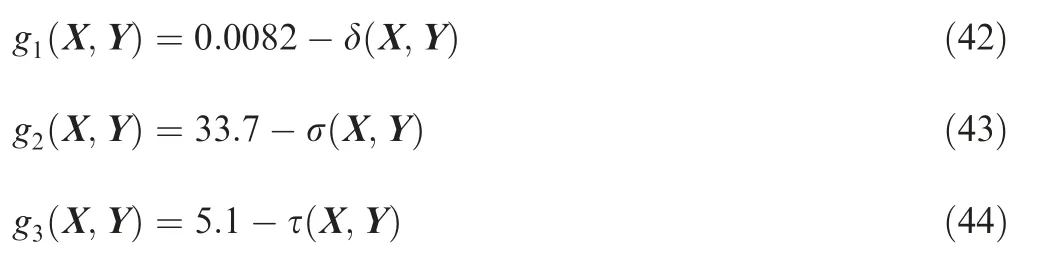
where δ（X，Y）(m)is the maximum displacement in y direction,σ（X，Y）(MPa)is the maximum stress of the bars in z direction and τ（X，Y） (MPa) is the maximum shearing stress of the plates. They are implicit functions of the input variables, and can be obtained by the finite element analysis through ANSYS software, and the schematic diagram of finite element analysisare shown in Fig. 7(b)-(d) respectively. The series system failure probability is defined in Eq. (45).

Table 8 Results of Example 4.

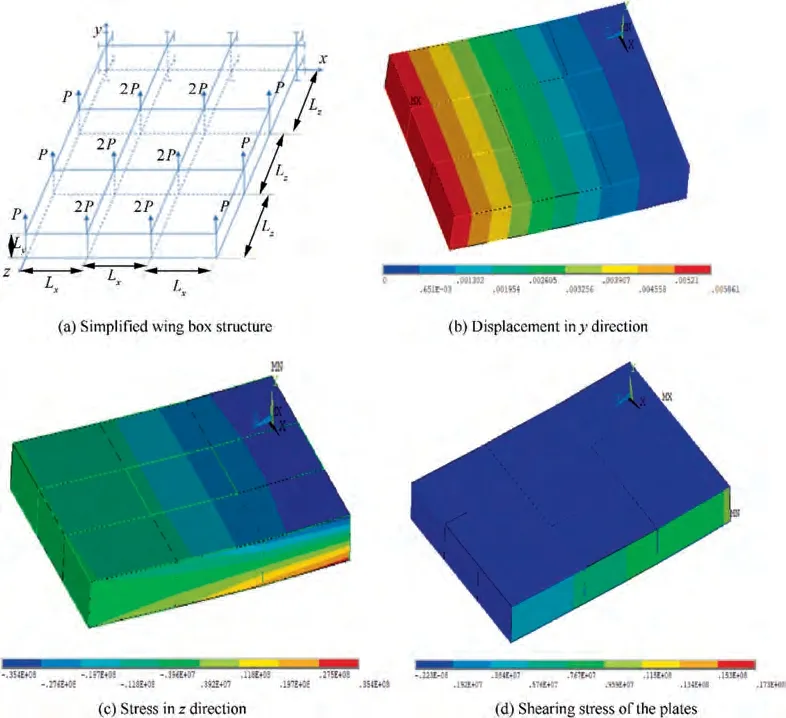
Fig. 7 Wing box structure.

Table 9 Types and distribution parameters of input variables in Example 5.

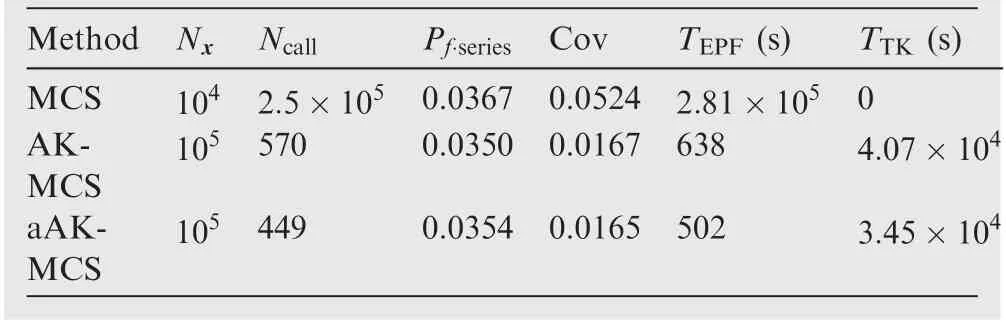
Table 10 Results of Example 5.

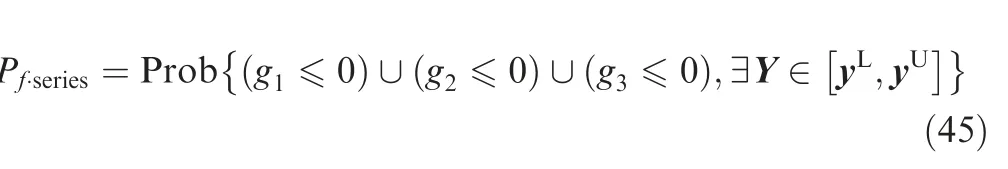
The results of the proposed methods and reference method for estimating Pof Example 5 are shown in Table 10.The conclusions drawn in this actual practical example are similar as those of Example 4.

6. Conclusion

(1) Aiming at the multi-mode system reliability analysis under the Random and Interval Hybrid Uncertainty(RI-HU), a strategy combining numerical simulation with the adaptive Kriging (AK-MCS) is proposed to estimate the upper bound of the failure probability of the system.

(2) The proposed AK-MCS constructs the Kriging model of each failure mode’s limit state function to estimate the failure probability Por Pof series system or parallel system. The number of times for evaluating the model in the AK-MCS is much less than that in the MCS method because the training set size of the system Kriging models is much smaller than the candidate sample pool size of the MCS.

(3) The AK-MCS requires that each Kriging model can accurately estimate the failure probability of the corresponding single mode, however, since the effects of different modes on the system failure probability are different,the contributions of updating different Kriging models to estimating the system failure probability under RI-HU are different too. The AK-MCS which indiscriminately constructs and updates the Kriging models of all modes may lead to unnecessary computational cost. For the deficiency of the AK-MCS in estimating the system failure probability under RU-HU, a system learning function and an advanced adaptive Kriging model combined with numerical simulation method (aAK-MCS) are proposed for estimating the system failure probability.

(4) The proposed system learning function can adaptively select and update the Kriging model currently contributing most to estimating the system failure probability.On the premise of correctly identifying the state of each random candidate sample, the updating process of the secondary Kriging models is avoided. Thus, the computational efficiency is further improved.

(5) Three numerical examples and two practical engineering examples all demonstrate the efficiency and accuracy of the proposed methods. In addition, compared with the AK-MCS, the aAK-MCS can further improve the computational efficiency for the complicated engineering structures.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

Supplementary data to this article can be found online at https://doi.org/10.1016/j.cja.2021.08.017.