自动化码头多级作业超网络延误传导特性研究

许波桅，王玲玲，李军军

(上海海事大学，a.物流科学与工程研究院；b.商船学院，上海 201306)

0 引言

自动化码头作为连接水陆集装箱运输的重要物流节点，其作业效率直接影响着集装箱运输体系的流畅程度。整个自动化码头包括4个区域，即岸边区域、运输区域、堆场区域以及陆侧区域，主要进行岸桥装卸、场内AGV(Automated Guided Vehicle)运输、堆场内场桥装卸以及外集卡提箱送箱等多级作业。通常情况下，船公司在提供船期预报后，由港务局提供月度船期计划，码头据此安排泊位计划、岸桥数量、AGV数量及堆场作业机械等。自动化码头多资源多环节的特点使得码头多级作业之间相互联系，相互影响，呈现网络化的特点。

因而，在码头运营过程中，诸如，船舶延误、恶劣天气及AGV 行驶冲突等各类不确定事件的出现，不仅会导致当前作业中断，产生延误，甚至这种延误还会在码头的上、下级作业之间传导，形成“连锁”效应。并且，随着时间的推移，由延误导致的时间成本增加，设备资源闲置，集装箱滞留增多，交货延迟及运营混乱等供应链管理问题会越来越严重，影响自动化码头作业的生产效率。目前，多数学者在研究这一问题时，主要是从计划排程和调度优化等角度进行解决[1-2]。然而，自动化码头是一个复杂系统，各级作业间相互关联，延误问题会在整个系统中被放大并扩散，单从某一环节入手进行计划与调度并不能很好的分析与描述码头整体受到的影响。现有研究鲜有从网络视角出发，讨论和模拟延误在整个多级作业网络中的影响。

目前，借助复杂网络理论研究交通网络传导问题已取得大量成果。胡立伟等[3]构建城市交通拥塞因子风险复杂网络，研究城市交通拥塞因子风险传播特性。戈佳威等[4]利用传播动力学理论研究世界集装箱海运网络港口延误问题，识别延误在集装箱海运网络中的传播特性。XU B.等[5]以码头设施为节点，以不确定时间为超边，利用超网络理论，研究不确定事件在自动化码头多级作业之间的传播影响。考虑到不确定事件存在的客观性和自动化码头多级作业环境的复杂性，本文将超网络理论引入到自动化码头多级作业中，以码头的设备资源为节点，码头装卸作业任务为超边，构建自动化码头多级作业超网络。通过特征路径长度和聚类系数等网络结构特性，分析不确定事件带来的作业延误在自动化码头多级作业超网络中的传导情况，主要包括：传导速度、传导范围以及传导能力3方面，并通过仿真分析的结果给出码头运营的对策建议。

1 自动化码头多级作业超网络模型及其适用性

1.1 问题分析

如图1所示，码头多级作业环环交互，紧密联系。船舶装卸作业是码头日常的主要作业，对于卸船作业来说，船舶在到港后由岸桥进行卸船，再由AGV 将其运输至堆场，由场桥吊至合适贝位进行存储，装船作业则反之。在实际作业中由于各类突发事件的出现，会导致部分作业中断，中断意味着带来作业延误，并且由于作业之间交互联系，其他环节也会受到影响。例如，假设运输过程中的AGV 出现故障，并且该故障没有在既定的时间内被修复，此时，该AGV 的运输作业就发生了延误。称这类受到不确定事件影响产生延误的设备为“故障节点”，由于该AGV 无法按时到达目的地，导致岸桥设备、场桥设备等“正常节点”的作业等待，产生进一步的延误。随着时间的推移，会影响到更多节点。

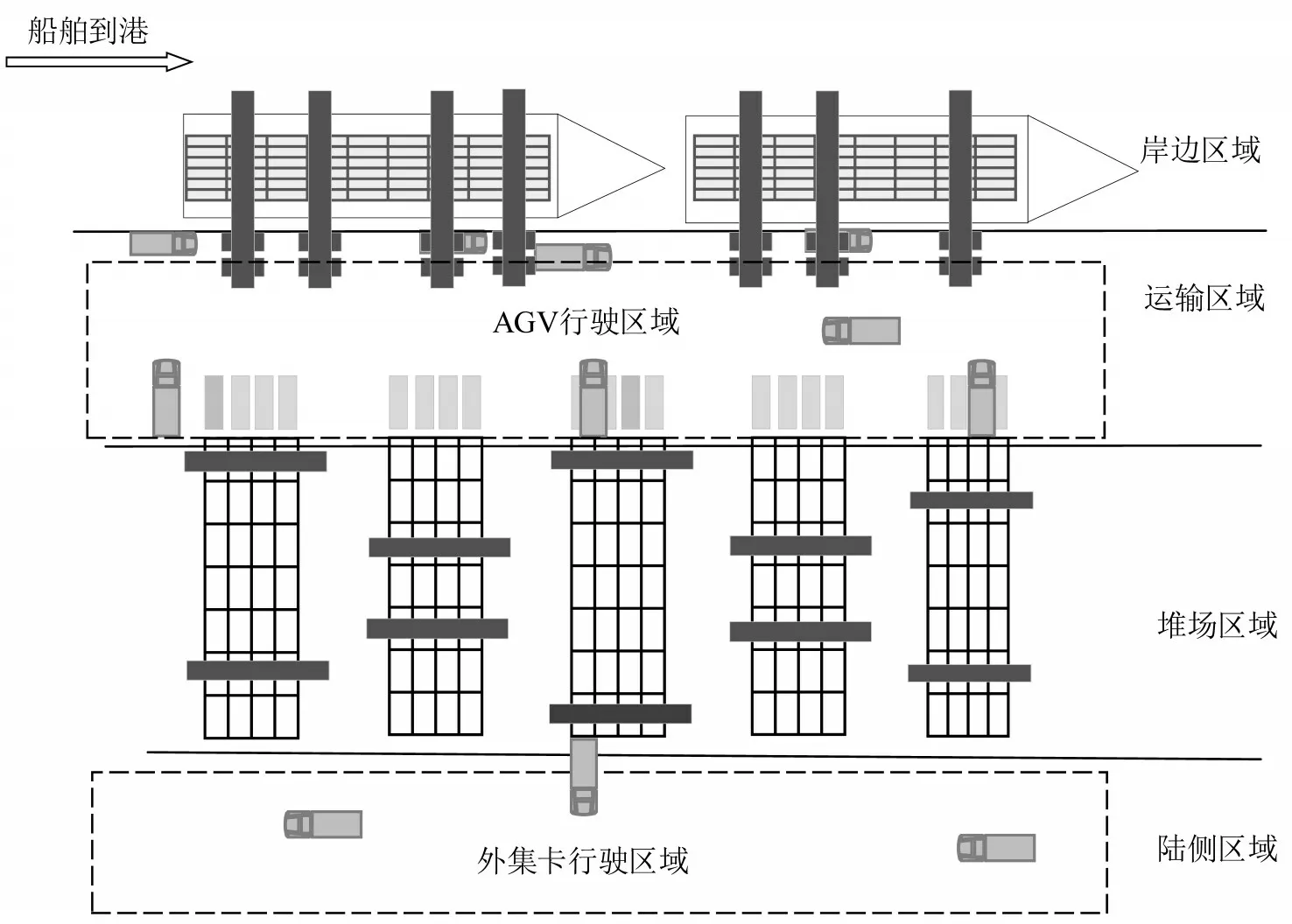
图1 自动化码头多级作业布局Fig.1 Layout of multilevel handlings of automated container terminal

自动化码头是一个多资源多环节的复杂系统，在不确定事件发生时，对码头作业的影响会涉及多个方面，本文仅考虑不确定事件对码头多级作业造成“时空异步”时所产生的延误影响。伴随着自动化码头内部因素和外部环境因素的多重作用，延误虽然已知会随着设备之间的相互联系进行传导，但是传导速度和传导范围不尽相同，因此，本文尝试构建一个多级作业超网络，通过分析其网络结构特性，研究由不确定事件带来的延误在网络中的传导速度、传导范围以及传导能力的变化。

1.2 自动化码头多级作业超网络模型

自动化码头多级作业是一个复杂系统，各级作业间相互关联，延误问题会在整个系统中被放大并扩散，单从某一环节入手进行计划与调度并不能很好地分析与描述码头整体受到的影响。而超网络理论能够简明和准确地刻画各类节点之间的复杂关系和现实网络的多元结构，符合描述自动化码头多级作业特征。为此，本文以自动化码头的作业设备为节点，以装卸作业任务为超边，构建自动化码头多级作业超网络，并通过在网络中添加“故障节点”研究不确定事件带来的延误在多级作业超网络中的传导速度、传导范围以及传导能力的变化。

(1)假设条件

①以自动化码头内AGV、岸桥及场桥等作业设备为节点，以作业任务为超边。当任务结束时，任务中所包含的节点释放，且任务中的“故障节点”在下次进入网络中默认为已被修复的“正常节点”；新节点是当新作业任务出现时，新加入到网络中的部分。

②频繁出现在多个作业任务中的节点，发生延误时节点的传导概率越大。

③每个时间步长里增加一条超边。

④新超边中包含的新节点和旧节点数量由泊松概率给出[6-7]。泊松分布适用于描述单位时间内随机事件发生的个数。对于自动化码头，每次完成一项装卸任务所涉及的设备个数并不是固定不变的，根据每次任务装卸量的不同，在实际安排作业过程中，涉及的节点会有变化。这意味着在本文所构建的自动化码头多级作业超网络中，当新增一条超边时，其中的新节点和包含的旧节点是不确定的，而泊松分布的特点与这一属性相符合。

(2)符号说明

S(t)——所有正常节点的集合；

St——t时刻正常节点的比例，即S态(正常状态)密度，

s(t)——正常节点数量；

I(t)——所有故障节点的集合；

It——t时刻故障节点的比例，即I态(故障状态)密度，

i(t)——故障节点数量；

i(0)——网络中初始故障节点数；

N——网络总节点数；

β——传导概率，即故障节点“感染”健康节点的速率；

γ——修复概率，即故障节点被检测维护并再次成为健康节点的效率高低；

ki——节点v的节点超度，即包含节点v的作业任务数；

ei——节点v与其邻居节点实际相连的边数；

Ei——第i条超边；

m——初始化时超边E1包含的节点数。

(3)模型构建

具体步骤如下：

Step 1 初始化。假设初始化时m个节点和包含着m个节点的1条超边E1。

Step 2 超边增长。每个时间步长增加1 条超边，包含n个新节点，并与旧超边存在m0个节点重合，即新超边中包含n个新节点和m0个旧节点。

Step 3 网络形成。判断所有任务是否全部结束，若没有返回Step 2；否则，网络形成。

不确定事件的出现对自动化码头多级作业网络的延误主要体现在Step 2，诸如，设备故障、恶劣的天气条件、装卸量增加及船舶延期等不确定事件的出现会直接、间接影响到码头内的多个节点。当网络中出现“故障节点”后，“故障节点”以概率β影响“正常节点”作业，即“正常节点”在受“感染”后成为“故障节点”，网络内“故障节点”数量增加；另一方面，“故障节点”以概率γ被恢复。且随着时间增加，一部分作业任务完成，此时，该超边会退出网络，超边中原有的节点也会重新释放，等待跟随新的超边再次进入网络。

初始时刻m=4，β=0.2，γ=0.1 时的超网络演化模型如图2所示。

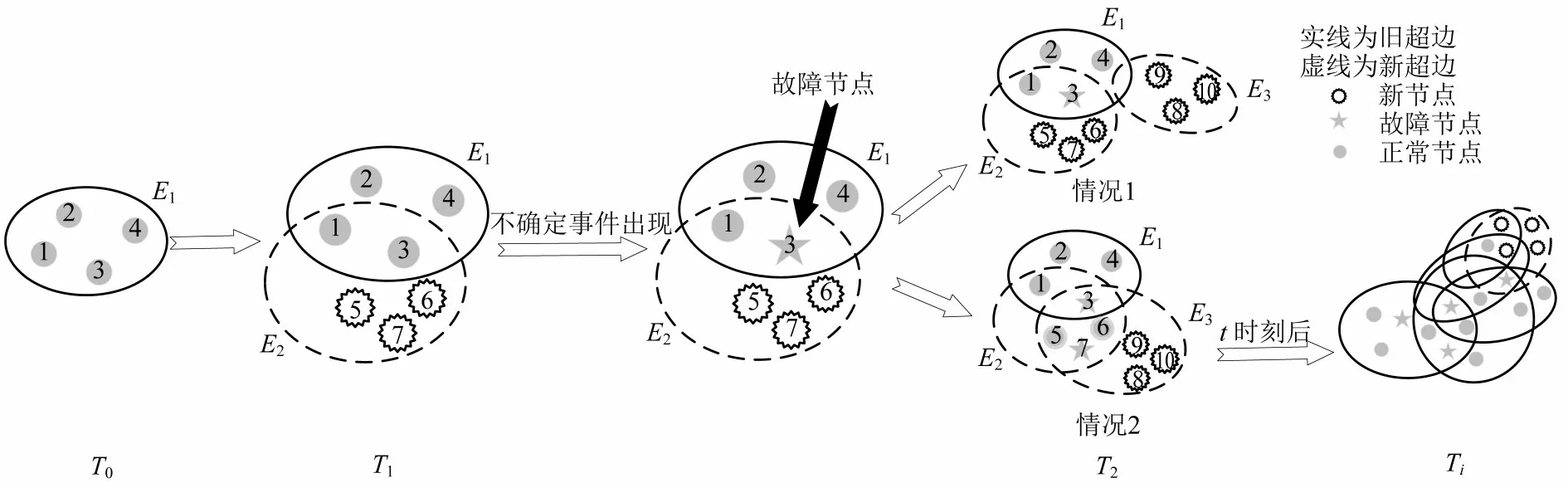
图2 多级作业超网络模型演化示意Fig.2 Schematic diagram of evolution of multilevel handlings hypernetwork model

图2中，在T0时刻，网络中只有1 条超边E1并包含了4个节点，T2时刻新超边E2加入，产生新节点V5、V6、V7。由于某一不确定事件的出现导致节点V3发生延误，成为“故障节点”。T2时刻新超边E3增加，若E3中的作业不涉及节点V3，即E3中不包括“故障节点”，则传导暂停，如T2时刻的情况1 所示；否则，传导继续，如T2时刻的情况2 所示。此时，V3以概率β感染了V7，使得节点V7成为“故障节点”；另一方面，码头管理者会以概率γ对“故障节点”进行修复，经过多次重复至所有任务结束之后，最终，形成Ti时刻的超网络。

1.3 适用性分析

自动化码头多级作业超网络是由多个网络节点、网络连接边及外部环境所构成的复杂系统，具有复杂性和不确定性等特点。由于自动化码头各设备节点与复杂的码头作业系统相互关联，延误问题会在这些系统中被放大并扩散，甚至会造成对整个超网络的影响。延误在多级作业超网络中的传播行为与传播动力学在传导机理和传导对象等方面极为相似。

(1)传导机理的相似性

对于自动化码头多级作业来说，各项装卸任务会提前进行计划安排。然而，自动化码头多级作业存在固有的不确定性。例如，AGV 设备的故障会导致岸桥卸船作业的延误，从而导致后面装船作业的延误。当延误发生时，延误首先会向其延误源节点的相邻节点进行扩散，再依次向其他相关节点蔓延。这与交通网络中拥堵蔓延和社交网络中谣言传播十分相似。

(2)传导对象的相似性

以装卸作业设备为自动化码头多级作业网络中的节点。在实际作业中，由于码头装卸作业的繁重，各台设备每天需要参与多项装卸任务，即各节点是相互联系的独立主体。此外，对于恶劣天气和设备故障等“感染源”，节点对其往往没有“免疫”功能，会再次受到“感染”。同时，考虑到不同设备的性能、体积及维护周期等因素，自动化码头多级作业超网络各节点具备不同的延误传播能力和修复能力。根据传播动力学模型的分类，相比易感-传染(SI)、易感-传染-免疫(SIR)及易感-传染-免疫-易感(SIRS)模型，自动化码头多级作业延误传导更适合采用易感-传染-易感模型(SIS 模型)进行评估。

2 自动化码头多级作业超网络结构特征分析

当前，应用超网络理论的文献中，所构建的超网络模型度分布大多数符合幂律分布，即符合无标度网络特征。在无标度网络中，大部分节点度会很小，只有小部分节点的度值很大。例如，在科研合作网络中这代表着知名度更高的学者往往论文数量会更多，在自动化码头交通路网中，这表示存在小部分节点在网络中出现的频率非常高。例如，AGV 水平运输是衔接岸桥作业和场桥作业的中转区域，在自动化码头多级作业中的地位无疑是非常重要的，但是，对于岸桥和场桥等装卸设备来说，也同样移动了多次。考虑到码头实际生产中各环节作业之间的紧密性，即各节点之间表现为较短的特征路径长度，且由于网络中不再存在优先连接，小世界网络的特性会表现得更加明显。因此，本文通过特征路径长度[8]和聚类系数[9]等网络拓扑指标分析所构建的自动化码头多级作业网络的结构特征。

2.1 特征路径长度

假设t时刻增加新超边时，“故障节点”会以概率β感染“正常节点”，则此时“故障节点”会以βs(t)的速度与网路中的节点产生联系，s(t)表示t时刻网络中正常节点的数量，它等于网络中总节点数量减去故障节点的数量，故障节点数量为i(t)，N为网络中的总节点数，新超边以概率p与旧超边产生邻接，则修正后的特征路径表示为

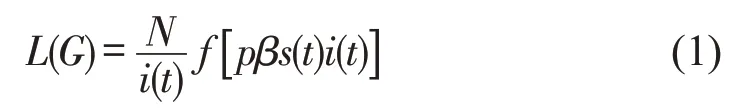
式中：f[pβs(t)i(t)]——一个通用的标度函数，满足

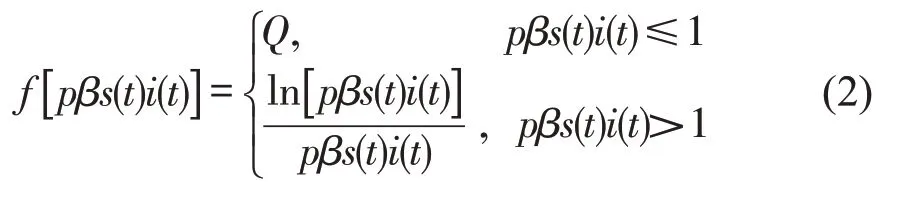
式中：Q——常数。

2.2 聚类系数

聚类系数表示网络中节点之间的聚集程度，已成为表征复杂网络拓扑结构的全局标准参数之一。节点v的聚类系数越大，节点v与其他节点间的紧密程度越大，说明其传导路径越多，则传导范围越广，因此，聚类系数是描述网络结构特征的重要指标之一。网络整体的聚类系数C一般表示为

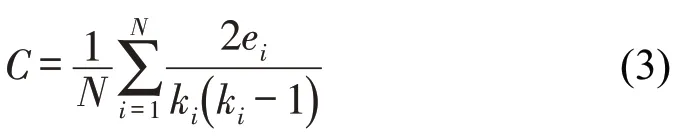
通常C的范围在0～1之间，当C=0 时，表明所有节点均为孤立节点，各节点之间并不存在传导条件；当C=1 时，表明网络中任意两个节点都存在直接联系。但是，这两种情况都不符合本文所构建的自动化码头多级作业超网络模型。本文所构建的自动化码头多级作业超网络模型既不是完全随机的，也不是完全规则的，符合小世界网络特性。因此，为能将式(3)用传导概率表示并简化运算，修正后的集聚系数为

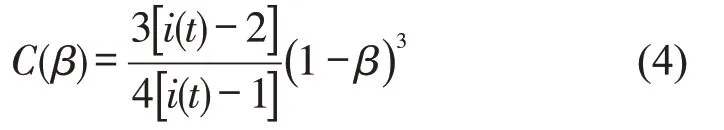
2.3 传导能力

网络的传导能力，即故障节点的有效传播率，根据传播动力学文献[11]模型的特点，延误在自动化码头多级作业中的传导问题适用于SIS 模型求解。即健康节点以一定概率受感染成为故障节点后，会以某一概率重新恢复为健康节点。SIS 动力学方程为

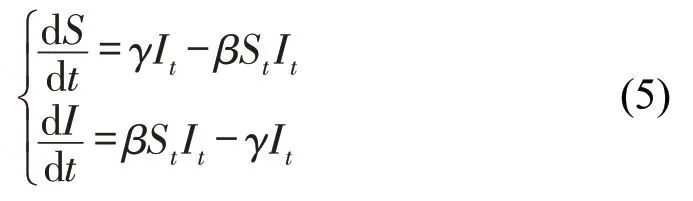
推导后，得方程解为

在实际网络中，当网络节点由于某些因素相互作用，形成传导行为时，可以用传染病模型进行仿真模拟。不同的是，由于传染病模型是连续函数，在运用到实际网络中时需要离散化处理，以贴近实际情况，因此，模型可以改为

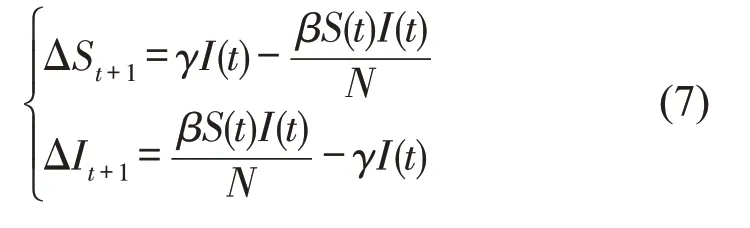
3 延误在多级作业超网络中的传导特征分析

有关“故障节点”带来的延误在多级作业超网络中的传导特征分析，本文主要基于所构建的自动化码头多级作业超网络结构特征，运用MATLAB进行数值模拟与研究，分3种情况展开：第1种情况是数值模拟特征路径长度L(G)与相关变量之间的关系，以分析传导速度的变化情况；第2 种情况是数值模拟聚类系数C与相关变量之间的关系，以分析传导范围的变化情况；第3种情况是数值模拟传导能力相关变量之间的关系，以分析传导能力的变化情况。

以自动化码头实际运作情况为依据校准SIS模型的重要参数：网络总节点数、传导概率、初始故障节点数以及修复概率。首先，根据自动化码头的设施、设备数量规模不同，可分为大规模和小规模的情况。例如，厦门远海自动化码头目前配备3台自动化双小车岸桥、16台场桥、18台AGV和8台自动化集装箱转运平台，共45台设备；洋山四期码头目前已有16 台桥吊、88 台轨道吊和80 台自动导引车全部投入使用，共184 台设备。因此，在进行传导速度分析时，为表现不同节点数量下传导速度的变化，在网络总节点数N分别为50，100，200时，对特征路径长度L(G)与传导概率β的变化关系进行仿真。

其次，考虑到自动化码头实际作业中，设备的传导概率受多方面因素影响，因此，将传导概率β变量设置为[0,1]，初始故障节点i(0)的范围设置为[0,m](m为初始化时超边E1包含的节点数)，以观察不同传导概率下不同初始故障节点时的传导情况。延误的发生也与修复概率γ和传导概率β有关，当γ＞β时，延误不再随着故障节点传导。因此，本文将修复概率γ的范围设置为[0,β]。

3.1 传导速度分析

特征路径长度L(G)随网络总节点数N及故障节点数量i(t)的变化如图3所示，特征路径长度L(G)越小，即不同节点之间能够通过更短的路径产生联系，延误的传导速度也更快。

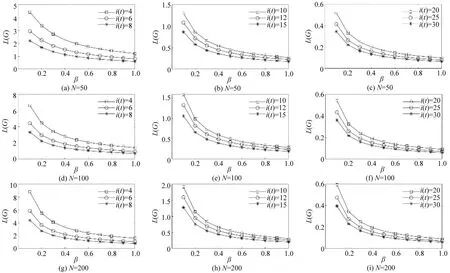
图3 特征路径长度L(G)随网络总节点数N 及故障节点数量i(t)的变化Fig.3 Change of characteristic path length with total number of network nodes and number of fault nodes

由图3可知，当故障节点数量i(t)不变时，随着网络总节点数N的增加，特征路径长度L(G)曲线逐渐向右上方移动，即特征路径长度L(G)随着网络总节点数N的不断增加而增加，特征路径长度L(G)不断增大，不同的两个节点之间需要通过更长的路径才能产生联系，传导速度减缓，说明传导速度与网络总节点数N之间存在负相关关系。

同时，故障节点数量i(t)不同对网络的特征路径长度L(G)的变化也存在着影响。在网络总节点数N不变的情况下，随着故障节点数量i(t)的增加，特征路径长度L(G)逐渐变小，即不同的两个节点之间通过较短的路径就能产生联系，传导速度增加。说明传导速度与故障节点数量i(t)之间存在正相关关系。

通过推导验证上述结论的有效性。

令i(t)=it，s(t)=st，由式(1)和式(2)得

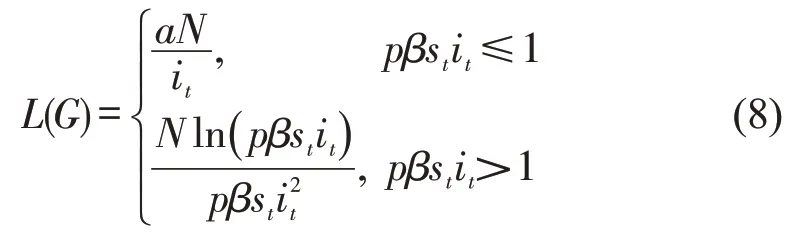
式中：a——一个常数(a＞0)。

当pβstit≤1时，有

当pβstit＞1时，有

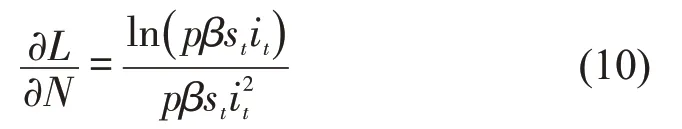
由式(9)和式(10)可知，无论是pβstit≤1 还是pβstit＞1 的情况，恒成立，即特征路径长度L(G)随网络总节点数N的增加而增加。

同样地，当pβstit≤1时，有

当pβstit＞1时，有

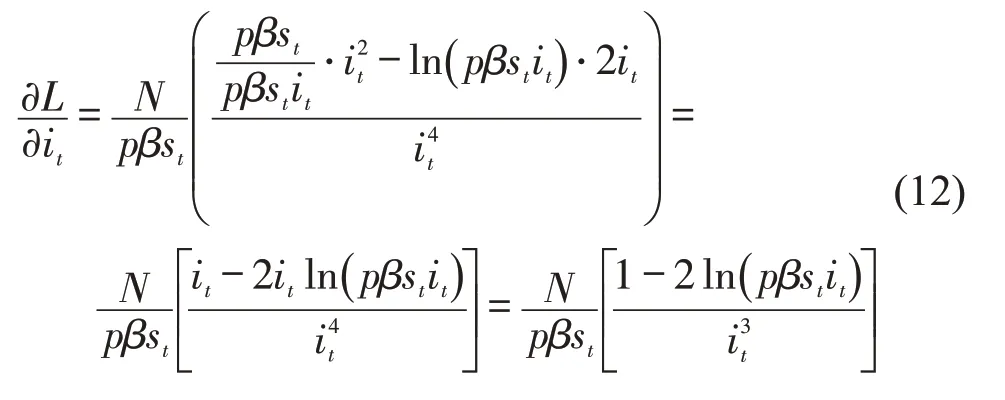
对于式(11)和式(12)，在网络总节点数N取100的情况下，当设置传导概率β依次为0.15，0.20，0.30 时，的变化情况，即L′(G)受故障节点数量i(t)的影响情况如图4所示。

图4显示，推导后的结果始终小于0(无限接近0，但始终小于0)，说明特征路径长度L(G)始终随着故障节点数量i(t)单调递减。验证了特征路径长度L(G)随故障节点数量i(t)增加而减小的结论。

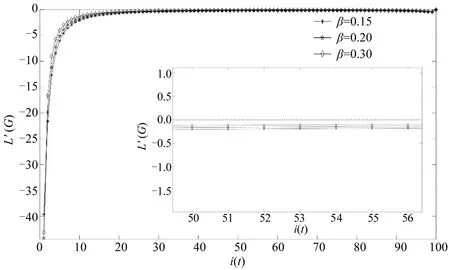
图4 N=100 时L′(G)随故障节点数量i(t)的变化趋势Fig.4 Variation trend of L′(G)with number of fault nodes i(t)when N=100

对于码头管理者来说，通过增加设备，提高现代化水平，应对急剧变化的自动化码头作业环境，构建完整的作业系统体系，在延误发生时，合理调配空闲中的设备资源，将故障节点抽离出网络，可以有效地控制延误传导的速度，提高作业效率。

3.2 传导广度分析

聚类系数表示网络中各节点间的紧密程度，聚类系数越大，网络内部节点间的联系越紧密，故障节点在网络中传导的范围越广。根据式(4)，对聚类系数C与传导概率β以及故障节点数量i(t)之间的关系进行仿真，仿真结果如图5所示。

由图5可知，聚类系数C随故障节点数量i(t)的增加而逐渐增加，随传导概率β的增加而减小。即网络中的故障节点数量i(t)较大时会扩大延误风险的传导广度，而过高的传导概率会缩小传导范围。下面通过推导验证上述结论的有效性。

图5 聚类系数C 随传导概率β 和故障节点数量i(t)的变化趋势Fig.5 Variation trend of clustering coefficient with propagation probability and number of fault nodes

对于式(4)，令i(t)=it，可得

分别对β与it进行微分，结果为

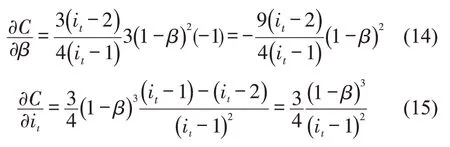
根据推导结果显示，当it＞2 时，，聚类系数C与传导概率β呈负相关。对于，不论it与β如何取值，总是成立，因此，聚类系数C与故障节点数量i(t)呈正相关。随着故障节点数量i(t)的增加，更多的故障节点会将延误传导至与它们存在邻接关系的正常节点，网络的传导范围与传导广度随之扩大。而当传导概率β足够大时，故障节点的传导风险过高，该节点与其他节点的联系会被降低，网络的传导广度随之减小。

当传导概率β增加时，较低的聚类系数会抑制感染密度的增加。这是由于网络中节点之间的内部连接限制了传导扩散的过程，低聚类特性会抑制故障节点的传导扩散。而随着传导概率逐渐增加，网络中初始时刻的故障节点个数随之增加，更多的正常节点将被影响。在这个过程中，虽然低聚类系数可以抑制传导扩散，但是，由于被影响的正常节点数量在不断扩大，单位时间内受感染的正常节点数量(故障节点的有效接触率)增加，因此，网络的低聚类特性对延误传导的抑制作用会被削弱。传导概率β与感染密度的变化如图6所示。表中数据为设置故障节点数量为6和15的情况下，传导概率的变化对聚类系数的影响，进一步地观察聚类特性对感染密度地影响。

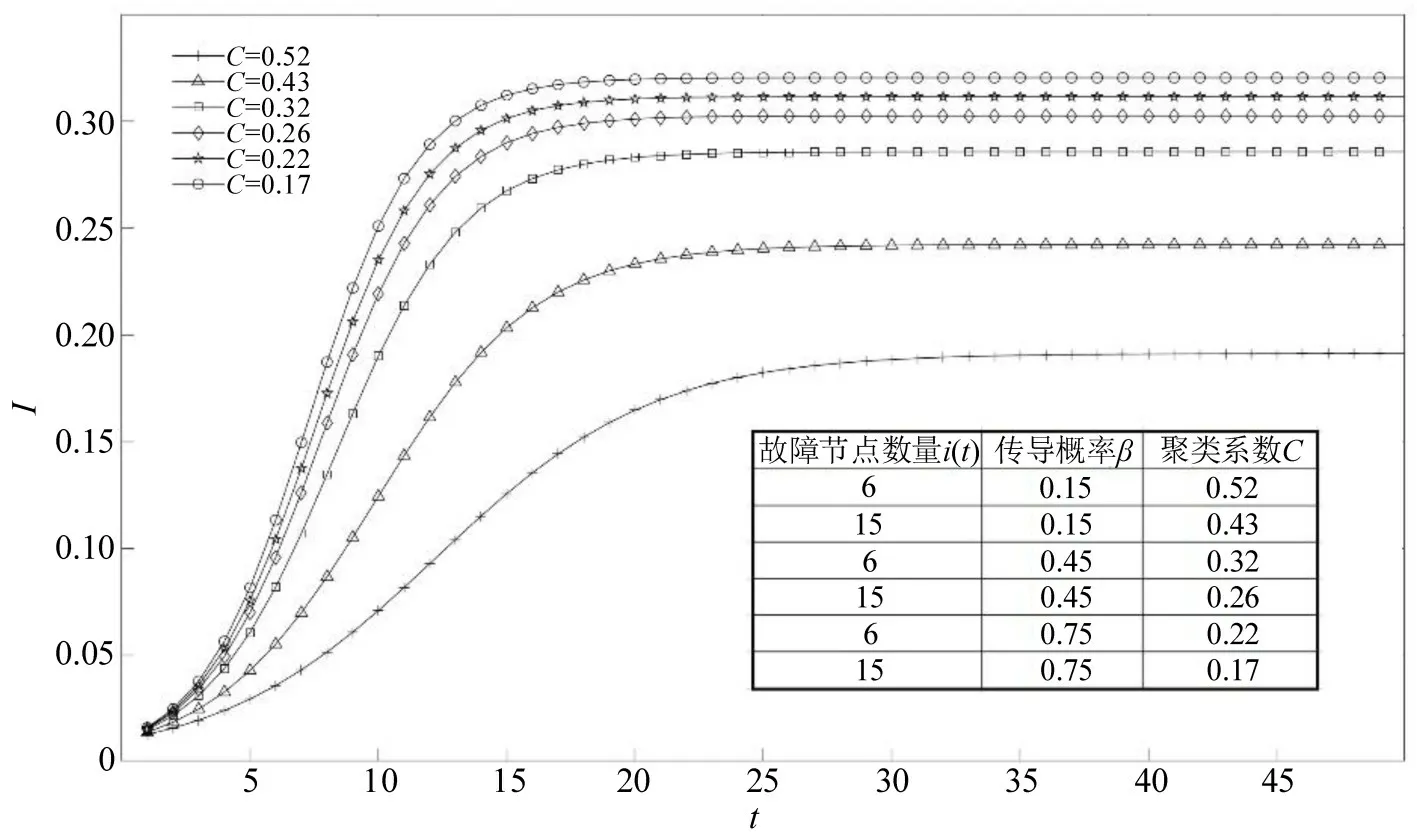
图6 传导概率β 与感染密度的变化情况Fig.6 Changes of propagation probability and infection density

这种变化有力地表现在自动化码头作业中，由于各环节作业的紧密联系，能够帮助码头作业更加快捷高效地完成，但是当出现不确定事件时，却也会加快不确定事件所导致的延误在码头作业中的扩散和传导。对于码头管理者来说，可以通过加强信息共享和信息传输的水平，提高决策水平。当作业中出现故障节点时，通过有效的信息传输与共享，建立新的联系，扩大网络整体的协同度，降低故障节点的聚类特性，缩小延误的传导范围。

3.3 传导能力分析

本文在构建自动化码头多级作业超网络过程中结合了传播动力学的相关理论，为进一步讨论其他相关因素对延误在自动化码头多级作业网络传导中可能存在的影响，接下来对初始故障节点数量i(0)、修复概率γ及超边数量Ei分别进行具体分析。

由式(6)可得，传导过程受初始故障节点数量i(0)、修复概率γ及总节点数量N的影响。通过不同的变量控制，进行SIS 模拟，探讨自动化码头作业网络的传导特性。不同传导概率下不同初始故障节点时的传导情况如图7所示。

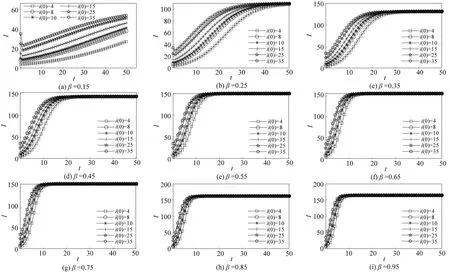
图7 不同传导概率下不同初始故障节点时的传导情况Fig.7 Propagation conditions with different number of initial fault nodes under different propagation probabilities

由图7可知，在修复概率γ保持不变时，随着初始故障节点数量i(0)的逐渐增加，受感染的节点数量越来越多，传导能力越来越强，完成SIS 传播过程的时间越短。当β≤0.45 时呈显著变化，β∈[0.45,0.65]变化微弱，β≥0.75 时并不明显。因此，不同故障节点数量为初始节点时的传导能力与传导概率呈正相关，且在传导概率较小时区分度更高。

修复概率γ与传导能力的关系如图8所示。由图8可知，修复概率γ较小时，故障节点在网络中的传导能力更强。当修复概率γ逐渐增加时，故障节点的传导能力会得到抑制。且这种抑制作用会逐渐明显，当修复概率γ逐渐与传导概率β相同时，即故障节点会被及时修复，故障节点将无法影响正常节点的作业，此时，故障节点的传导能力为0。

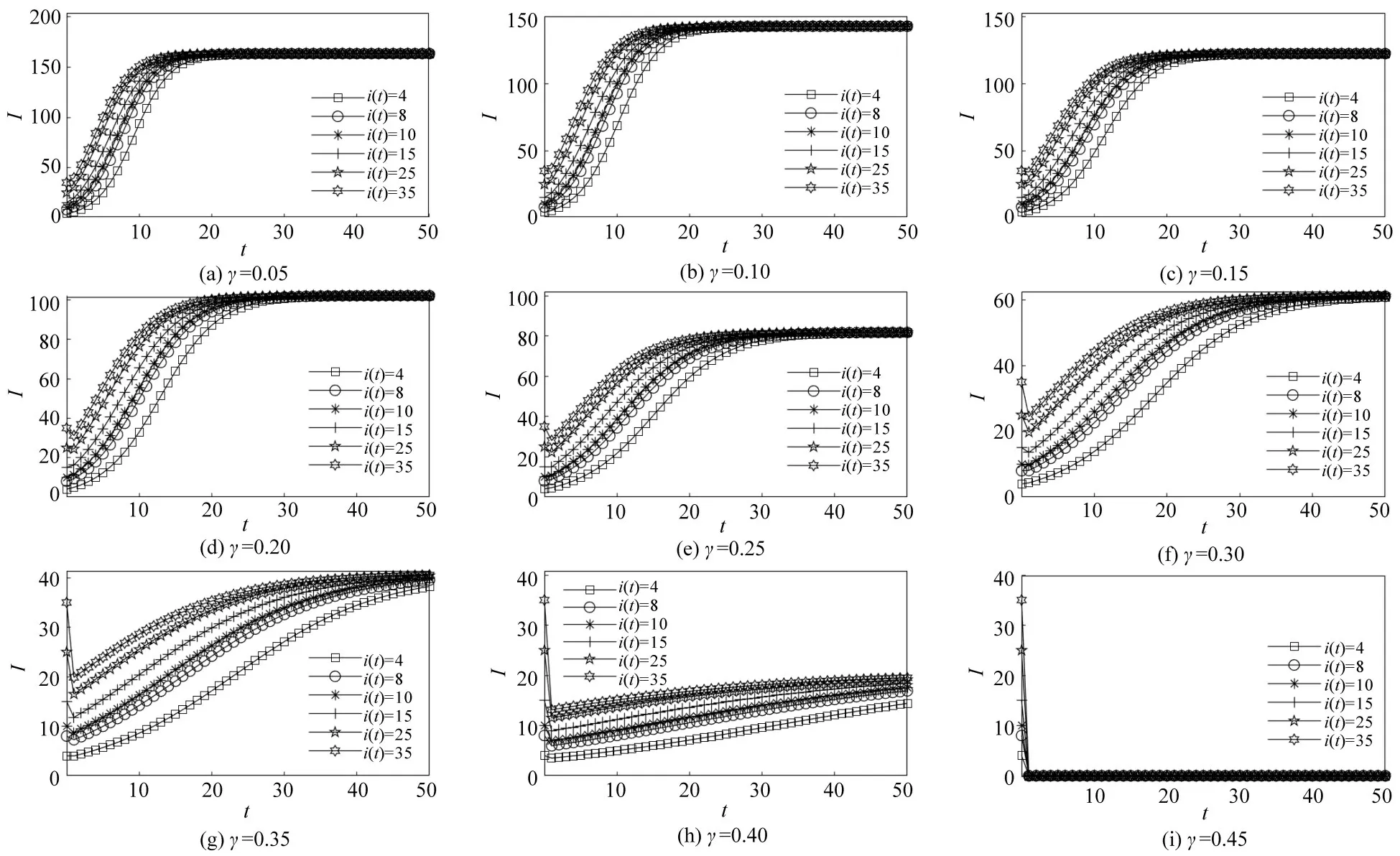
图8 修复概率γ 与传导能力的关系Fig.8 Relationship between repair probability and propagation ability

对于超边数量Ei的增减对传导能力的影响，在本文所构建的自动化码头多级作业超网络中，超边的数量增长意味着码头作业任务的增加，任务越多，网络规模越大。因此，对于超边数量Ei的增减可以考虑为网络总节点数N的变化，因而，根据上文的结论，网络中节点数增加，特征路径长度会增加，传导速度较慢，传导能力降低。

4 结论

本文结合超网络理论和小世界网络理论分析了由不确定事件导致的延误在自动化码头多级作业网络中的传导特性。首先，构建了一个自动化码头多级作业超网络模型。之后，利用特征路径长度和聚类系数等网络拓扑指标分析了所构建网络的结构特性，从传导速度、传导范围及传导能力3 个角度对延误的传导情况进行的数值模拟分析，得出3点结论：

(1)网络的传导速度与网络节点数呈负相关，与故障节点数量成正相关；在网络总节点数N一定的情况下，故障节点数量越多，延误传导的也会越快。另一方面，当网络总节点数N增加时，在实际作业中可以理解为故障节点可替换的选择空间也就越大，即利用网络中其他节点替换故障节点，因而，传导速度会得到一些抑制。

(2)在相同传导概率下，故障节点数量越多，网络的聚集系数越大，网络的传导范围越广，而低聚类特性会抑制延误的传导。

(3)初始故障节点数量越多，传导能力越强，完成SIS 传播过程的时间越短。且在传导概率较小时区分度更高。修复概率则与传导能力呈负相关关系，修复概率越大，传导能力越低。

本文讨论了不确定事件带来的延误影响在自动化码头多级作业中的传导特性，拓展了现有自动化码头多级作业优化的分析方法，揭示了延误的部分规律，并对码头作业网络内部各节点的结构优化、协作等有一定帮助，例如，通过增加节点数量，能够增强码头对于延误的应对能力等。