基于通勤模式的都市圈中心结构判别研究

刘晓冰，李奉孝，田欣妹，闫学东*

(1.北京交通大学，综合交通运输大数据行业重点实验室，北京 100044；2.中国城市规划设计研究院，北京 100044)

0 引言

随着城市化进程的加快，城市规模日益扩大，单中心城市人口集聚带来的负外部效应使城市交通问题日益严重。都市圈空间结构中的城市形态、城市规模、土地利用等都会影响到交通线网布局和交通设施供给，继而影响到交通方式的选择、交通源的空间分布和交通需求总量，最终影响整个都市圈交通系统[1]。因此各地解决城市交通拥堵、提高交通品质问题的思路逐渐从单一扩大供给向供需双侧调节转变，也越来越重视从城市空间规划层面引导交通出行模式的转型，通过城市空间规划和交通组织耦合发展的视角来改善交通问题。

中心结构识别是城市空间规划的重要步骤之一。然而，目前对中心结构的识别在分析方法与数据应用等方面仍然受限。一方面，由于多中心结构的复杂性，目前缺乏成熟的多中心判别理论和衡量方法。目前主要采用如下几种思路：第一，比较某区域之内城市的重要性以及等级分布情况[2]，对城市的首位度进行排名，但是此种比较方式的准确性较低；第二，立足于城市之间的交通网络数据进行识别，如Liu 等[3]针对中国多个主要城市的多中心结构以及此类城市的流量数据进行检测，虽然结果具有较好的代表性和准确性，但此方法立足于高质量统计数据基础之上，耗费的人力和物力相当巨大，更新频率也相对较低，而且没有设置统一的标准[4]；第三，比较城市多中心和理想模型之间的差异，例如Shlomo 等[5]依据对美国城市的调查分析，建立了包括生活-工作社区邻里模型在内的5种假设空间结构模型，但是理想模型的建立尚未达成共识，如果研究区域的内部差异较大，则很有可能出现结果不一致的情况，另一方面，根据传统调查数据对城市结构进行的判别大部分是静态的[6]，获取成本较高且可用性较差，另外受限于数据获取的难度，过去的研究一般都是将行政区作为城市中心结构的基本空间单元，无法对区域发展进行精细化研究[7]，而且行政区规模的差异还会导致不确定的区域偏差[8]。除分析方法与数据应用受限外，现有研究多从一个城市的中心结构展开分析，缺少大规模的实证研究，很难找到普遍规律及普适性的结论。

为了更加科学地制定不同都市圈中心结构下的资源配置和通勤效率优化策略，本文利用百度通勤大数据，聚类识别了都市圈中心布局，提出不同都市圈中心结构下的通勤模式和量化指标，对我国35个重点都市圈的中心结构进行判别，并分析我国主要中心结构下都市圈通勤效率的关键影响因素，为城市管理者开展精细化的空间布局和交通规划提供一定的参考。

1 研究范围与数据介绍

1.1 研究范围

本文研究对象包含全国35个主要城市形成的都市圈区域，是中国超大、特大和大城市的典型代表。具体包括超大城市中的北京市、上海市、广州市、深圳市，特大城市中的成都市、天津市、郑州市、西安市、杭州市、武汉市、青岛市、南京市、沈阳市，I型大城市中的长沙市、济南市、哈尔滨市、合肥市、昆明市、长春市、大连市、太原市、厦门市、乌鲁木齐市，II 型大城市中的宁波市、石家庄市、南宁市、福州市、贵阳市、南昌市、兰州市、呼和浩特市、银川市、海口市、西宁市，以及I型小城市拉萨市，具体分布如图1所示。

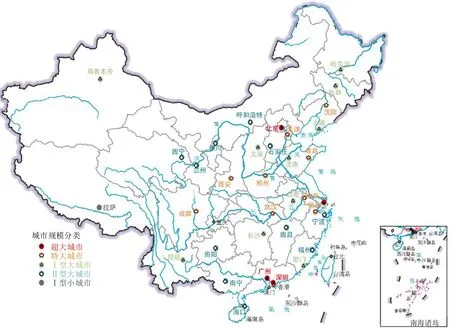
图1 研究城市分布图Fig.1 Study city maps

1.2 数据介绍

本文数据集来源于百度地图位置数据处理后得到的通勤数据，时间范围为2019年1月～6月，共180 余天。出于对个人隐私保护要求，该数据集以0.5 km×0.5 km 栅格为基本单位，每一条数据包含居住地栅格id、居住地栅格中心经纬度、居住地栅格所处行政区划、工作地栅格id、工作地栅格中心经纬度、工作地栅格所处行政区划、通勤人数、通勤时间均值、通勤距离均值等信息，具体字段如表1所示。针对每个待研究城市，统计居民出行O或者D至少一端位于城市行政区范围内的通勤点对，从而建立每个都市圈的通勤数据库。

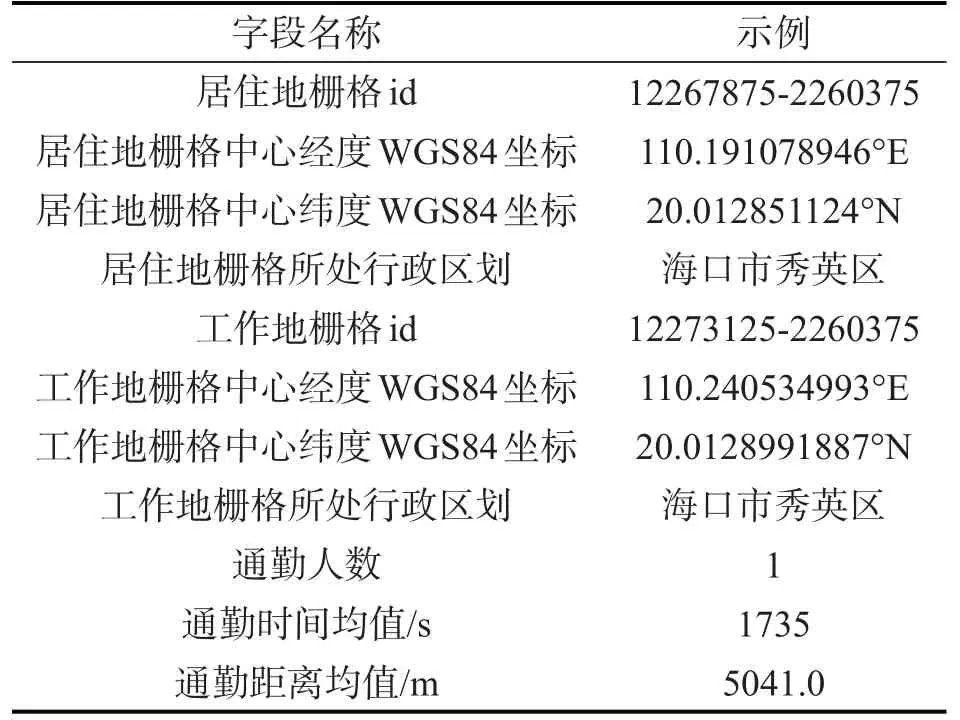
表1 通勤数据字段列表Table 1 List of commuting data fields

1.3 通勤分布分析

利用通勤数据对城市居住就业人口分布进行热力图表征，直观发现人口高密度分布区域和城市中心区域有比较强的相关性。以深圳和天津为例，如图2和图3所示。深圳市除南山区、罗湖区人口密集区域以外，还可以识别出龙岗区、龙华区、宝安区。在天津市，通过人口分布情况可以明显地识别出中心城区与滨海新区两个中心，两中心间相隔较长距离，且中心城区面积大于滨海新区所识别的面积。由此可知，根据通勤人口分布特点对城市中心结构进行初步识别具有可行性。

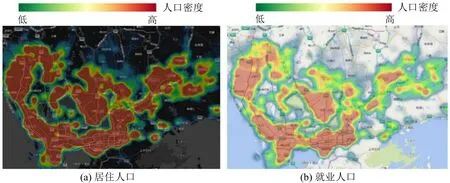
图2 深圳市居住与就业人口分布热力图Fig.2 Thermal map of residential and employed population in Shenzhen

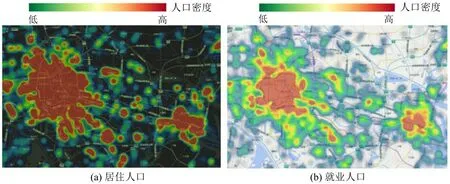
图3 天津市居住与就业人口分布热力图Fig.3 Thermal map of residential and employed population in Tianjin

2 基于聚类算法的都市圈中心布局识别方法

2.1 中心能级测度指标选取

国外对于中心结构的研究中，经常利用就业工作岗位总数量与密度去衡量多中心形态分布[9]，我国对于中心体系的研究一般都是把街道作为空间基本单元，以人口普查数据为基础，再借助密度识别的手段去划分[10]，基于此，本文采用以密度为基础的中心测度指标。对于空间基本分析单元，考虑到以街道为代表的行政区域存在面积不一、范围过大等问题，在中心识别研究中采用空间网格作为空间基本单元，网格内居住与就业人口密度作为网格中心能级测度指标Si，并将城市内所有网格能级指标Si进行以极小化方法做标准化处理，得到修正后的网格能级指标S′i。

2.2 基于聚类算法的都市圈中心识别方法

DBSCAN 算法不受聚类空间形态限制，不用预设聚类个数，能够对噪声进行高效识别，是进行地理空间划分比较常用的方法[11]。对于大规模的通勤数据，传统的算法可能因为数据量巨大导致计算崩溃，为了提高计算效率，本文基于网格进行聚类，将0.5 km×0.5 km 的原始栅格聚合为1.5 km×1.5 km 的空间网格，利用DBSCAN 方法对网格内中心测度能级进行聚类，以实现对都市圈形态中心布局的识别。

基于网格的DBSCAN聚类算法需要重新定义算法中的Minpts、Eps 两参数含义。其中，Eps 为网格邻域搜索半径，取值为2，以保证搜索范围在每个方向上都有相邻网格。Minpts 重新定义为Eps搜索范围内形成集群的最小网格中心能级测度指标Si的加和值，此值的选取应根据不同城市的行政区划和空间功能规划情况具体选取，保证最后聚类结果中各部分的分离程度和聚类个数。最终基于网格与中心能级指标的DBSCAN算法流程如下：

(1)选取研究城市，以网格内居住与就业人口密度作为网格中心能级测度指标，计算城市所有网格的中心能级测度指标，并结合当地城市规划与实际发展选取合适的Minpts 取值。

(2)选择城市任意网格，根据邻域半径Eps 与密度阈值Minpts 判定其是否为核心网格(核心网格邻域内中心能级测度指标加和值大于Minpts)，若是核心网格则选取与其密度可达的所有网格形成一个簇，即为一个聚类。

(3)找到城市网格中所有核心网格密度可达的簇从而找到所有的聚类类别。

(4)未被归于任何簇的网格则标记为噪声点。

3 基于通勤模式的都市圈中心结构判别方法

3.1 都市圈通勤模式理论构建

传统上判断都市圈空间结构的方法是考察城市内部要素密度的分布，比如人口密度分布。然而，城市中心结构模型的许多理论基础都是基于与货物、人员和服务的物理移动相关的流动。因此判别城市空间结构不仅要考察城市区域内的人口或就业分布，还要识别城市区域内不同区域间的流动分布。城市中心结构分布模式直接影响了城市的实际通勤模式，不同的空间结构下的城市通勤数据会呈现出不同的特征[5]。结合中国都市圈空间发展特点和本文通勤数据特征，构建了最大无序通勤模式、单中心通勤模式、均衡多中心通勤模式、非均衡多中心通勤模式以及约束扩散通勤模式等5 种通勤模式，并提出5 种假设模型下理想的通勤连接关系。

(1)最大无序通勤模式

最大无序通勤模式是城市中心结构的一个极端，它假定居住地与就业地之间没有任何吸引力或排斥力。当交通成本为零或可以忽略不计时，可以假设一个城市的居住地和就业地均随机分布，居民通勤流动呈现无序状态，没有明显的规律。

最大无序通勤模式下的通勤距离计算方式如下：首先在该城市的原始居住地与就业地经纬度不变情况下，利用洗牌算法分别随机抽取一个居住地与一个就业地，并且自动生成随机通勤对序列，所求得的平均通勤距离即为最大无序模式下的平均通勤距离，其连接示意图如图4(a)所示。方格代表实际居住地，圆圈代表实际就业地，利用箭头把随机选取的居住地和就业地两两重新连接。

(2)单中心通勤模式

单中心通勤模式先验地假定所有就业地都必须集中在中央商务区(CBD)的一个点上，所有的居住地都围绕着那个点排成环形，居民沿径向路线通勤到CBD 上班。在该模式中，主中心或主中心附近的通勤成本为零或可忽略不计，平均通勤成本随城市规模的增加而增加。从职住的角度分析，理论上主中心的就业占比达到100%。

单中心通勤模式通勤距离计算方式如下：首先，假定该城市的居住地经纬度不变，提取出所有就业地的加权形心点作为新中心就业地；其次，将原居住端与新就业地组成假想OD对，其连接示意图如图4(b)所示。

(3)均衡多中心通勤模式

均衡多中心结构没有明显的主中心，通勤流发生在每个中心的四周，各个中心之间也会有一定通勤上的联系，但联系并不紧密。在这些中心区域，就业地通常位于交通枢纽周围，从职住的角度分析，理想条件下每个中心实现了职住平衡。对于假设具有多中心属性的空间结构下的通勤模式，首先需要对城市市域进行空间划分，本文采用Fast Unfolding 算法对城市网格进行社区划分，这种方法可以保证子中心内部联系更加紧密，不同中心间联系比较稀疏[12]。

均衡多中心通勤模式下理想的通勤连接操作如下：①基于Fast Unfolding城市空间划分结果，对于原始居住地与就业地进行通勤单元划分；②计算每个通勤单元的加权形心点作为每个中心的就业地，即多中心就业地；③每个居住地与其所在通勤单元内的中心就业地相连形成新的OD 对。该模式下的通勤连接关系示意图如图4(c)所示。

(4)约束扩散通勤模式

约束扩散模式则是在多中心模式的基础上，将大多数工作分散在“多中心之外”，腹地居民在通勤范围内并没有将通勤距离作为一个选择就业的主要障碍，因此腹地居民的就业一定程度上是无序选择就业和就近选择就业模式混合。本质上，约束扩散模式是一个混合模式，对于腹地的居民通勤出行可以假设为最大无序模式，对于各中心的居民通勤出行基本符合多中心模式。该模式的特征是比均衡多中心的通勤距离更长，但比最大无序模式或单中心通勤模式假设的通勤距离更短。

约束扩散通勤模式下理想的通勤连接操作如下：①基于Fast Unfolding城市空间社区划分结果，对于原始居住地与就业地进行通勤单元划分；②计算每个通勤单元的加权形心点作为每个中心的就业地，即多中心就业地；③利用洗牌算法随机选取每个通勤单元内3部分的居住地，一部分与其所在通勤单元内的中心就业地相连，第2部分的居住地在不受通勤单元的影响下随机选择其就业地，最后一部分在不受通勤单元的影响下就近选择其就业地，由此形成新OD对。该模式下的通勤连接关系如图4(d)所示。

(5)非均衡多中心通勤模式

非均衡多中心通勤模式对应的中心结构由一个主中心和多个外围分散的次中心组成，大量的通勤交通发生在主中心与次中心之间。相比于单中心通勤模式，主中心的就业聚集向心力减弱；相比于均衡多中心通勤模式，次中心与主中心之间、次中心与次中心之间的就业吸引力存在明显的差距。由于实际操作中很难界定非均衡多中心模型的非均衡度，无法对该模式下的通勤连接关系进行精准的再分配，这里以示意图的方式简单展示其通勤流动关系，如图4(e)所示。

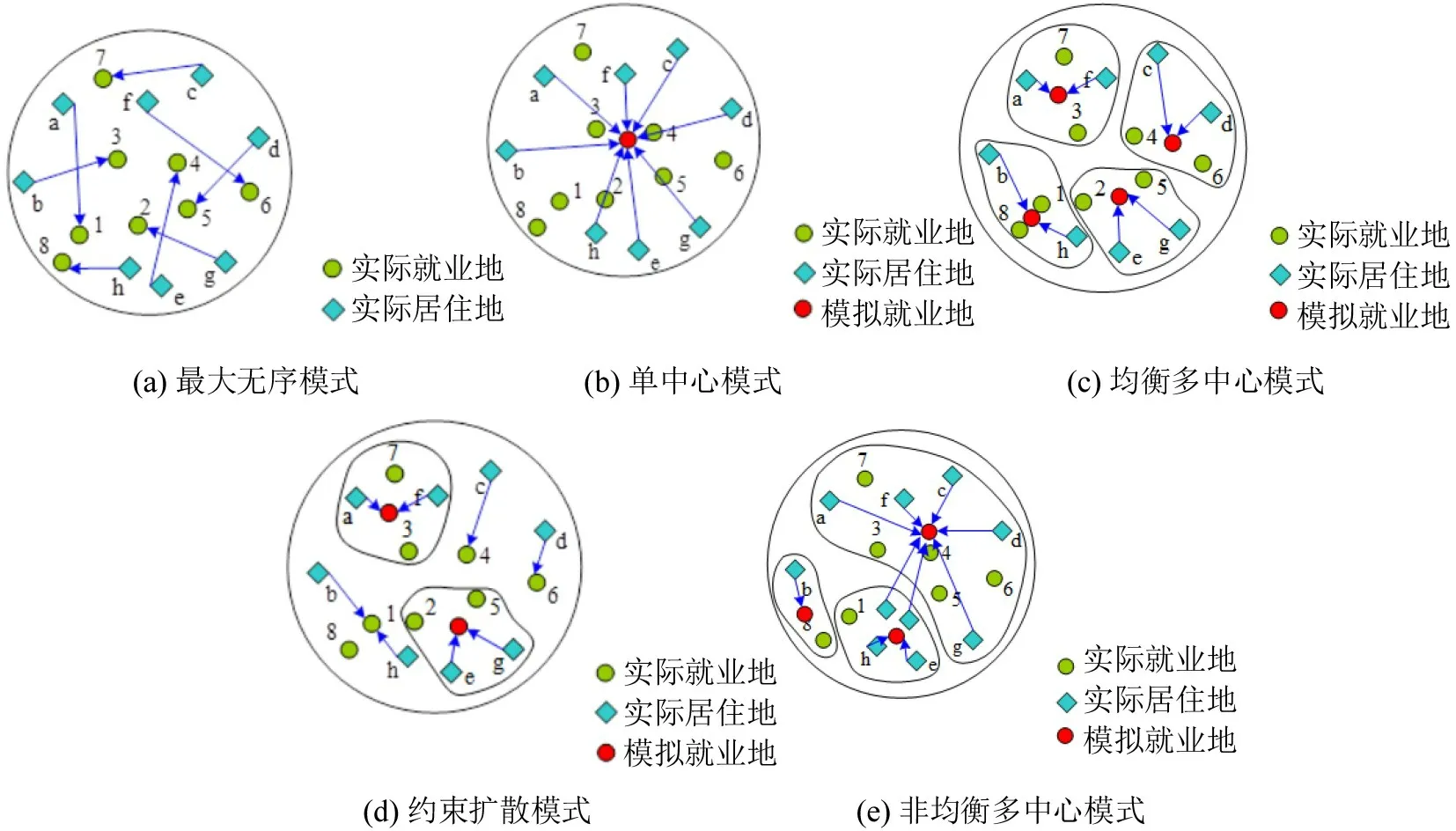
图4 5种假设通勤模式下的通勤流动示意图Fig.4 Schematic diagram of commuting flow under five hypothetical commuting patterns

3.2 都市圈中心结构判别方法

(1)通勤距离与模式符合度

通过通勤距离指标初步判别各研究都市圈的通勤模式。由于非均衡度的不确定性无法精确计算该模式下的理想通勤距离，另外约束扩散模型与非均衡多中心模式对于都市圈平均通勤距离这一指标差异性不显著，需要通过其他方法进行判别。对于通勤距离这一指标而言，计算每个研究都市圈在其他通勤模式下模拟通勤平均距离以及实际通勤距离，然后进行比较。因为受各城市面积及人口密度的影响，不能单纯从实际平均距离与预设模式下的距离最接近而判断为此种模式，因此提出通勤模式符合度Θ概念，横向的对所有城市进行各模式的符合度比较，衡量平均通勤距离更接近此模式的城市。

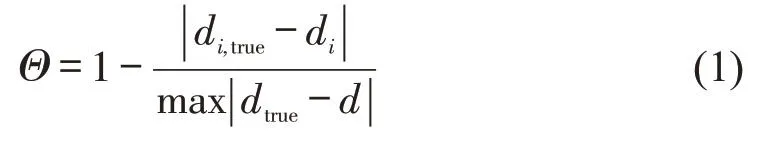
式中：Θ为各模式的实际通勤距离与假设模型进行做差并进行标准化处理；dtrue为各模式实际通勤距离；d为假设模式下的通勤距离；i分别为所研究的35 个城市，i=1,2,…,35；di,true表示城市i的实际通勤距离；di为城市i假设模式下的通勤距离。

(2)区域就业占比

为进一步判别各都市圈的通勤模式，将都市圈中心布局识别研究中识别出的中心作为中心区域，将其他网格作为腹地，计算各中心内网格的平均通勤就业端发生密度，将值最大的中心定义为主中心，其余为次中心，计算都市圈各区域的就业数量占比Ej为

式中：Ej为都市圈中区域i的就业数量占比；Dj为区域j内的就业总数量；j为都市圈主中心，都市圈次中心与都市圈腹地区域，j=1,2,3。

(3)区域职住平衡

除了研究都市圈各区域的就业占比以外，同时也可以从各中心的独立程度来进一步判断每个都市圈各主次中心是否实现内部职住平衡，以此来判断每个中心的发展成熟度，进而判断都市圈中心结构。定义各中心独立指数Im为

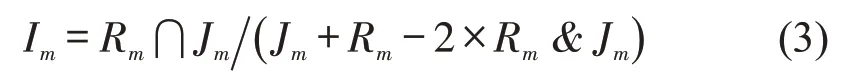
式中：Im为中心m的独立指数；Jm为在中心m内工作的总就业者人数；Rm为在中心i内居住的居民总人数；Rm∩Jm为不仅在中心m内就业，同时又在中心m内居住的总人数；m=1,2,…,n，n为在都市圈中心布局识别研究中识别出的中心数量。

4 结果及分析

4.1 都市圈中心布局识别结果

利用基于网格的DBSCAN聚类算法识别35个都市圈的中心布局，结果发现，该方法识别出的都市圈中心城区轮廓范围清晰，其分布也与各城市规划中的主次中心相吻合，最终结果主要可以分为以下几大类：

(1)识别出强大主中心，主中心的外围区域很难识别出分离度及尺度较为合适的次中心。典型的城市有拉萨市，如图5(a)所示。

(2)识别出多个中心，而且各中心分布较为均衡，没有面积格外突出的中心簇。典型的城市有深圳市，如图5(b)所示。

(3)识别出多个中心，但有明显的主中心，而且主中心外围紧密分布多个次中心。典型的城市有北京市，如图5(c)所示。

(4)识别出多个中心，有明显的主中心，而且主中心与次中心之间有较大范围腹地。典型的城市有天津市，如图5(d)所示。

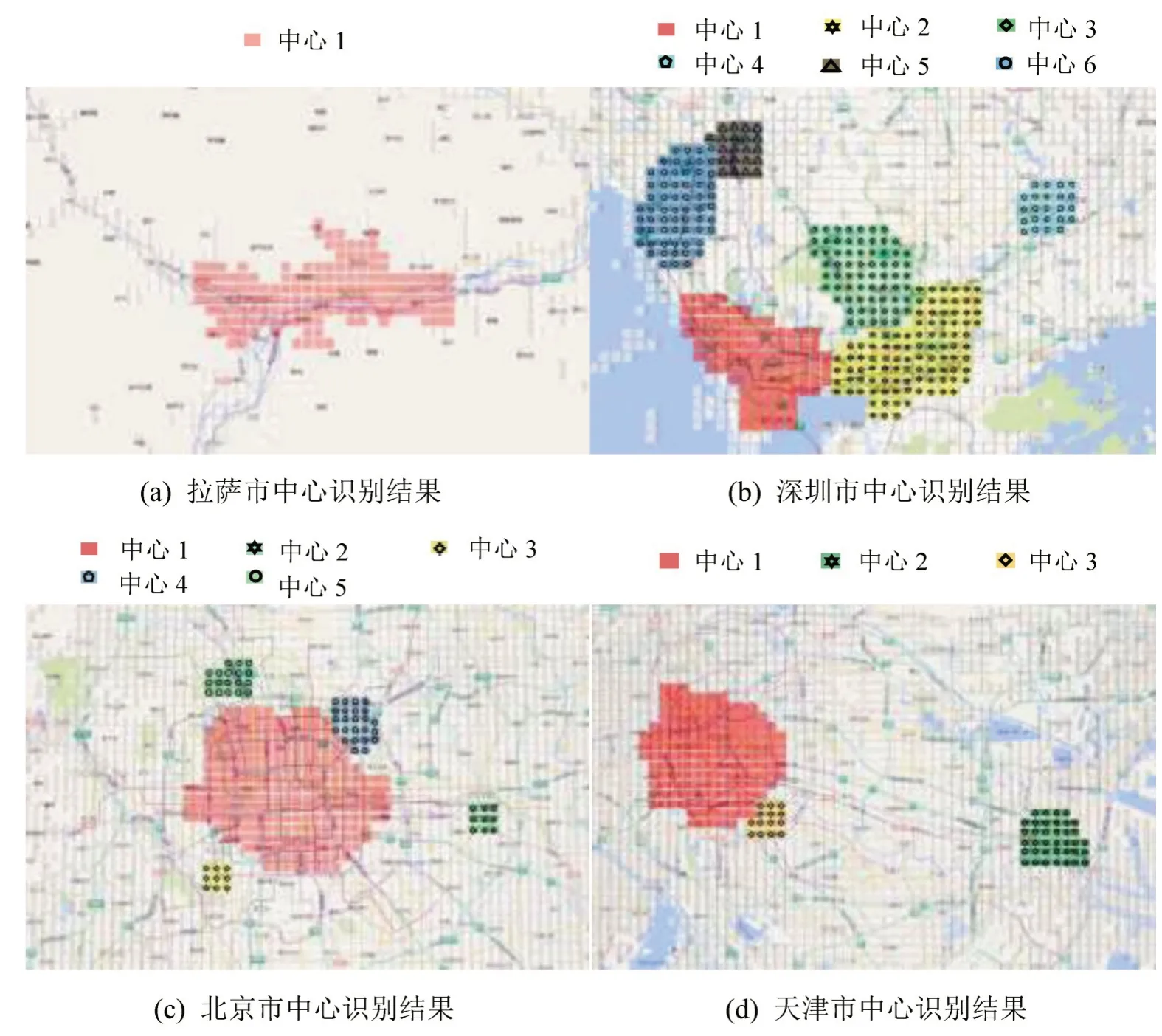
图5 部分都市圈中心布局识别结果Fig.5 Center layout identification results for part of metropolitan areas

4.2 都市圈中心结构判别结果

计算研究都市圈在各假设通勤模式下的平均通勤距离以及实际平均通勤距离，结果如图6所示。所有都市圈的平均实际通勤距离为(7.8±2.3)km。最大无序模式与单中心模式下的平均通勤距离均高于实际平均距离，大多数都市圈实际通勤距离与均衡多中心模式下和约束扩散模式下的通勤距离更为接近。考虑到该非均衡多中心通勤模式属于单中心到均衡多中心的过渡阶段，可以推测这种情况下的通勤距离位于两者数值之间，大多数都市圈实际通勤距离可能与其更为符合。

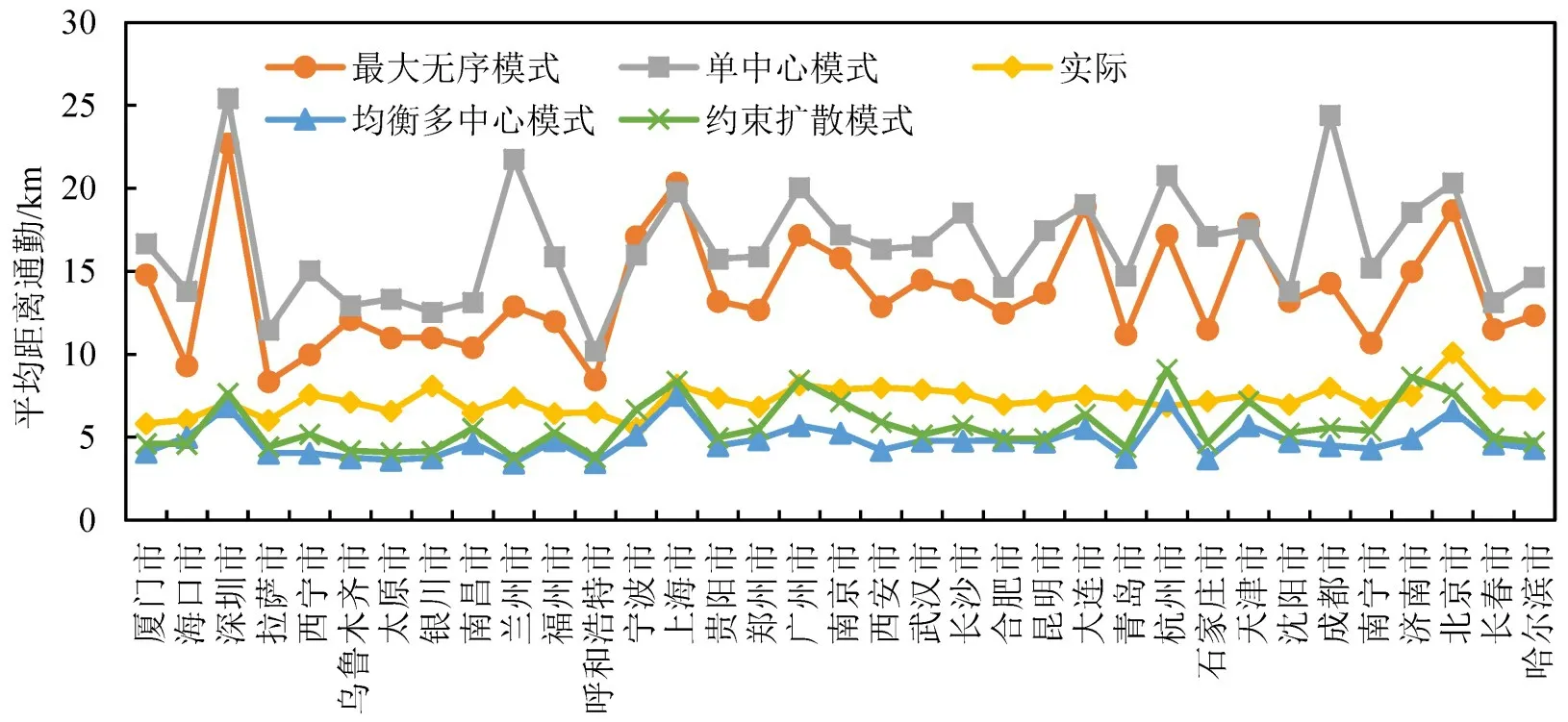
图6 假设模式与实际都市圈平均通勤距离Fig.6 Average commuting distance of hypothesis commuting patterns and actual values

进一步计算都市圈与最大无序通勤模式、单中心通勤模式、均衡多中心通勤模式的符合度，结果如图7所示。可以看到：拉萨市、西宁市、银川市及呼和浩特市都具有较大的无序模式符合度和单中心通勤模式符合度；东北部城市长春市、沈阳市、哈尔滨市以及呼和浩特市也偏向于单中心通勤模式趋势。这类城市就业主要集中在主中心，没有形成一个主中心与多个外围次中心共同均衡发展的就业形势。而单中心通勤模式符合度较低的则为深圳市、广州市、杭州市，说明外围的次中心对主中心也有一定的分散作用。均衡多中心通勤模式下模式符合度最高的城市为深圳市，该城市在图7(a)、(b)两种其他模式下都表现出较低的符合度，基于此对深圳市的判定更倾向于多中心通勤模式，这种判断在其他指标评价中也将进行附征。此外，一些城市在上述分析时可能在每个模式下都没有展示很强的符合度，典型的如北京市，结合其在图5中实际通勤距离介于单中心通勤模式与均衡多中心通勤模式之间，因此将其归为非均衡多中心通勤模式的备选，然后结合其他指标进一步判别。

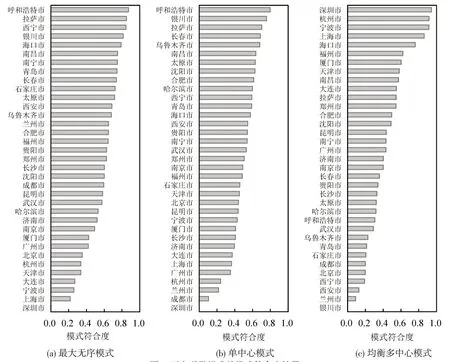
图7 面向通勤模式的模式符合度结果Fig.7 Results of pattern compliance for commuting patterns

对于就业占比这一指标，理想情况下单中心模式下主中心就业占比应更接近于100%；均衡多中心模式各中心占比较为均衡，没有明显的主次中心之分；约束扩散模式下各中心就业占有一定比例，且腹地也有大部分就业占比；非均衡多中心通勤模式各中心占比不等，主中心会有一定主导性。计算各都市圈区域就业占比情况，结果如图8所示。

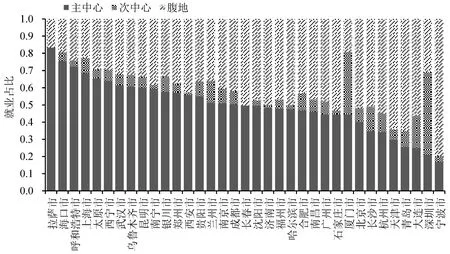
图8 都市圈各区域就业占比Fig.8 Proportion of urban employment

从图8中可以看出，拉萨市、海口市、呼和浩特市、上海市、太原市、西宁市、武汉市、乌鲁木齐市都体现出了很强的主中心性，主中心就业占比超过了60%，但上海市、武汉市除主中心就业占很大比例，还存在多个次中心且也分担了一定量的就业占比；宁波市、青岛市、大连市、天津市则都有较强的就业扩散性，腹地就业占比超过55%，这类都市圈受城市地形的影响，主中心与城市次中心距离较远，导致中心间的腹地成为工作的主要来源。厦门市、深圳市各中心所占的就业总和占比达到了70%以上，腹地就业占比较少。表现出明显的多中心性，识别出的各中心没有明显的主次中心之分，各中心就业占比较为均衡，与基于通勤距离识别出的中心结果一致。

进一步分析各都市圈中心就业占比模式，如图9所示，X轴为在主中心的工作占比，数值由大到小代表单中心度到多中心度；Y轴为所有中心的就业占比，数值大小表示就业集中度。可以看出，多中心集中就业特征最明显的是左上角，深圳市中心体系工作占比很高，但是没有很强的主中心，就业分布在主中心和各个次中心。单中心集中就业特征较突出的是右上角，拉萨市拥有独特的区位和产业结构，展现出很高的就业集中度。而位于左下角的宁波都市圈，主要就业来源不再来自中心体系，而是随机分散在都市圈腹地中，就业去中心化特征明显。

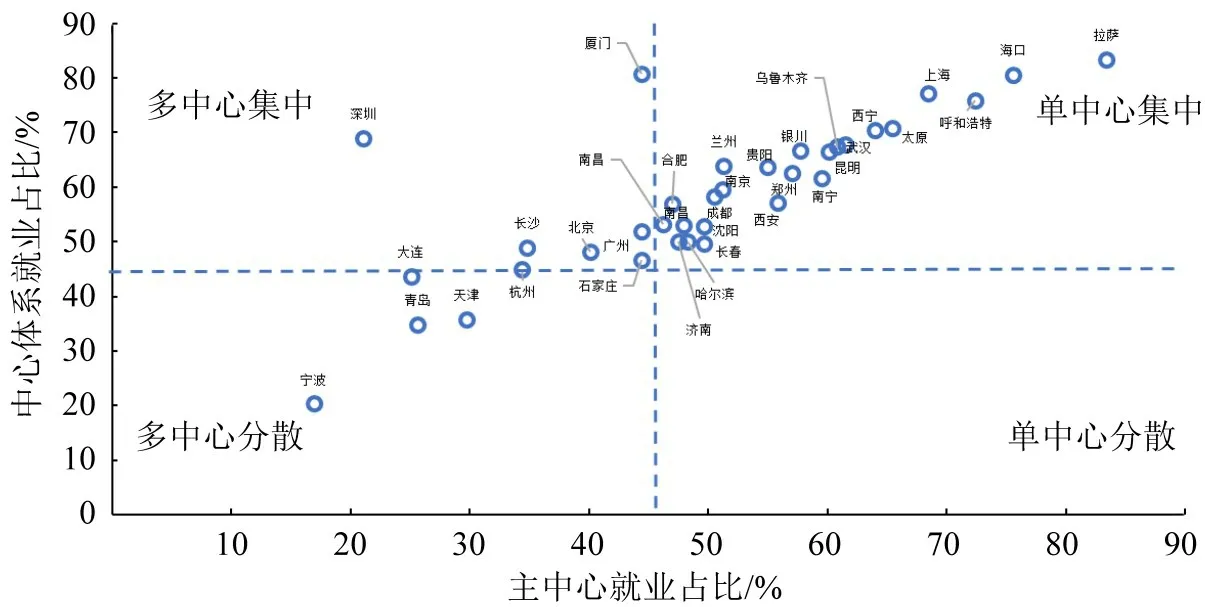
图9 都市圈中心度和就业集中度分布Fig.9 Metropolitan centrality degree and employment concentration index distribution

计算都市圈各区域独立程度，结果如表2所示。数值越大则中心的独立性越强，即本地有较完善的产业支撑本地居民就业，无需通过长距离通勤到其他中心。相反，数值越小则独立性较弱，本地居民需要到周围的腹地或其他的次中心完成通勤。从独立指数中不难发现，全国主要都市圈的次中心独立性都较弱，而展现出较为强大的主中心性，多数都市圈需要到主中心实现就业。拉萨市再一次证明了其强大的单中心性，其在主中心内部实现了很强的就业和工作独立。上海市、郑州市各次中心也展现了较强的独立性，而深圳市、厦门市各中心都较为独立且均衡，是典型的均衡多中心结构。

表2 都市圈各中心独立指数Table 2 Independence index each metropolitan center

最终判别结果发现，大部分都市圈呈现出非均衡多中心结构，主要表现为主中心就业吸引力较强，次中心发展尚不成熟，次中心的独立性较低；其次以拉萨市为代表的多个西北部城市呈现出单中心结构，主中心就业占比达到了60%以上。均衡多中心结构以深圳市为代表，各个中心的就业占比均衡；约束扩散结构的城市多分布在沿海地区，主要特点为主中心就业占比优势不明显，腹地就业占比超过了55%。管理者应该根据都市圈中心结构特征，制定更加具有针对性的资源配置和交通优化方案，例如，对于均衡多中心都市圈，重点是中心内部公共交通及其配套设施的提升，而对于非均衡多中心都市圈，除了各中心内部的完善，还要采取措施满足各中心之间的通勤联系。

4.3 非均衡多中心结构通勤效率影响因素分析

考虑到目前我国大部分都市圈呈现出非均衡多中心的空间结构，从社会经济、空间结构以及交通设施三个维度的影响因素[13]，建立非均衡多中心结构都市圈的通勤效率回归模型。在强制进入方法中，人数、GDP、职住平衡通过0.05水平上的显著性检验，而其他自变量都被淘汰出回归方程。Pearson 相关分析显示，通勤时耗和人口规模(0.636)、职住平衡(-0.243)、与GDP(0.235)在0.01 水平上高度相关。这表明，人口规模增大，人均GDP升高，职住不平衡等原因都会导致通勤时耗增大，具体如表3所示。

表3 非均衡多中心结构多元回归分析结果Table 3 Result of multiple regression analysis of unbalanced polycentric structure

由容许度值及方差膨胀因子可知该模型不存在严重多重共线性，通过了异方差等回归假设的检验，如表4所示。最终回归方程的解释度达到了77.9%，拟合度较好，如表4所示。

表4 非均衡多中心结构多元回归分析解释度Table 4 Explanation degree of multiple regression analysis of unbalanced polycentric structure

在非均衡多中心通勤模型下，人口规模对通勤时耗影响是最大的，其次是GDP。对于经济因素，GDP 比人均收入更能体现对整个都市圈通勤时耗的影响。而职住平衡也是影响非均衡多种心的一个重要因素，因此越接近均衡时，都市圈表现出越高的通勤效率。非均衡多中心结构下通勤时耗回归方程为

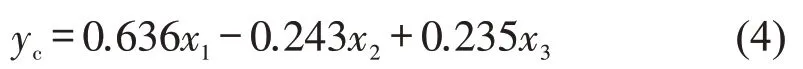
式中：yc为非均衡多中心结构下的通勤时耗；x1为城市人口(万人)，x2为职住平衡指；x3为城市人均GDP(万元)。

控制都市圈发展规模，推进各中心居民当地就业，提升职住平衡关系，从而能够提升通勤效率。

5 结论

本文以都市圈通勤大数据为驱动，采用基于网格的密度聚类算法识别都市圈中心布局，并提出5种通勤模式的理论模型，基于通勤距离、就业占比、职住关系等指标判别各都市圈的中心结构，最后针对普遍存在的非均衡多中心结构的通勤效率影响因素进行回归分析，得出以下结论：

(1)不同都市圈的中心布局差异明显，基于网格的密度聚类方法能够体现小空间单元之间的空间相互作用，比基于行政区划单元的结果更加精细有效、客观合理。

(2)大多数都市圈实际通勤距离与均衡多中心模式下和约束扩散模式下的通勤距离更为接近，远低于最大无序模式与单中心模式下的平均通勤距离。

(3)大部分都市圈表现为非均衡多中心结构，其次为单中心结构，而少部分表现为约束扩散结构和均衡多中心结构，不存在符合最大无序结构特征的都市圈。不同中心结构的分布呈现出一定的地域特征，单中心结构都市圈主要位于中西部城市，而约束扩散结构和均衡多中心结构都市圈大多是由东部沿海开放城市发展形成。

(4)城市规模与通勤时耗的相关性最为显著，路网密度与通勤时耗相关性不显著。社会经济因素中的GDP比人均收入更能反映对整个都市圈通勤时耗的影响，职住平衡度对通勤时耗也有较大影响，非均衡多中心结构都市圈应提高职住平衡度来提升通勤效率。

上述研究结果对中国主要城市中心空间结构特征进行了深入地剖析，为针对性地制定不同都市圈的资源配置策略和通勤效率优化策略提供了有效支撑，对都市圈空间规划和交通可持续发展具有一定的理论价值和现实指导意义。