高峰期考虑乘客议价的网约车定价与平台收益及社会福利优化

王健，王慧，胡晓伟*，李园园

(哈尔滨工业大学，a.交通科学与工程学院；b.经济与管理学院，哈尔滨 150090)

0 引言

《网约车市场及发展趋势分析》报告显示，2015年，中国网约车年需求次数为635.1百万次，在政策推动下，2016年下半年网络预约出租车用户规模增长了41.7%[1]，2018年用户通过滴滴平台完成的行程总里程累计为488 亿km，行程总时长达到17 亿h，2019年滴滴出行累计运送乘客超过1.9 亿次。网约车的快速发展使得网约车定价越来越受重视。网约车定价策略影响政府、网约车平台、司机和乘客等多方的利益。《网络预约出租汽车经营服务管理暂行办法》规定按照高品质服务、差异化经营的原则，有序发展网约车，同时网约车运价实行市场调节价。网约车市场受到天气、乘客和司机实时数量等因素的影响，采用固定出行价格不能体现市场的时变性，同时，随着乘客自主性的增加，其在选择是否乘坐网约车时也渴望更多的权力，所以，研究制定一个满足平台和政府方利益的动态价格并考虑赋予乘客一定的自主议价权力对市场的影响具有重要的理论意义和实用价值。

关于网约车动态定价问题，国内外许多学者都进行了研究。Zha等[2]研究了不同劳动力供给假设下的均衡模型，发现与静态定价相比，使用激增定价或许能增加平台和司机的收入。Cachon 等[3]利用产生分析和数值结果的程式化模型，研究了包括激增定价在内的多种定价方案，最终发现所有利益相关者都可以在使用具有自调度能力激增定价的平台中受益。Tian 等[4]在双向市场理论的框架下，进行了基于运输服务的供需分析，建立了运输服务市场的中介定价模型，并根据纽约市的出行记录数据进行了模拟，结果显示，网约平台在早高峰时段定制更高的价格，能吸引更多的驾驶员并缓解乘客的需求压力。孙中苗等[5]针对网约车平台在需求波动市场中存在乘车需求竞争以及乘运供应竞争的定价优化问题，以平台利润最大化为目标，运用最优控制论方法，构建了基于不同竞争情形的网约车平台动态定价模型，并求得最优动态竞争价格解以及乘运供应率与需求率的变化轨迹。Chen 等[6]提出了一种动态空置车辆与乘客交会模型，研究短期变化和当前需求与供给对市场的干扰。赵道致等[7]使用乘客出行需要等待的时间描述影响出行需求的服务质量，分析了乘客出行需要等待时间对自身剩余的影响以及调整参数对市场不同共同存在的影响，司杨等[8]研究发现网约车进入市场后社会总成本会下降，但会随着市场需求的增加而大幅增加。

从上述国内外现状可以看出，现阶段对于网约车动态定价的研究主要借助排队论、生灭过程等方法描述司机的运行状态，然后基于社会福利最优和平台利润最优建立模型确定定价，对需求的动态变化特征关注较少。根据市场均衡理论，随着市场中商品价格的升高，将会出现需求量下降，供给量增加的情况。在网约车市场中，存在着能够支付高于正常打车费用的乘客，其相对于普通人而言拥有更高的支付意愿。乘客议价就是允许乘客在高峰期提高自己的出价，通过影响乘客、司机双方的效用，进而影响双方进入市场的数量，改变各个时间段的匹配量，对其进行分析研究或有助于得到更高的社会福利，平衡乘客、司机及平台方的利润。因此，本文从网约车需求的动态变化特征入手，赋予乘客高峰期自主议价权力，制定满足网约平台、司机、乘客以及社会利益的动态定价模型。

1 基于动态匹配的网约车定价模型

1.1 动态匹配模型

为了精确描述网约车市场运行状况，本文采用动态匹配模型[9]作为基本理论。动态匹配模型能够反映出短期变化对网约车市场的影响，适用于短期内变量的研究。从图1可以看出，动态匹配模型通过将整个工作日划分为若干个小的区间，在每个区间内都进行订单的匹配，最后在一天结束时进行市场出清，不影响下一个工作日的市场运行。

考虑将1 d 分为长度均为24×60J的J个时间段，在每个时间段内，乘客与网约车之间的匹配数量根据一定的定价策略确定，表示为匹配量函数[6]，即

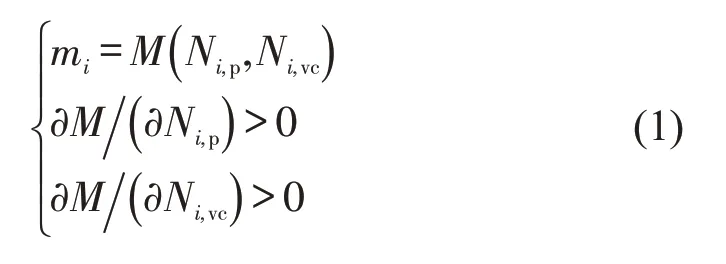
式中：mi为匹配量，表示第i时间段内乘客与空置网约车的匹配数量；M(Ni,p,Ni,vc)为匹配函数；Ni,p为第i时间段内有出行需求的乘客数量；Ni,vc为第i时间段内处于空闲状态的网约车数量。

假定该匹配量函数满足Cobb-Douglas 型生产函数，则式(1)可写为

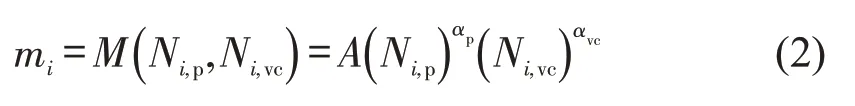
式中：A为匹配参数，与网约车服务区域及市场特征相关；αp、αvc分别为匹配量对未匹配乘客数、空置网约车数的弹性。

记k为起始时间段至i时间段之间的时间段值，Ak,p、Ak,vc分别表示第k时间段乘客、网约车的到达量，它们受到价格和佣金率的影响；Lk,p、Lk,vc分别表示第k时间段乘客、网约车因某些不确定因素导致离开市场的离开量，则有

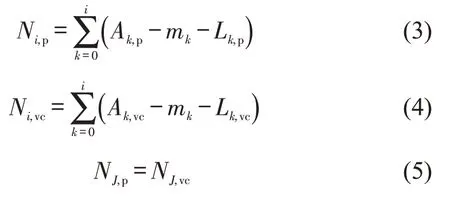
将式(3)和式(4)代入式(2)，匹配函数改写为

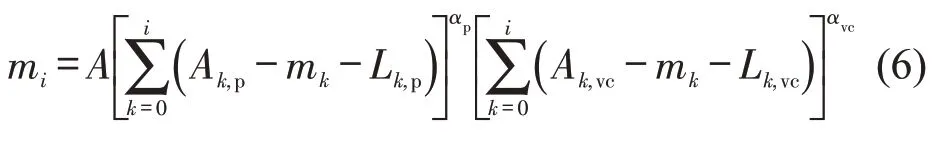
1.2 供求函数模型

在网约车市场中，供给方和需求方是影响市场变化的根本要素，因此，为了确定供给和需求函数，首先需确定乘客剩余和司机剩余。

将i时间段单个乘客剩余[10-11]描述为

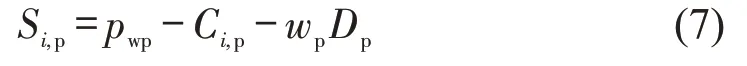
式中：pwp为乘客出行一次愿意支付最大价格的均值；Ci,p为乘客在订单中实际支付的平均费用；wp为乘客向平台发出出行需求后直到乘坐网约车的平均等待时间；Dp为乘客单位等待时间的负效用。

在模型假定的网约车市场中，i时间段乘客的平均等待时间可以用该时段有出行需求的乘客数量Ni,p及匹配数量mi之商来描述，但由于匹配量mi是未知的，采取上一时间段匹配量mi-1、有出行需求的乘客数量Ni-1,p预估i时间段的匹配量，有，故平均等待时间为

i时间段价格变化因子βi影响该时段的乘客出行费用，不同的βi下，乘客将支付不同的价格，pu为乘客出行单位时间需支付的费用，使用βi与pu之积表示乘客单位等待时间的负效用，即

对于司机而言，从平台接单到接到乘客所耗费的时间，以及行驶过程中的油耗、时间等成本都是影响其是否出行的因素，可将i时间段单个司机剩余描述为

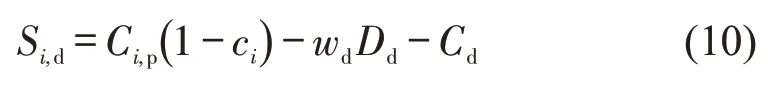
式中：ci为平台的佣金率；wd为司机接到乘客的平均行驶时间；Cd为司机的油耗、时间等成本；Dd为司机从接单地点抵达乘客位置过程中单位行驶时间的负效用，考虑到网约车司机无法路边载客，所以认为接乘客时的负效用很小。

在动态匹配网约车市场中，各时段乘客的到达量受到乘客负效用的影响，随着负效用的增加，选择网约出行的乘客数量会降低，所以其对相邻时间段乘客到达量Ai+1,p有着修正作用，受文献[6]的启发，构建需求函数为

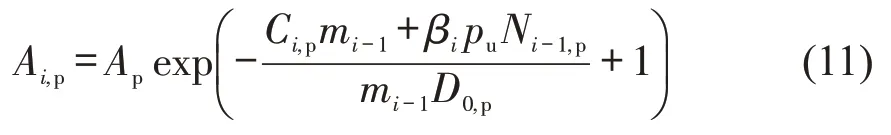
式中：Ap为乘客基准到达量，由当地人口数、经济水平确定；D0,p为初始时段乘客负效用。

与需求函数不同的是，司机的供给受到初始时间段司机效用的正修正，对于司机来说，当进入市场获得的收益变高，会增加下一时段进入市场的供给者数量Ai,vc，故构建供给函数为

式中：Avc为司机基准到达量，由当地人口数、经济水平确定，S0,d为初始时间段司机效用。

1.3 平台利润模型建立及最优化

对于第i时间段，得到平台收入为佣金率、订单数量和费用的乘积，即

式中：ci为平台对网约车司机的佣金率；pi为i时间段内所有订单的平均费用。

考虑全天可得

综上，平台利润为

式中：Oc为平台运营成本；Wd为平台支付的工资，本文将Oc与Wd之和描述为平台收入的某一比例。

由于每个研究时间段内基准单价并不相同，故i时间段内所有订单的平均费用为

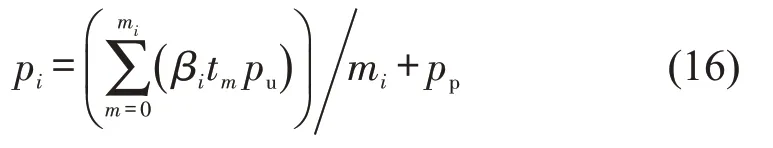
式中：pp为网约车起步费；tm为时间段第m个订单的运行时间；pu为单位时间出行费用。

综上，平台利润最优化问题可表示为

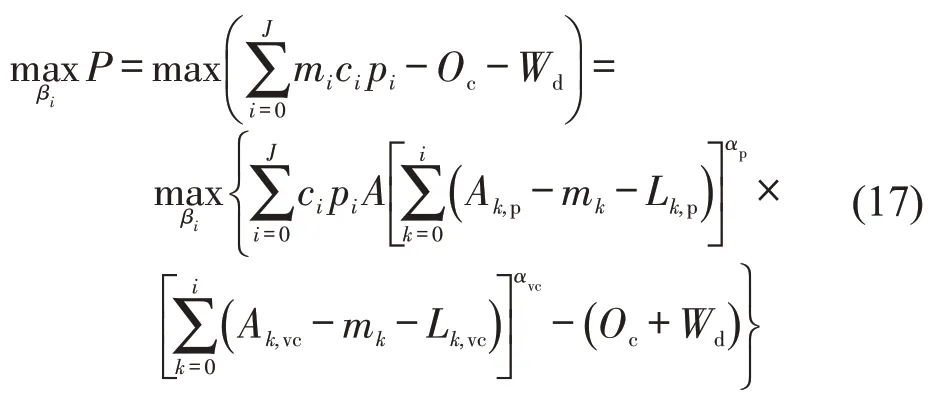
1.4 社会福利模型建立及最优化

社会福利是可以从经济交易中获得的社会总利益[6]，在网约车市场中可表示为乘客剩余、司机剩余及平台利润之和。

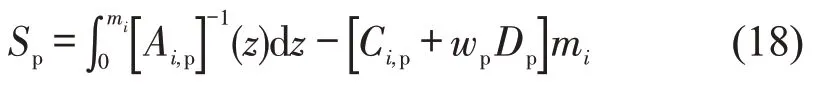
式中：z为网约车市场中的需求。

对于司机而言，其能从网约车市场中获取的利益为司机从订单中获得的收入Ci,p(1-ci)mi与其愿意接受的最小收入之间的差额，故司机剩余描述为

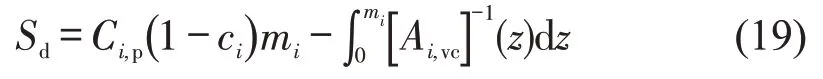
当用Pi描述i时间段平台收入时，网约车市场中的社会福利可描述为

由此社会福利最优化问题描述为

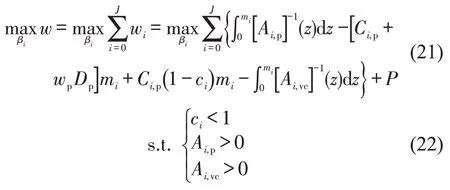
2 基于乘客议价的网约车定价模型

2.1 乘客议价机制

从文献[12]可知，网约车市场中，存在着能够支付高于正常打车费用的乘客，其相对于普通人而言拥有更高的支付意愿。因此，在所研究的网约车市场高峰时期，当允许乘客议价时，急需出行的乘客可以提高自己的出价，进而提高网约车市场乘车费用。根据市场均衡理论，随着市场中商品价格的升高，市场需求量下降，供给量增加，在网约车市场中表现为部分乘客由于高昂费用而退出市场，同时吸引空置网约车进入市场，推动网约车市场向供求平衡移动。

本文采取半个研究时段订单匹配量与基准匹配量(平峰时段订单匹配量均值)的比率来模拟乘客议价的影响，即用f(φ)表征乘客议价在网约车市场中的影响。研究的网约车市场由高峰时段(上午及下午)和平峰时段共同构成。乘客议价机制的作用表现为：平峰时段不进行修正，在高峰时段，当乘客主动提高自己的出价后，部分低出行需求乘客将退出市场，同时吸引其他区域或暂未进如市场的空置网约车加入。

2.2 考虑乘客议价的定价模型

乘客议价会直接影响市场中供给方与需求方的数量，对于乘客来说，当提高自己的出价时，自身负效用会增加，相同的，当减少出价时，负效用又会下降，因此，将式(11)中的需求函数改写为

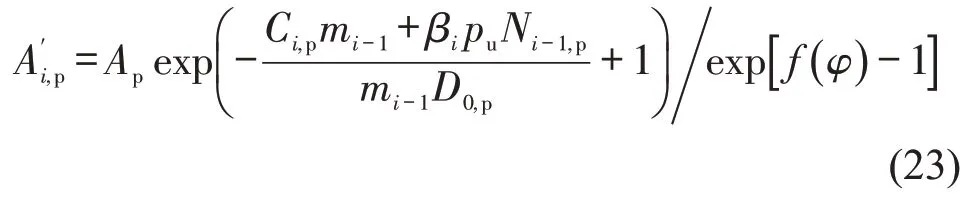
对于司机来说，随着乘客出价的提高与降低，自身效用也在增加和减少，网约车市场对空置网约车的吸引力也会发生同样的变化，故式(12)可改写为

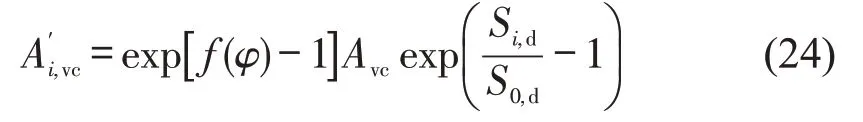
将乘客议价加入高峰时段平均价格更新平均定价公式为

将式(23)和式(24)代入式(6)，得到考虑乘客议价情况下的匹配量函数为

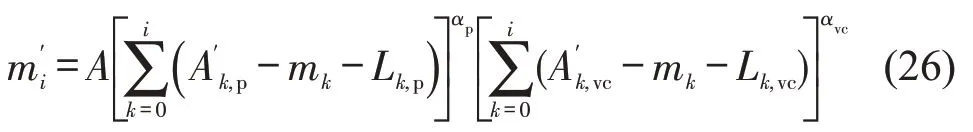
更新平台利润及社会福利模型，则乘客议价下平台利润最优化模型为

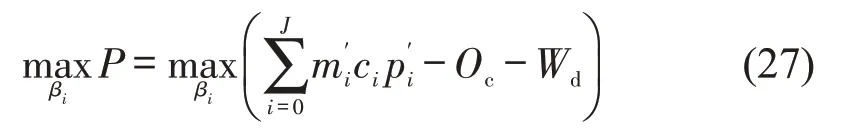
乘客议价下社会福利最大优化问题为

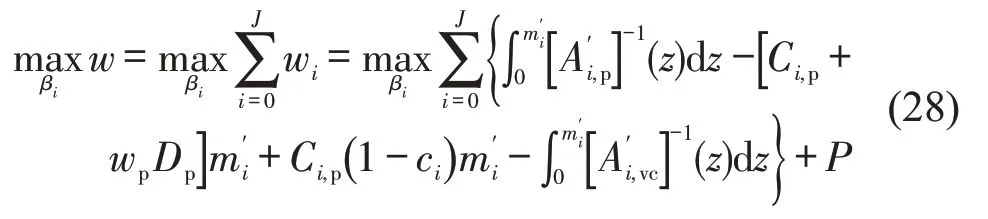
基于图2求解算法可对比分析市场乘客议价对网约车市场的影响。

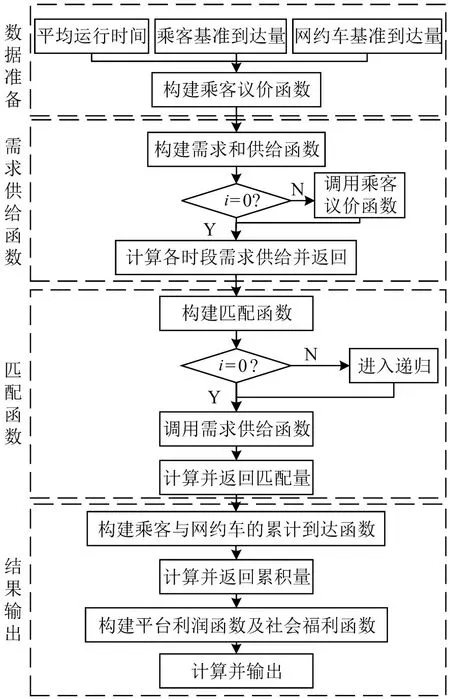
图2 求解算法流程Fig.2 Flow of solution algorithm

3 算例分析

使用数值算例验证本文提出的平台利润最优模型及社会福利最大定价模型的有效性。设某一网约车市场符合以下条件：匹配参数A=10，弹性因子αp和αvc均取值为0.55[13-14]，平台所有成本占平台收入的21%[15]，即Oc+Wd=0.21P，平台佣金率ci=0.25，单位时间出行费用pu=120 元⋅h-1=2 元⋅min-1[6]，网约车起步费pp=10 元，乘客出行一次愿意支付最大价格的均值pwp相对于平均价格pi的倍数服从均值为1.2、方差为3的正态分布N(1.2,3)[10]，司机成本Cd为收入的30%，各时间段匹配订单平均时长、乘客基准到达量、网约车基准到达量均从已知数据中挖掘。

考虑到乘客和网约车司机在制定网约车出行计划后，往往不会轻易改变自己的想法，故在算例分析中视匹配失败后的离开量为到达量的微小扰动，则匹配函数表示为

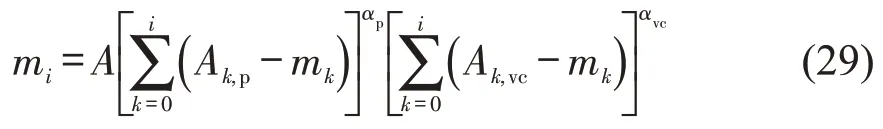
从图3可得，构建匹配模型的订单匹配量与实际市场中订单匹配量基本一致，其R2达到了0.9794，能够比较准确地反映现实市场中各研究时段的订单匹配数量，模型具有可行性。

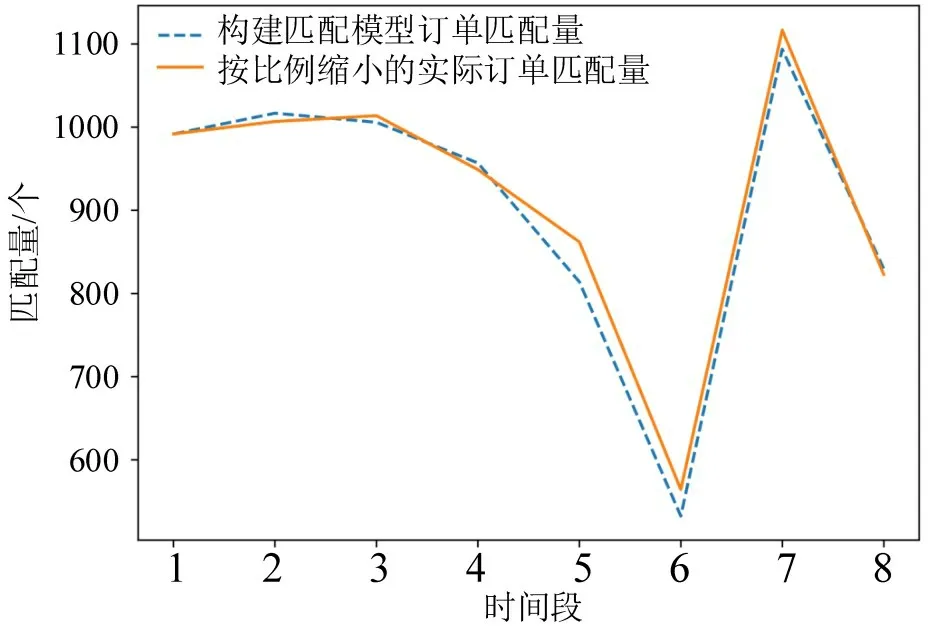
图3 动态匹配模型与实际市场订单匹配量对比Fig.3 Comparison of dynamic matching model and actual market order matching volume

3.1 价格变化因子函数标定

本文采用分段函数来描述价格变化因子在动态匹配网约车市场中的变化。将上海市2016年12月22～24日滴滴出行量取日平均值，并将其定义为一个研究日，将其分成24个研究时段，则价格变化因子为各研究时段(30 min)匹配数量与全天平均匹配数量(总匹配数量/总时间段数J)的比值。

在一个研究日中，价格变化因子将随着订单匹配量的变化而变化，特别是对于高峰时期和低谷时期，价格变化因子将表现出截然不同的变化状态，将其描述为一个函数并不能准确地描述价格变化因子在一天中的变化。分段函数将随着时间段的不同，获得不同的结果，符合网约车市场中价格变化因子的变化规律，因此，构建价格变化因子的分段函数如图4所示。

图4 价格变化因子分段函数Fig.4 Price change factor piecewise function

由图4分析可知，价格变化因子可描述为

式中：t为时间。

由图4可知：在0：00-9：00之间，价格变化因子R2达到了0.9786，9:00-19:30 之间为0.8192，19:30-24:00 之间为0.9809，因此该分段函数能够较准确地描述价格变化因子的变化状况。

3.2 乘客议价影响因子函数标定

在网约车市场中，高峰时段由不连续的两部分构成，平峰时段乘客并不进行议价，故本文研究的乘客议价影响因子函数包含两部分，具体如图5所示。

由图5可得：8:00-10:00间，乘客议价影响因子函数f(φ)的R2在两个时间段分别达到了0.8285与0.8944，说明该函数能够较准确地描述乘客议价影响因子的变化。

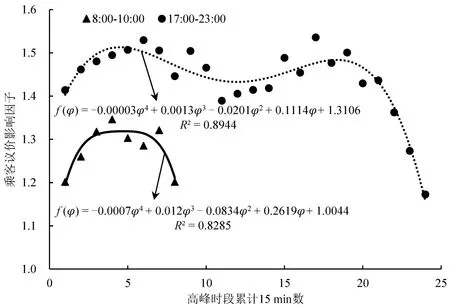
图5 高峰时段f(φ)Fig.5 Peak time f(φ)

因此在所研究的网约车市场中，乘客议价对市场的影响描述为乘客议价影响因子分段函数f(φ)，即

式中：φ为整数，从所在时间段开始，每15 min加1。

3.3 正常网约市场算例分析

保证平台佣金率、进入市场的基准到达量不变，选取下午高峰第3时段分析研究价格变化因子对社会福利的影响，如图6所示。

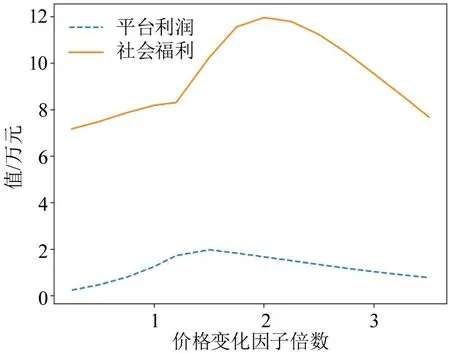
图6 不同价格变化因子下平台利润及社会福利Fig.6 Platform profit and social welfare under different price change factors

从图6可以看出，随着价格变化因子倍数的增加，平台利润和社会福利均先增后减，且具有基本一致的趋势。在倍数为1.5 时，平台利润达到了最大值，倍数为2.0时，社会福利达到最大值。

通过求解动态匹配模型，得到匹配订单量如图7所示，可知，匹配数量变化趋势也同社会福利基本一致，但匹配量在价格乘数变化倍数为1.3 时达到了峰值，提前于社会福利。

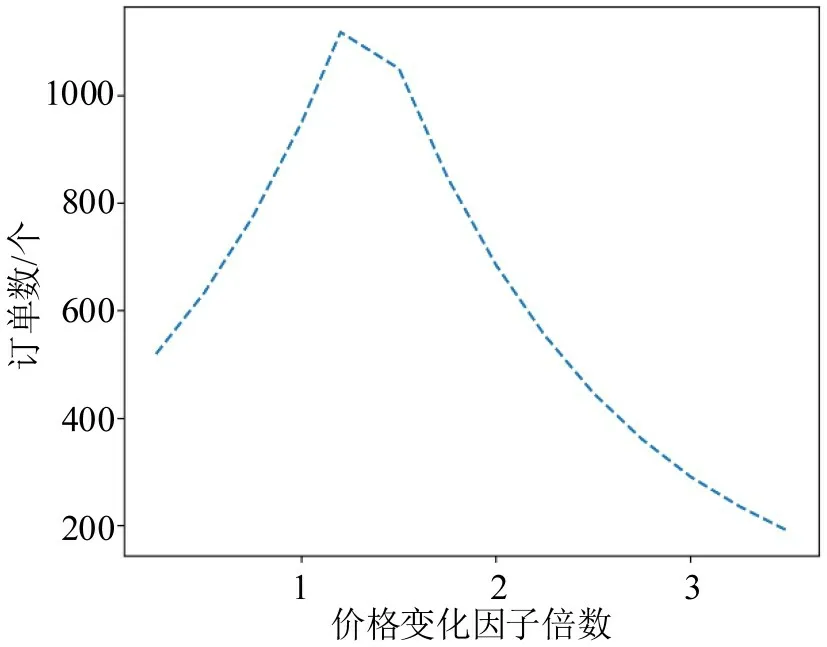
图7 不同价格变化因子下订单匹配数量Fig.7 Order matching quantity under different price change factors

3.4 乘客议价市场及正常网约车市场对比分析

当网约车市场中引入乘客议价后，相比于无乘客议价的市场，乘客议价市场中各时段平台利润、社会福利、订单匹配量及平均价格都将发生变化。

对正常网约车市场和乘客议价影响下的市场中下午高峰时段价格求解可得表1，可知相比于正常状态，乘客议价帮助市场获得更高的社会福利和平台利润，但匹配订单的平均价格也有明显的提高，说明乘客议价增加了乘客出行的负担。

表1 乘客议价前后各时段订单平均价格Table 1 Average price of orders at each time period before and after passenger bargaining

对正常网约车市场和乘客议价影响下的市场中下午高峰时段平台利润、社会福利及匹配量求解计算可得表2，可知，在正常网约车市场下午高峰时段中，随着时间的增长，市场订单匹配量波动较小。在乘客议价影响下的市场中，下午高峰时段订单匹配量先下降后上升，说明在迫切出行乘客增加出价后，部分乘客将退出市场，随着时间的推移，市场中空置网约车数量相对于乘客数量的比例逐渐上升，市场向供求平衡移动，订单匹配量开始回升。

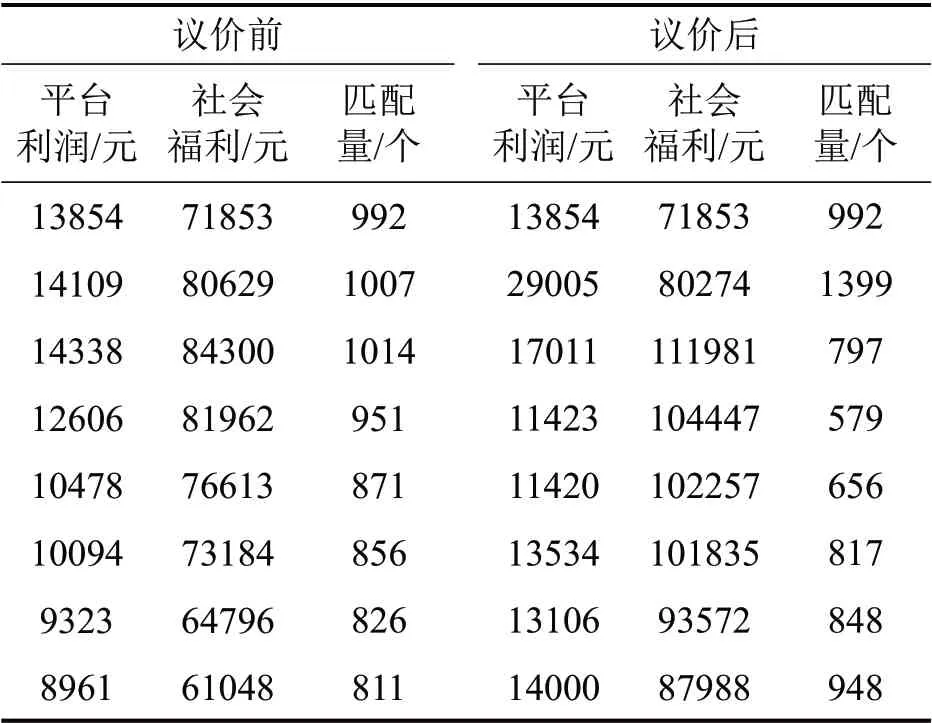
表2 乘客议价前后各时段平台利润、社会福利及匹配量Table 2 Platform profit,social welfare and matching volume at each time period before and after passenger bargaining

将正常状态市场和乘客议价市场下午高峰时段的累计平台利润、累计社会福利、各时段平台利润和社会福利可视化，如图8～图11所示。从图中可知：乘客议价增加了网约车市场高峰时段的累计平台利润和累计社会福利。在实行乘客自主议价后，市场的平台利润及社会福利会出现突然增加的现象，之后有所回落，平台利润甚至出现低于议价前市场平台利润的现象。随着时间的推移，平台利润略微回升并维持在相对稳定的状态，社会福利则在突增后逐渐回落，并维持在相对稳定状态。

图8 下午高峰时段累计平台利润Fig.8 Cumulative platform profit during peak afternoon hours

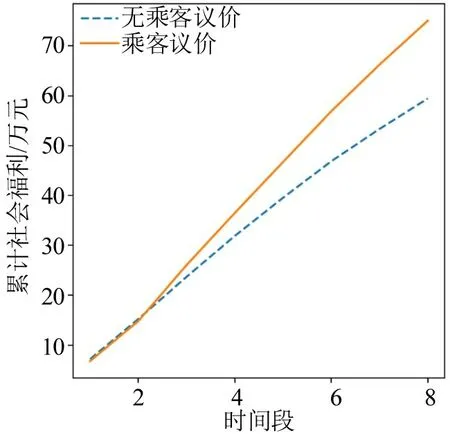
图9 下午高峰时段累计社会福利Fig.9 Cumulative social welfare during peak afternoon hours

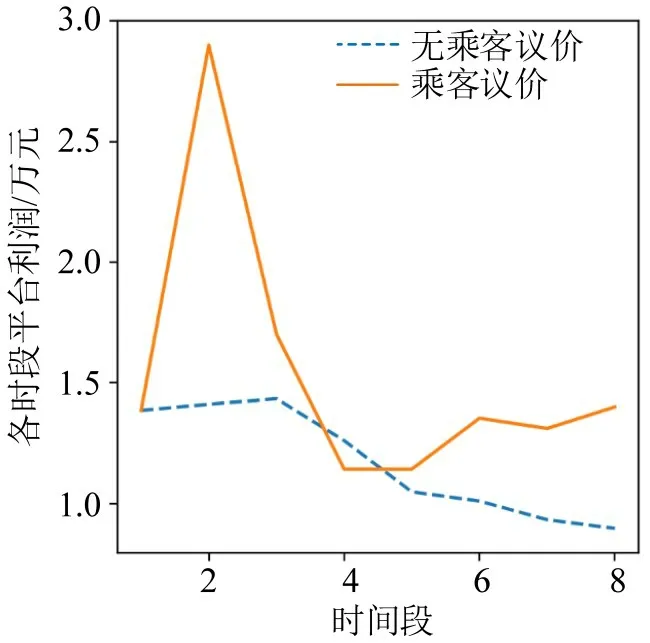
图10 下午高峰各时段平台利润Fig.10 Platform profit during peak hours in the afternoon

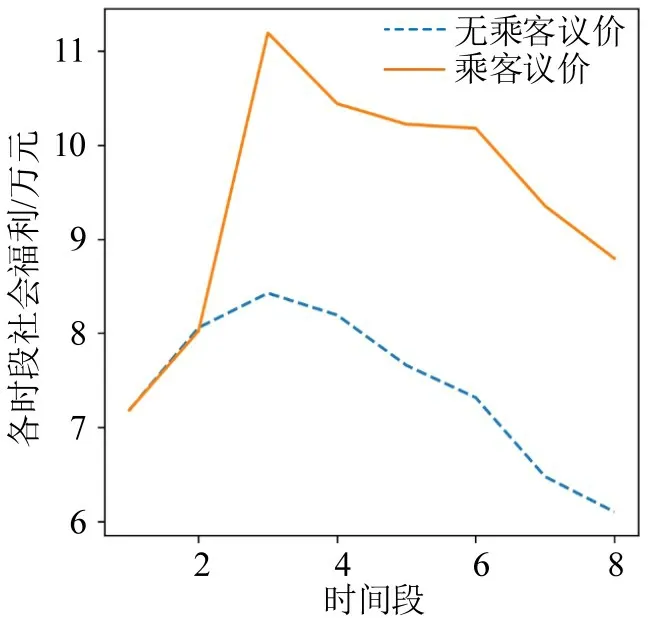
图11 下午高峰各时段社会福利Fig.11 Social welfare during peak hours in the afternoon

4 结论

本文得到主要结论如下：

(1)基于动态匹配构建平台利润及社会福利定价模型并制定求解算法。确定网约车市场供给和需求函数，构建了平台利润模型并将平台利润最优化问题模型化，在平台利润模型的基础上加入乘客剩余和司机剩余的影响构建了社会福利模型，将单位乘客剩余和单位司机剩余模型化，实现了社会福利模型最优化，并制定了求解算法求解定价模型。

(2)提出了乘客议价方法。平峰时段对乘客和司机不进行修正，在高峰时段，当乘客主动提高自己的出价后，部分低需求出行乘客将退出市场，同时吸引其他区域或暂未进入市场的空置网约车，促进市场趋于平衡。

(3)分析了价格变化因子和乘客议价对社会福利的影响。在固定佣金率网约车市场中，随着价格变化因子倍数的增加，社会福利、平台利润和匹配量先增后减，在倍数为2.0 时，社会福利达到最大，倍数为1.3 时匹配量到达最大，当有不同优化目的时，应根据实际目的选择不同的价格变化因子变化倍数。在固定佣金率和价格变化因子市场中，乘客议价能够增加社会福利、平台利润及订单匹配量，但与此同时，乘客议价也提高了匹配订单的平均价格，增加了乘客出行的成本。

本文没有考虑乘客能够接受的最高出价等因素，在后续的研究中可以继续增加此类限制条件；在进行价格乘数变化分析时，可以同时变动平台抽成，分析价格变化因子和平台抽成的共同作用；在定价模型的构建中，可以增加天气、政策等因素的作用，增加定价模型的准确性与实用性。