考虑时间价值的中非多式联运路径与出海港选择

冯芬玲，孙楠佳

(中南大学，交通运输工程学院，长沙 410075)

0 引言

为增加对航运企业吸引力、提升自身竞争力，通过参与内陆运输、发展内陆港等方式，港口积极发展内地腹地及多式联运网络[1]，随着集疏运网络的逐步完善，各地纷纷出台补贴政策，促进综合运输体系建设、区域经济协调和运输方式转变，港口腹地范围已突破传统地理空间的约束，港口(群)与港口(群)之间的交叉腹地在不断扩大，处于内陆地区的托运人如何选择合适的出海港及到港集疏运方式值得关注。

目前，关于出海港及到港集疏运路径、方式选择的研究较少，且多是对海港的各项指标进行专家打分[2]，在选定港口的情况下，选择到港多式联运的路径，两者是相对分离的。在实际的托运行为中，托运人可能并不完全掌握港口各类服务指标的信息，更加关注的是班期和报价等因素。

货物的不同属性也可能造成出海港选择的差异。冯芬玲等[3]基于货物价值特性、数理化理论III对“一带一路”运输货物进行分类。根据数理化理论，利用货物品类样本两点间的欧式距离，选择Ward 系统聚类分析方法对货物分类，当阈值为6时，货物被分为4大类。近些年，越来越多的学者将货物的时间价值考虑到路径选择成本中进行优化分析，刘畅等[4]针对高价值、高时效性的笔记本电脑，建立综合物流成本最低的中欧路线优化模型。

在多式联运路径优化问题中，不确定性问题的探究已经成为热点问题。不确定条件下的路径优化问题多集中于运输时间、中转时间、客户需求、货运量及运输速度等方面[5-6]，而针对运输价格的不确定性研究较少。

本文综合考虑班轮的班期、运输报价及货物的时间价值，综合港口选择和到港运输路径、方式，构建路径选择模型，在此基础上选取两种货类[3]，调整分析不同出海港的海运报价，以期为实际的出海港路径选择和运力资源调配提供参考。

1 问题描述

随着“一带一路”共建的推进，中非加快命运共同体的构建，国际多式联运业务不断拓展，海港在运输过程中扮演着不可替代的角色。一般而言，集装箱运输的内陆成本约占整个“门到门”运输的40%～80%，内陆运输的时间与成本对托运人选择港口具有很大影响[7]，因此，将到港口选择和到港运输路径、方式综合考量十分必要。托运人对于运输路线和方式的选择需要综合考虑不同因素，最直观的体现是考虑时间和费用等，针对不同价值的货物，综合考虑的着重点不同[3]。在出海港选择问题上，托运人往往是基于船公司或其授权的货代的运输报价和航线的发班时间及班次频率来考量，对于港间距离差别不是很大，可能需要等待班轮到港的情况下，货主的选择很大程度上会相应发生改变。

因此，本文提出基于货物时间价值的多式联运路径及出海港选择模型，与一般的多式联运路径规划模型相比，综合考虑班轮的报价、班期及托运人对于不同价值的货物愿意付出的等待成本，综合港口选择和到港运输路径、方式，构建模型。

2 模型建立

2.1 货物时间价值成本

国际多式联运全程运输时间相对较长，会发生货物价值衰减，即货物贬值情况，不同价值属性的货物对时间的敏感程度不同，贬值可用时间价值成本进行量化。本文的货物时间价值成本由资金占用成本及货物价值损失两部分构成。

(1)资金占用成本

货物具有价值，货物在途时间造成企业资金的闲置，限制了货主资金的流转，因此，资金占用成本[4]为

式中：Tα为资金占用成本；λ为银行日利息；Pr为货物初始价值，r为不同的货类；t为运输总时间。

(2)货物价值损失

货物价值会随着供求关系、消费者偏好、市场行情及产品技术含量等发生变化，对于高价值、高敏感度货物而言，更新速度快，市场周期短，很容易被竞争企业抢占市场。远洋运输时间跨距大，所以，在产品运输过程中，产品价值随着时间的推移出现贬值。本文假定货物贬值率为常数，则有，求解微分方程得到其时间价值函数[3]满足：P(t)=Prexp(-ωt)，经t时刻，货物的价值损失为

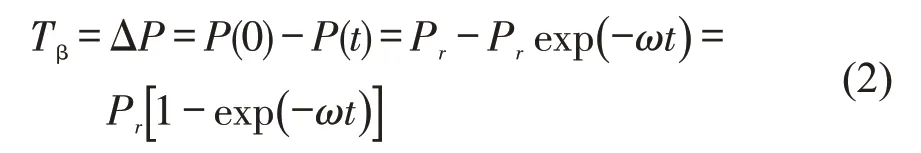
式中：Pr为货物初始价值；ω为货物贬值率(常数)。

综上所述，货物的时间价值成本为：g(P,ω,t)=Tα+Tβ。

2.2 考虑货物时间价值的中非多式联运路径及出海港选择模型构建

2.2.1 模型假设

(1)同一批货物在运输过程中不可分割，即同一批货物在运输过程中只能以整体为单元进行运输，不可被拆分成两个及以上部分分别进行运输。

(2)每个中转节点都具有足够的货物中转能力。

(3)转运只能在运输节点处，且在此节点每批货物至多发生1次运输方式的改变。

(4)公路、铁路及内河运输不受出发时刻的限制，港口班轮运输需按照发班表运行。

(5)航运公司及其货代的报价在一段时间内不变。

(6)不考虑特殊时期及特殊货物报关时间等要求的影响。

(7)不考虑运输过程中天气、运输设备故障及货损等因素的影响。

2.2.2 符号说明

本文模型参数与变量符号定义如表1所示。

表1 模型参数与变量Table 1 Model parameters and variables

2.2.3 目标函数

本文是从托运人的角度对远洋集装箱多式联运路径及出海港进行选择，主要目的是让产品尽快进入市场，减少营运成本，因此，构建运输成本及运输时间最小的双目标模型。

目标函数为

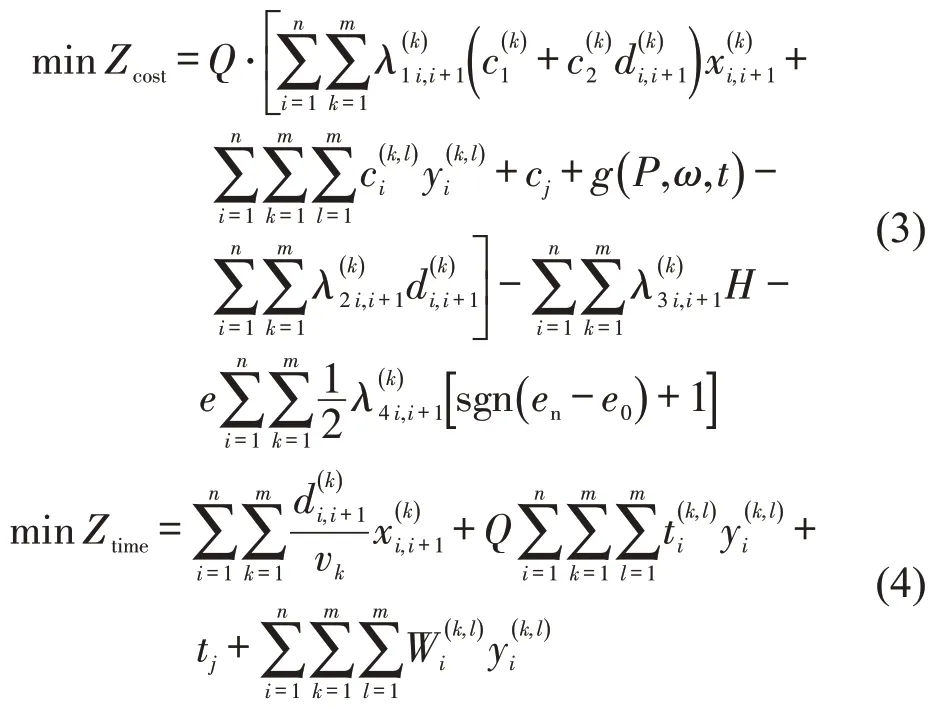
约束条件为

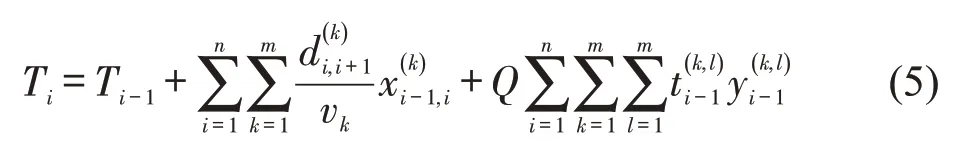
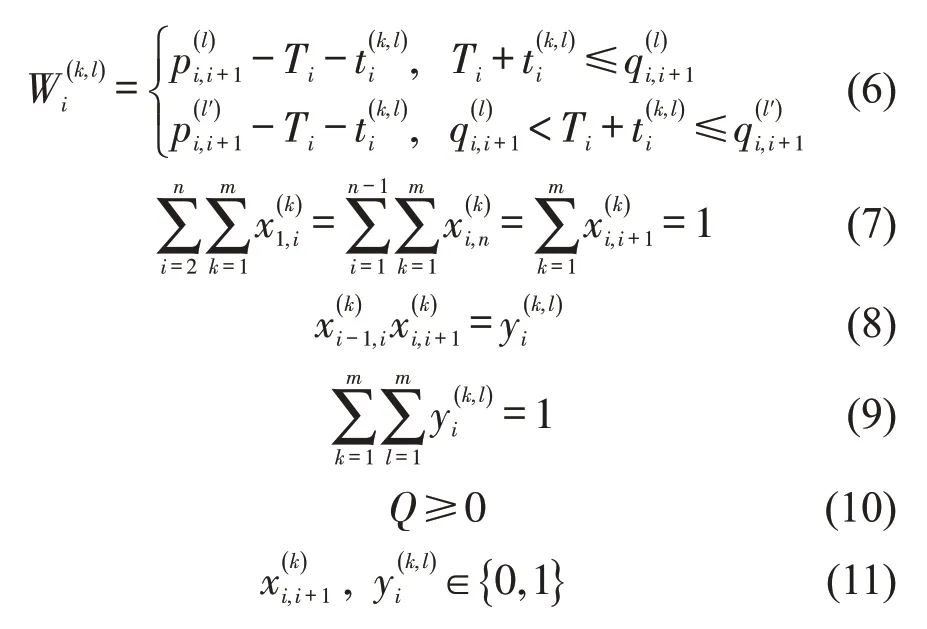
式(3)和式(4)分别为运输成本和运输时间的函数。对于特定运输方式(铁水联运和公水联运等)的补贴也会影响货物至不同港口的运输成本[8]，因此，运输成本函数由货物的在途成本、转运成本、获得补贴的相反数、航运公司运输报价及产生的货物时间成本构成。补贴一般分为货币补贴和税收减免两种形式，其中，货币补贴可细分为固定的货币补贴和浮动的货币补贴[9]。因此，在模型构建中加入补贴项的相反数，λ1代表对符合条件的海铁联运集装箱班列采取的铁路运价下浮优惠系数；λ2、λ3分别代表按运输距离、重量要素计量的和按箱数计量的对于运输的货币补贴系数，H为集装箱数量；λ4代表对年纳税额达到一定标准的企业给予税收优惠系数，该单项式代表分摊到此次运输的优惠金额。式(5)表示货物当前实际到达节点i的时刻。式(6)表示在节点i处货物由于班期时间窗限制产生等待的时间。式(7)保证货物必须从起点出发运送到终点，且保证两节点之间只能选择1种运输方式。式(8)保证运输过程的连续性。式(9)保证同一节点上只能进行1次运输方式的转换。式(10)表示货物运输量不能为负数。式(11)定义了决策变量为0-1变量。

这是多目标优化问题，一个目标的优化往往导致其他目标的背离，因此，可对各个目标赋权值来考虑系统的优化，将其转换为单目标函数运用精确或启发式算法进行求解[9]。

3 实例研究与分析

本文以长沙-德班(南非)为例，假设有1 个20英尺集装箱(配货毛重17.5 t)，需从长沙选择沿海港口出海运往南非德班港，可供选择的出海港口有钦州港、广州港及上海港等10个港口，每相连的城市节点之间有铁路、公路及水路中的若干种运输方式连接。

3.1 算例介绍

该算例的银行日利息λ取值为0.11644‰，当前许多中非联运的项目(例如，湘粤非班列)尚在探索试验阶段，海铁联运的补贴政策尚不统一且在试行，因此，本文具体算例中有关补贴的系数简化取为0 或1。后续考虑班轮班期的实验中，假定A 点各类运输方式的启运时间均为8:30，班轮从港口启航的时间为8:00-23:00 之间，通过python 生成随机数得到班轮的具体离港时间。通过查阅船公司网站、锦程物流网、官方文件以及参考文献[3,10]等方式搜集得到其他所需算例数据，算例的联运网络如图1所示，部分原始数据及经初步处理的数据如表2～表6所示。

图1 长沙至德班多式联运网络Fig.1 Multimodal transport network from Changsha to Durban

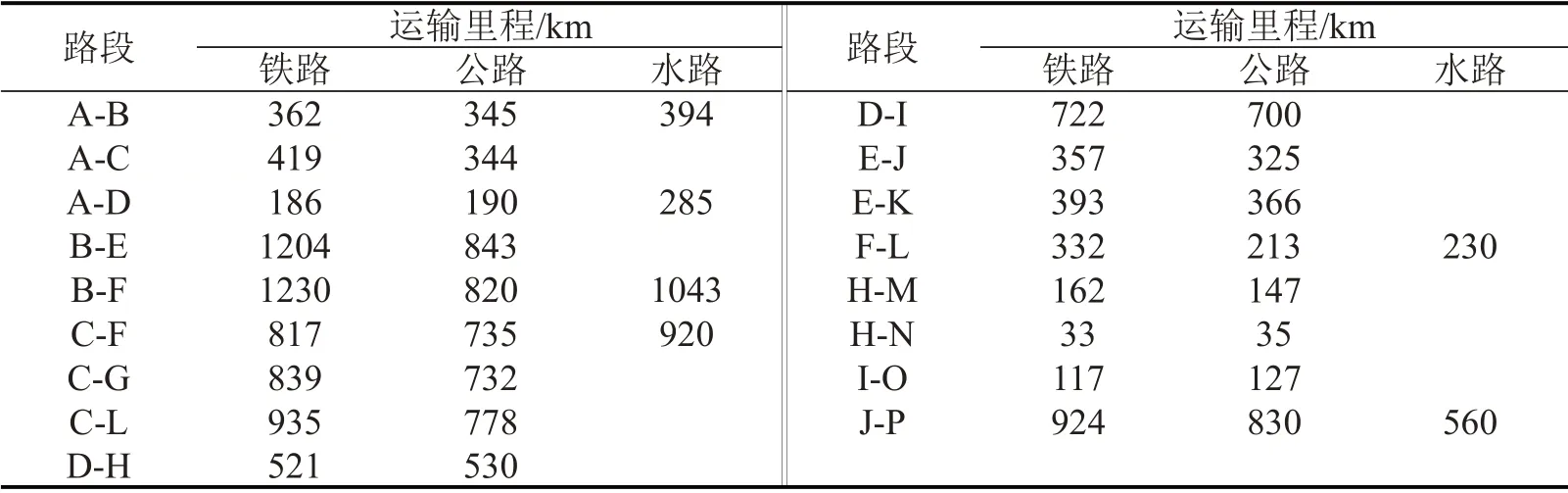
表2 路段运输里程Table 2 Transport distance

表3 各运输方式的运价、运速及中转时间、费用Table 3 Price,speed of each mode of transportation and transit time,cost

表4 各港口航班班次信息及海运价格Table 4 Flight information and shipping price of each port

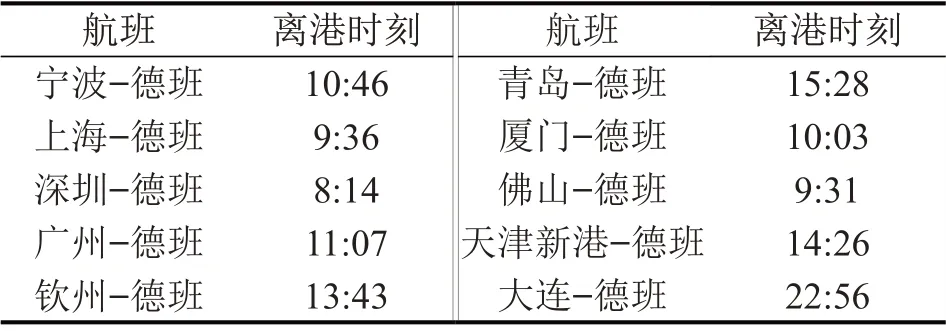
表5 班轮开行时刻Table 5 Liner departure time

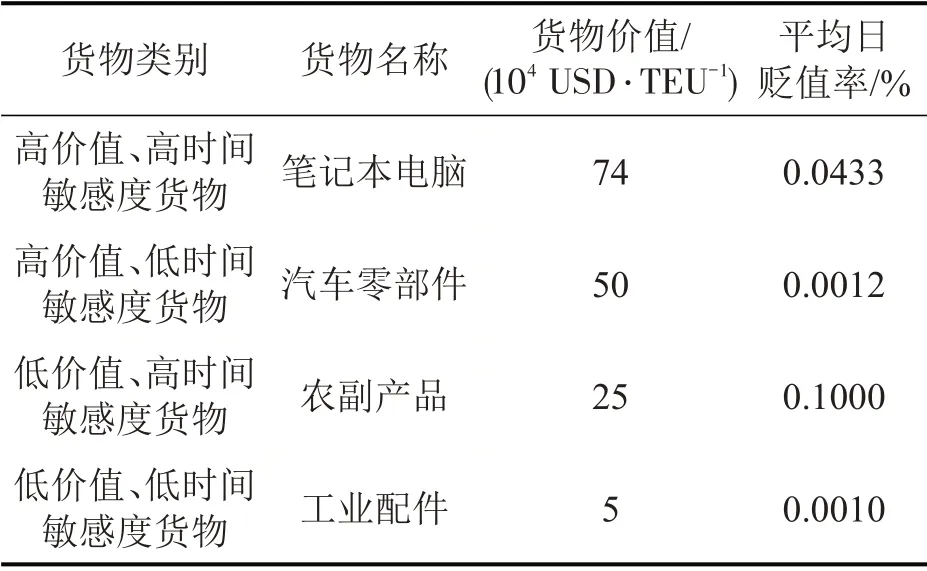
表6 货物基本属性Table 6 Basic attributes of goods

3.2 模型求解及结果分析

效益背反是物流领域普遍存在的现象，成本和时间这两个目标函数之间存在较为明显的背反关系且量纲不统一，需要分别对两个目标函数进行无量纲化处理：，将多目标转化为单目标函数便于求解[10]，定义适应度函数为，其中，托运人对于成本的敏感度等级为(弱;中;强)=(1;3;5)；对于时间的敏感度等级为(弱;中;强)=(1;3;5)。综上，其相对权重系数由于本文分析次优港及到港路线的选择和海运报价对于路径选择行为的影响，因此，对原有网络进行变形[11]，拓展原始节点，例如，图1网络中A-B 节点由公、铁、水3种运输方式组成，分别将其拓展为A-B1、A-B2、A-B3，以此类推，完成所有虚拟节点的增加，采用深度优先遍历的算法进行精确求解。算法过程如下：第n类货物从起点A 出发，先访问A，并将A 标记划分到已访问的集合中，接着访问与A相邻的未被标记的节点i，将其标记划分到集合中，继续从i出发，访问与其相邻并未被访问的节点i+1，重复这一过程直至终点Q，得到其路径数组及适应度值。再次回溯至起点A，选择与A相邻的未被标记的节点进行上述选择计算，直至与起点A相邻的虚拟节点所对应的全部路径都被访问，得到该运输网络的所有路径集合。根据路径集合每个数组中倒数第2 个节点即可确定出海港，对其适应度进行排序可得到次优选择结果。

当不考虑货物的时间价值和港口班期限制，改变货主对时间和成本的灵敏度，得到出海港路径选择结果，如表7所示。此时，佛山港的选择频率比较高，对于成本和时间的不同偏好使到港集疏运方式相应发生改变。

不考虑货物的时间价值但是考虑港口的班期限制，得到的最优出海港路径选择结果与表7的情况类似。在实际生活中，由于贸易的不确定性和可能出现的突发情况，研究次优路线十分必要。假定托运人对时间敏感度与费用敏感度相同，得到不同出发日期下考虑航运班期限制的港口选择结果如图2所示。

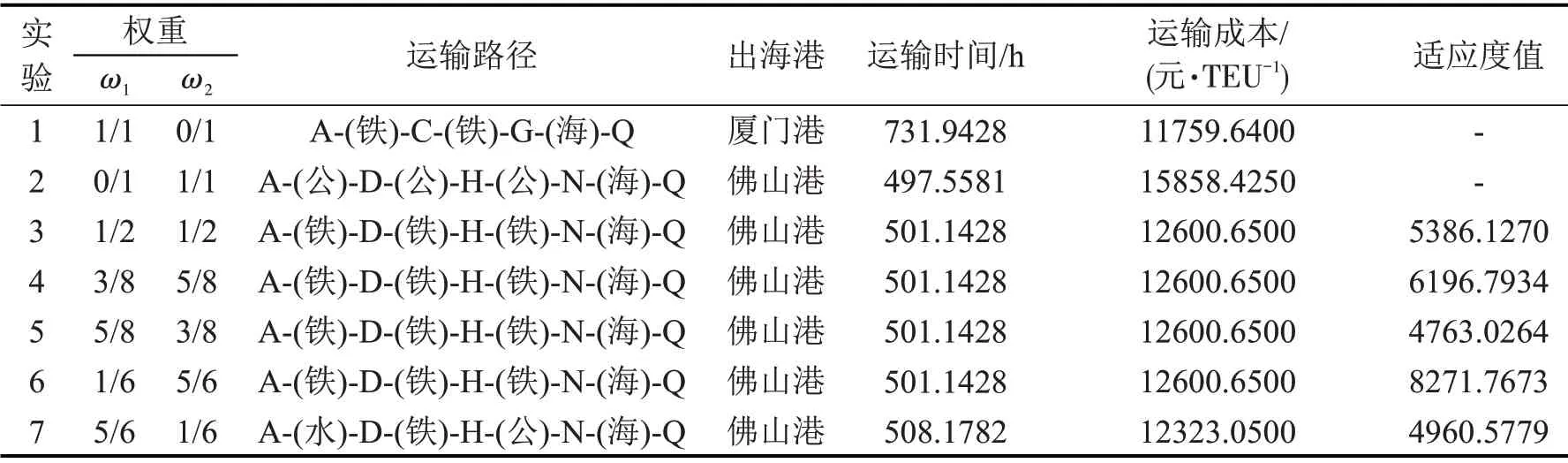
表7 考虑不同偏好的出海港最优路径选择结果Table 7 Optimal route selection results of port with different preferences

由图2可知，由于班期限制，对于次优港的选择，不同出发日差别较大。考虑选择佛山港的频率很高，这是由于长沙距离广东省很近，通达性良好，且佛山港该段时间集装箱的远洋报价十分具有竞争力，广州港虽然具有和佛山港相似的交通条件，但是，调研期内的价格吸引力远远低于佛山港。船公司在厦门港的报价虽和其他港口相比也具有价格优势，但是，从厦门出发的航期较长，拉低了价格优势，由图2(b)可知，当其他港口暂无航班通达时，厦门港的优势凸显。由于考虑了班期，时间的目标函数值有所变化，但是成本的目标函数没有变化(假设集装箱到港没有赶上班期产生的等待时间在港口的免费堆存期内)，这是偏离实际的，这是因为货物本身具有时间价值，且托运人对于不同价值的货物的敏感程度也相应有所偏差，因此，本文依据文献[3]列出4类货种中具有代表性的货物如表6所示，根据货物属性选定各自的权重，以出发日期周一为例进行迭代，得到相应的最优路径选择结果和次优港及到港路线情况，如表8和表9所示。

表8 不同货类考虑时间成本最优出海港选择结果Table 8 Optimal port selection results of different cargo types considering time cost

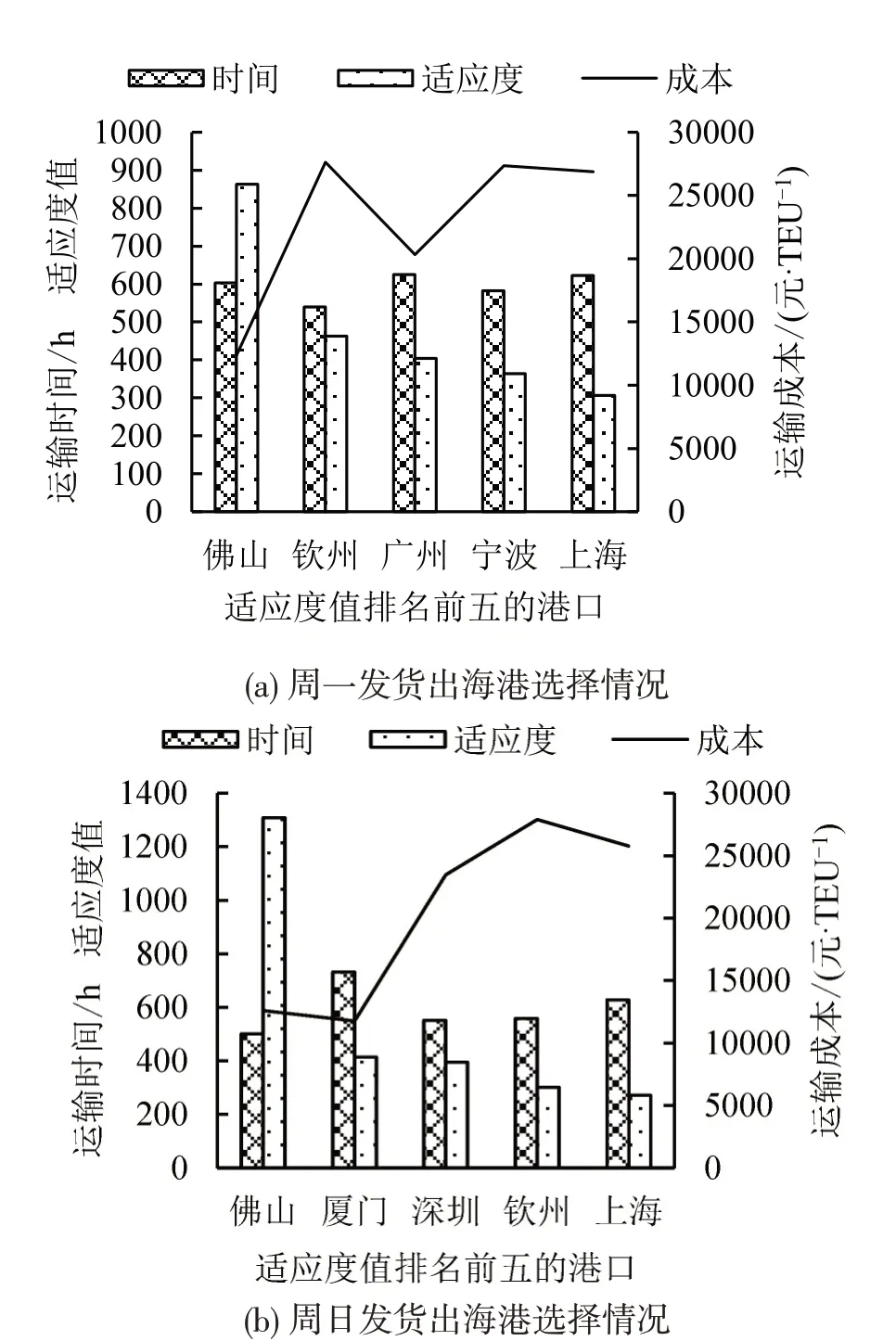
图2 长沙至德班不同出发日期选择出海港情况Fig.2 Selection of departure ports from Changsha to Durban on different departure dates

当考虑不同性质货物的时间价值时，最优的选择路径发生较大变化，出海港的选择在实验8和实验10中变成钦州港，可见，对于时间性要求高的货类且其本身价值相对不低的情况下，货主愿意选择到港成本更高的其他港口弥补原港口班期的等待。

在综合考虑货物的时间价值成本后，不同性质的细分货类的整体选择路线发生了很大的改变，不再如图2(a)所示的排名结果：佛山、钦州、广州、宁波、上海。对于高价值、高时间要求的货物，例如，笔记本电脑，佛山港的选择下降到第4，航程时间短、等待航班时间少的出海港此时具有绝对优势，且高价值货物的高时间成本拉大了这种差距，例如，此时天津港和青岛港比广州港和厦门港靠前。但是对于本身价格不是特别高昂的货类，海运价格的报价优势依旧有吸引力，例如，表9低价值、高时间敏感度中佛山港排位第2。对于本身价值较低且对运输时间要求不高的货类，海运报价优势对于托运人的吸引力更加明显，例如，表9低价值、低时间敏感度中的厦门港和广州港。

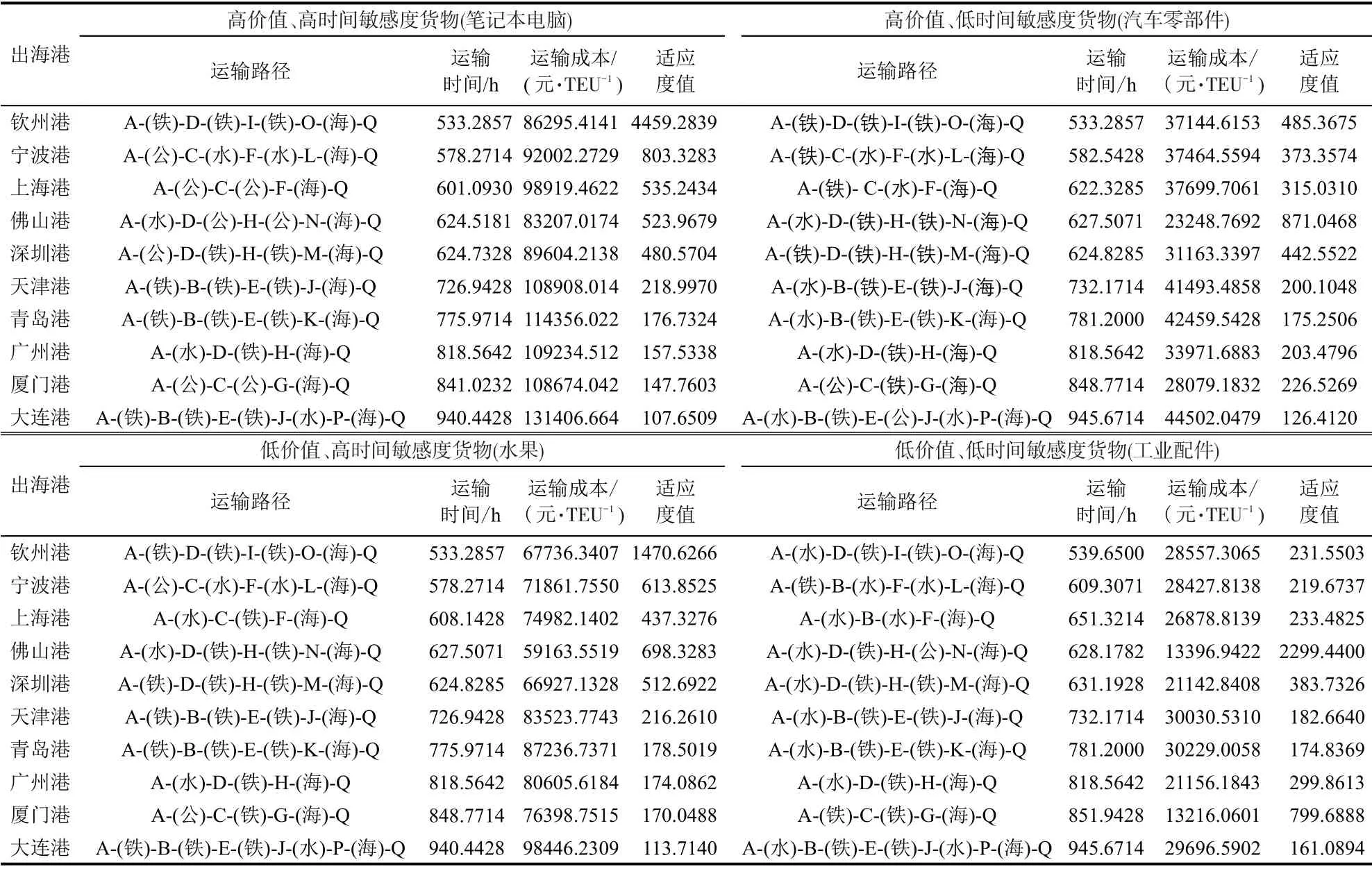
表9 不同货类次优出海港选择结果Table 9 Results of port selection for different types of goods

3.3 运输报价变化对结果的影响

在出海港路径选择问题中，国内段公路、铁路及水运的运输价格相对固定，实际应用中，船公司和货代对海运报价会随着市场供给需求有较大的波动。

以调研期内星航运(ZIM)在上海港的海运报价为基础分析算例数据，选取算例中高价值、高时间敏感度和低价值、低时间敏感度货类进行海运价格调整分析。从图3可以看到，第1 类货物由于其本身的高初始价值和较高的贬值率，产生较高的货物时间成本使最优港给货主的运输报价下调(或次优路线的到港内陆运输补贴)达到5981.19 USD·TEU-1，次优港才能与之达到同等竞争力水平，可见，高价值、高时间敏感度货物对运输费用的承受能力更大，对运输服务水平(时间)要求更高，这与文献[12]得出的结论一致。即巨大幅度的报价调整才会改变高价值、高时间敏感度货物的出海港选择，托运人对出海港的选择具有较强的鲁棒性。而对于低价值、低时间敏感度的货物，本算例中最优港给货主的运输报价下调(或次优路线的到港内陆运输补贴)达到450.79 USD·TEU-1，两者可达到同等竞争力水平。尽管已经综合考虑货物运输期内的时间成本，低价值、低时间敏感度货物的运输报价调整幅度依旧能在可控范围内，实现托运人对多个港口选择的变换。因此，在各港口开设航线的船公司可在重点满足高价值、高时间敏感度货物的运输需求情况下，灵活调节对低价值、低时间敏感度货物的海运报价，以此整合运力资源，实现收益最大化。

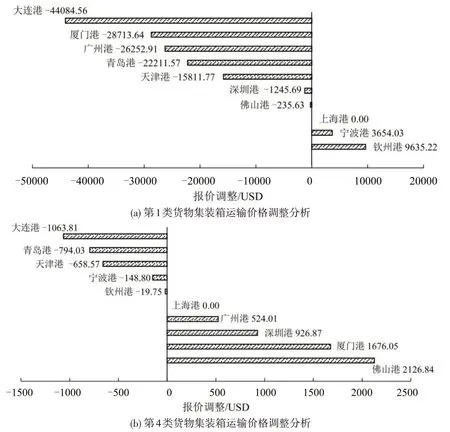
图3 不同货类海运报价调整Fig.3 Sea freight quotation adjustment analysis for different goods

4 结论

本文将货物的时间价值纳入成本，构建不同货类的中非多式联运路径及出海港选择模型。长沙至德班的算例结果表明：

(1)班轮的班期、运输报价及货物的时间价值都会影响托运人对于出海港的选择。

(2)对于时间性要求高且本身价值相对不低的货物，货主愿意选择到港运输成本更高的其他港口，弥补原港口班期的等待。

(3)托运人对于高价值、高时间敏感度货物的出海港选择具有较强的鲁棒性，本算例中，最优与最次港口成本相差高达53719.78 USD·TEU-1；对于低价值、低时间敏感度的货物，尽管已考虑运输期内的货物时间成本，海运报价的调整幅度依旧能在1000 USD·TEU-1内实现托运人对多个港口选择的变换，最优与最次港口成本相差3190.65 USD·TEU-1，具有相对的可控性。因此，船公司可在重点满足高价值、高时间敏感度货物的运输需求情况下，灵活调节对低价值、低时间敏感度货物的海运报价，以此整合运力资源。