需求不确定下的网约车司机最优工资水平研究

王景鹏，祝蕊，王鹏飞

(1.山东大学，a.管理学院，b.社会超网络计算与决策模拟实验室，济南 250100；2.燕山大学，河北省土木工程绿色建造与智能运维重点实验室，河北秦皇岛 066004；3.河北科技师范学院，秦皇岛市交通系统智能分析与决策重点实验室，河北秦皇岛 066004)

0 引言

伴随着移动互联技术和GPS 定位技术的快速发展，基于需求的网约车出行发展迅猛。网约车出行模式通过盘活社会闲置资源，将寻求出行服务的乘客和愿意提供服务的司机连接在一起，提高了交通系统的运行效率。

国内外关于网约车出行系统乘客收费和司机工资机制设计的研究有很多。BAI 等[1]研究了收费-工资对于价格敏感型乘客和工资敏感型司机的影响，并探讨当出行平台最大化利润时的收费-工资机制。TAYLOR[2]研究乘客等待时间参数的不确定性对网约车系统中收费和工资水平的影响。BIMPIKIS 等[3]研究交通网络中的空间收费对网约车平台利润的影响。依据传统的瓶颈模型，WANG等[4]研究了合乘出行下的司机-乘客间的收费-工资机制设计问题。针对高峰时需求激增现象，YANG 等[5]从司机工资层面设计了红包奖励机制。研究发现，在某些情况下，乘客、司机以及平台都会受益。对共享出行中乘客收费和司机工资水平设计的研究，WANG 等[6]做了总结性的评述。另外，很多学者还从运作管理的角度，将收费-工资研究扩展到了以网约车出行平台为代表的一般化的按需服务平台，例如，YU 等[7]和WANG 等[8]。赵道致等[9]研究不同监管目标的网约车服务价格管制策略；在考虑等待时间的基础上，赵道致等[10]研究了网约车与出租车的均衡定价问题；彭向等[11]基于社会福利最大化，研究网约车平台定价机制设计。除此之外，在共享汽车领域，王宁等[12]分析了动态定价对消费者取车、还车行为的影响机制，构建动态定价机制下共享汽车自适应调度模型。

但是，现有研究大多假设在当前时段网约车平台获知了准确的乘客出行需求，在此基础上，进行相应的收费和司机工资水平策略研究[1-3]；或者假设工资是收入的固定比例。然而，现实中乘客需求具有极大的不确定性。网约车平台只有在时段末端才能获知全部的乘客需求，如果此时再制定司机工资水平，吸引数量足够多的司机提供出行服务，则具有一定的时间滞后性，很难满足即时乘客需求，从而导致乘客取消订单，降低交通系统的运行效率。而且，固定比例的工资机制过于保守和僵化，平台很难调控供需关系。

因此，本文研究的主要问题是：在乘客出行需求不确定的情况下，以利润最大化为目标的网约车平台如何制定司机工资水平，才能够吸引足够数量的司机提供出行服务。本文对乘客出行需求不确定性问题进行方法论研究，给出最优工资水平的建模思路和求解框架，并在此基础上分析司机工资水平。

1 模型构建

考虑网约车出行系统的现实特点，对模型做出以下假设：

假设1 某一时段内，当平台制定乘客收费标准时，会预估得到乘客最大出行需求。

假设2 某一时段内，每个乘客只能完成单次出行，乘客出行具有同质性。

假设3 某一时段内，乘客出行需求数量随机分布，但其概率分布函数已知。

假设4 为吸引更多网约车司机提供出行服务，平台提供更高的工资水平；司机的服务速度为1，即单位时段内每个司机服务一个乘客。

以上4个假设符合现实场景。实际工作中，网约车平台通过早高峰时段上调车费，普通时段降低费用，一方面鼓励错峰出行，减少拥堵；另一方面，平台调控了出行市场需求-供给关系，使需求与供给得到更好的匹配。在不同时段，平台对乘客的收费与最大乘客需求呈现动态性；而在某一具体时段内，收费与出行需求呈现确定性关系。虽然，网约车平台通过历史数据挖掘等方法获知某一时段的乘客最大出行需求，但由于出行需求的随机性，平台事前无法获知准确的出行信息。与文献[1]、文献[2]及文献[7-8]一致，本文假设在某一时段内，乘客只能完成单次出行，且出行活动具有同质性(相同的出行距离)。将出行距离异质化虽然可能带来新的分析亮点，但将增加问题处理的复杂度。为分析方便，本文假定出行距离是同质的。司机根据网约车平台提供的工资水平决定是否提供出行服务。一般而言，工资水平越高，司机越有意愿提供出行服务；反之，则不然。为吸引足够数量的司机提供搭乘服务，网约车平台需要提供足够高的工资水平。

令pi,Qi,xi,wi,ki,qi分别代表i时段的乘客收费、最大乘客需求、随机到达的乘客数量、司机工资水平、愿意提供服务的司机人数以及乘客-司机匹配率。为便于标记，在后面的分析中，统一省略下标i。

根据假设4，当工资水平上升时，会有更多的网约车司机提供服务，即司机为追求收入最大化，只考虑替代效应而不考虑收入效应。根据劳动供给理论，假设某一时段内，网约车出行系统中愿意提供服务的司机人数k是工资水平w的增函数，即

式中：K为愿意提供出行服务的最大司机数量；w为某时段内网约车平台提供给司机的工资水平，满足，即为使得更多的司机有意愿提供服务，平台需要提供更高的工资水平。

用x表示某一时段的乘客真实出行需求；F(·)表示累积概率分布函数，满足：F(0)=0，F(∞)=1；f(·)表示乘客出行需求的概率密度分布函数。尽管某一时段内乘客真实出行需求存在不确定性，但网约车平台可以通过历史数据挖掘等多种方法预测乘客出行需求分布函数。假设每个乘客只能完成单次出行，则司机的服务速度为1，即在每时段内，每个司机只能服务一个乘客。乘客真实出行需求x是一个随机变量，既可能大于愿意提供服务的司机人数k(此时，部分出行需求不能被满足)，也可能小于愿意提供服务的司机人数k(此时，所有出行需求都能被满足)。

与文献[8]一致，本文采用“一对一”精准匹配表述供给-需求匹配函数，某一时段匹配成功的乘客-司机数量由该时段的乘客需求和车辆数的最小值决定，即匹配率是乘客出行需求与司机服务供给的最小值，计算公式为

当网约车出行系统达到均衡时，在给定的工资水平w下，愿意提供出行服务的司机不会退出网约车出行系统，即均衡下的司机人数为k。对于随机到达的乘客出行需求x，网约车平台利润函数为

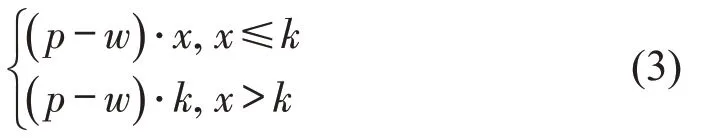
式(3)给出不同情形下的网约车平台利润。研究发现，乘客出行需求会影响网约车平台的利润。由于网约车平台的目标是考虑需求随机性下的利润最大化，因此，其目标可以被描述为数学规划问题，即

服从于

定理1 最优化问题至少存在一个最优解。

证明：由于式(4)目标函数的连续性，且决策变量w的可行集是紧的闭集，因此，最优化问题式(4)至少存在一个最优解。

2 网约车出行系统均衡

在乘客出行需求服从均匀分布的特殊情形下，分析式(4)的解析性，目的是为了得到封闭解，探索乘客出行需求不确定下网约车出行系统的均衡性质。

基于假设1，最大乘客出行需求Q是基于时段的。当时段划分较为密集时(例如，每0.5 h 为1 个时段)，可以认为乘客出行需求服从0～Q之间的均匀分布：x～U[0,Q]。

由于司机追求收入最大化，在不考虑收入效应的前提下，更高的工资水平会导致更多的司机提供出行服务。根据式(1)，假设愿意提供服务的司机人数k是关于工资水平的线性增函数，即

式中：愿意提供出行服务的最大司机数量K满足K≥Q，表示愿意提供出行服务的最大司机数量大于乘客最大出行需求，现实中潜在的司机数量确实远大于乘客出行需求；η为固定参数，η越大，表示工资水平的每单位增加值会导致更多的司机提供出行服务，司机供给曲线越陡峭，因此，参数η客观反映了网约车平台对出行系统中司机的影响力。现实中，影响力可以反映在平台的市场垄断力量和司机对平台的依赖度等。一般来说，平台的市场份额越大，垄断程度越大，其影响力越高。在其他条件相同的情况下，市场份额较大的网约车平台可以获得更高的利润。在市场培育初期，许多网约车公司为了获取较大的市场份额而给司机提供补贴，目的是吸引较多的自驾车司机加入网约车系统中，从而占据较大的市场份额，获取一定的垄断力量；当市场较为成熟时，用户对于某网约车平台的接受认可程度较高，用户黏性度较高，其影响力增强，工资水平的每单位增加值会导致更多的司机提供出行服务。当影响力足够高时，可能呈现出“店大欺客”的社会现象。由式(6)得到k≤K，即

证明：反证法。假设网约车平台目标最优时k＞Q，即，网约车平台期望的提供服务的司机数量大于乘客最大出行需求，此时，网约车平台可以通过降低工资水平而减少司机数量，达到增大利润的目的。因此，必然有k≤Q。由式(6)得到

由于K≥Q，因此，网约车平台目标最优时有

将式(6)代入式(4)，网约车平台的利润函数为

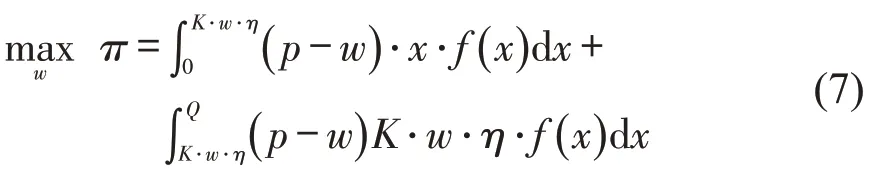
最优情况下，由一阶最优性条件得到

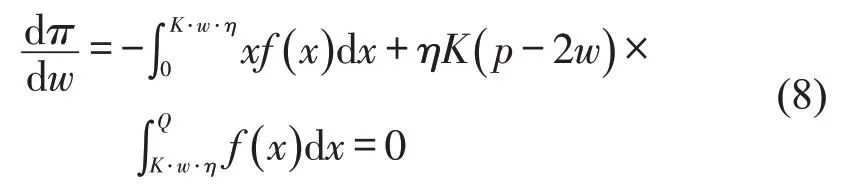
由此可得

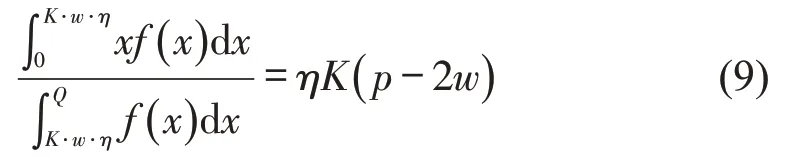
由式(9)可知，此时，需要满足不等式p-2w≥0成立，即因此，结合定理2，得到最优工资水平约束为

由于假设乘客出行需求服从均匀分布x～U[0,Q]，故f(x)=，关系式为

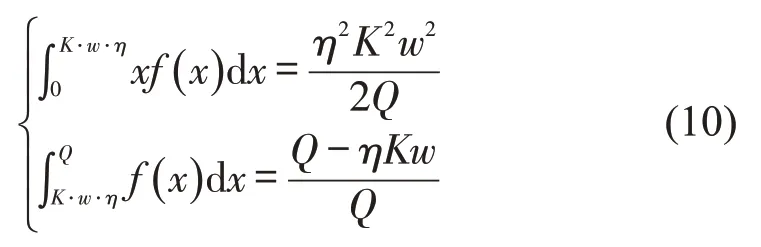
将式(10)代入式(9)可得

将式(11)展开，为了求得最优解，需求解方程，即

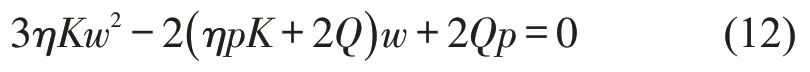
上述关于w的一元二次函数的两个解w1,w2分别为

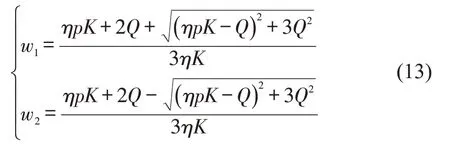
当ηpK≥Q，得到；当ηpK＜Q，得到，因此，一元二次函数式(12)存在唯一最优解w*=w2。

此外，由于w2=，因此，当当ηpK＞因此，最优解w*=w2，满足式(9)中的要求。

由此得到乘客出行需求服从均匀分布下的司机最优工资水平和愿意提供出行服务的司机数量。研究发现，存在最优的最优工资水平w*使得网约车平台利润最大，其值与参数η、p、K、Q相关，可以指导网约车平台制定司机工资水平。根据本文提出的模型，网约车平台可以获得给定参数η、p、K、Q下的最优工资水平w*和愿意提供服务的司机数量k*，获知平台的最大利润。

3 参数敏感性分析

敏感性分析考察乘客最大出行需求Q和网约车平台对司机影响力的变化对最优工资水平w*和司机人数k*的影响。

定理3 在其他参数不变的情况下，随着乘客最大出行需求的增加，司机工资水平增加，愿意提供出行服务的司机数量增加。

证明：将最优工资水平w*和愿意提供服务的司机数量k*对最大乘客需求Q取一阶导数，得到

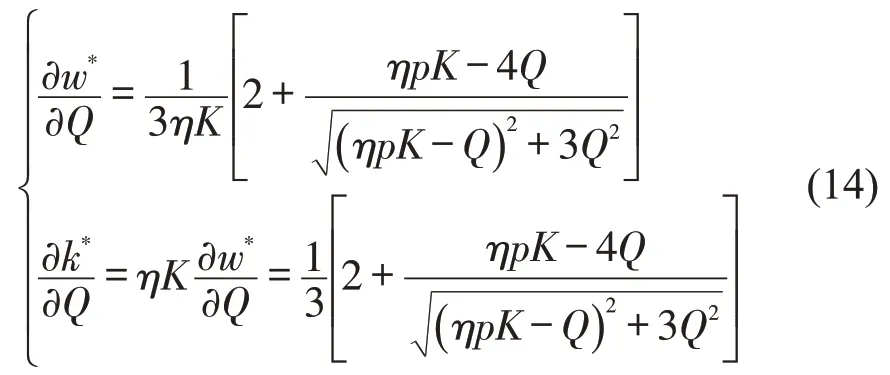
(1)如果ηpK≥4Q，得到

(2)如果ηpK＜4Q，则有

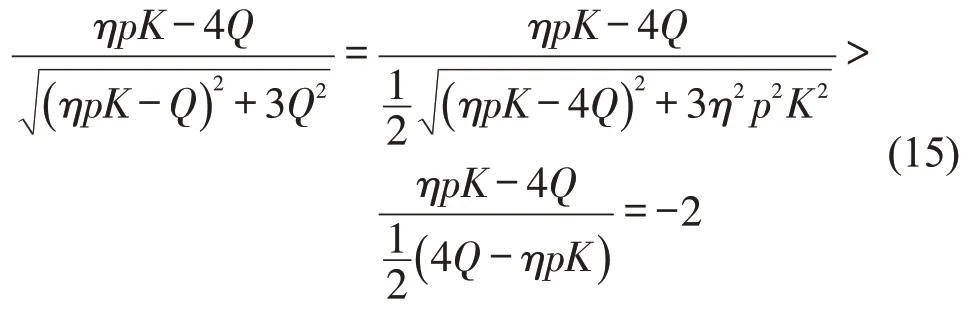
因此，无论ηpK与4Q大小关系如何，最优工资水平与司机人数都随着乘客最大出行需求Q的增大而增大。

定理3 说明，在乘客最大出行需求比较大的早、晚高峰期间，网约车平台可以适当调高司机工资水平，调动更多的司机提供出行服务，获得更高的利润；在乘客最大出行需求比较小的时段，网约车平台可以适当降低司机工资水平。

定理4 在其他参数不变的情况下，随着网约车平台对司机影响力的增强，司机工资水平降低，愿意提供出行服务的司机数量增加。

证明：将最优工资水平w*和愿意提供服务的司机数量k*对网约车平台影响力参数η取一阶导数，得到

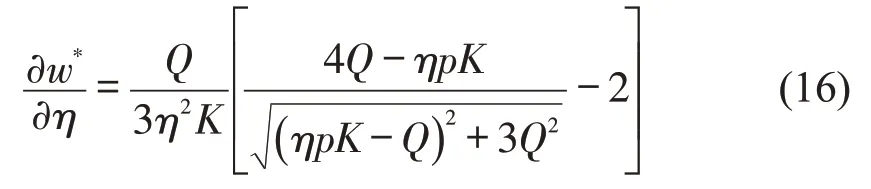
(1)如果ηpK≤Q，得到

(2)如果ηpK＞Q，则有，得到

定理4说明，网约车平台可以通过提高自身的影响力降低司机工资水平并增大利润。

研究发现，愿意提供服务的司机数量k*对参数Q、η正相关，最优工资水平w*对参数Q正相关，对参数η负相关。

4 平均值模型

分析平均值模型下网约车系统司机最优工资水平以及愿意提供出行服务的司机数量，并与前述所建模型作对比分析。

在乘客出行需求服从均匀分布的情况下，x～U[0,Q]，其概率密度函数。基于平均值模型，网约车平台估计的乘客出行需求为此时，网约车平台的收益函数需要根据Q分别讨论。

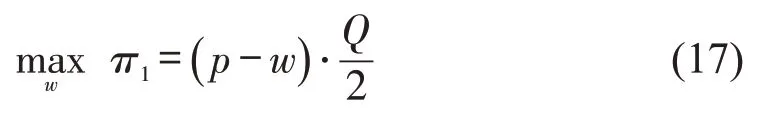
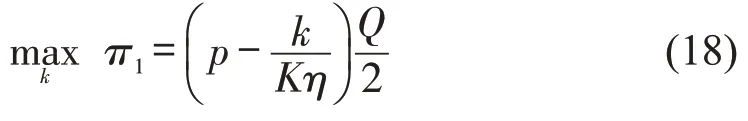
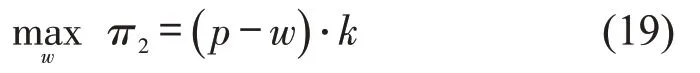
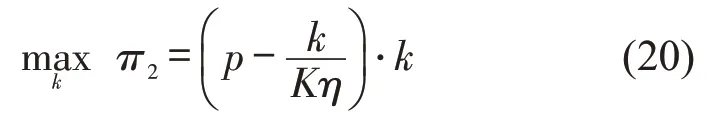
以上问题的最优解需要分情形讨论：

因此，平均值模型下平台的最优策略为

当Q≤ηKp时，有

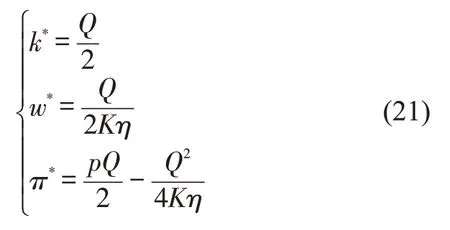
当ηKp＜Q≤K时，有

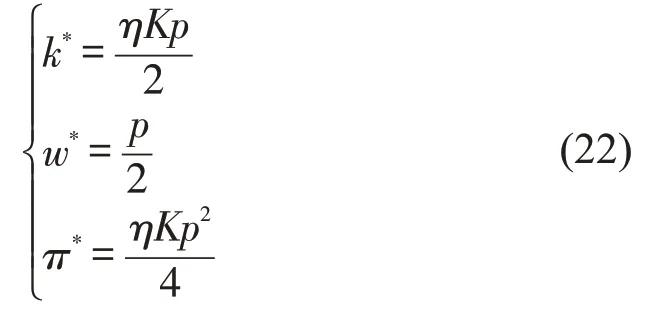
相较于本文提出的模型，平均值模型下，乘客出行需求为最大需求的1/2，这只是平台对于出行需求的预估，只代表了1 种可能情形，并未考虑实际交通系统中出行需求的随机性，例如，由极端恶劣天气、大型集会活动等突发事件导致的需求激增现象。因而，平均值策略中条件的成立依赖于概率。本文提出的模型，给出期望利润最大化下的最优解，相较平均值模型具有一定的鲁棒性。因此，对于网约车平台而言，本文提出的模型能够更好地刻画现实，是一种考虑较为稳妥、风险中性的策略。

推论1 当ηKp≤Q≤K，平均值模型下司机工资水平和愿意提供出行服务的司机数量要比本文模型中相关数值大。

5 数值实验

利用两个数值算例进一步验证本文的结论。利用从滴滴出行获取的2017年5月海口市的出行数据集，得到工作日每1 h 段的平均订单数据，如图1所示。

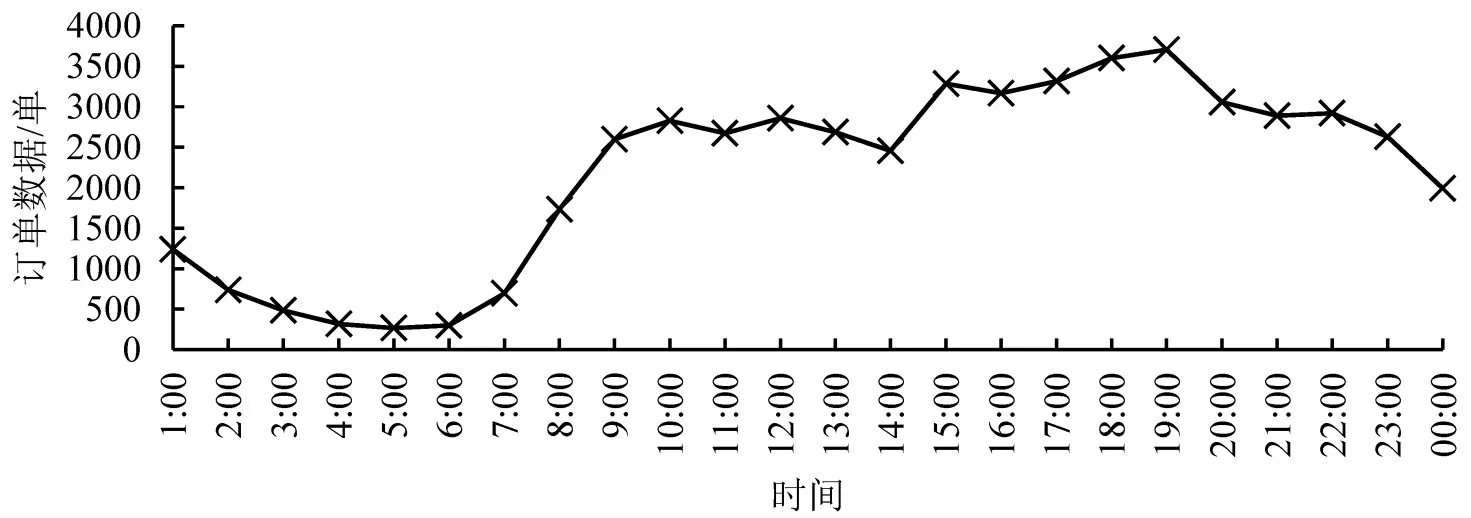
图1 工作日订单数据Fig.1 Trip order for working day

由图1可知，出行需求存在早、晚高峰的潮汐现象，一天之中出行需求变化较为剧烈，峰值为2772单，谷值为230单。

算例1 主要为验证定理3 的结论，即最优工资水平和司机人数与最大乘客需求正相关。由于缺乏最大出行需求数据，因此，将每小时的最大出行需求设为图1出行数据集中的订单数据，设p=20元，η=0.05，K=3000。司机工资水平及愿意提供服务的司机人数变化如图2所示。

由图2可知，司机人数、工资水平与最大出行需求呈现相同变化趋势，验证了定理3的结论。且曲线变化更加平缓，司机人数和工资水平的变化幅度更小(司机人数峰值为1245单，谷值为220单；工资水平峰值为8.3元，谷值为1.5元)，说明本文提出的模型综合考虑了波峰与波谷出行需求，平滑了司机工资水平与司机供给关系，有效保障网约车平台利润，具有一定的鲁棒性。

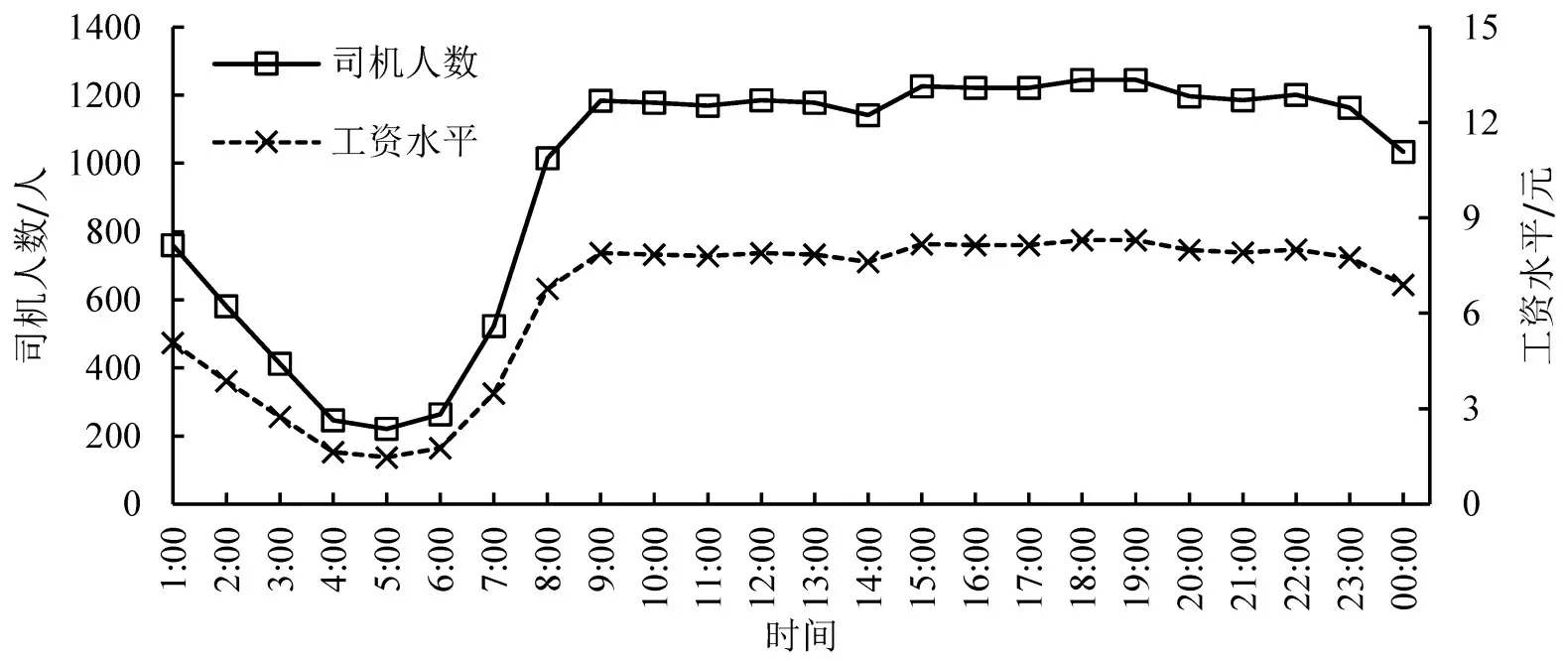
图2 司机人数与最优工资水平变化Fig.2 Number of drivers and optimal wage level

算例2 主要为考察网约车平台影响力变化对工资水平和愿意提供服务的司机数量的影响。设K=3000 人，p=20 元，Q=2000 人，网约车平台影响力η在0.00～0.10之间变化，如图3所示。

由图3可知，随着网约车平台影响力的增加，司机工资水平降低；而愿意提供服务的司机人数却增加，验证了定理4的结论。

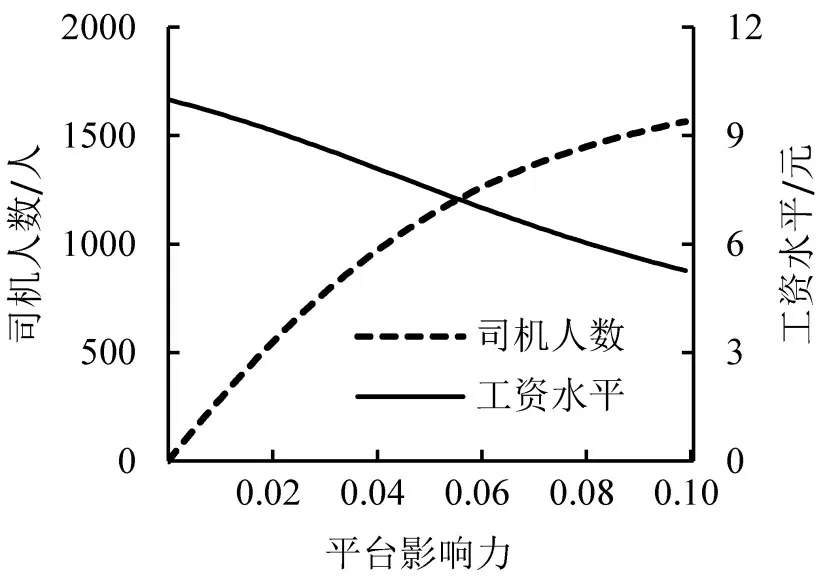
图3 司机人数与最优工资水平变化Fig.3 Number of drivers and optimal wage level

6 结论

在乘客出行需求不确定的背景下，本文给出求解网约车平台利润水平的建模思路和求解框架。由于需求函数和劳动力供给函数具有一般性，模型得不到封闭解，因此，本文给出解的特例：假设乘客出行需求服从均匀分布，且愿意提供服务的司机人数是关于工资水平的线性增函数。在此假设下，本文进行分析并做了数值算例研究。得出如下结论：

(1)本模型综合考虑波峰与波谷出行需求，平滑了司机工资水平与司机供给关系，有效保障网约车平台利润，给出了期望利润最大化下的最优解，相较于平均值模型具有一定的鲁棒性。

(2)最优工资水平随最大出行需求动态变化，在优化网约车平台利润的同时，有效调控司机供给数量，平衡波峰、波谷时需求。

(3)网约车平台的市场影响力间接影响司机工资水平设定。影响力越大，工资水平越低。