基于混合约束自编码器的机动车工况智能构建方法

林建新，刘博，赵霞，张蕾

(北京建筑大学，a.土木与交通工程学院；b.电气与信息工程学院，北京 100044)

0 引言

汽车行驶工况[1]对车辆污染物排放研究和绿色低碳发展等方面具有重要的研究价值[2]。美国最早投身于汽车行驶工况的研究[3]。此后欧洲、日本等国家也逐渐开展工况研究工作[4]。我国目前参考欧洲工况数据制定相关法规，而国内道路条件、交通条件、甚至驾驶行为特征与国外差异较大，导致车辆实际行驶过程的平均速度、怠速时间比等特征参数与国外认证标准差距较大。近年来，国内外对于行驶工况构建的研究逐渐增多。李洋等[1]将聚类算法与马尔科夫链相结合构建行驶工况。ZHANG等[5]基于改进马尔科夫链构建了电动汽车行驶工况并通过工况测算了电车能源消耗。MAYAKUNTLA等[6]用“行程段”取代传统的短行程基本单元构建了新型的汽车行驶工况。NOURI等[7]提出基于空间特征的短行程分类法，结果表明，相比其他短行程法其构建了更具代表性的工况。HE等[8]利用实时更新的交通信息重构行驶工况，进一步反映了实时交通运行状态。大部分研究采用基于降维-聚类的短行程分类法构建行驶工况，但此类方法基于随机选择合成工况，导致构建工况的随机性较强、误差不稳定。为此，研究以实际采集机动车行驶数据为数据源，通过降维和聚类划分运动学片段库，在聚类中心一定距离内随机选取与拼接构建工况集合，择出与原始数据特征参数误差最小的工况作为初步行驶工况，提出通过混合约束自编码器对初步行驶工况进行智能优化的方法，减小了随机性带来的误差不确定性，并对自编码器的优化策略进行分析验证。

研究提出了基于混合约束自编码器的机动车行驶工况智能构建方法，能够用于多源数据的解析并构建代表性的行驶工况。通过科学方法和智能科技技术推动低碳发展，对碳达峰的机动车碳排放预测具有重大的意义，为实现“双碳”目标作出积极贡献。

1 数据处理

1.1 数据采集

通过行车记录仪采集福州市某辆轻型汽车在实际城市路网上的行驶数据，如图1所示，行驶范围是福州市内不同等级、功能和区位的道路。数据包含同一车辆在14 个工作日及6 个非工作日的6:00-24:00 中不同时间段的行驶数据，选取时段包含各个高峰与平峰时期。研究获取了车辆在城市路网行驶过程中的时间、速度、发动机转速、经度、纬度共5项指标，采样间隔为1 s。

图1 车辆全部行驶轨迹覆盖图Fig.1 Coverage map of all vehicle trajectories

1.2 数据预处理

数据采集过程中，由于采集设备本身或周围环境导致信号较弱，造成数据异常或丢失。数据不恰当处理，会严重降低数据质量与可靠性。具体数据处理流程如图2所示。

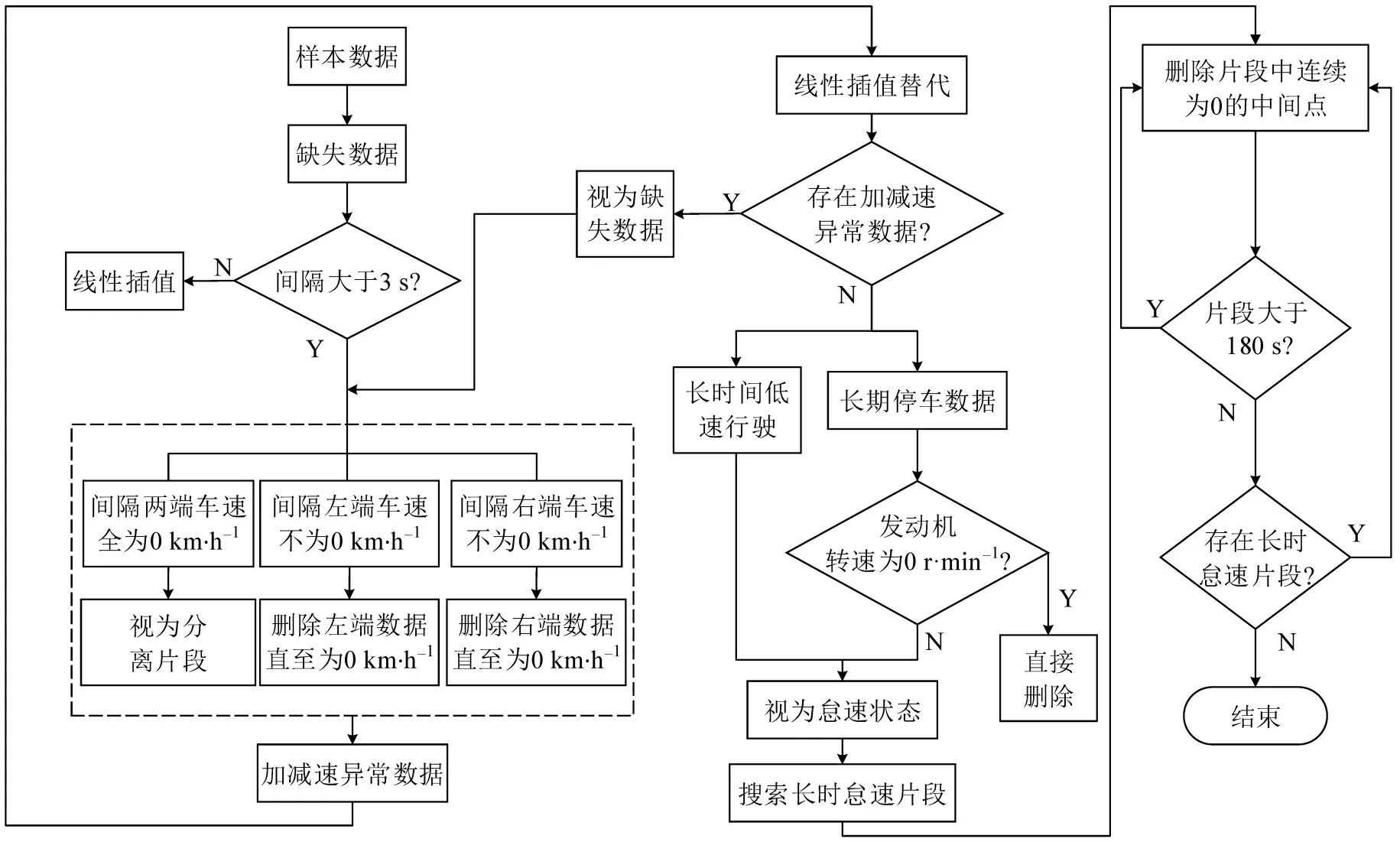
图2 数据处理流程Fig.2 Flow chart of data processing

(1)缺失数据填充

对于缺失数据时间间隔大于3 s 的情况：如果间隔两端车速全为0 km·h-1，视为分离片段；如果间隔左端速度不为0 km·h-1，则删除左端数据直至速度为0 km·h-1；如果间隔右端速度不为0 km·h-1，则删除右端数据直至为0 km·h-1；对于缺失数据间隔小于3 s 的情况，采用线性插值将不连续数据连接起来[9]。

研究认为普通轿车0～100 km·h-1速度下加速度大于4 m·s-2或减速度大于7.5 m·s-2时为异常值[9]。通过异常点周围数据进行线性插值替代处理，如果处理后仍然存在加速度异常数据，则说明异常点周围数据也为异常数据，直接按照缺失数据处理。

(3)长期怠速数据

对于长期车速为0 km·h-1的数据，如果发动机转速为0 r·min-1，表示发动机处于熄火状态，则直接删除数据；如果发动机转速不为0 r·min-1，视为怠速状态。将长时间(超过180 s)低速行驶状况(车速小于10 km·h-1)也视为怠速状态。对搜索到连续怠速时间大于180 s 的工况，逐个删除片段中连续为0 km·h-1的中间点，直至怠速时长为180 s用于工况的构建。

2 运动学片段提取

2.1 运动学片段的定义

目前分析海量车辆行驶数据主流方法是将全部的时间-速度数据划分成若干个运动学片段。运动学片段指车辆从怠速状态至相邻下一个怠速状态开始的运动过程，通常包括怠速、加速、减速、匀速部分，由于车辆在不同的道路条件、交通环境下会展现出不同的行驶特征，导致运动学片段的速度分布呈多样性，因此，研究通过随机组合各类运动学片段描述车辆的行驶过程，将划分的短时片段聚类，构建符合实际情况的行驶工况。

2.2 运动学片段的划分

研究将全部时间-速度数据划分为多个“怠速-行驶-怠速”的运动学片段。由于数据采集终端的信号问题，会出现车辆没有从速度为0 km·h-1起步或者片段结束点速度不为0 km·h-1，将其视为错误数据并直接删除。通过对运动学片段的遴选，最终划分运动学片段1445个，总共数据量为198434条。

2.3 特征参数选取与计算

受道路交通状况影响，运动学片段之间差异显著。不同运动学片段反应车辆不同的行驶状态，为更好地通过组合的运动学片段描述车辆的运动过程，选取合适的特征参数评价。在查阅相关文献基础上[1]，选取14个特征参数，如表1所示。

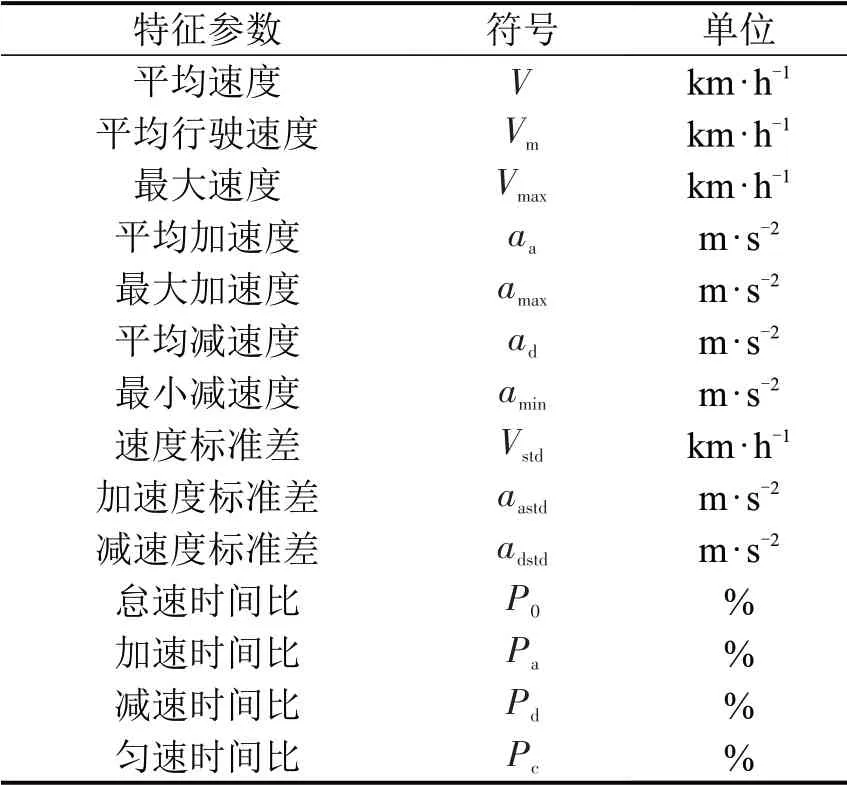
表1 特征参数Table 1 Characteristic parameters

计算各个运动学片段的14 个特征参数，作为后续运动学片段分类的依据，并为行驶工况的构建提供评价标准。

根据以上初步的配合比（02号）中水胶比和砂率按《水工混凝土试验规程》（SL352-2006）规定进行调整，水胶比增减0.05、砂率相应增减1%，得出01和03号调整后的配合比进行试配，如表6共3个配合比进行试配，表7为3组配合比试配后得出各项混凝土性能指标。

3 机动车行驶工况构建

3.1 构建流程

为简化计算，通过主成分分析法对特征参数进行降维，采用K-means 聚类法进行运动学片段分类，取各聚类中心距离最近的30 个运动学片段进行随机组合，构建工况集合，并选取误差最小的工况作为构建工况，如图3所示。

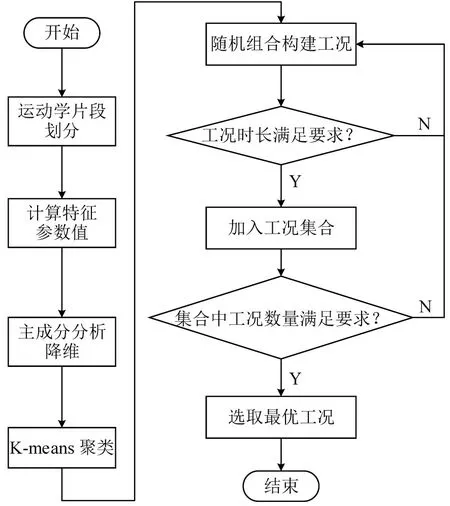
图3 机动车行驶工况构建流程Fig.3 Flow chart of construction of vehicle driving cycle

3.2 主成分分析降维

调用Python中的数据降维库，使用其中的PCA函数对标准化后的特征参数值进行降维。设定超参数n_components 为0.9，即选取累计贡献率达到90%的主成分，基本涵盖全部信息。最终选取5 个主成分表征全部特征参数。因子载荷矩阵计算结果如表2所示，主成分1 表达了平均速度、最大速度、平均行驶速度、速度标准差、加速时间比和最小减速度；主成分2表达了怠速时间比、平均加、减速度和加、减速度标准差；主成分3 表达了减速时间比；主成分4表达了最大加速度；主成分5主要表达了加速时间比。

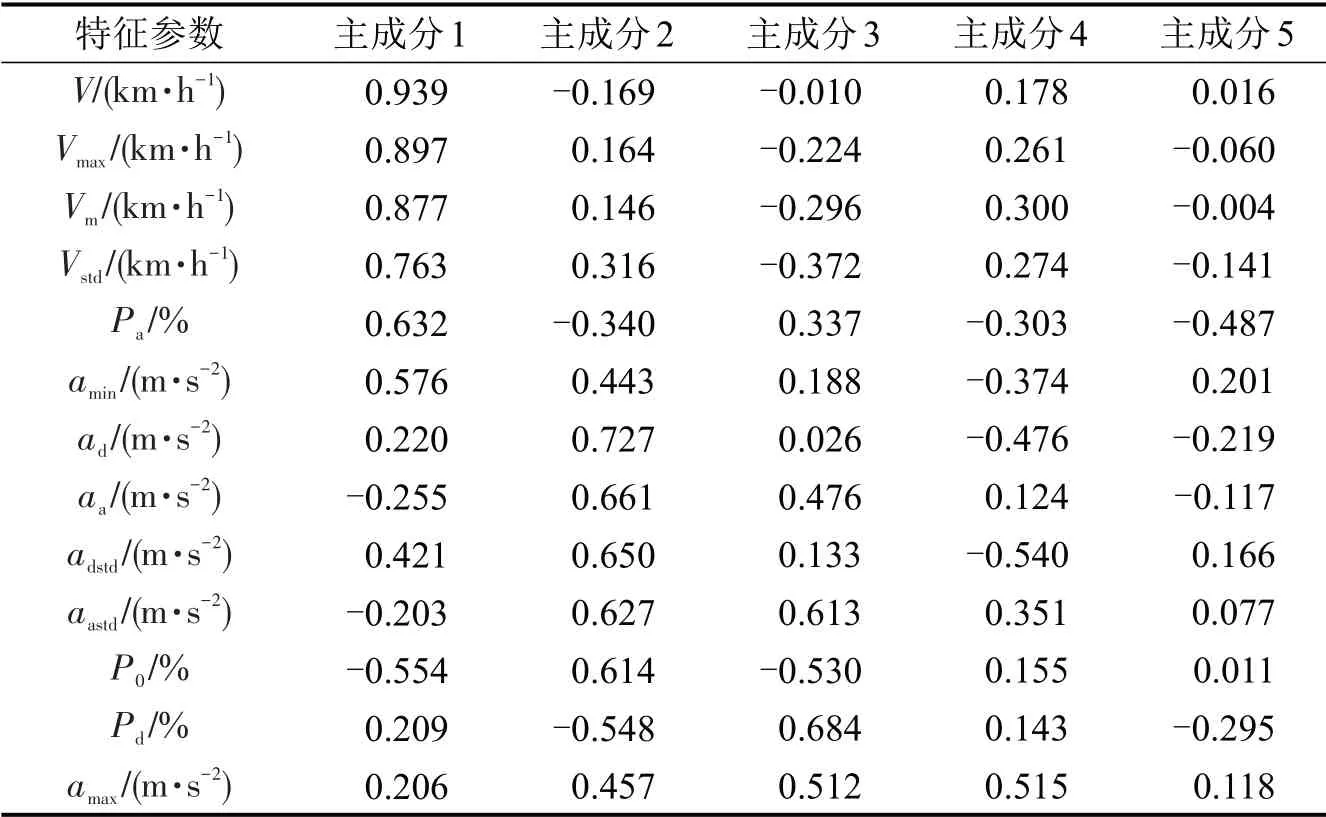
表2 运动学片段的因子载荷矩阵Table 2 Factor load matrix of kinematic segment

3.3 运动学片段聚类

通过K-means 聚类算法将运动学片段分类。调用Python中的数据聚类库，使用K-Means函数对降维后的主成分进行聚类处理，选取Calinskiharabaz分数[10]作为评价指标，解决评估分类的合理性，分别计算不同分类下的Calinski-harabaz 分数值，计算公式为

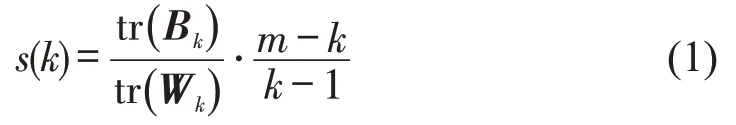
式中：m为样本总量；k为分类的数量；Bk为簇间协方差矩阵；Wk为簇内协方差矩阵；tr 为矩阵的迹。

s(k)分数越大，类别内部数据的协方差越小，聚类效果就越好。计算不同聚类数的s(k)值，如图4所示，验证表明聚类数为3时最合理。

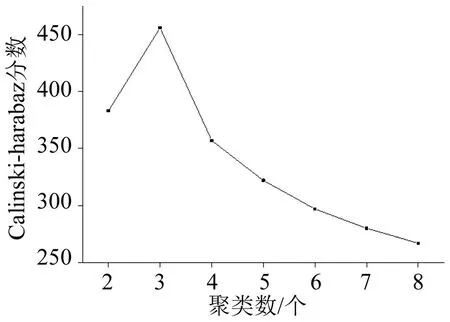
图4 聚类数量折线图Fig.4 Line chart of number of clusters

将1445个运动学片段划分为3类，聚类结果如图5所示。第1类、第2类和第3类运动学片段数分别为581、362和502个。计算各类运动学片段的特征参数值，结果如表3所示。从聚类结果来看，第1类圆形图标运动学片段平均速度最低，怠速时间比很高，平均加速度、减速度均较大，表征了较为拥堵的城市支路运行模式；第2类矩形图标运动学片段平均速度和怠速时间比适中，表征了城市主干道的中速行驶特征；第3类三角形图标运动学片段平均速度最大，怠速时间比最小，表征了快速路的高速运行特征。

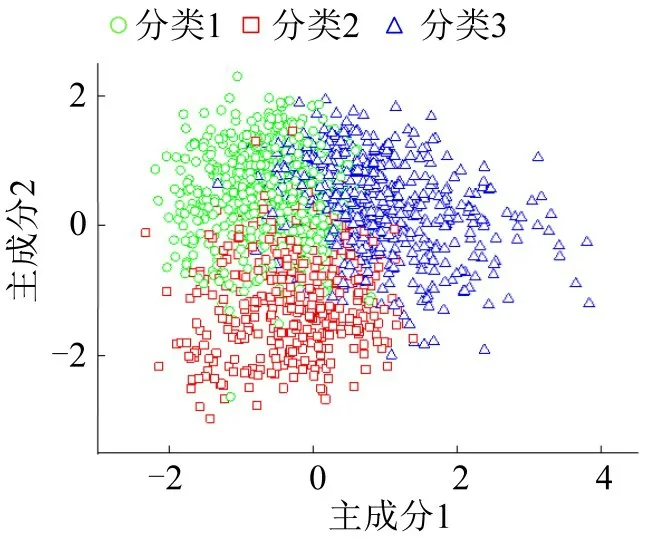
图5 全部运动学片段的聚类Fig.5 Clustering of all kinematic segments

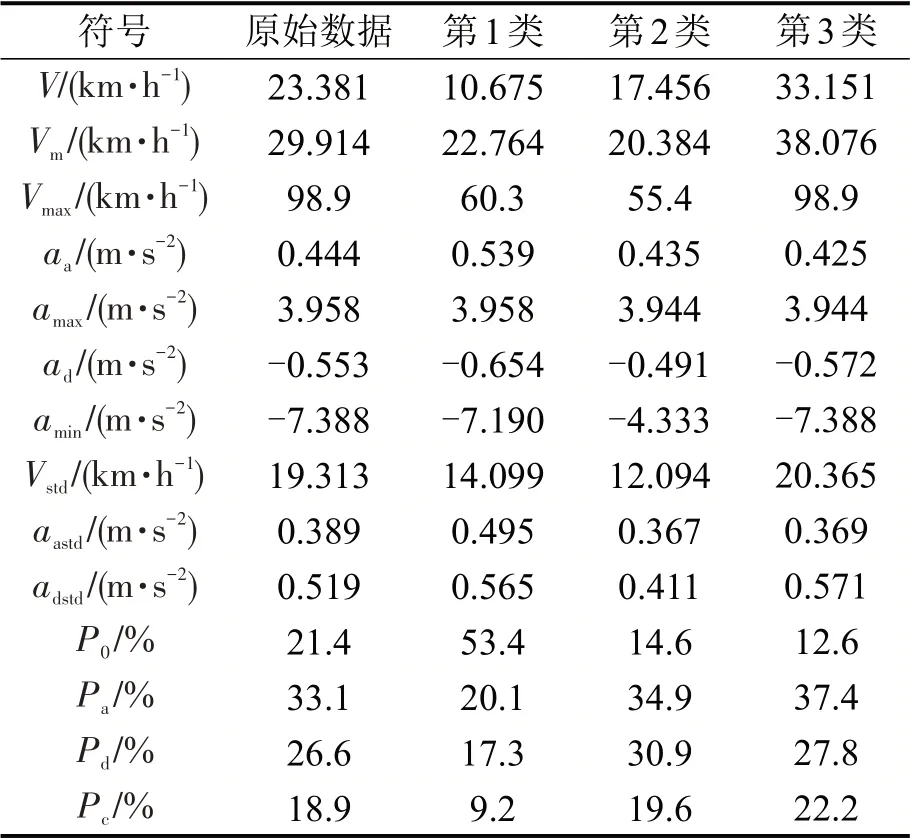
表3 3类运动学片段的数据特征值Table 3 Data eigenvalues of three types of kinematic segments

3.4 行驶工况的构建

(1)行驶工况合成

式中：Ni为构建工况包含第i类运动学片段数量；Ti为第i类运动学片段总时间；Ts为全部运动学片段总时间；Dt为期望工况时长，已有研究表明行驶工况长度取决于全部收集数据的短行程片段的平均长度[7]，考虑到本文短行程片段的平均长度为137 s，最终设置期望工况时长为1300 s；ti为第i类运动学片段平均时长。

各类运动学片段总时间分别为105305，30474，62655 s，将1300 s 设定为工况时长期望值，则各类运动学片段占行驶工况的时间分别为689，200，410 s，最终根据式(2)确定构建工况包含第1 类、第2类和第3类运动学片段分别为4，2，3个。

将各类距离聚类中心最近的前30个运动学片段作为备选片段，根据各类片段数量要求随机抽取备选片段合成行驶工况，筛选时长在1200～1300 s内的工况加入工况集合，创建大小为400的工况集合。由于数据采集车辆行驶过程中可能受到个别事件影响，导致构建工况与原始数据间的最大速度和最大加、减速度误差过大，综合实际，考虑不适合作为构建工况的评价指标，选取其余11 个特征参数构建评价体系。取集合中与原始数据相对误差最小的工况作为构建工况。

(2)工况合成分析

如图6所示，按照工况合成方法，构建时间长度为1275 s 的机动车行驶工况(简称工况1)，与原始数据的平均相对误差为2.97%。对比工况1与原始数据的特征参数，如表4所示，加速度标准差和匀速时间比相对误差分别为6.43%和5.82%，其余特征参数相对误差均在5%以内。

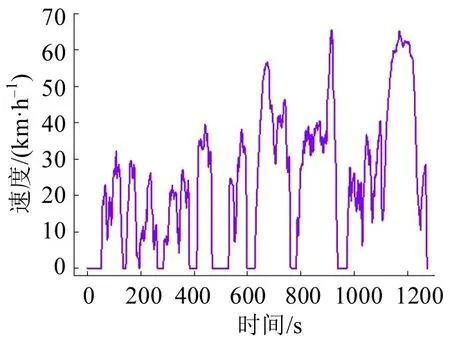
图6 工况1时间速度曲线Fig.6 Time-speed curve of driving cycle 1

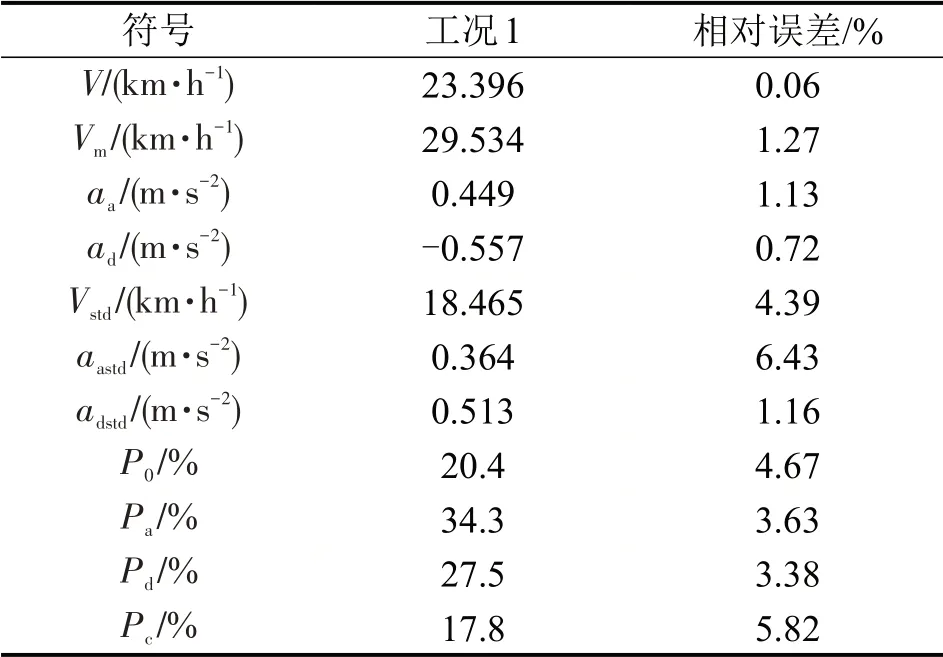
表4 特征参数对比分析表Table 4 Comparative analysis table of characteristic parameters

4 行驶工况优化模型

4.1 自编码器模型

基于随机选择构建行驶工况的方法易于理解，但是随机性太强，构建工况误差不稳定。为此，研究通过添加约束条件的方式改进自编码器建立优化模型。该模型将输入工况作为学习目标，对输出工况进行表征学习并加以优化，具体结构[11]如图7所示。

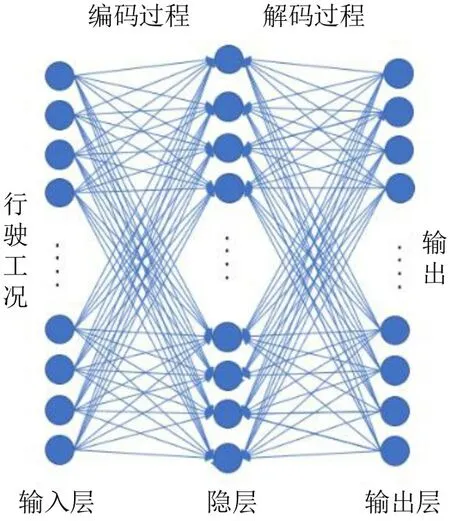
图7 自编码器图示Fig.7 Diagram of autoencoder

为了缩小行驶工况与原始数据特征参数间的相对误差，将行驶工况作为模型的输入，即输入3.4节中构建工况的逐秒速度数据，但其意义并不在于简单的重构行驶工况，而是在重构自身的同时，加入新的损失函数，使输出行驶工况的相对误差更小。如果仅将特征参数误差作为损失函数，会导致输出工况不符合实际。因此将构建工况作为输入，设置两个损失函数：一是输入与输出之间的均方差；二是输出工况与原始数据特征参数间的相对误差。以此保证输出工况缩小误差的同时不脱离车辆实际运行规律。

4.2 参数设置

基于Python3.8 语言和Tensorflow2.0 平台搭建自编码器优化模型，输入与输出的神经元个数均为构建工况的时间长度。为了更好地学习到输入数据的特征、简化计算复杂度，设置单个隐藏层、共1300 个神经元，选取relu 函数作为激活函数，选取SGD优化器，学习率大小为3×10-5，损失函数为

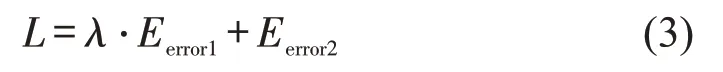
式中：L为损失函数；Eerror1为特征参数相对误差；λ为Eerror1权重；Eerror2为输入与输出间的均方差。

计算Eerror1时包括11个特征参数，λ和各个参数的权重均为可调节的超参数，以优化效果为目标重复多次实验进行调参，最终确定λ值为1.5，平均速度和平均行驶速度的权重均为200，平均加速度和平均减速度的权重均为100，其余参数权重均为1。

4.3 模型优化结果验证

经过150 次迭代，模型收敛。结果显示，由于机器学习利用模型对数据进行拟合，导致输入工况速度为0 km·h-1的时段对应输出结果在0 km·h-1上下很小范围内波动，因此将输出结果小于0.1 km·h-1的值近似取值为0 km·h-1。计算优化结果的特征参数误差，结果显示平均误差由2.97%缩小到2.39%。具体误差如表5所示，加速度标准差误差由6.43%降到5.14%，匀速时间比误差由5.82%降到4.76%，但由于工况1参数平均误差小，其余参数优化效果并不显著。

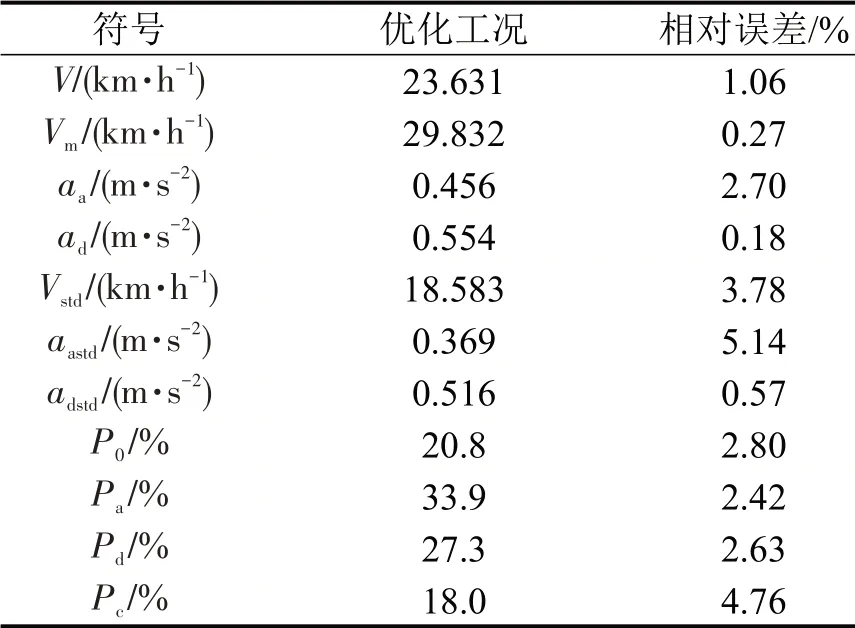
表5 优化工况特征参数分析表Table 5 Characteristic parameter analysis table of optimized driving cycle

为再次验证模型优化效果，在工况集合中随机选取一个工况(简称工况2)输入自编码器进行优化。工况2的时间-速度曲线如图8所示，平均相对误差为4.90%，具体参数取值及优化效用如表6所示。总体优化效果明显，平均优化效用达到1.25%。由此可见，当构建工况特征参数平均相对误差较大时，模型的优化效果更好，说明自编码器可以很好地克服随机选择过程中误差不确定性大的缺点。

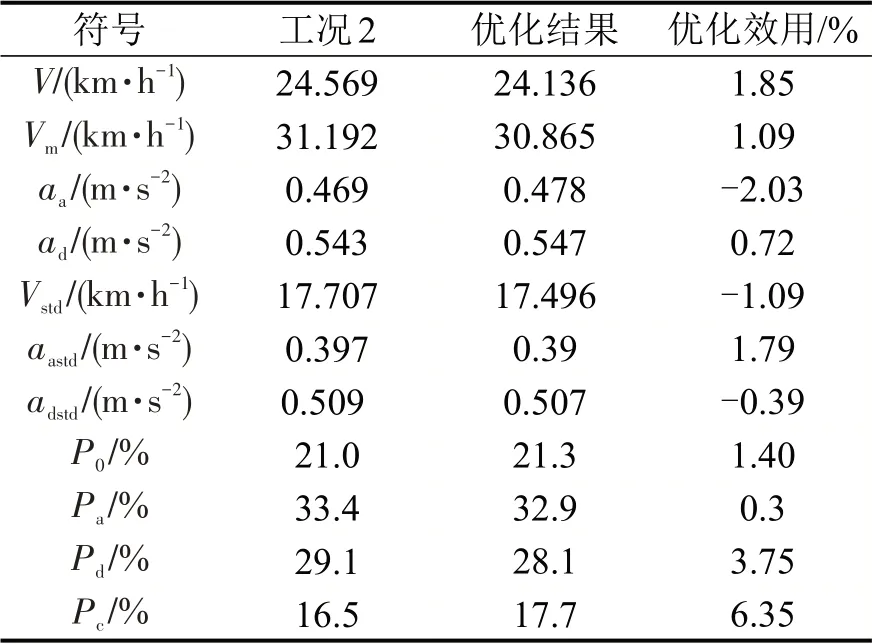
表6 工况2的优化结果Table 6 Optimization result of driving cycle 2

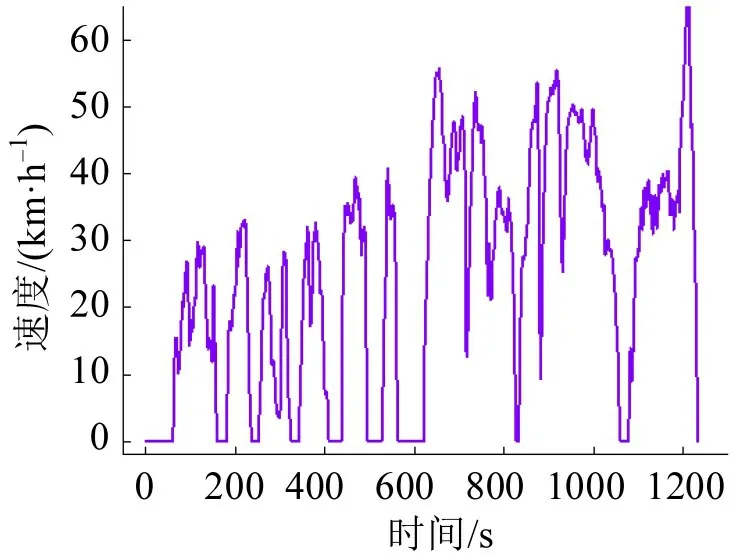
图8 工况2的时间速度曲线Fig.8 Time-speed curve of driving cycle 2

4.4 优化策略分析

为了直观了解模型的优化策略，可视化工况1、工况2优化前后的差值图，如图9和图10所示。由于工况1的平均行驶速度略低，因此模型通过提升车辆行驶状态的运行速度以缩小误差，比较符合实际，证明了优化模型的可行性。

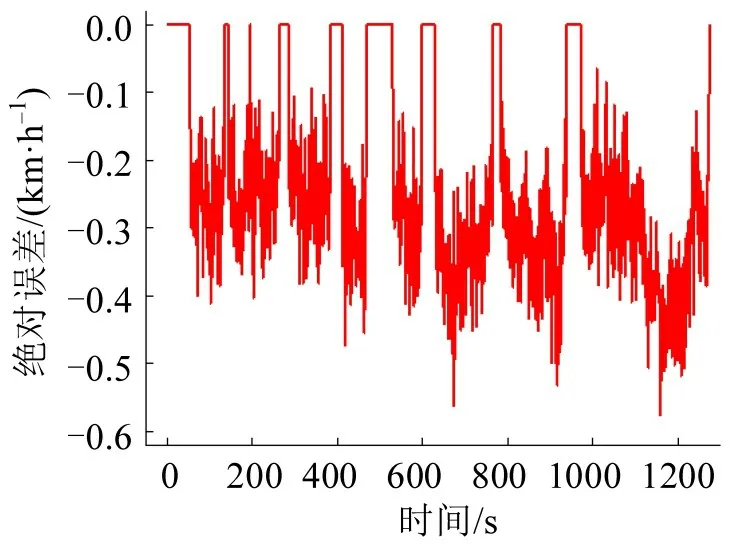
图9 工况1优化前后差值图Fig.9 Difference graph of optimized driving cycle 1 and driving cycle 1

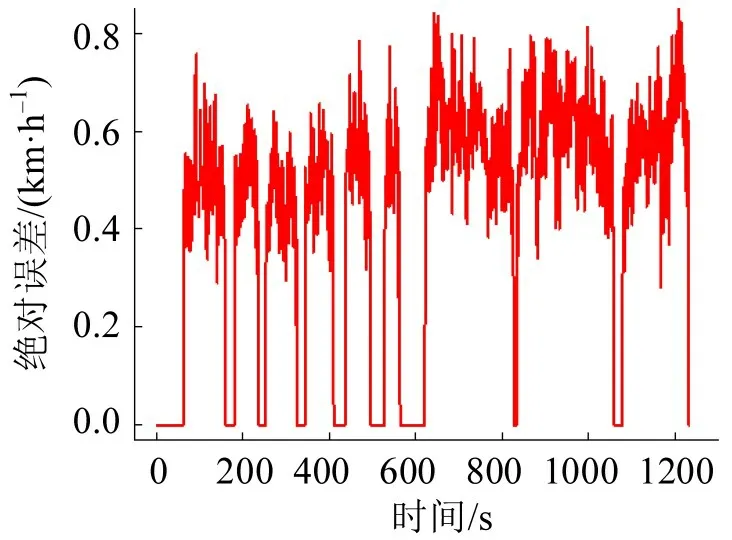
图10 工况2优化前后差值图Fig.10 Difference graph of optimized driving cycle 2 and driving cycle 2

工况2 的平均速度和平均行驶速度均高于原始数据，如图10所示，模型通过降低车辆行驶状态的运行速度以缩小误差。且优化幅度比工况1更大，说明自编码器模型的优化策略更符合实际情况。

5 结论

研究基于仿真数据强化学习的数据分析理论，通过对自编码器的损失函数施加约束，提出混合约束自编码器的工况智能优化算法，构建了采集数据预处理-短行程片段划分-随机选择合成工况-自编码优化的系统性工况的智能方法。重点研究了不脱离车辆实际运行规律，缩小特征参数值与原始数据误差，最终将平均误差由2.97%缩小到2.39%。分析了模型的优化结果以及优化策略，发现对于误差较大的工况，优化效用更高且优化策略符合实际。解决了基于随机组合构建工况过程的误差不稳定、可靠性差的问题。

验证了自编码器优化工况的可行性，并给出具体模型参数取值推荐。不同的驾驶行为和机动车类型会展现出不同的工况特性，而本文获取数据较为单一，同一辆车仅能代表单一驾驶行为、单一机动车类型，因此未来可在加大数据量的条件下综合考虑不同驾驶行为，开展面向不同城市本地化机动车行驶工况的构建，并进行不同机动车类型的工况构建研究，进一步验证所提出方法的可行性。