巧借切线解圆锥曲线顶点定值子弦问题
甘肃省兰州市第六中学 焦永垚 (邮编:730060)
1 顶点定值子弦的含义
设点P是圆锥曲线的一个顶点,PA、PB是该曲线过顶点P的两条弦,当直线PA、PB的斜率的和(或积)为定值λ时,称线段AB为该曲线顶点P的关于λ的斜率等和(或积)子弦[1].
圆锥曲线顶点定值子弦问题在历年全国高考和竞赛中频繁出现,学生解题时往往先将直线方程与圆锥曲线方程联立,消元后利用韦达定理求得两根的关系,再根据已知条件进行转化和计算,过程非常繁杂.现运用“借切线法”解决圆锥曲线顶点定值子弦问题,思路新颖,运算简捷,有利于学生掌握.
2 构建模型,初探方法
例1已知A、B为椭圆C:+y2=1 上的两个动点,点P(0,1),直线PA、PB的斜率分别为k1、k2,且k1k2=求证:直线AB过定点.
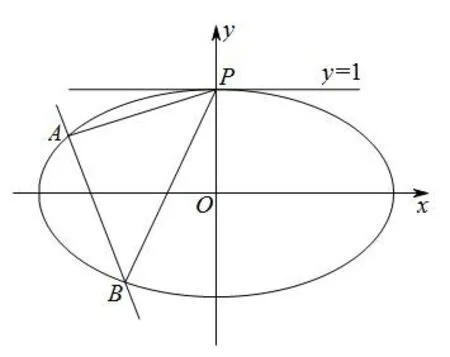
图1
证明直线PA的方程为y=k1x+1,即k1x-y+1=0.同理直线PB的方程为k2xy+1=0,两式相乘得(k1x-y+1)(k2x-y+1)=0,化简整理得
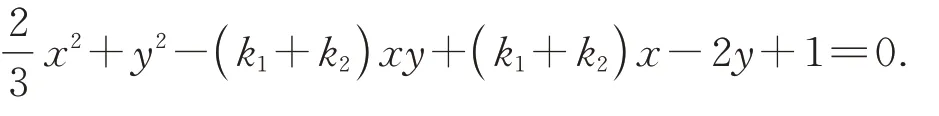
点P、A、B同时满足上式和椭圆的方程,由椭圆方程得x2=3-3y2,代入上式整理得y2+[(k1+k2)x+2]y-(k1+k2)x-3=0,分解因式可得(y-1)[(k1+k2)x+y+3]=0,则y-1=0 或(k1+k2)x+y+3=0,其中y-1=0 为椭圆在点P处的切线方程,则(k1+k2)x+y+3=0为直线AB的方程,恒过定点(0,-3),得证.
3 探究本质
为什么把椭圆方程x2=3-3y2代入方程+y2-(k1+k2)xy+(k1+k2)x-2y+1=0 中,就一定能分解为过顶点的切线方程与直线AB的方程相乘呢?这需要从曲线系方程谈起,关于曲线系,有下面的结论:
⑴若直线l1:A1x+B1y+C1=0 和l2:A2x+B2y+C2=0 与曲线C:f(x,y)=0 有四个不同交点,则过这四个交点的曲线系方程为:λf(x,y)+μ(A1x+B1y+C1)(A2x+B2y+C2)=0(λ、μ∈R).
⑵若四直线li:Ai x+Bi y+Ci=0(i=1,2,3,4)有四个不同交点,则过这四个交点的曲线系方程为:
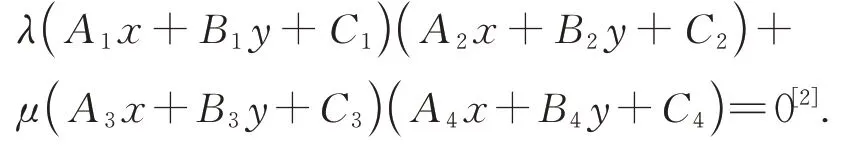
先探究顶点定值子弦问题一般情况(以椭圆及其上顶点为例):
已知A、B为椭圆C:=1(a>b>0)上的两个动点,点P(0,b),直线PA、PB的斜率分 别 为k1、k2,则直线PA、PB的方程为k1xy+b=0 和k2x-y+b=0,由结论可知过点P、A、B的曲线系方程为
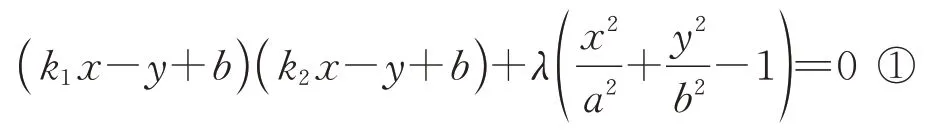
此处点P可看作两个交点蜕化成为一个点,则结论中四条直线中的一条蜕化成为过点P的切线,易知此切线方程为y-b=0;因为过三点P、A、B的曲线系中包含过点P的切线和直线AB,所以将方程y-b=0 代入①式,得=0;因为x≡0,所以得λ=-a2k1k2,再代入①式消去“x2”.这一过程直接从椭圆方程中解出x2,再代入方程(k1x-y+b)(k2x-y+b)=0.这就是例1 解法的理论依据.
由此可见,对于圆锥曲线顶点定值子弦问题,可采用“借切线法”解决,归纳为以下步骤:
⑴根据条件分别设出过顶点的两条直线方程;
⑵把两条直线的一般式方程相乘,并整理;
⑶把整理的方程与圆锥曲线的方程联立,如果顶点在y轴上,则消去x2,如果顶点在x轴上,则消去y2;
⑷把得到的方程整理成关于x(或y)的一元二次方程,再分解因式,得到两条直线方程,其中一条为过顶点的切线方程,另一条为顶点定值子弦所在直线方程,从而可得此直线恒过定点.
4 模型的应用
4.1 顶点斜率等和子弦问题

⑴求C的方程;
⑵设直线l不经过P2点,且与C相交于A、B两点.若直线P2A与直线P2B的斜率的和为-1,证明:l过定点.
易得C的方程为+y2=1.下面来证明第⑵问.
证明设直线P2A的斜率为k,则直线P2A的方程为y=kx+1,即kx-y+1=0,由题知直线P2B的斜率为-(k+1),则直线P2B的方程为y=-(k+1)x+1,即(k+1)x+y-1=0,两式相乘整理得k(k+1)x2-y2-xy+x+2y-1=0.点P2、A、B同时满足上式和椭圆C的方程,由椭圆的方程得x2=4-4y2,代入上式得(2k+1)2y2+xy-x-2y-4k2-4k+1=0,方程可化为(y-1)[(2k+1)2(y+1)+x-2]=0,解得y-1=0 或(2k+1)2(y+1)+x-2=0,其中y-1=0 为椭圆在点P2处的切线方程,(2k+1)2(y+1)+x-2=0为直线AB的方程,易知直线AB过定点(2,-1),即l过定点(2,-1).
点评本题第⑵问常规解法是设直线l的斜截式方程与椭圆的方程联立,还需讨论l的斜率是否存在.另外,把直线P2A与直线P2B的斜率之和用坐标表示,运算过程相当复杂.而利用“借切线法”解决过程明显比较简捷,大大提高了学生的解题效率.
4.2 顶点斜率等积子弦问题
例3(2013 年四川省高中数学预赛第15 题)已知点B(0,1),P、Q为椭圆+y2=1 上异于点B的任意两点,且BP⊥BQ.若点B在线段PQ上的射影为M,求点M的轨迹方程.
解由题意,直线BP、BQ的斜率均存在且不为0,故设直线BP的方程为y=kx+1,即kxy+1=0,则直线BQ的方程为y=-+1,即为x+ky-k=0,两式相乘整理得kx2-ky2+(k2-1)xy-(k2-1)x+2ky-k=0 .点B、P、Q同时满足上式和椭圆的方程,由椭圆的方程得x2=4-4y2,代入上式得5ky2-[(k2-1)x+2k]y+(k2-1)x-3k=0,即 为(y-1)[5ky-(k2-1)x+3k]=0,可得y-1=0 或 5ky-(k2-1)x+3k=0,其中y-1=0 为椭圆在点B处的切线方程,5ky-(k2-1)x+3k=0 为直线PQ的方程,即y=则直线PQ恒过定点
如图2,因为BM⊥PQ,所以点M的轨迹是以线段BN为直径的圆(除去点B),其方程为0,即
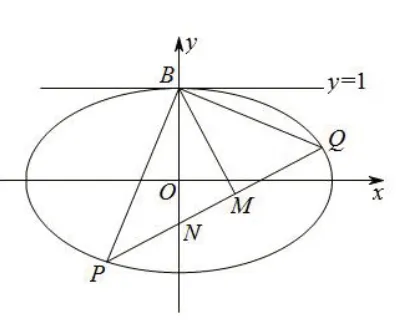
图2
点评本题由条件BP⊥BQ把问题转化成为顶点斜率等积子弦问题,再利用“借切线法”解决,过程与例2 解法类似.
有一类顶点弦问题,虽然表面上不是圆锥曲线顶点定值子弦问题,但也可以将其转化为这类模型解决.请看下面例子:
例4(2020 年全国卷Ⅰ理科第20 题)已知A、B分别为椭E:+y2=1(a>1)的左、右顶点,G为E的上顶点,=8,P为直线x=6 上的点,PA与E的另一个交点为C,PB与E的另一个交点为D.
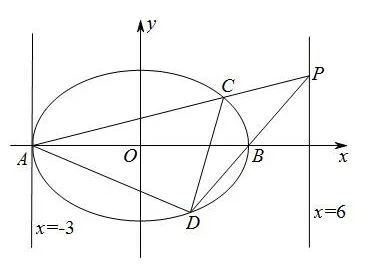
图3
⑴求E的方程;
⑵证明:直线CD过定点.


点评此题虽然表面上看没有明确给出斜率之和(或积)为定值的关系式,但通过计算构造出了一个斜率之积为定值的式子kAC·kAD=-从而把问题转化成了顶点斜率等积子弦问题,再用“借切线法”解决.此类顶点弦问题在历年全国高考和竞赛中多次出现,如2020 年全国高中数学联赛福建赛区预赛第12 题、2020 年全国高中数学联赛江苏赛区市级选拔赛第11 题、2018 年全国高中数学联赛重庆预赛第9 题、2010 年江苏省高考理科第18 题等等,同学们应予以重视.
5 结束语
圆锥曲线顶点定值子弦问题的解法灵活多样,本文介绍的“借切线法”为学生提供了一种新颖的解题视角,丰富了学生的解题思路,开拓了学生的解题视野.在圆锥曲线备考复习中优化解题思路和简化运算过程始终是教师和学生所追求的目标,教师要引导学生在平时解题中多思考,勤动脑,多总结归纳,在数学思想方法的引领下不断提升学生的数学运算核心素养.

