基于迭代法的多目标决策及应用
张甜,阎红灿,2
(1. 华北理工大学 理学院,河北 唐山 063210;2. 河北省数据科学与应用重点实验室,河北 唐山 063000)
决策具有蝴蝶效应,当下所作出的决定会影响到后续的发展,错误的决策会造成难以估计的损失。在决策中,根据决策目标的个数,将决策分为单目标决策和多目标决策。多目标决策是对多个相互矛盾的目标进行科学、合理的选优,并作出最终决策的理论和方法。多目标决策问题存在于社会生活的方方面面,比如选择一个城市去旅游,选择去成都、大理还是上海等,这些景点各有各的特色,最终选择去哪个城市便构成了一个多目标决策问题。常见的解决多目标决策的方法有分层序列法[1]、目标规划法[2]、直接求非劣解法[3]、层次分析法[4]和多属性效用法[5]等。相比于其他方法,迭代法[6]方便简捷,编程易实现。多目标决策方法现已广泛地应用于资源[7-8]、环境[9]、经济[10-11]、管理[12-13]、教育[14]、医疗[15]等领域。
1迭代法
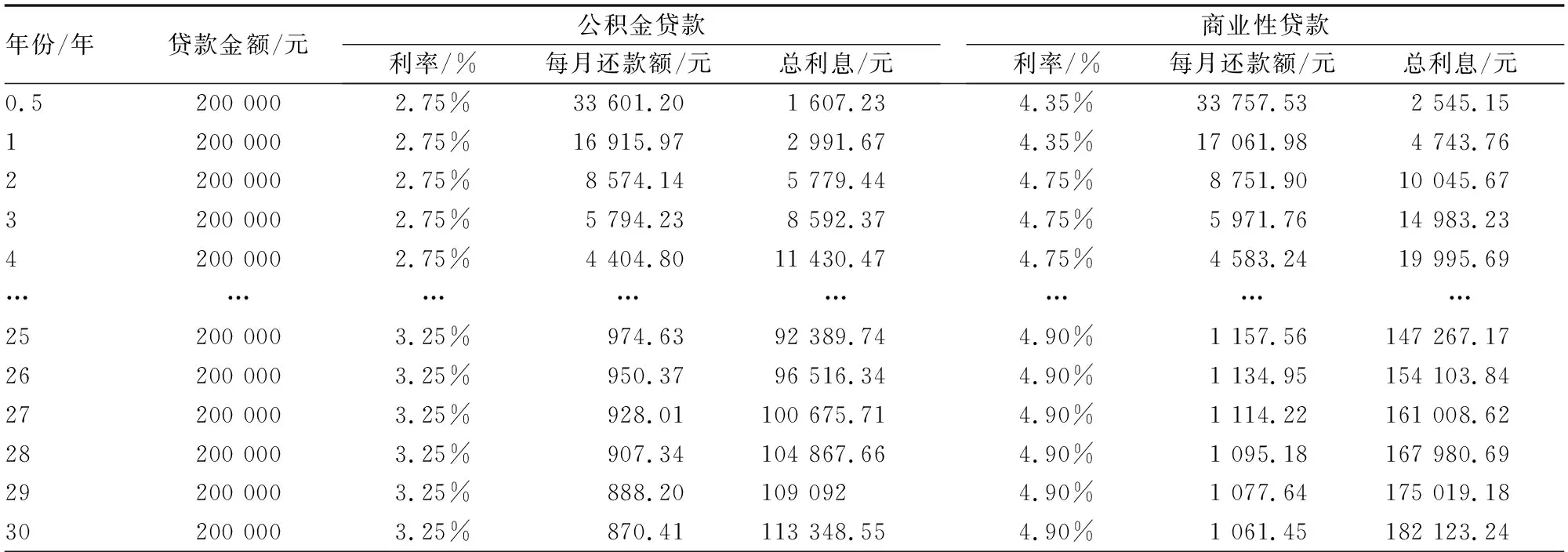
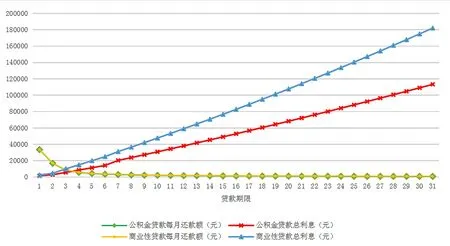
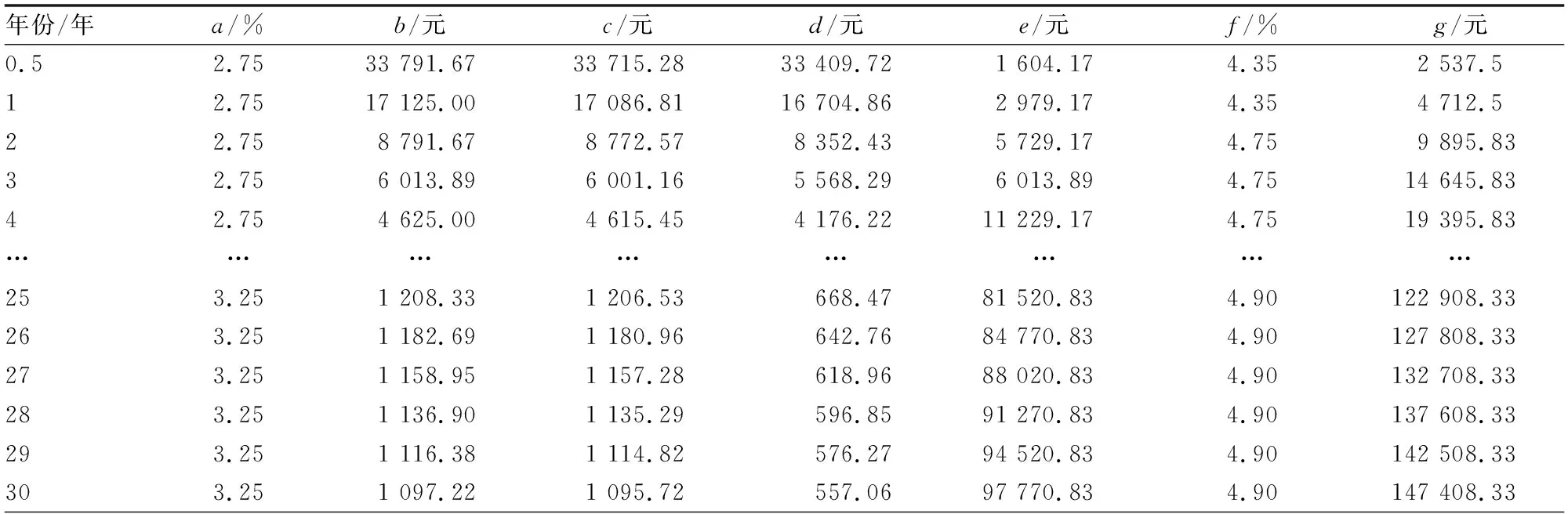
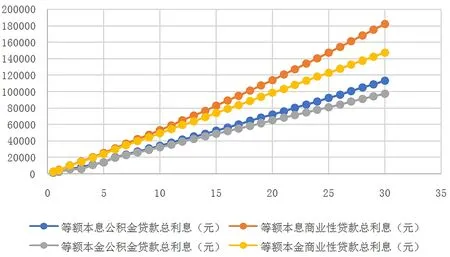
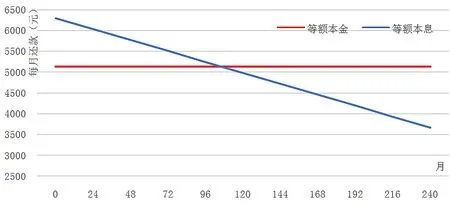
迭代法又称辗转法,是使用可变量之前的值不断类推出新值的过程。当数据量较大且进行相似性计算时,迭代法展现了它独特的优势,可以借助计算机实现快速计算。迭代的算法方式是一种利用类推公式或者循环性算法通过构造序列来求问题近似值的方法。例如,对于非线性方程F(x)=0,利用类推关系式x(k+1)=ψk(F;x(0);x(1);…,x(k)),从x(0)开始按次序计算x(1),…,x(k)来贴近方程的解x*的方法,若x(k+1)只与x(k)有关,即x(k+1)=ψk(F;x(k)),则称此迭代法为单步迭代法;对于线性方程组Ax=b,由关系式x(k+1)=Φk(A,b;x(0);x(1);…,x(k))从x(0)开始依次计算x(1),…,x(k)来贴近方程Ax=b的解的方法。若对某一正整数k0,当k 使用迭代算法的3个步骤如下: Step1:找到算法方式中的可变量,在使用可变量之前的值不断地类推出新的值的过程前,要最少找到一个变量。 Step2:构造出关于变量的相应迭代式,这个迭代式就是使用可变量之前的值不断地类推出新的值的过程。迭代的算法方式中最重要的一步就是构造相应迭代式,一般会按顺序一步步往后推得或者从结果往前推得。 Step3:把握迭代的算法方式的整体进程。有2种情况,一是迭代的次数一定且易算,要预先确定次数的循环;二是迭代的次数不一定,要继续研究如何终止整体进程。 以购房还贷为应用背景建立多目标决策模型。目前,社会上热度最高的贷款方式是等额本息贷款和等额本金贷款,在建立基本还贷模型的基础上,分别建立了等额本息还贷模型和等额本金还贷模型。 在介绍基本还贷模型前,先对所用的符号及基本假设加以说明。符号说明:A0表示需向银行贷款本金;Am表示在第m月还款后仍欠银行的本息;Xm表示第m月的还款额;Rm表示第m月的利息(m=1,2,3……);r表示贷款月利率;R表示还款总利息;T表示总还款期限;r表示贷款月利率。 基本假设:(1)购房者在规定的贷款时间内经济情况正常;(2)银行在贷款期限内月利率不变;(3)每个月的月末贷款人将还款额付给银行;(4)银行使用复利计算的方法来计息。 基本还贷模型可以作为后续对等额本息还贷法和等额本金还贷法建立模型的基础,主要对仍欠银行的本息和作递推,下面介绍基本还贷模型。 第一个月,需向银行贷款本金为A0,利息为R1=rA0,本息和为A0(1+r),还款额为X1,尚欠银行的本息和为A1=(1+r)A0-X1。第二个月,需向银行贷款本金为A1,利息为R2=rA1,本息和为A1(1+r),还款额为X2,尚欠银行的本息和为A2=(1+r)A1-X2。以此类推……第m个月,需向银行贷款本金为Am-1,利息为Rm=rAm-1,本息和为Am-1(1+r),还款额为Xm,尚欠银行的本息和为Am=(1+r)Am-1-Xm。由以上类推,得出基本还贷模型为: (1) 运用迭代法,求出此基本还贷模型的显式解: Am=(1+r)mA0-[(1+r)m-1X1+(1+r)m-2X2+…+(1+r)Xm-1+Xm] (2) 由基本贷款模型可知,若初期的还款额数越大,则本息和递减越快,最后所需的总利息越少。 等额本息还贷法是指每月偿还同等数额的贷款(包括本金和利息),一般称为等额还款。如果每月还款额为X,则X=X1=X2=…=Xm,则还贷模型成为一个常系数线性非齐次差分方程的初值问题: (3) 由基本还贷模型的显式解可推得: Am=(1+r)mA0-X[(1+r)m-1+(1+r)m-2+…+(1+r)+1] (4) 可得到该初值问题的解是: (5) 也可得出每月的利息为: Rm=rAm-1=(A0r-X)(1+r)m-1+X (6) 若该贷款人在T月内还清全部本息,则AT=0。可得: (7) 设银行指定的还款期限为T,则每月固定应还还款额为: (8) 这时可得总利息为: (9) 使用递推法,以此类推……最终得到第m个月需归还银行的还款额为: (10) 所需还款利息总额为: (11) 由此可知,第一月还款的额数最大,随着时间的递增,还款额数将会减少。 运用上述还贷模型做实例分析,直观地认识贷款买房的不同策略,实现多目标决策。李女士准备买一套商品房,其经济条件稳定,基于李女士案例通过对比分析2种还贷模型,决策出最优贷款买房方案。 由于贷款金额主要是由贷款者的实际情况决定,不具备统一讨论的意义,故可将贷款金额固定为200 000元进行数据分析,贷款总利息最少的目标即为最优目标,由此建立目标函数:Z=minR,由实际情况可知,贷款买房最长时限为30年。表1所示为等额本息下公积金贷款和商业性贷款总利息对比。 由表1可知,在等额本息还贷方式的前提下,贷款的总金额一定时,随着贷款年限的增加和贷款方式的不同,贷款基准利率会产生相应的增长,这使得最后需要还付的利息也产生相应的增加,可以看到在还款期限增加的过程中,总利息增长区间较大,但每月还款金额会相对减少。从数据可以分析出,贷款1年时,每月还款额较大,总利息较少;贷款15年时,每月还款额较少,总利息较多;贷款5年时,每月还款额适中,总利息也适中。 表1 等额本息下公积金贷款和商业性贷款总利息对比 图1所示为等额本息还款每月还款额及总利息变化。 由图 1可以看出,在等额本息还贷方式的前提下,从整体趋势来看,商业性贷款下每个月的还贷额数和利息总和数都比公积金贷款下每个月还贷额数和利息总和数要多,公积金贷款的增长趋势相对于商业性贷款要缓慢一些,商业性贷款涨幅较大。此外可以看出,商业性贷款的贷款期限是4年期最为划算,公积金贷款的期限为5年期时最划算。 图1 等额本息还款每月还款额及总利息变化 等额本金还贷法每个月需要还的本金数是相同的,每个月需要还的利息会有所改变,同样以固定贷款金额为200 000元进行数据分析。表2所示等额本金下公积金贷款和商业性贷款总利息对比。 由表 2可知,在等额本金的还贷方式的前提下,每个月需要的还款额数都会减少,且减少的金额在随着贷款期限的增加而增加,成正比。在同一期限下,等额本金还贷方式的月还贷额数会每个月减少同样的金额。商业性贷款的利息总和以及每个月的还贷额数都比公积金贷款的多一些。在贷款期限增加过程中,商业性贷款的总利息多于公积金贷款的总利息。 表2 等额本金下公积金贷款和商业性贷款总利息对比 图2所示为等额本息方式和等额本金方式下总利息的对比。 图2 等额本息方式和等额本金方式下总利息的对比 由图 2可以看出,随着贷款期限的增加,等额本金下的总利息和等额本息下的总利息变化都呈现上升趋势,且商业性贷款无论是在等额本息还款下还是等额本金还款下都比公积金贷款的总利息变化趋势更加陡峭,所以商业性贷款总利息多于公积金贷款总利息。 图3所示为月还贷额比较。 图3 月还贷额比较 由图 3可知,等额本金还贷方式在开始的一个区间内的月还贷额会比等额本息还贷方式的月还贷额高一些,第一个月开始时需要还款6 297.5元,最后一个月需要还款3 677.1元,逐月递减10.96元。但是到第106月时,两者会产生交汇,以后等额本息还款月的还款额将会高于等额本金的月还款额。 等额本金的还贷方式清偿的总利息数较少,贷款时间越久,总利息数额间的差数就越多。初期还贷金额最大,随着还贷月数的递增,后期还贷金额变少,适合年纪偏大或收入状况较乐观的购房者。若购房者收入不够稳定,可以适量延长还款期限,虽然会使需偿还的利息数增大,但在较长时间内,该购房者可以有更多的投资机会,若投资所获得的收益大于需还给银行的利息数,那么也可以选择此种还贷方式。该模型有很多可以深究的地方,比如对贷款的风险估测、选择组合贷款,因此本模型具有很大的改良空间。2基于迭代法的购房还贷模型
2.1 基本还贷模型
2.2 等额本息还贷模型
2.3 等额本金还贷模型
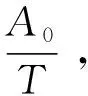
3还贷模型对比
3.1 等额本息时数据对比分析
3.2 等额本金时数据对比分析
4结论

