等额还贷计算方法研讨

丁昌春，吴明官，姬忠光

(黑龙江省水利水电勘测设计研究院，哈尔滨150080)

1 问题的提出

每个社会成员或集体等单位，当一次性贷款(F)后，在银行规定的还贷期限(m=n×t)内，按指定的计息周期(1/t=日、月、季、年等)、利率(i=r/t)，等额还款的情况下，如何计算还贷本息，直接影响到各单位和个人的切身利益。即在一次性贷款后，具体的还款方式对还贷者具有较大的影响，如:等额本息(A)还款、等额本金(F/m)还款、单利法、复利法、时段末结算、时段中结算等。

在水利工程经济评价中，为了弄清不同还款方式对还贷者带来的具体影响，详细推导了单利法、复利法还贷计算公式及相互关系等，目的是方便广大还款者事先主动了解和掌握不同贷款前提条件及各种方法之间的差别等有关内容。

1.1 等额本息还款

根据等额本息还款方法，分析逐年的本利和Ek表达式如下:

1.2 等额本金还贷

根据等额本金还款方法，分析逐时段还贷利息Sk表达式如下:

2 单利法还贷利息计算公式

从上述等额本金还贷利息Sk表达式中可以看出，当不考虑复利(利息再取利息)的情况下，单利法等额本金还贷利息总额计算公式推导过程如下:

公式(2)就是单利法等额本金还贷利息总额计算公式，该法的计算公式比较简单易用，故直接采用即可。

3 复利法还贷计算公式

3.1 等额本息还款额计算

3.1.1 时段末结算

从上述等额本息还款Ek表达式中可以看出，当考虑时段末结算的情况下，复利法等额本息还款额(A)计算公式推导过程如下:

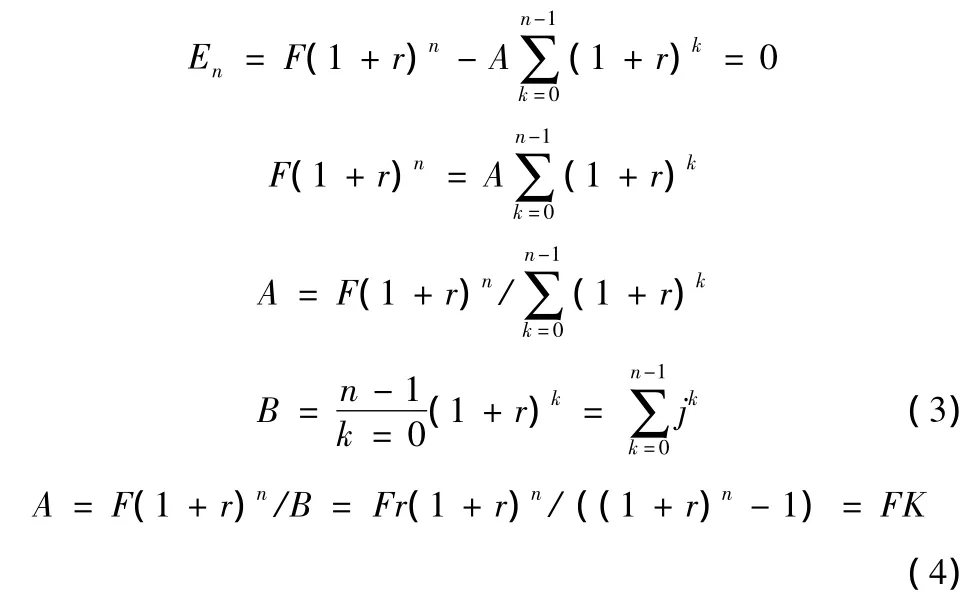
式(4)就是目前我国银行系统给购房者放贷中，最常用的年等额本息还款额(A)的计算公式。

由式(4)求得年等额本息还款额A的基础上，计算本利和E、不同计息周期(1/t=日、月、季、年等)相应的平均还款额P。

方法1:平均法

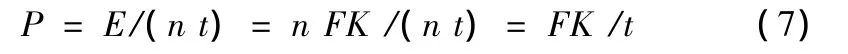
式(7)就是在先求得时段长为年的还贷本息情况下，还贷期内平均等额本息还款的计算方法，简称:平均法。

方法2:直接法

式(8)就是在一年计息t次的情况下，目前银行系统常用的等额本息还款的计算方法，简称:直接法。

3.1.2 时段中结算

从上述等额本息还款的本利和Ek表达式中可以看出，当考虑时段中结算的情况下，复利法等额本息还款额(A°)计算公式推导过程如下:

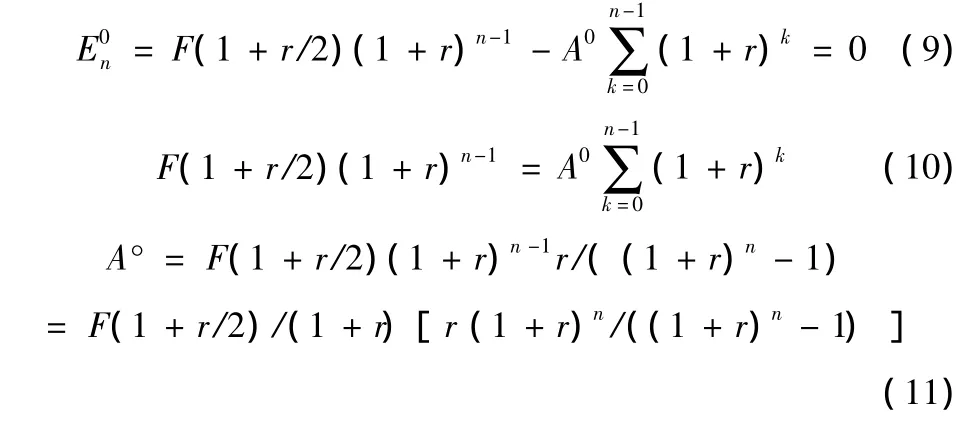
由式(5)代入式(11)得:

式(12)就是时段中结算的等额本息还款额(A°)的计算公式。

3.1.3 等额本息还款时机成果比较

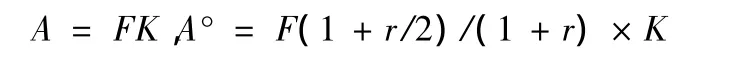
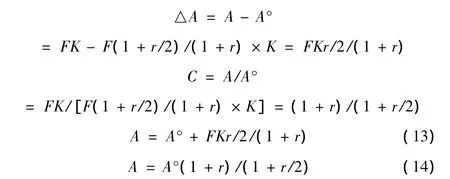
因此，式(13)和式(14)就是时段中结算的年等额本息还款额(A°)和时段末结算的年等额本息还款额(A)关系式。

因为，(1+r)/(1+r/2)＞1，所以，年等额本息还款额计算成果，时段末(A)大于时段中(A°)成果。

3.2 等额本金还贷计算

从上述等额本金还贷利息Sk表达式中可以看出，当考虑复利(利息再取利息)的情况下，还贷利息总额计算较复杂，具体的推导过程如下:

由式(4)代入式(15)得:

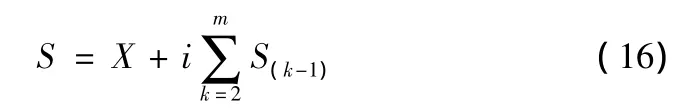
因为，

所以，

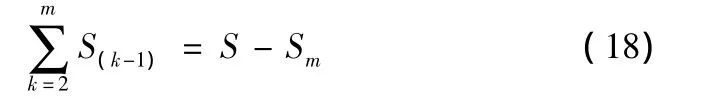
由式(18)代入式(17)得:

式中:Sm=(F－(m－1)/mF)i+Sm－1i=F(1－(m－1)/m)i+Sm－1i

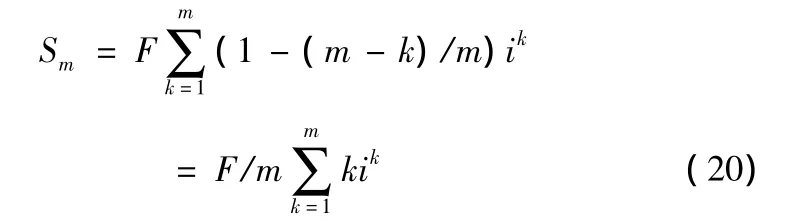
式(20)和式(4)代入式(19)得:

公式(21)就是等额本金复利法还贷利息总额计算公式。

由式(21)求得等额本金还贷利息总额S的基础上，计算本利和E、不同计息周期(1/t=日、月、季、年等)相应的平均还款额P。

3.3 等额本金还贷复利法近似公式

由于复利法等额本金还贷利息总额计算公式较复杂，故通过分析复利法和单利法的关系，推导出复利法简化后的近似公式。

复利法S≈A单利法≈AX

又从式(24)可以看出，若还贷计息周期取月(m=年数n×12)、日(m=年数n×365)时，m值很大，即2i/m/(m+ 1)/(1－i)2≈0，则复利法简化后的近似公式如下:

式(24)和式(25)就是时段末结算的复利法等额本金还贷利息总额简化的近似公式。

当i=r/t，m=nt时，由式(25)得:

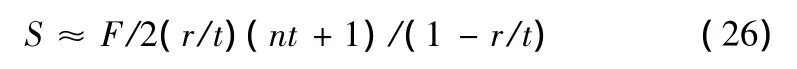
当t→∞时，对式(26)求极限后得:

式(27)就是计息周期(1/t)趋近于零时，时段末结算的复利法等额本金还贷利息总额计算公式。

4 分析与讨论

4.1 计息周期

若计息周期为(1/t)(即1 a计息t次)，则E=F(1+r)n就要修改为:

4.2 等额本金还款

一次性贷款后，等额本金还款的时机，对还贷利息总额也有一定的差别，即规定时段内，可以取时段末、时段中。

4.2.1 单利法

从上述等额本金还贷利息Sk表达式中可以看出，当不考虑复利(利息再取利息)的情况下，时段中结算的单利法等额本金还贷利息总额计算公式推导过程如下:

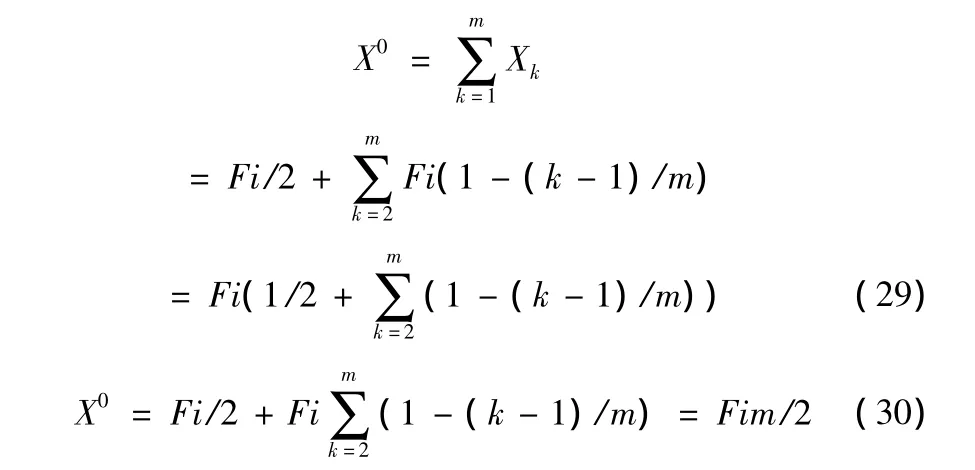
4.2.2 复利法

同样可以推求时段中结算的复利法等额本金还贷利息总额计算公式如下:

S°≈(1－2i/m/(m+1)/(1－i)2)/(1－i)X°(31)

4.2.3 等额本金还款时机成果比较

公式(30)就是计息周期内时段中结算的单利法等额本金还贷利息总额计算公式(X°=Fim/2)，与时段末结算的单利法等额本金还贷利息总额计算公式(X=Fi(m+ 1)/2)，比较(X－X°=Fi(m+1)/2－Fim/2=Fi/2)或( X/X°=Fi(m+1)/2/Fim/2=1+1/m)结果，时段末结算的单利法等额本金还贷利息总额X比时段中结算的单利法等额本金还贷利息总额X°多Fi/2或比值为1+1/m，也就是差第一时段后半个时段的利息。公式(31)的分析结论(S/S° =Fi(m+1)/2/Fim/2=1+1/m)与公式(30)分析结果相同。

4.3 等额本息还款与等额本金还款的差别

一次性贷款额F=40万元，在银行规定的还贷期限(n =20年)内，按指定的计息周期(1/t=1/12=月)、年利率(r =4.9%)，采用复利法等额还款、时段末结算的情况下，等额本息(A)还款和等额本金(F/m)还款的具体差别分析如下:

4.3.1 等额本息(A)还款

平均法:P=E/(n t)=63.650894万元/(20×12)= 0.2652万元/月。

直接法:P1=F(r/t)(1+r/t)nt/((1+r/t)nt－1)=40万元×6.54444×10－3=0.26178万元/月。

4.3.2 等额本金(F/m)还款

4.3.3 差别分析

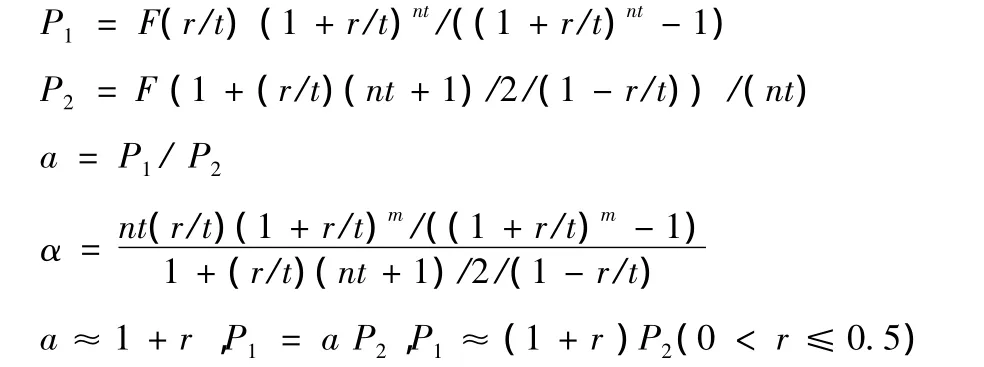
因此，同样采用复利法等额还款，但由于采用的等额不同，等额本息(A)还款和等额本金(F/m)还款的具体差别较大，从上述的例子可以看出，等额本息(A)还款与等额本金(F/m)还款的本利和E、每月的还款额P，分别差3.0672万元、127.8元/月;相对差为5.13%，a=P1/P2=1.0513≈1 +r=1.049。

4.4 分析结论

由于等额还款时机，取时段末和时段中的还贷利息总额，时段末的大于时段中的成果;无论是取时段末或时段中的还贷利息总额，单利法小于复利法;等额本息还款和等额本金还款时，采用平均法还贷本息大于直接法计算成果，而且等额本息还款额大于等额本金还款额。因此，真正落实贷款时，还贷者角度看，尽量争取时段中结算、单利法、直接法和等额本金还款的成果，更有利于还款者。

从计息周期分析成果中可以看出，存款者角度看，在确定存款额和年利率、存款年限、一次性还本付息的条件下，计息周期越小，本利和越大，越有利于存款者。

另外，从等额本息(A)还款与等额本金(F/m)还款的本利和E、每月的还款额P的差别分析成果中可以看出，目前我国银行系统给购房者放贷时，为什么采用等额本息(A)还款方式，很显然，在相同的贷款条件下，等额本息(A)还款比等额本金(F/m)还款方法，更有利于银行。

5 算例

一次性贷款总额F=100万元，银行规定的还贷年限n =20 a，指定的年利率r=7.05%。分别计算规定时段取年、半年、季度、月、旬、日的等额还贷情况下的利息总额和平均每时段的还款额。具体成果详见表1和表2即可。

以20 a还贷期限的100万元，采用直接法放贷计算，按照每月均等的还款方式，年利率为7.05%时，月均还款额P，等额本金还款为7134元/月、等额本息还款为7 783元/月，相差649元/月;本利和E，等额本金还款为171.2122万元、等额本息还款为186.792万元，相差15.5798万元，相对差为9.1%。

从表2中可以看出，复利法的普通公式和简化公式，当规定的时段缩小到月时，还贷利息总额非常接近;当规定时段缩小到日时，复利法和单利法的还贷利息总额也很接近，相对差约0.2‰;当规定时段继续缩小到零时，复利法和单利法的还贷利息总额均等于S=X=nFr/2。

［1］吴恒安.财务评价、国民经济评价、社会评价、后评价理论与方法［M］.北京:中国水利水电出版社，1998.

表1 不同计息周期等额还款额计算成果比较表 万元/t

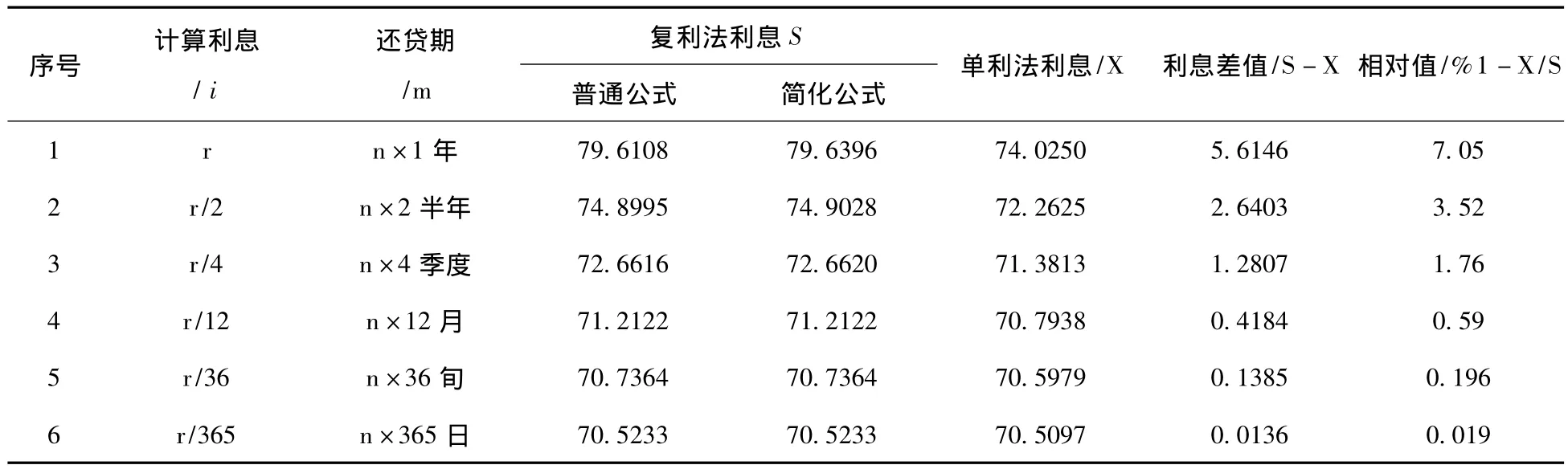
表2 等额本金还贷利息总额计算成果对比表 万元