基于BP神经网络的Q235钢力学性能预测模型

刘志伟，马劲红，陈伟，王文正

(1. 华北理工大学 冶金与能源学院，河北 唐山 063210；2. 现代冶金技术教育部重点实验室，河北 唐山 063210)

引言

Q235钢的生产需要经过熔炼、热处理、轧制等复杂的过程，力学性能往往难以优化。传统的力学性能优化方法是通过结合理论与经验探究轧制、成型等过程中复杂的物理机制，设计优化材料的力学性能。目前对于金属材料力学性能的预测方法可分为3种[1]：第一种是在实验设计和生产过程中整理出来的经验模型。此类模型往往精度不高，且只对单一产品有效，泛化能力较差。第二种是变形机制、成型理论等基础上开发的物理模型。此种模型偏理论化，实际中差异往往较大，需要理想化假设，导致适用范围过窄。第三种方法是神经网络智能学习算法。神经网络具有良好的收敛复杂非线性系统的特点，可自发组织、学习及处理[2,3]。

目前，曾有很多学者对神经网络模型进行改进。Govindhasamya等[4]探讨了隐含层层数和激活函数类型对BP网络性能的影响。Shubhabrata等[5,6]将BP神经网络、模糊逻辑推理与遗传算法结合，通过优化BP学习算法的网络结构，建立预测能力更强的神经网络模型，提高了模型对H型钢力学性能的预测精度[7]。

利用BP神经网络自身的结构特点，研究了BP网络结构设计中的重要因素—隐藏层节点数的选取方案。隐含层数确定后，隐含层上的神经元会影响性能。如果神经元数量过少，网络难以达到预期训练结果，就会产生较大误差。如果隐含层的神经元太多，虽然网络可以很好地学习并达到预期的精度，但它会产生过拟合并降低 BP 神经网络的泛化能力[8]。因此，已经确定隐含层的神经元数量后，目标是让网络不仅能够达到预期的效果，在增大误差精度同时也具有较高的泛化性。基于某钢铁公司Q235钢生产数据建立BP神经网络预测模型，提出BP网络隐含层节点数的选取方法。讨论隐含层节点数与模型之间的规律，从训练步数和预测精度2个角度分析了最优的隐含层节点数选取过程，并利用实际生产数据进行验证和泛化能力测试。

1 BP网络原理

与生物学习类似，利用BP网络预测时，同样存在训练过程，使模型经训练后具备预测能力。神经网络类似于具有生物神经元的节点或神经元的网络。节点与加权相互连接且可调节，因此神经网络具有良好的非线性映射能力。利用某钢铁实际生产数据集进行网络训练，拟合出此种加工工艺下合金元素和力学性能之间的关系。

BP网络训练过程一般分为前馈和反馈2个过程。输入层m个变量后，前馈到隐含层和输出层。输入层与隐含层、隐含层与输出层均由权值和阈值连接。xi(i=1,2…,m)表示任一输入量，隐含层有s个神经元，yi(j=1,2…,s)表示隐含层的输出量。则神经网络正向传播过程可表示为[10-15]：

(1)

(2)

式中：激活函数为f；ω和v表示权值；γ和θ表示阈值；zk表示网络的输出量；输出层有n个神经元。式(1)和式(2)完成了xi(i=1,2…,m)到zk(k=1,2…,n)的映射，则误差可表示为式(3)：

(3)

式中：Mk(k=1,2…,n)表示输出目标值；δ为误差。将公式(3)作为目标函数，误差反馈传播使目标函数最小化。利用误差对隐含层和输出层之间的权重进行反馈调整分别为：

(4)

(5)

式中：η为学习率；v'和θ'为调整后的权重。对于输入层和输出层之前权重ω和γ，同理可调整为ω'和阈值γ'：

(6)

(7)

2 BP网络预测分析

2.1 隐含层节点数的确定

用于训练BP网络模型的数据库来自某钢铁公司100组实际生产的Q235钢连续数据如表1所示，其中包括合金成分(C、Si、Mn、P、S、V、Nb、Ti、Cr、Ni、Cu、Sn、Mo、B)、碳当量(CE)、屈服强度(YS)、抗拉强度(UTS)、延伸率(EL)。将100组数据分为3组：其中70组作为训练集，15组作为测试集，15组作为泛化能力验证集。

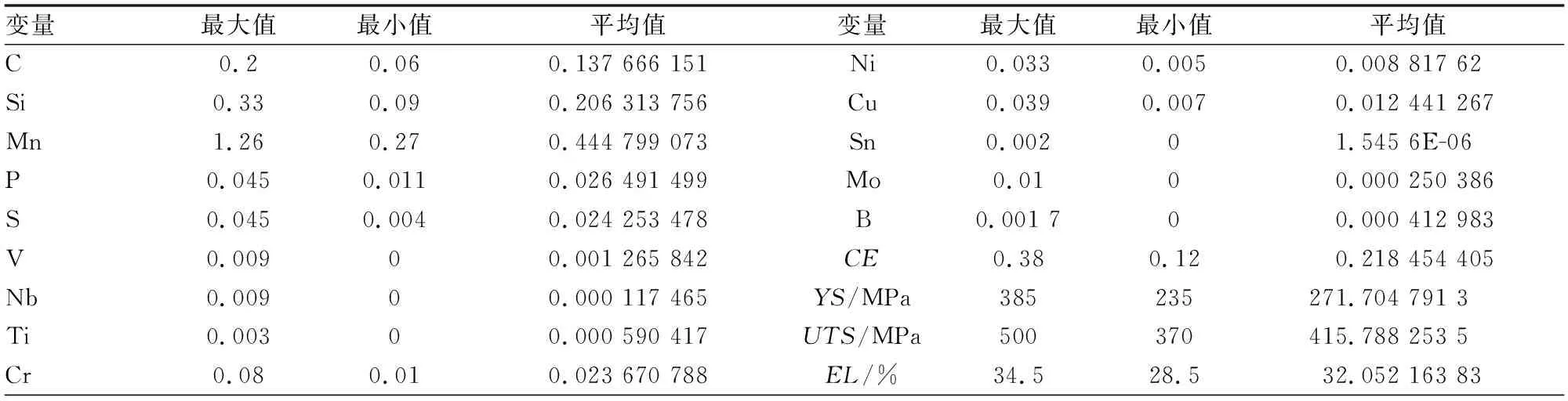
表1 某钢铁公司实际Q235生产数据

依据BP网络的基本原理，建立一个输入层、隐含层和输出层构成的3层BP网络预测模型。依照表1，输入变量为合金元素种类(C、Si、Mn、P、S、V、Nb、Ti、Cr、Ni、Cu、Sn、Mo、B)和碳当量，输出变量为3种力学性能指标(屈服强度(YS)、抗拉强度(UTS)、延伸率(EL)，因此将BP网络输入层和输出层节点数分别确定为15和3，隐含层和输出层的激活函数默认为型函数(Tansig)和线性传递函数(Purelin)。以往的隐含层节点数确定方法：第一种是根据经验确定节点数(Empirical method)，如输入神经元个数与输出神经元个数之和的一半，即(m+n)/2；第二种为修剪法(Pruning method)，初始建立足够多的节点数，在训练过程中，根据节点数的相关程度，删除重复的节点，此方案工作量巨大，该研究不采取此方法。因神经网络的训练精度不仅与网络结构相关，同时与输入的样本数量息息相关，因此提出利用样本数量和修正系数对第一种经验方法进行修正，即公式(8)：

(8)

式中：α为修正系数取0.1～0.5；Q为训练集样本数70个；m为输出神经元个数；n为输出神经元个数。

从BP网络自身特点及预测效果两方面出发，且由样本的平均绝对百分比误差(MAPE)来表示模型训练的精度，采用如下公式：

(9)

式(9)中，Q为测试集样本数420个；Xtest为测试集样本；Xsim为输出结果。当MAPE值越小时，说明模型精度越高；当训练步数越小，说明模型训练效率越高。训练总次数即为网络收敛到设定误差时运行的总步数(Epochs)；相同训练次数下测试样本的均方误差值反映了测试集样本预测值与目标值的偏差。2个指标反映了神经网络模型的性能，训练总次数小，说明模型运行的时间越短、效率高；相同训练次数下测试样本的均方误差值小，说明模型的预测精度高。由此可制定如表2所示的实验对比方案：

表2 隐含层节点数的选取

图1所示为修正系数的确定过程。根据测定，测试集输出力学性能均在α为0.2时，MAPE值最低，模型精度最高，对应的隐含层节点数为12。根据图1可知，模型的训练步数随着α增大，呈现先下降再升高的趋势。当α为0.2、隐含层节点数为12时，模型的训练步数最少，训练速度最快，训练步数为110步。

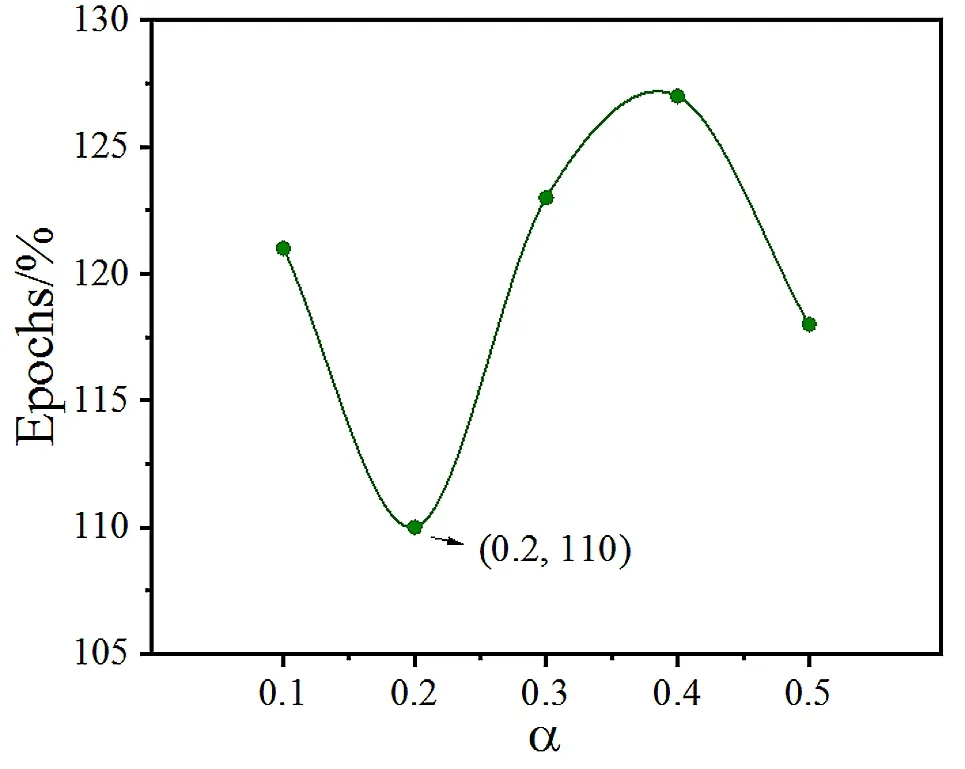
图1 训练步数与α的关系

2.2 泛化能力测试

泛化能力是指机器学习算法对新样本的适应能力，适应隐含在数据背后的规律，对具有同一规律的学习集以外的数据，经过训练的网络也能给出合适的输出，该能力称为泛化能力。

通常情况下，通过测试MAPE值来评价机器学习方法的泛化能力。并非训练的次数越多越能得到正确的输入输出映射关系，网络的性能还需用其泛化能力来衡量。利用剩余的15组数据进行泛化能力测试，如图2所示。

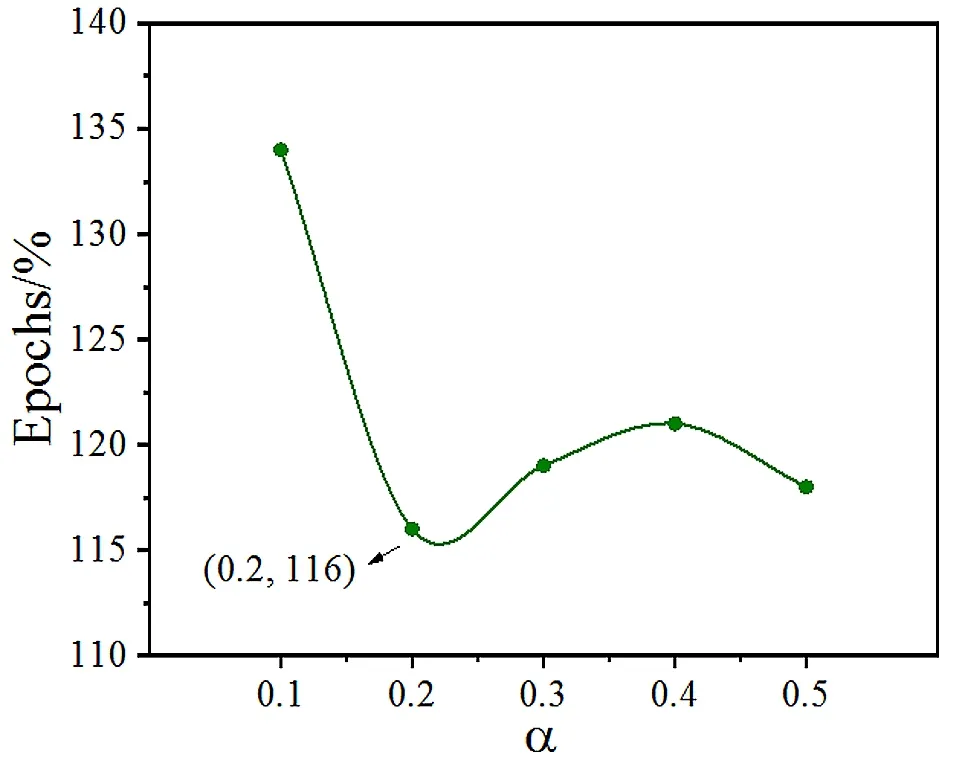
图2 泛化能力测试过程中训练步数与α的关系

根据测定，当α为0.2时，MAPE值分别为6.5%、15.1%、11.2%，模型针对抗拉强度、屈服强度、延伸率3个指标的预测精度仍然较高，达到最佳效果，且训练步数最少为116。表明该模型对同一来源的新数据也具有一定的准确性和适用性。隐含层节点数的选取过程中，利用α因子作为指导可相对更快速地找到最优值。

3变形抗力的预测

北京科技大学管克智、周纪华[16]利用高速变形凸轮试验机对多种钢材进行了高温、高速变形抗力试验，建立了常用的热轧变形抗力结构模型，如公式(10)所示。为了使变形抗力模型适应计算机控制的要求，对钢种数据进行非线性回归分析，得到如表3所示Q235钢的回归系数。

表3 Q235钢变形抗力模型回归系数

(10)

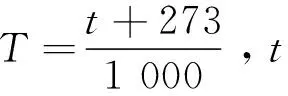
计算变形抗力，先在Excel表格中输入参数变量数值，然后运行MATLAB程序语言。最后系统自动计算出相应的变形抗力结果，保存到指定位置。

部分代码如下：

%% 变形抗力计算

%% 基本参数设定

H=xlsread('data.xlsx', 1, 'A2:A10000');

% sigma

x=x0.*exp(b1.*T+b2).*power((rp/10),(b.*T+b4)).*b6.*power((r/0.4),b5)-(b6-1).*r/0.4;

%% 写入excel

%% 输出结果

xlswrite('data.xlsx',x,1,s);

4结论

(1)在BP网络模型中，隐含层节点数的选择会对预测结果产生重要影响。从模型的效率和精度角度考虑，输出3个力学性能指标均在α为0.2时，MAPE值最低，模型精度最高，对应的隐含层节点数为12。BP网络的效率最高，精度最高，模型的训练步数也最少，训练速度最快，训练步数为110步。

(2)通过泛化能力测试进一步验证了此隐含层节点数下的BP网络预测能力极佳。其中，抗拉强度、屈服强度、延伸率3个指标的预测精度仍然较高，当α为0.2时，MAPE值分别为6.5%、15.1%、11.2%，达到最佳效果，且训练步数最少为116步。

(3)利用数学模型，MATLAB程序对Q235钢的变形抗力进行了预测，为生产实践提供新的方法。