外推法近似计算区域上柯西主值积分
李金,张晓蕾,桑瑜,张宇鑫
(华北理工大学 理学院,河北 唐山 063210)
引言
柯西主值积分是边界元法中的重要研究内容,被广泛地应用于数学物理、电磁力学、流体力学、断裂力学、化学等领域[1,2]。考虑如下形式的柯西主值积分:
(1)
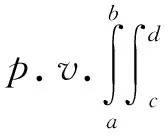
奇异积分的近似计算作为数值计算领域的研究热点。目前,已经有矩形求积公式[3,4]、梯形求积公式[5,6]、辛普森求积公式[7]、高斯求积公式[8]等方法来近似计算奇异积分。LI用矩形求积公式近似计算了二维奇异积分[9],得到收敛结果为O(h2)。文献[10]中讨论了计算柯西主值积分的复合矩形求积公式,逼近密度函数得到误差展开式,设计外推算法提高收敛阶获得后验误差估计。随后有学者研究了多维柯西主值积分的复合矩形求积公式[11],并给出外推算法。矩形求积公式还可以用来近似计算Hadamard有限部分积分[12]。LI等学者利用复合梯形公式近似计算一维、二维及圆上的柯西主值积分[13-15],得到相应的超收敛误差估计。Monegato给出了近似计算二维柯西主值积分的一类插值求积公式[16]。Kim构造了一个基于三角变换的求积公式[17]来近似计算柯西主值积分。
外推法作为一种提高计算精度的方法,近年来被广泛应用于数值计算[18]。在近似计算奇异积分时,根据得到的误差展开式设计外推算法,从而提高误差收敛阶。在等距节点的情况下,通常采用把区间逐次对分的方法计算积分值,这样,前一次划分得到的函数值在区间重新划分后仍可被利用,且易于编程,这是外推法实现的前提。基于以上思路,Navot[19]构造了基于Fourier级数展开的弱奇异积分的Euler-Maclaurin展开式。Lyness研究了二维柯西主值积分的Euler-Maclaurin展开方法[20]。余德浩等学者根据梯形求积公式近似计算二阶超奇异积分得到误差渐近展开式,构造广义的外推算法来提高计算精度[21]。
该研究对复合矩形求积公式近似计算二维柯西主值积分进行分析。对积分区域进行均匀剖分,逼近密度函数与核函数,通过矩形公式近似计算得到误差展开式。构造序列来逼近奇异点,并对网格进行均匀加密,提出了一种外推算法。通过该方法获得更高的收敛阶和后验误差估计。该项研究的第一部分给出了矩形求积公式的基本定义及其近似计算二维柯西主值积分获得误差展开式的相关定理;第二部分证明主要定理,并根据误差展开式得到收敛阶;第三部分在计算二维柯西主值积分误差展开式的基础上,设计外推算法提高收敛阶,并给出后验误差估计;第四部分用数值算例来验证理论分析的正确性。
1主要定理
令a=x0 定理1[22]f(x,y)∈C∞[a,b]×[c,d],θ1,θ2∈[0,1]。定义 (2) 和 (3) 然后有 (4) 其中ck是与h无关的常数。 接下来定义fc(x,y)为f(x,y)的常数插值 fc(x,y)=f(xi-1,yj-1),(x,y)∈[xi-1,xi]×[yj-1,yj],i,j=1,2,…,n (5) 定义线性变换 (6) (7) (8) 其中ωij定义为科特斯系数, (9) 定义φ0(x,y),φk1(x,y),φk2(x,y), (10) (11) (12) 当k=1时, (13) (14) 现在给出如下定理。 定理2设f(x,y)∈C∞(Ω)=C∞[a,b]×[c,d],矩形求积公式In(f,t,s)定义为式(8),存在一个与h无关的常数ck,使得 (15) 其中(t,s)∈(xg-1,xg)×(yl-1,yl), (16) (17) (18) (19) (20) 当k=1时, (21) (22) 当式(18)为0时出现超收敛现象,收敛阶为O(h)。 (23) (24) (25) 证明:根据二维柯西主值积分的定义和线性变换式(6)和式(7),有 (26) 对于式(24)的第一部分 (27) 相似的可以得到式(25)。i≠g,j≠l的情况,相应的黎曼积分可以被同样证明。当k=1时有, (28) (29) 以上可以被类似证明。 引理2在定理2的假设下,有 (30) 证明:通过将fc(x,y),f(x,y)在奇点(t,s)处泰勒展开,得到 (31) (32) 结合式(31)和式(32),得到引理2结论。定理2的证明如下 证明:根据引理2,有 (33) 对于i=g,j=l,有 (34) 结合式(33)和式(34)可得 (35) 这里d0(φ0),dk1(φk1),dk2(φk2)定义为式(18)~式(20)。通过线性变换[xi-1,xi]×[yj-1,yj]映射到[-1,1]×[-1,1],当τ=ξ=0时,d0(φ0)=0。对于最后一部分没有奇异性, (36) (37) 证明完毕。 实际上获得了矩形公式计算二维柯西主值积分的误差展开式,因此当d0(φ0)=0时,得到超收敛点。接下来将以上结论推广到多维的情况。 (38) 这里(t1,t2,...,tq)是奇点,令f(t1,...,tq)∈C∞[ai,bi]q,ai=xi0 fc(x1,x2,...,xq)=f(x1,i1-1,x2,i2-1,...,xq,iq-1) (39) 然后得到: (40) 其中科特斯系数为ωi1,i2,...,iq=hq/[(x1,i1-1-t1)...(xq,iq-1-tq)]。 根据定理2得到矩形公式计算二维柯西主值积分的误差展开式 (41) 并给出如下外推算法,存在正整数n10,n20使得m10:=n10(t-a)/(b-a),m20:=n20(s-c)/(d-c)为常数。为了简化计算过程,设n10=n20,将[a,b]×[c,d]划分为等子区域,得到大小为h1=(b-a)/n10=(d-c)/n20的初始网格Π1,细化网格Π1得到Π2,其大小为h2=h1/2。通过不断细化网格得到{Πj}j=1,2,...,这里Πj由Πj-1得到,网格大小为hj,得到如下所示的外推表。 表1 外推表Ti(j) 对于给定的τ,ξ,定义 (42) (43) T(hi)=T(hi,hj)=I2i-1n10,2j-1n20(f,ti,sj) (44) 下面介绍外推算法步骤 第一步: 第二步: 定理3在定理2的误差展开式基础上,对于τ,ξ=0,根据式(42)和(43)有 (45) 后验误差估计为 (46) 证明:对于给定的τ,ξ,通过式(41)的误差展开式有 (47) 根据柯西主值积分的定义和式(41),将I(f,ti,sj)在奇点(t,s)处进行泰勒展开,有 (48) f(ti,sj)在奇点(t,s)处进行泰勒展开得到 (49) 结合式(47)~式(49)得到 (50) 这里 (51) 对于给定的τ,ξ和bk(t,s,τ,ξ)均为常数,由式(50)有 (52) 根据式(50)和式(52)以及hi=2hi+1,可得 (53) 即 (54) 这里 (55) 继续外推过程可以得到收敛阶O(h3),相似的得到收敛阶O(h4)。通过这种方法,可以得到更高的收敛阶。 这一部分给出一些数值例子验证定理的结论。 例1: 由表2可得,当奇点局部坐标为零时收敛阶为O(h),当局部坐标不为零时则不收敛。因此当τ=ξ=0时,出现超收敛现象并验证了理论分析的正确性。 表2 矩形公式误差估计 例2: 表3 矩形公式外推误差估计 表4 后验误差估计 例3: 表5 矩形公式外推误差估计 表6 后验误差估计 例4: 表7和表8验证了当τ=ξ=η=0时,得到矩形公式近似计算三维柯西主值积分并进行外推的误差,收敛阶可以达到O(h),O(h2),O(h3),O(h4),后验估计的收敛阶与表7的误差收敛阶相同,符合理论分析。 表7 矩形公式外推误差估计 表8 后验误差估计 通过矩形求积公式近似计算二维柯西主值积分得到误差展开式。通过构造序列来逼近奇点,设计外推算法获得更高的计算精度,并得到了后验误差估计。这种方法也可以推广到多维柯西主值积分。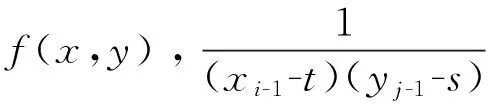
2定理的证明


3外推法

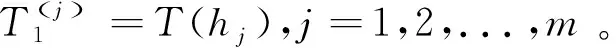
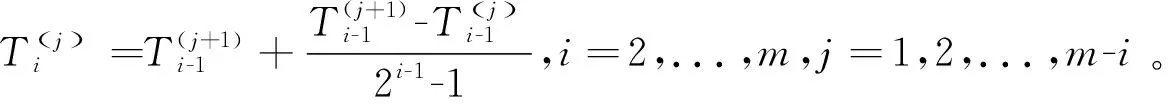
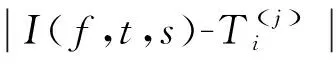
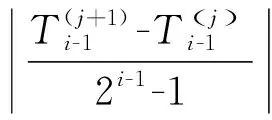
4数值算例

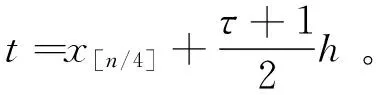


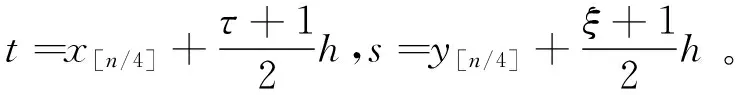




5结论

