基于次分数布朗运动的欧式回望期权定价*

张萌 温鲜 霍海峰*

(广西科技大学 理学院，广西 柳州 541004)

期权作为一种最常见的金融衍生产品，具有套期保值的作用，深受广大投资者的青睐，其定价问题也被许多学者关注。1973年，基于几何布朗运动的Black-Scholes[1]模型(简记为:B-S模型)问世，为决策者研究期权定价提供了重要依据。在此基础上，Merton[2]用傅里叶变换法给出了欧式标准看涨和看跌期权的定价显式公式，进一步丰富了期权定价的理论。由于B-S模型的市场假设非常严格，无法有效反映标的资产价格的长期相关性，也不符合金融资产收益率具有“尖峰厚尾”的分布特征[3]。为了得到更能反映实际金融市场的期权定价模型，众多学者从不同角度对Black-Scholes模型进行推广，如随机利率模型[4]、跳跃扩散模型[5]、分数次Black-Scholes模型等[6]。由于分数布朗运动不是半鞅[7]，无法使用已有的随机积分理论对其进行分析，为了更有效地刻画标的资产价格的变化过程，Bojdecki等[8]研究了呈现长程相关的次分数布朗运动。对比分数布朗运动，次分数布朗运动是一种更为普遍的高斯过程，可以用来刻画金融资产的随机波动性[9]，例如，Tudor[10]发现次分数布朗运动的退化速度要快于分数布朗运动，可以更好地刻画金融资产的长记忆性。肖炜麟[9]等使用偏微分方程的方法，得到了备兑权证定价公式，并给出了参数估计的表达式。近年来，次分数布朗运动已经被引入到期权定价模型，例如两值期权[3]、亚式期权等。

不同于已有期权定价[3-11]研究，回望期权是一种强路径依赖型的奇异期权[12]，投资人在期权到期日时，以有效期内最低价格买入或者以最高价格卖出标的资产，具有比普通期权更高收入、更大风险、更受投资者的青睐等特点。1979年，Goldman[13]给出了基于Black-Scholes模型下浮动执行价格型欧式回望期权的定价解析式。在此基础上，Broadie[14]使用格点法来确定离散和连续时间下，路径依赖型期权的准确价格。学者们对Goldman模型进行推广，生成了一系列模型：有交易费用、随机利率下的、CIR模型下的回望期权定价[15]、非仿射随机波动率的欧式回望期权定价[16]等，但这些模型都以布朗运动为基础，无法有效刻画标的资产价格的长记忆性。因此，基于次分数布朗运动的定价模型研究回望期权具有一定的实际意义和应用价值。 首先针对浮动执行价格型欧式回望期权，以次分数布朗运动为基础构造股票价格满足的次分数B-S模型。基于此模型，利用投资组合计算得到欧式看跌回望期权满足的偏微分方程。结合边界条件，经过一系列数学变换，将此方程转化为经典的热传导方程，并利用泊松公式求出求其价格显示解。最后，以钢钒PGP1权证数据为例，估计参数H和σ值，讨论参数σ和H变化对回望期权价格的影响。进而分别计算次分数B-S模型和标准B-S模型的回望期权价格，并进行比较说明。从理论推导和数值计算方面丰富了回望期权的定价理论，对于金融衍生产品的风险控制具有重要实践意义。

1 次分数Black-Scholes 模型

考虑一个零摩擦、零套利的金融市场，风险中性概率下股票价格( S )[17]满足的随机微分方程为：

(1)

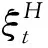
(2)

2 主要结果

(3)

其中N(·) 表示标准正态分布函数，且:

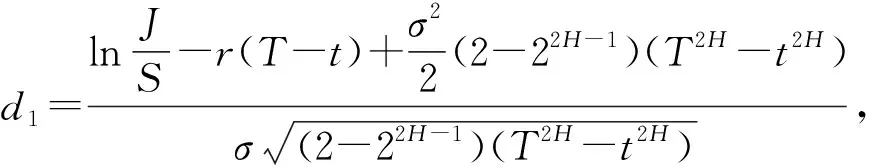
证明：浮动执行价型欧式回望看跌期权的价格服从下列偏微分方程：

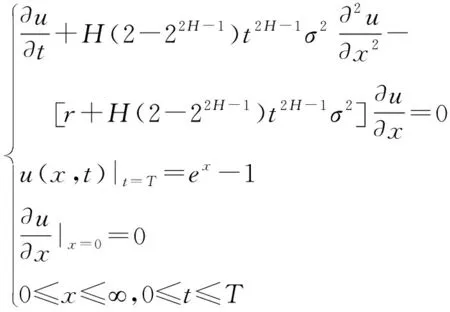
经过如下变换(2)令ω=u,η=x+α(t),τ=ρ(t)整理得：

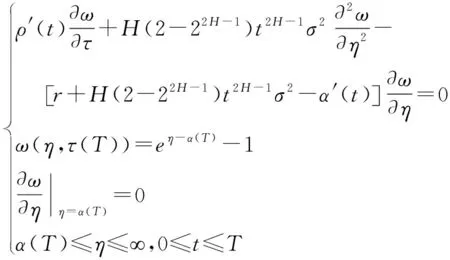
有

(4)

原方程转化为热传导方程，在{η∈R,0≤t≤T}上有：

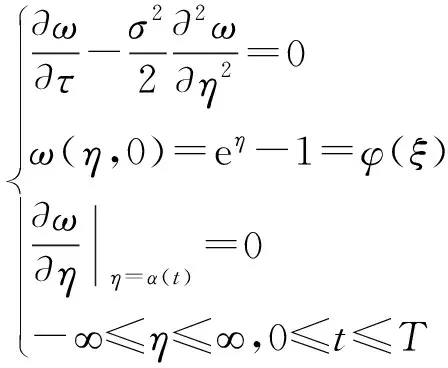
上述Cauchy问题结合Poisson公式可求得：

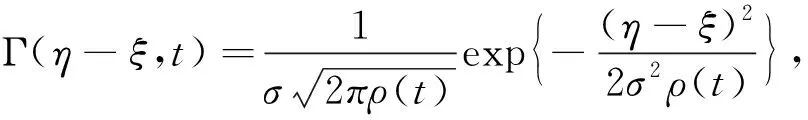
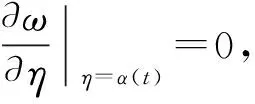
将其代入泊松公式得：

整理得：

结合变换(1)和(2)以及公式(4)，还原可得：

其中d1,d2,d3,θ如定理1所示。

定理2若股价满足次分数Black-Scholes模型(1)，欧式浮动执行价型回望看涨期权的价格为：

(5)

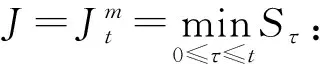
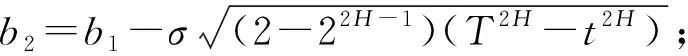
证明：类似定理1证明。

3 数值计算

以2005年12月5日到2007年4月23日钢钒PGP1权证数据为例，进行模型参数估计，如表1所示。

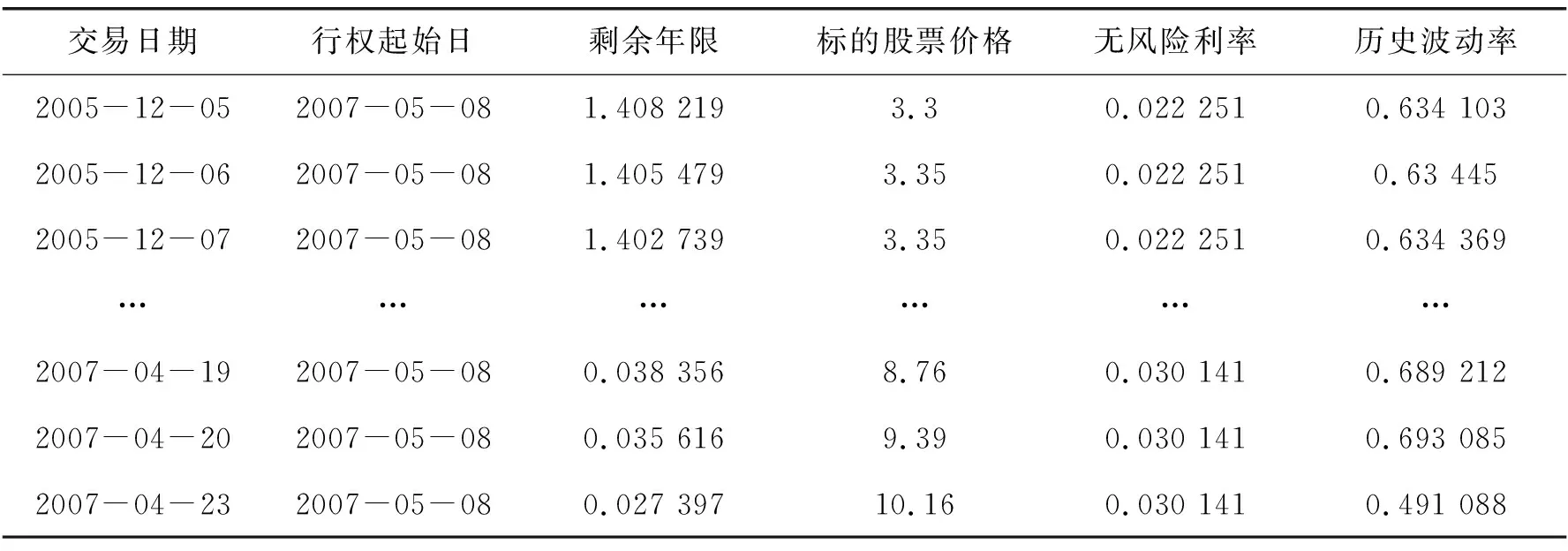
表1 钢钒PGP1权证部分数据

采用文献[9]估计方法：

(6)

(7)

表2 欧式回望期权数值计算结果

由表2可知，基于次分数B-S模型的欧式回望期权价格在各时期略高于经典B-S模型的期权价格。表3展示了两个模型下期权价格的基本统计信息，基于次分数B-S模型计算的欧式回望期权平均价格较高且变异系数较低。

表3 两个模型下的基本统计信息

基于次分数B-S模型，讨论参数H和σ值变化对期权价格的影响。当H=0.6，σ取值分别为0.3、0.4、0.5时，计算回望期权价格。由图1可知，当σ为0.3时期权价格最高；σ为0.5时期权价格最低，即当H不变时，期权价格随着σ的增大而减小。

图1 不同σ的期权价格

当σ取不同值时，期权价格的平均值、标准差、变异系数等基本统计指标，见表4。当σ取0.3时期权平均价格最高，并且期权价格离散程度最低；σ取0.5时期权平均价格最低，且离散程度最大。

表4 不同σ期权价格基本统计

当σ=0.4，H分别为0.5,0.6,0.7时，计算回望期权价格，由图2可知，H为0.5时期权价格最低，H为0.7时期权价格最高，即当σ不变时，期权价格随着H值增加而增加。

图2 不同H值的期权价格

当H取不同值时，期权价格的最大值、最小值、平均值、标准差、变异系数，见表5。当H=0.7时期权平均价格最高，并且期权价格离散程度最低；当H=0.5时期权平均价格最低，且离散程度最大。

表5 不同H值的期权价格基本统计

4 结论

为了更有效地刻画标的资产价格的长记忆性，采用次分数布朗运动模型，采用偏微分方程的方法求出了浮动执行价格型欧式回望期权价格的显示解，并以钢钒PGP1权证数据为例，比较次分数B-S模型和经典B-S模型的回望期权价格，结果表明：基于次分数B-S模型下的欧式回望期权价格变异系数低于经典B-S模型下的变异系数，次分数B-S模型能够更稳定地表现出欧式回望期权的价格。参数H和σ变化对期权价格的影响：当H不变时，回望期权价格随着σ的增大而减小；当σ不变时，回望期权价格随着H值增大而增大。