具有饱和发生率和Levy噪声的随机SIQS传染病模型

黎丽 陈桦剑

(1 桂林航天工业学院 理学院,广西 桂林 541004 ;2 广西师范大学 数学与统计学院,广西 桂林 541004)

传染病历来是人类健康的重要威胁之一，传染病的传播是人类社会一个极其重要的议题。众所周知，Kermack和McKendrick首次提出经典的SIR模型[1]，开启了用数学模型描述传染病的新时期。此后，越来越多学者开始使用数学模型描述传染病[2-6]。

实际上，我们的生活充满了随机性，学者们发现随机传染病模型比确定性传染病模型更符合实际情况，因此，传染病模型的研究由确定性模型逐渐向随机模型迈进，并得到了许多令人惊叹的成果[7-15]。

最近，Zhang等人提出了一个随机SIQS传染病模型[16]：

(1)

其中，模型各变量和参数意义如下：S(t)、I(t)、Q(t)分别表示易感者、染病者和隔离者在t时刻的人数；N(t)为t时刻的总人数，N(t)=S(t)+I(t)+Q(t)；β表示疾病传播速率；b、μ和α分别代表自然出生率、自然死亡率和因病死亡率；δ代表从染病者转为隔离者的速率；γ和ε分别是染病者和隔离者转为易感者的速率。B(t)是标准布朗运动，σ表示环境白噪声强度。

(2)

其中，模型(2)各变量和参数意义如下：

Λ表示人口输入常率；

β表示疾病传播速率；

μ1,μ2,μ3表示分别为易感者S、染病者I和隔离者Q的自然死亡率；

α2、α3表示分别为染病者I和隔离者Q的因病死亡率；

δ表示染病者I转为隔离者Q的速率；

γ、ε表示分别为染病者I和隔离者Q转为易感者S的速率。

Bi(t)(i=1,2,3)是标准布朗运动，σi(i=1,2,3)表示环境白噪声强度。

实际上，传染病系统可能会受到突发的环境干扰，例如地震、洪水、飓风等。这些突发现象无法用一般的随机传染病模型进行建模。Zhang和Wang提出用带跳的Levy过程描述突发现象[19]。

因此，考虑Levy噪声对模型(2)的影响，建立一项具有饱和发生率和Levy噪声的随机SIQS传染病模型：

(3)

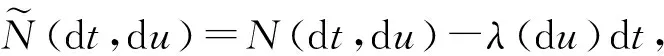
文章定义(Ω,F,{Ft}t≥0,P)是一个带参考族{Ft}t≥0的完备概率空间，并且满足一般条件({Ft}t≥0单调递增右连续，且Ft0包含所有零测集)。

本文有下列假设成立：

2 全局正解的存在性

模型(3)对应的确定性SIQS模型有

d(S+I+Q)=[Λ-μ1S-(μ2+α2)I-(μ3+α3)]dt

≤[Λ-μ1(S+I+Q)]dt,

因此，确定性SIQS模型的可行域为

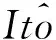
dV1=LV1dt+σ1(S-1)dB1(t)+σ2(I-1)dB2(t)+σ3(Q-1)dB3(t)+

其中

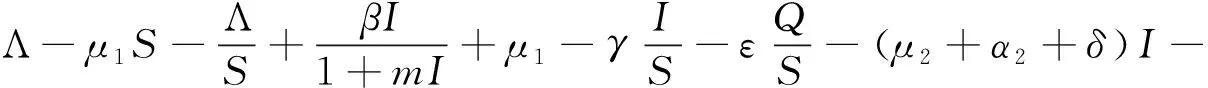
则

3 随机一致有界

记X(t)=(S(t),I(t),Q(t))为系统(3)的解。

定义模型(3)是随机一致有界的，如果∀η∈(0,1)，存在整数H=H(η)，使得模型(3)带初始值X(0)=(S(0),I(0),Q(0))的解X(t)=(S(t),I(t),Q(t))满足

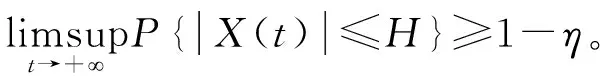
引理1[21]

xr≤1+r(x-1),x≥0,1>r≥0.

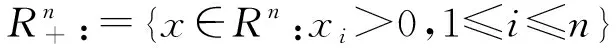
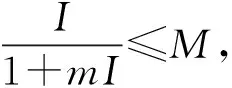
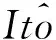
dV2(S,I,Q)=LV2dt+et(θσ1SθdB1+θσ2IθdB2+θσ3QθdB3)+

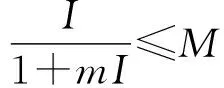
所以，有LV2(S,I,Q)≤etF(S,I,Q)。

dV2(S,I,Q)≤(etK1)dt+et(θσ1SθdB1+θσ2IθdB2+θσ3QθdB3)+

进一步，

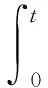
两边取期望，

E|etV2(S,I,Q)|≤V2(S(0),I(0),Q(0))+K1(et-1)，

则

EV2(S,I,Q)≤e-tV2(S(0),I(0),Q(0))+K1(1-e-t)≤e-tV2(S(0),I(0),Q(0))+K1，

表明：

结合引理1中第二个不等式，得到

模型(3)是随机一致有界的，定理证毕。

4 平衡点附近的渐近行为

对于确定性SIQS模型：

(4)

随机SIQS模型(3)与确定性SIQS模型(4)相比，无病平衡点和地方病平衡点均发生改变。本节仅讨论在模型的无病平衡点和地方病平衡点附近的渐近行为。

4.1 无病平衡点附近的渐近行为

其中

(5)

其中

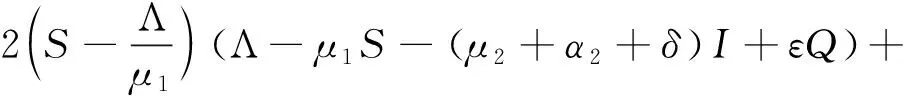
2I(Λ-μ1S-(μ2+α2+δ)I+εQ)+2Q(δI-(μ3+α3+ε)Q)+

利用基本不等式2ab≤a2+b2

所以

(6)

一方面，(5)式两边从0到t积分，取数学期望，

另一方面，由(6)式可得

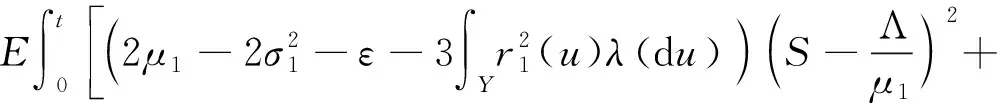
其中

定理证毕。

4.2 地方病平衡点附近的渐近行为

那么

其中

证明：当基本再生数R0>1时，有地方病平衡点E*=(S*,I*,Q*)，满足：

LV4=(S-S*+I-I*)(Λ-μ1S-(μ2+α2+δ)I+εQ)+

根据地方病平衡点E*=(S*,I*,Q*)和模型(4)可知：Λ=μ1S*+(μ2+α2+δ)I*-εQ*,

LV4=(S-S*+I-I*)(μ1S*+(μ2+α2+δ)I*-εQ*-μ1S-(μ2+α2+δ)I+εQ)+

=(S-S*+I-I*)(-μ1(S-S*)-(μ2+α2+δ)(I-I*)+ε(Q-Q*))+

=-μ1(S-S*)2-(μ2+α2+δ)(I-I*)(S-S*)+ε(S-S*)(Q-Q*)-

根据基本不等式2ab≤a2+b2

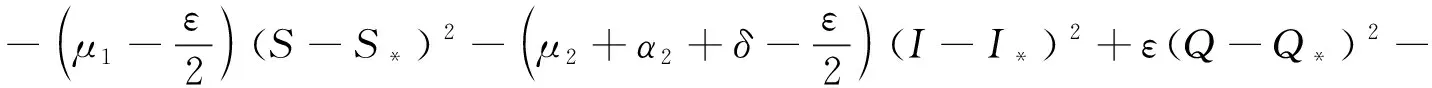
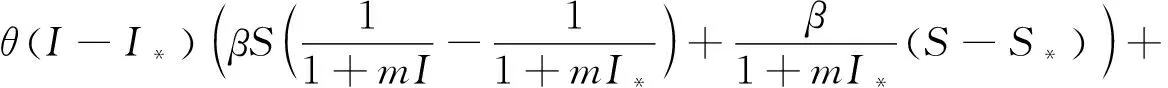
结合(μ3+α3+ε)Q*=δI*及基本不等式2ab≤a2+b2

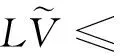
(7)

(8)

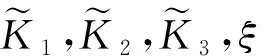
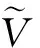
结合(8)式，令t→∞，得

定理证毕。

5 疾病的灭绝与持久

传染病的灭绝与持久是传染病研究的重点。本节定义随机模型(3)的基本再生数，给出传染病灭绝与持久的充分条件。

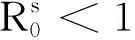
定义随机模型(3)的基本再生数

5.1 疾病的灭绝

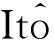
(9)

式(9)从0到t积分，并除以t，根据文献[22]引理以及强大数定理，有

因此

5.2 疾病的持久

证明：根据模型(3)有

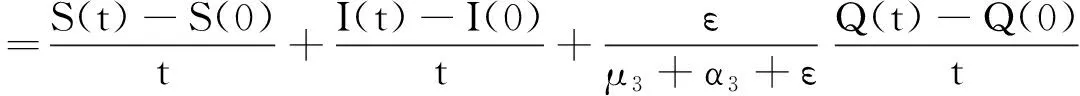
其中

经过变换，

(10)

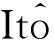
(11)

式(11)从0到t积分并除以t，

(12)

将式(10式代入式(12)，

变换后，得到

根据文献[22]引理以及强大数定理

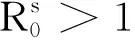
6 结论

本文提出了一项具有饱和发生率和Levy噪声的随机SIQS传染病模型，利用Lyapunov方法和Ito公式，证明了模型(3)全局正解的存在性和随机一致有界性质。

其中K2如定理3中所示。

如果R0<1，且满足一定条件，那么地方病平衡点附近有：

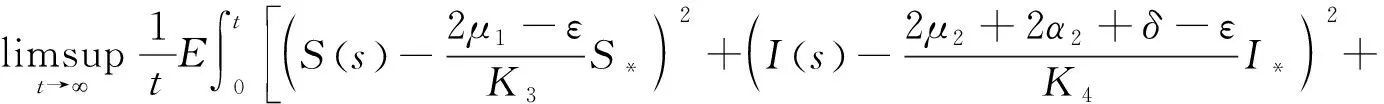
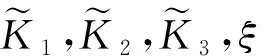
定义随机模型(3)的基本再生数