对一道椭圆试题的探究与拓展

李 霞

(甘肃省白银市第十中学)

1 题目呈现

(1)求椭圆C的方程;

(2)设A为椭圆的右顶点,直线AP,AQ分别交直线l2:x＝-4于M,N两点,试判断以MN为直径的圆是否恒过椭圆长轴上一个定点,并说明理由.

2 解法探究

解法1向量思想

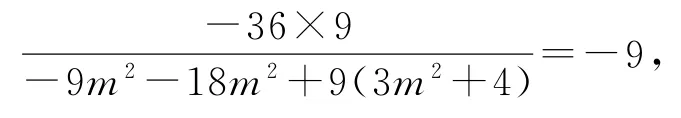
所以(t＋4)2＝9,解得t＝-7(舍)或-1.因此以MN为直径的圆恒过椭圆长轴上的定点(-1,0).

解法2相交弦定理

设MN交x轴于点Q,以MN为直径的圆交x轴于点D,E,则|QD|＝|QE|.据相交弦定理有|QN|·|QM|＝|QD|·|QE|＝|QD|2.据解法1知

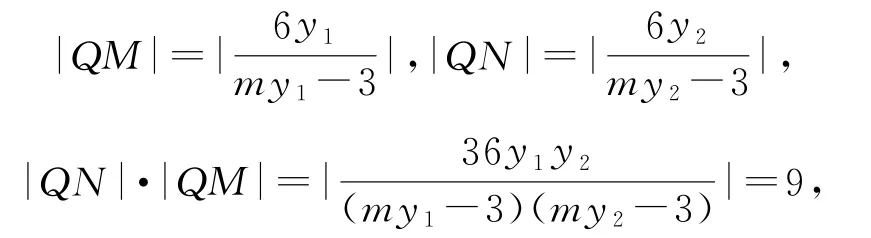
所以|QD|＝3,因此以MN为直径的圆恒过定点(-1,0),(-7,0),又点(-1,0)在椭圆长轴上,故以MN为直径的圆恒过椭圆长轴上的定点(-1,0).

3 背景探究

一般而言,圆锥曲线中的定值、定点、定线等结论都是以圆锥曲线本身所蕴含的优美几何性质为支撑,有着丰富的几何背景.探究发现,本题与椭圆的下述三条性质密切相关.

性质2如图1所示,设点A,B为椭圆1(a＞b＞0)的左、右顶点,过点T(t,0)(|t|＜a)且斜率不为零的直线交椭圆C于M,N两点,则

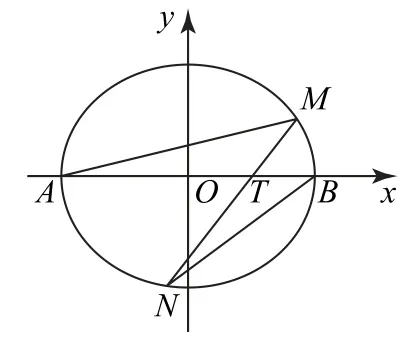
图1

性质3如图2 所示,设点A,B为椭圆C:＝1(a＞b＞0)的左、右顶点,过点T(t,0)(|t|＜a)且斜率不为零的直线交椭圆C于P,Q两点,直线BP,BQ分别交直线x＝于M,N两点,则M,A,Q三点共线,N,A,P三点共线.

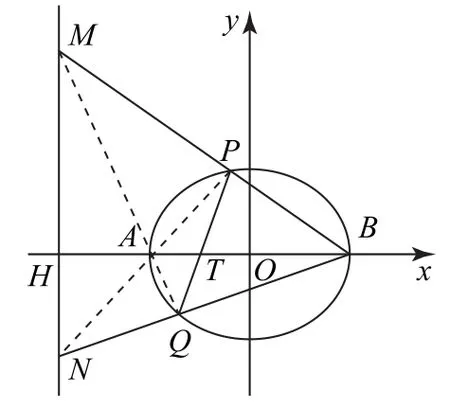
图2

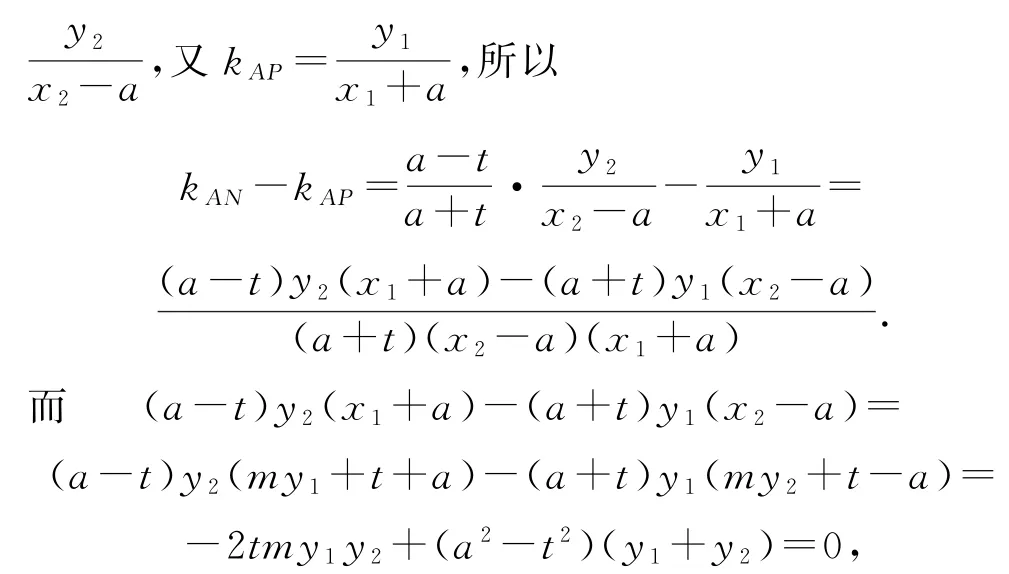
所以N,A,P三点共线.同理可证M,A,Q三点共线.

解析几何本质还是几何,在学习过程中,我们要有意识地去研究其几何结构,掌握其几何性质.

4 拓展探究

根据以上过程,可以得到一般性的结论.

结论1设点A为椭圆＝1(a＞b＞0)的左(右)顶点,过点T(t,0)(|t|＜a)且斜率不为零的直线交椭圆C于P,Q两点,直线AP,AQ分别交直线x＝于M,N两点,则以MN为直径的圆恒过定点

结论2设点A为椭圆＝1(a＞b＞0)的上(下)顶点,过点T(0,t)(|t|＜b)且不垂直于x轴的直线交椭圆C于P,Q两点,直线AP,AQ分别交直线y＝于M,N两点,则以MN为直径的圆恒过定点

结论3设点A为双曲线＝1(a＞0,b＞0)的顶点,过点T(t,0)(|t|＞a)且斜率不为零的直线交双曲线C于P,Q两点,直线AP,AQ分别交直线x＝于M,N两点,则以MN为直径的圆恒过定点

结论4过点T(t,0)(t＞0)的直线交抛物线C:y2＝2px(p＞0)于P,Q两点,直线OP,OQ分别交直线x＝-t于M,N两点,则以MN为直径的圆恒过定点

(完)