改进粒子群算法在库存预测中的应用
黄育鹏,何雪明,卢立新,林自东
(1.江南大学 机械工程学院,江苏 无锡 214122;2.山东碧海包装材料有限公司,山东 临沂 276600)
库存预测是根据企业的历史库存数据,通过科学的方法和逻辑,对近期库存的水平做出推测,以此来提前应对市场以及客户方面可能出现的突发性问题。有效的库存预测能够为企业降低库存成本,为生产或者采购计划提供依据[1]。因此库存预测也是个企业重点关注的问题之一[2-3]。
而预测的方法也有许多,常用的就有灰色预测(grey prediction,GM)、简单平均(simple averaging,SA),加权平均(weighted average,WA),简单移动平均(simple moving average,SMA),加权移动平均(weighted moving average,WMA),指数平滑(exponential smoothing,ES)等算法,张林灵等将二次指数平滑模型和灰色马尔科夫模型组合起来,为低值医用耗材的库存准备提供了可靠依据[4]。李佳民利用简单移动平均法对汽车售后配件需求进行预测,推断未来发展趋势,为汽车服务企业提供参考和借鉴[5]。张硕等利用加权移动平均法预测某产品未来3个月的销售量[6]。杨博帆等以动态多模型指数平滑法对传感器测量参数进行实时预测[7]。伍信怡等以指数平滑法模型与季节性差分自回归移动平均模型对通过三峡船闸货运量建立了预测模型[8]。刘奇等通过改进的蝗虫优化算法构建了一个血站供应的预测模型[9]。Maguluri等基于聚类的非线性回归算法构建了一个预测股票价格趋势的数据模型[10]。Dai等采用SOP以及GM算法构建了一个预测股票收益的模型[11]。
课题组采用粒子群算法并对其进行改进,以改善其早熟的问题,增强全局搜索能力。结合三次指数平滑法构建库存预测模型,通过求解最佳平滑系数,使该系数能够自适应地调整以匹配当前历史数据,预测下一期的库存值。并通过某汽车零部件公司生产的一种导流板6个月的实际库存数据来验证该预测模型的可行性。
1 粒子群和指数平滑算法原理及缺点
1.1 粒子群算法原理及缺点
粒子群算法(PSO)是1995年,Eberhart博士和Kennedy博士在对鸟群捕食进行观察时,发现鸟群在捕食时存在一定的规律,进而提出了PSO这一群智能寻优算法。该算法中所有的粒子都被认为是在解空间(即解的范围)中的一个可行解,而每个粒子都会被一个速度v来决定他们飞行方向和速度,并且每个粒子都会知道自己当前寻找到的最好的位置(pbest),以及目前整个群体中找到的最好的位置(gbest)。就这样,在不断迭代更新中,每个粒子通过向pbest和gbest方向靠拢来更新自己在解空间中的位置,直到满足退出要求,以此得到最后的最优解。粒子位置的更新公式为:
(1)
(2)

PSO算法的主要流程如下:
1)初始化粒子群,包括每个粒子的x(粒子位置)和v(粒子速度);
2)计算每个粒子的适应度值F;
3)将当前粒子的F和个体极值pbest比较,如果F 4)对每个粒子,用它的适应度值F和全局极值gbest比较,如果F 5)根据式(1)和式(2)更新粒子的速度v和位置x; 6)如果满足结束条件(到达最大循环次数)退出,否则返回步骤2)。 粒子群算法存在的缺点主要有:过于早熟,容易陷入局部最优解。 指数平滑法ES是由布朗提出的一种时间序列分析预测方法,该方法实际上是一种特殊的移动加权平均法,他每一期的指数平滑值都是当前的实际观察值与前一期指数平滑值的加权。以数学公式来表达即为: yk=αxk-1+(1-α)yk-1。 (3) 式中:yk为第k期的预测值;xk-1为第k-1期的实际观察值;yk-1为第k-1期的预测值;α为平滑系数,该系数越大则代表当前的实际值对预测值的影响较大,反之较小。 指数平滑法分为一次、二次和三次指数平滑法。一次主要用于比较平稳的数值序列,二次主要用于呈线性趋势的数值序列,三次则用于波动较大,有明显趋势性以及季节性的数值序列。文中采用三次指数平滑法,并且为调整该方法预测值的滞后性,将放弃传统的以(xk-1-yk-1)2产生的误差平方和(SSE)作为评价指标,将(xk-2-yk-1)2产生的误差平方和作为评价指标。 三次指数平滑法的计算公式为: (4) (5) (6) 预测n期数值的公式为: Yt+n=at+btn+ctn2。 (7) 式中at,bt和ct为第t期的预测参数。 其中: (8) 指数平滑法的缺点主要是平滑系数一经确定就是固定值,无法更改,后期预测精度会下降。 在PSO算法中,惯性权重w是一个极其重要的调整参数。w较大时能够使得算法具有较大的全局搜索能力,w较小时能够提升算法的局部搜索能力。常见的w变化方式主要有线性递减权重法和随机权重法等。课题组引入正割三角函数来自适应地改变w,公式如下: (9) 式中:wmax为惯性权重最大值,wmin为惯性权重最小值,t为当前迭代次数,T为最大迭代次数。 随着迭代次数的不断增加,w会有最大值不断非线性减小到最小值,以此达到非线性调整w的目的。 学习因子c1,c2一般为固定常数,且通常取的值为2,本研究中学习因子采用异步变化的形式,使得在算法迭代初期,粒子能够拥有较大的自我学习能力和较小的社会学习能力,以此来增强全局搜索能力;后期则相反,粒子具有较小的自我学习能力和较大的社会学习能力,以此来使得解能够收敛,公式如下: (10) 通常粒子的更新公式如式(2)所示,课题组引入海鸥算法(SOA)中避免碰撞的一个变量A,以此来增强粒子的多样性,公式如下: A=fc-(t·fc/T)。 (11) 式中fc为控制因子,设为2。 则位置更新公式如下: (12) 课题组使用4种常用的算法性能测试函数,通过与原始PSO算法、SOA算法对比,来验证改进后算法的性能。测试函数表如表1所示。 表1 测试函数表 参数设置: 1)原始PSO。粒子数目N=50,最大迭代次数M=1 000,空间维数D=30,惯性权重w=0.5,c1=c2=1.5。 2)SOA。种群规模N=50,最大迭代次数M=1 000,空间维数D=30,螺旋参数vsp=u=1,频率fc=2。 3)改进PSO。粒子数目N=50,最大迭代次数M=1 000,空间维数D=30,惯性权重wmax=0.9,wmin=0.4。 对每个标准函数的适应度值测试20次后取平均值,平均值越接近表1中的理论值0则表示效果越好,结果如表2所示。 表2 测试函数结果 各测试函数迭代效果如图1~4所示。 图1 Sphere的最优个体适应度 图2 Schwefel2.22的最优个体适应度 图3 Rastrigin的最优个体适应度 图4 Ackley的最优个体适应度 通过效果图1~4,以及测试出来的平均值可知改进后的PSO算法在精度、搜索能力以及收敛能力都比原始PSO以及SOA算法要好。 课题组选取的改进PSO算法的参数为:种群规模为100,最大迭代次数为300,空间维数为1维,wmax=0.9,wmin=0.8。 三次指数平滑法的初始值参数选取主要有2种方式。 1)当历史的数据项较多时(t>12),忽略初始值对后期预测值的影响,此时初始平滑值应为: (13) 2)当历史数据项较少时(t≤15),为减少初始值的选定对后期预测值的影响,于是将前3期的平滑值改为: (14) 课题组选取的是第2种方式。 平滑系数α的取值范围一般为0.0~0.8,主要适用于表3的3种序列情况。 表3 不同α的分类 课题组选取α的范围为0.2~0.8。 课题组利用改进后的粒子群算法寻优能力,以误差平方和最小作为评价目标,来自适应调整α的值,让其能够不断适应当前的数据波动情况。 步骤1:在0.2~0.8范围内初始化粒子,个数为100。 步骤2:将每个粒子的值作为平滑系数α以及历史库存数据代入三次指数平滑算法中根据式(4)~(8)和式(14)中计算预测值并将误差平方和返回作为当前粒子的评价函数F。 步骤3:将当前的F与pbest和gbest比较,更新pbest和gbest的值。 步骤4:更新粒子的x和v。 步骤5:再返回步骤2继续迭代更新,直到达到最大迭代次数,输出预测值。 课题组选取2020年1月至3月某公司生产的一种导流板的库存数据作为历史观察数据进行分析,库存数据如表4所示。 表4 1-3月库存数据表 根据文中建立的预测模型,将这3个月的数据代入模型中进行计算,并将通过本研究改进的模型得出的数据与常用的灰色预测(GM)、简单平均、加权平均、简单移动平均、加权移动平均以及原始三次指数平滑方法进行比较,得到预测结果如表5所示,误差平方和如表6所示。 表5 预测结果 表6 误差平方和 通过实际测试可知:通过改进的粒子群算法来不断搜索迭代,课题组构建的预测模型以最小的误差平方和为评价指标,寻找出最适合当前数据的平滑系数α,其相较原始预测模型以及常用的预测模型精度更高,更加贴近实际值,对于这种波动较大的库存预测更具优势。 课题组针对企业自动化立体仓库库存预测结果不准确、具有时间滞后性的问题,提出了一种新的预测方法:通过将改进PSO算法与三次指数平滑法相结合构建能够自适应改变平滑系数的预测模型,使企业的产品库存预测精度提高。实验结果表明: 1)通过引入非线性动态惯性权重w,学习因子c1,c2以及SOA算法中的避免碰撞变量A,增强了PSO算法前期的全局搜索能力、后期收敛能力以及粒子的多样性。 2)结合三次指数平滑法,通过自适应的调整平滑系数α,构建了一个库存预测模型,通过与其他常用的预测模型对比,构建的预测模型数值更加精确,为预测这种波动性较大的数据提供了参考。1.2 指数平滑算法原理及缺点

2 PSO算法的改进
2.1 非线性动态惯性权重
2.2 变学习因子策略
2.3 粒子位置更新策略
2.4 算法性能测试


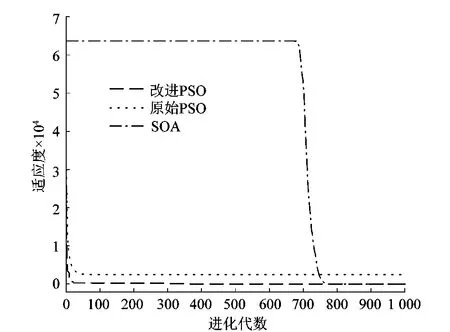
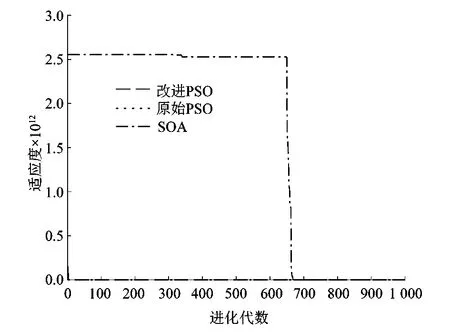
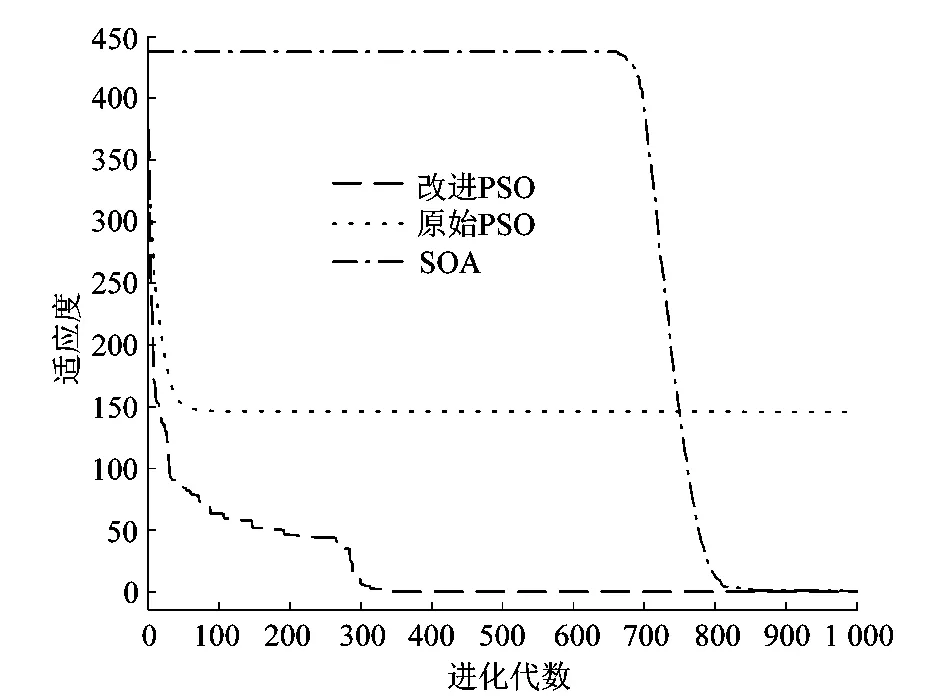
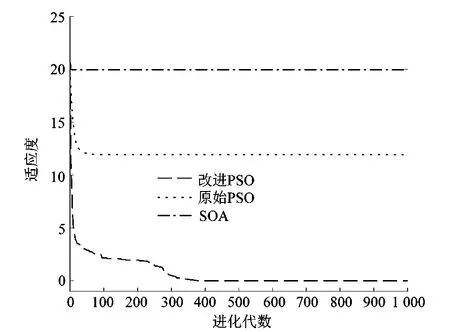
3 基于改进PSO算法的预测模型构建
3.1 参数选取

3.2 预测模型的步骤
4 实际测试及结果分析
4.1 实际测试

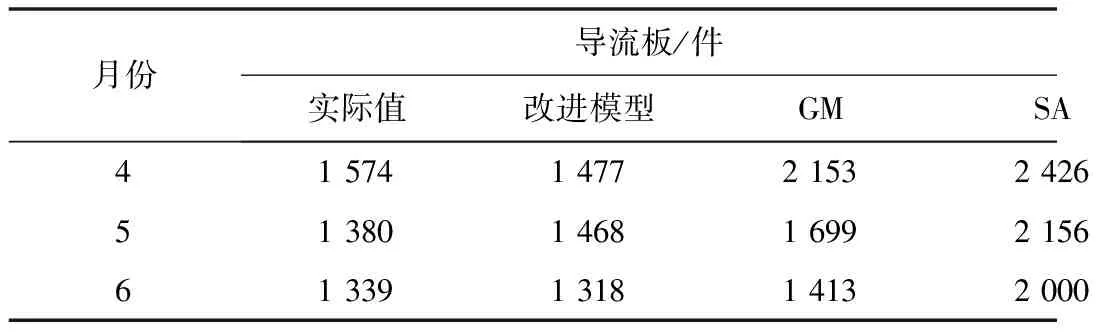
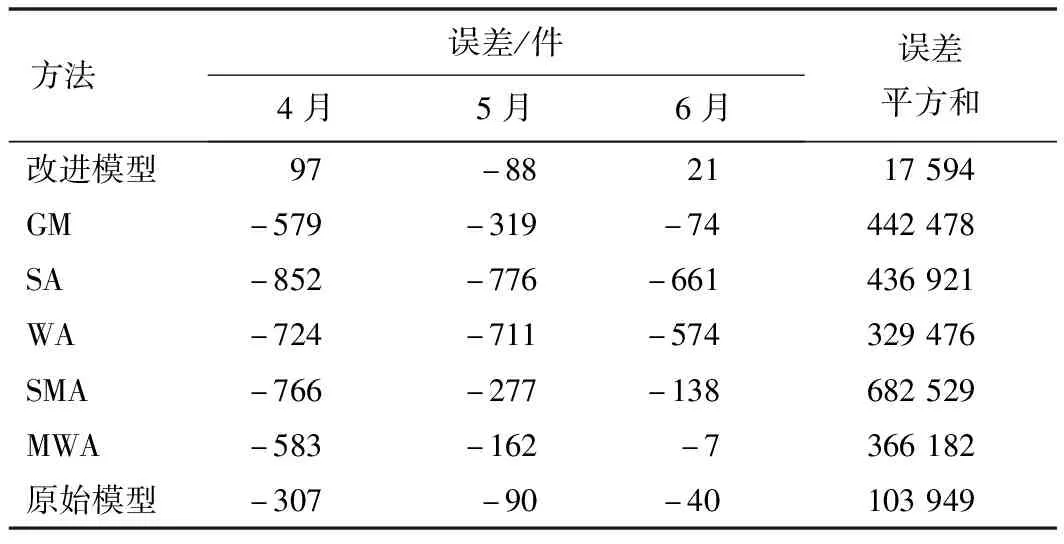
4.2 结果分析
5 结论

