基于改进蝙蝠算法的机械臂时间最优轨迹规划
李帅帅,王双园,张吴飞,李嘉成
(上海理工大学 机械工程学院,上海 200093)
随着工业机器人技术的快速发展以及自动化水平的大幅度提高,越来越多的机械臂被应用于不同的场景之中。而机器人的轨迹运动是主要的关注点之一。目前针对轨迹规划主要从2个方面进行考虑:一是从时间方面进行优化;二是从力矩方面优化。课题组准备从时间方面对机械臂的轨迹进行优化。时间最优轨迹规划不仅可以缩短机械臂按照预定路径运动的时间,还可以大大提高机械臂的工作效率。目前关于时间最优轨迹规划的研究有很多。Papadopoulos等[1]利用多项式函数对关节的轨迹进行跟踪,此方法可以让机械臂的运动轨迹曲线相对平滑,但是效果不够理想;Wei等[2]利用遗传算法对机械臂的轨迹进行最优化求解,但是该方法的迭代过程比较复杂,最优解找到之后还需要对最优解进行一系列的操作,比如编码和解码等;Chen等[3]利用一种新的算法即和声搜索算法对机械臂时间求解最优解,但是该算法在参数值以及声记忆库的取值方面和概率微调方面存在着一定的不足;Kim等[4]采用了一种标准化步长将粒子群进行初始化的方法,该算法虽然优化效果相对较好,但是随着迭代次数的增加,出现了局部收敛;南文虎等[5]把机械臂的最大速度曲线进行多重约束,然后利用修型/射靶算法对偏离实际的最大速度曲线进行矫正,从而得到时间最优轨迹;蔡永超[6]采用膜计算-粒子群算法对机械臂的关节空间轨迹进行规划求解。
在众多轨迹规划方法中,插值法因为其计算简单,使用范围最为广泛。方健等[7]利用三次样条插值法对机械臂的轨迹进行优化求解;朱世强等[8]利用七次样条曲线法对机械臂轨迹进行插值,该方法使得机械臂脉冲取得连续最优。虽然高阶多项式插值在机械臂的速度、加速度等方面取得比较好的效果,但是由于高阶多项式计算相对复杂,同时对机械臂的硬件要求相对较高,实用性较低,所以有人提出用分段的方式对机械臂进行插值。李林升[9]采用5-5-7-5分段多项式对机械臂进行插值计算并利用惩罚函数取得最优值;江鸿怀等[10]利用五次非均匀 样条法对机械臂进行插值计算并结合粒子群算法求解最优解。
以上算法大都存在局部或全局最优解的问题,导致搜索能力难以平衡,稳定性较差。故课题组采用改进的蝙蝠算法,把时间最短作为优化的目标,然后约束机械臂的速度和加速度,采用3-5-5-3分段多项式对机械臂轨迹进行插值,该方法在全局以及局部的搜索平衡方面具有明显的改善,而且该算法的参数较少,计算相对简单,与传统的蝙蝠算法相比收敛性更好,优化效果明显改善。
1 构造分段多项式
在构造函数的过程中若插值函数阶数过高会导致凸包性较差,而且计算复杂[11-13];如果阶数过低会导致速度和加速度曲线不平滑,产生突变,所以课题组采用3-5-5-3次多项式函数既可以解决凸包性差的问题也可以解决速度和加速度曲线变化不平滑的问题。
3-5-5-3分段多项式的通用公式为:
(1)
式中:θi1(t)为第i个关节第1段的三次多项式;θi2(t)为第i个关节第2段的五次多项式;θi3(t)为第i个关节第3段的五次多项式;θi4(t)为第i个关节第4段的三次多项式;ai1n,ai2n,ai3n和ai4n表示第i个轨迹的第1段、第2段、第3段和第4段多项式的第n个系数,t为时间。
4段分别对应的时间段为t0~t1,t1~t2,t2~t3,t3~t4。
分段多项式中的三次多项式起点和终点轨迹函数方程为:
(2)
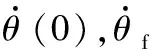
由式(2)和机械臂的速度、加速度为0的位置以及机械臂速度和加速度连续等约束条件,可以得出区间1和区间4在三次插值的轨迹函数方程的系数。同理,区间2和区间3中的轨迹函数的系数可由五次多项式函数方程解出,五次多项式的轨迹函数如式(3)所示。
(3)
2 蝙蝠算法及其改进
2.1 算法的基本原理
蝙蝠在寻找猎物时根据回声定位来检测猎物的存在。在寻找猎物时通常会以110 dB/s的声强释放大约10~20个超声波脉冲,在狩猎时音强会保持最大值;一旦发现猎物,蝙蝠就会向猎物靠近,在靠近的过程中该脉冲就会随之距离的靠近而减小,此时,脉冲的频度就会增加,通常会达到200个/s。超声波的传输与脉冲音强呈正相关,脉冲音强越大,传播距离越远,频率就越高,从而提高蝙蝠捕食的效率。
在2010年Yang根据蝙蝠的回声定位系统提出了一种仿生模拟蝙蝠猎食行为的群智能搜索算法,即蝙蝠算法[14]。蝙蝠算法把搜索空间中的各点当成是蝙蝠个体,把蝙蝠捕食时的搜索猎物和向猎物移动的过程当作搜索和优化的过程,把蝙蝠所在的位置好坏当作是求解目标的适应度值。在该算法中,如果蝙蝠想要准确无误地识别障碍物,并精准地捕捉猎物,就需要对蝙蝠算法做理想假设[15]:
1)蝙蝠捕食时利用回声定位来感知猎物与自身之间的距离,并且在障碍物识别中有着自己的独特方式。
2)蝙蝠在空间Xi中并以速度vi随机飞行,同时在固定频率fmin,可变波长λ以及音量A0下进行搜索猎物;蝙蝠会根据自身与猎物之间的距离来调整脉冲波长和频率,以更好地识别和捕获猎物,脉冲发射率γ是[0,1]之间的随机数。
3)假设在蝙蝠算法中,音量从最大值A0变化到一个固定值Amin。

fi=fmin+(fmax-fmin)β;
(4)
(5)
(6)
式中:fi为第i只蝙蝠发出的声波频率;fmax为第i只蝙蝠发出的频率最大值;fmin为第i只蝙蝠发出的频率最小值,即固定频率;x*为蝙蝠当前所处的最优位置;β为[0,1]之间的随机数。
在局部搜索中,如果一个蝙蝠选择了一个最优解,此时该蝙蝠将在此最优解的附近产生一个新的解:
xnew=xold+εAt。
(7)
式中:xold为从当前最优解中所选择的一个最优解;At为在t时刻所有蝙蝠响度的平均值;ε为[0,1]之间的随机数。
蝙蝠在搜寻猎物时会依据自身与猎物之间的距离随时调节超声波的响度以及频度,用来提高捕食的效率。蝙蝠的脉冲响度Ai和脉冲频率ri公式为:
(8)
(9)
式中:α为蝙蝠声波强度的衰减系数,0<α<1;γ为蝙蝠脉冲频度的增强系数,γ>0。
2.2 算法的基本流程
蝙蝠算法的具体流程:
1)初始化参数——最大脉冲响度A0、最大脉冲速率r0,脉冲频率范围,声波强度衰减系数α,脉冲频度增强系数γ,最大迭代次数M以及目标函数f(x)。
2)随机分布蝙蝠的位置Xi,计算当前位置的适应度值并进行比较,从而寻找最优解X*。
3)根据式(4)~(6)更新并计算蝙蝠的脉冲频率、位置和速度。
4)生成均匀分布的随机数d1,如果d1>ri,则随机扰动当前位置上的蝙蝠,让其产生新解。
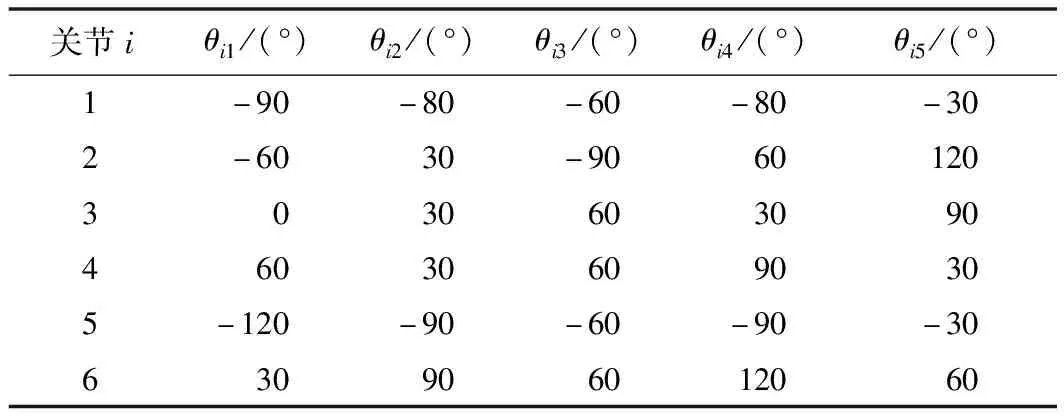
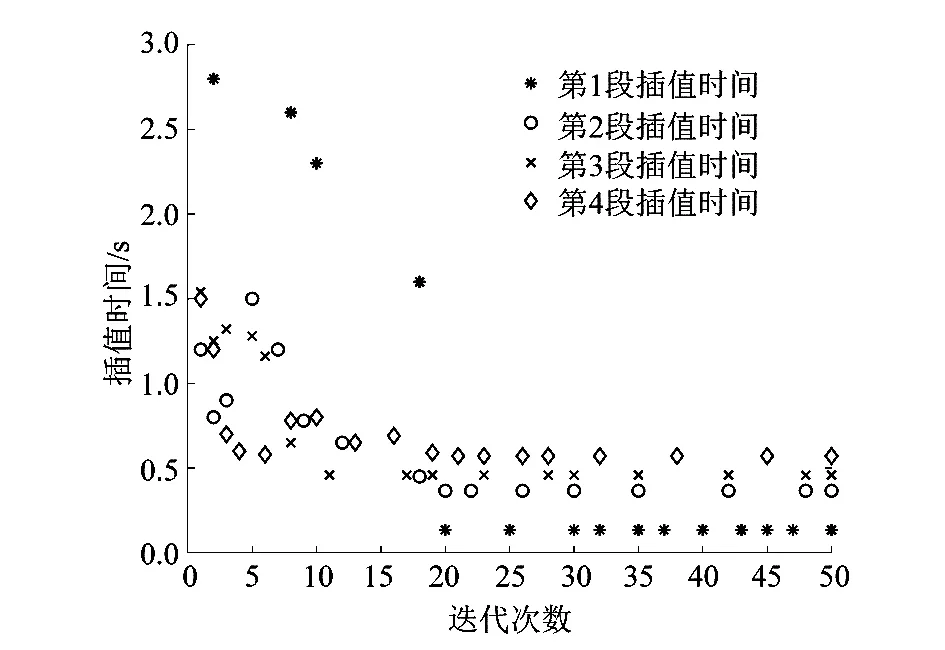
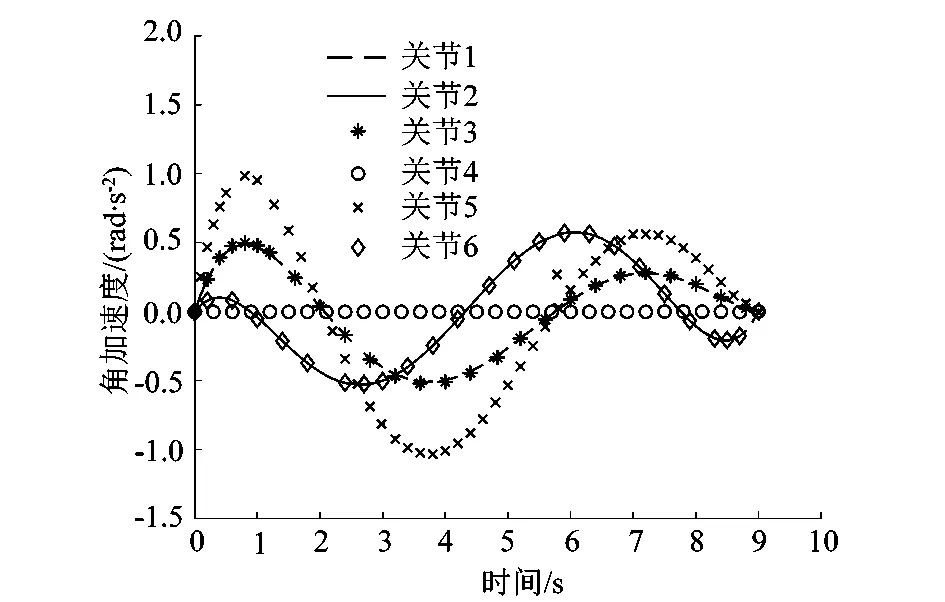
5)生成均匀分布的随机数d2,若d2 6)对所有位置上蝙蝠的适应度值进行比较,找出最优解和最优值。 7)若在当前位置不是最优解则重复步骤2)~5),直至找出最优解。 蝙蝠算法的流程图如图1所示。 图1 蝙蝠算法流程图 蝙蝠算法虽然构造模型比较简单,参数设置较少,但是很容易在迭代后期进入局部最优解,影响种群的多样性。所以为了解决传统蝙蝠算法的缺点,就需要对此算法进行改进。谢健等[16]提出了一种带Lévy飞行特征的蝙蝠算法,在该算法中用式(10)来替换蝙蝠算法中的位置更新公式。 (10) 式中Levv(λ)为蝙蝠跳跃的步长。 但是步长的控制不易确定,如果步长太小则改进没有意义,如果步长太大,则蝙蝠可能跳跃到很远的位置,所以在此基础之上对步长做出改进。在蝙蝠的步长中引入一个非线性因子η,该非线性因子可以扩大蝙蝠的搜索范围,以此可以保证在迭代后期蝙蝠种群的多样性。 (11) η=xy-0.5x; (12) (13) 式中:y为[0,1]上的随机数,p为当前的迭代次数,Tm为最大的迭代次数,e为自然常数,x为收敛因子。 从式(13)可以得出随着迭代次数的增加,x呈非线性递减。在迭代初期,x递减速度较慢,蝙蝠可以以较大的步幅向猎物移动;在接近猎物时,收敛因子衰减速度增加,此时步幅减小,从而可以更加准确地捕捉猎物,寻找最优解,可以有效地平衡全局与局部的搜索能力。 在求解机械臂时间最优轨迹时,课题组采用的3-5-5-3分段多项式法的求解与插值时间间隔t1,t2,t3和t4有关。在满足速度、加速度的前提下以时间最短为优化目标,若要使机械臂的末端快速到达某一点,就需要所有关节同时运动并同时到达某一点。优化每个关节时,应选择每一段所花费的最大时间,这样才可以保证每个关节同时到达所对应的角度。目标函数与约束条件为: (14) max {|Vi|}≤Vimax。 (15) 式中:Vi为第i个关节角速度的值,Vimax为第i个关节角速度所允许的最大值。 课题组以6自由度SCARA机械臂为研究对象,设置蝙蝠的数量为30只,最大迭代次数设置为50,音量衰减系数α=0.8,速率增强系数γ=0.3,声波响度A0=0.5,脉冲发射速率r0=0.25。选取5个路径点作为插值点,然后通过运动学逆解,将5个插值点从笛卡尔空间变换到关节空间,如表1所示。 表1 机械臂关节空间插值点 根据蝙蝠算法的步骤,限制关节的最大运行速度为1.5 rad/s,把5个插值点带入到改进的蝙蝠算法中可以得到机械臂6个关节的最优时间,如表2所示。 表2 机械臂各关节的最优时间 如果使得各关节同时到达某一点,则需要选取各关节每段插值中的最大值,所以ti1=0.354 6 s,ti2=0.427 6 s,ti3=0.526 8 s,ti4=0.570 9 s。经过改进的蝙蝠算法对3-5-5-3多项式插值之后,可以得到各关节的适应度曲线以及位置进化曲线,从图2中可以看出改进的蝙蝠算法在收敛性以及优化效果都比传统的蝙蝠算法效果要好。图3~5表示的是机械臂前3个关节的位置进化曲线图,关节1 的位置进化大概从第18次迭代开始收敛,关节2 的位置进化大概从第20次迭代开始收敛,关节3 的位置进化大概从第22次迭代开始收敛。 图2 适应度值曲线图 图3 关节1位置进化曲线 图4 关节2位置进化曲线 图5 关节3位置进化曲线 机械臂的角度、角速度和角加速度的变化曲线如图6~8所示。从图中可以看出各曲线变化相对平滑,而且曲线连续,没有发生突变。从图7可以看出机械臂的所有关节角速度均小于1.5 rad/s;图8中的关节起始加速度和终止加速度均为0,符合约束条件。 图6 角位移曲线 图7 角速度曲线 图8 角加速度曲线 课题组以SCARA 6自由度机械臂为研究对象,在关节空间下采用3-5-5-3多项式插值方法,并采用改进的蝙蝠算法求解机械臂的时间最优轨迹。利用MATLAB仿真模拟,从蝙蝠的位置进化曲线以及适应度值的对比可以看出,改进后的蝙蝠算法在收敛性以及优化性方面均远远优于传统的蝙蝠算法;从机械臂的角位移、角速度和角加速度曲线可以看出,曲线变化平稳,无突变,进一步证实了该算法的可行性。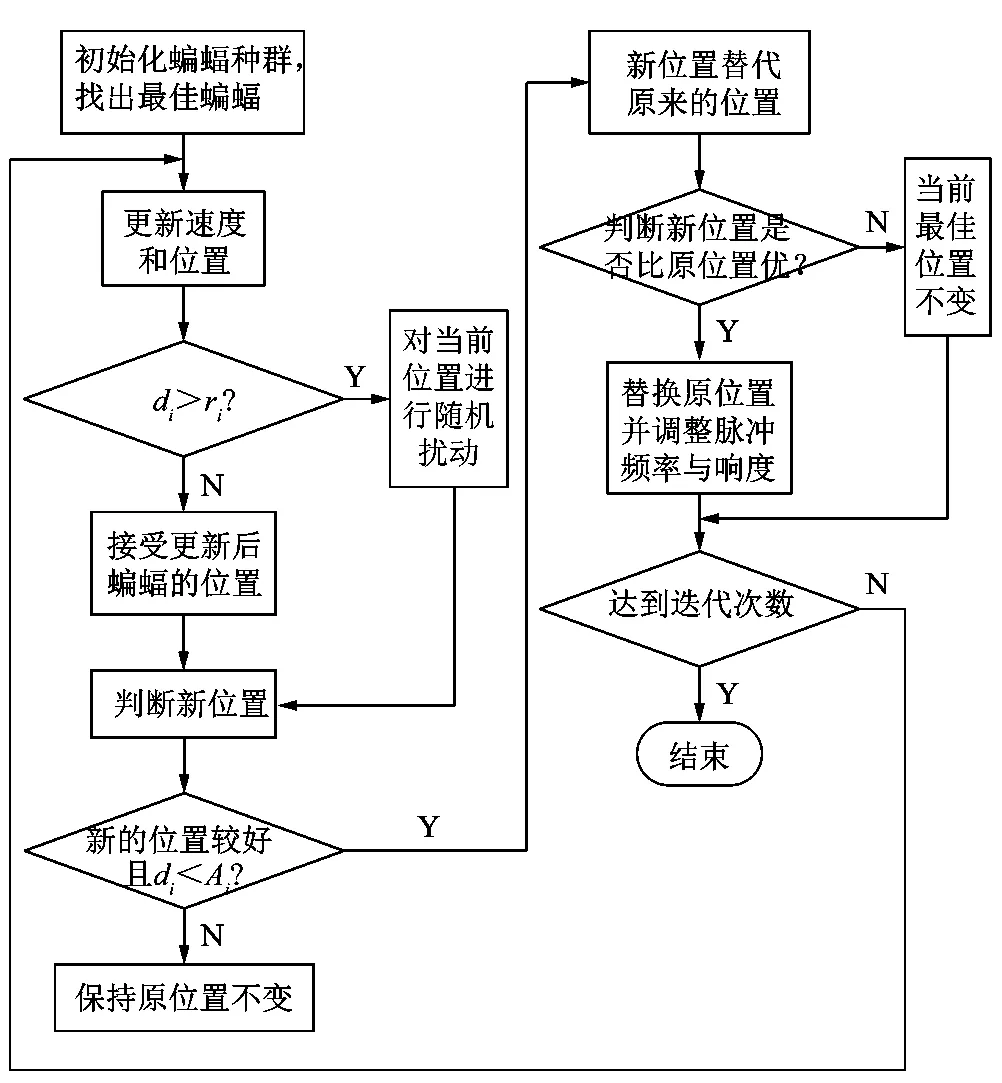
2.3 蝙蝠算法的改进
3 MATLAB仿真






4 结论

