基于多主体博弈的综合能源系统运行优化方法

王永利,刘 振,薛 露,蔡成聪,刘 琳

(华北电力大学经济与管理学院,北京 102206)

1 引言

随着煤炭、石油等化石能源的大量消耗,全球能源危机日益加剧,排放出的大量二氧化碳导致气候变暖问题不断恶化[1].基于此,我国提出了30·60双碳目标,旨在应对气候变化,实现低碳发展,而要想实现此目标须提高能源利用效率,加大可再生能源的消纳,传统的能源供应形式无法满足以上要求.综合能源系统(integrated energy system,IES)是一种将冷、热、电、气等多种异质能源相互耦合的供能系统,“横向多能互补、纵向源–网–荷–储协调”的特性可显著提高能源利用效率、降低系统运行成本,减少二氧化碳排放[2].基于此,国内外许多学者对综合能源系统进行了大量研究.

在综合能源系统建设方面,文献[3]提出了一种考虑投资约束的综合能源系统规划优化方法,可有效降低后期运行成本.文献[4]以广义多能流模型为基础,对综合能源系统多阶段规划优化进行了研究.文献[5]提出了一种基于多维相关场景集生成方法的多目标随机规划方法.以上研究对综合能源系统的建设提供了理论依据,但多适用于项目建设的前期规划,无法应用于已有的能源系统.

在综合能源系统运行优化方面,文献[6]基于能量枢纽理论,引入动态热电比概念,对能量耦合问题进行深入研究.文献[7]建立热电联产系统的紧凑模型,解决综合能源系统能源供应灵活性与转换效率不协调问题.文献[8]针对系统运行的约束条件进行了详细研究,指出不同扰动类型对运行优化的影响.文献[9–10]考虑到系统运行的经济和环境效益,建立了低碳经济模型.上述研究面向的主要是终端综合能源系统,而我国目前终端用户多采用传统供能方式,实际应用较为困难.

在博弈论应用方面,文献[11]依据Shapley值法提出了基于合作博弈的风险规避策略和交易规则.文献[12]构建合作博弈决策平台以解决多园区微网利益冲突问题.文献[13]提出一种考虑电能互济的区域综合能源系统运行优化模型,并通过纳什谈判方法分配联盟利益.文献[14]提出了一种基于能源集线器的联盟博弈模型,并采用分布式联盟构造博弈算法进行求解.文献[15]提出了基于合作博弈的风光储协同优化方法,并依据Shapley值制定收益分配策略.

综上所述,现有研究主要针对综合能源系统的技术层面和主体间电能的博弈交换开展研究,而对合作的多主体之间多能耦合和利益分配问题研究较少.基于此,本文以设备运营主体通过合作博弈的方式构建综合能源系统为研究对象,考虑系统运行成本和碳排放,建立合作博弈模型,并通过改进的Shapley值法对节约的成本进行分配.通过对合作后各主体利益进行合理分配,激励更多的用户通过合作的方式构建综合能源系统,从而加速综合能源系统的落地应用.

2 多主体参与的综合能源系统

综合能源系统是一种多种能源输入、转化和输出的多层次复杂耦合系统,系统包括多种能源耦合设备[16],一般有冷热电三联供机组(combined cooling heating and power,CCHP)、地源热泵(heat pump,HP)、电制冷机组(electric refrigeration,ER)、储能装置(electric energy storage,EES)、以及风机(wind turbine,WT)、光伏(photovoltaic,PV)等可再生能源发电设备.

但目前大部分终端用户一般只拥有某种独立的设备,所以仍然采用传统的单一供能模式,无法实现多能耦合,经济性和能效水平较低.而对多个设备运营主体而言,若通过彼此间信息共享,形成一个合作联盟,共同构建综合能源系统,集中供给冷、热、电负荷,避免低效能设备的大量使用,实现能量梯级、高效利用,则可以有效提升联盟整体的经济性并减少二氧化碳的排放量.多主体合作运营模式下综合能源系统的能流图如图1所示.

图1 综合能源系统合作博弈能流图Fig.1 Energy flow chart under cooperative operation

2.1 综合能源系统合作博弈模型

参与合作的用户主体即为博弈的参与者,由全部主体合作组建的综合能源系统即为大联盟,合作博弈的特征函数在本文中为系统运行的目标函数,策略为设备的调度方案,对应的决策空间为系统运行时的各项约束.本文考虑经济性和环保性为系统的运行优化目标,分别以系统总运行成本和碳排放来衡量.

1) 经济性目标.

综合能源系统运行优化的经济性最优是指系统运行期间的总运行成本最低.

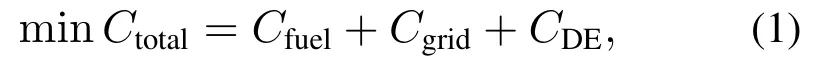
式中:Ctotal表示系统总运行成本;Cfuel表示天然气购置费用;Cgrid表示系统向电网购电费用;CDE表示设备维护费用.

2) 环保性目标.

综合能源系统运行优化的环保性目标是以系统运行期间的二氧化碳排放量最少为目标.环保性目标函数为

式中:γNG,γgrid分别为天然气燃烧和电网购电的二氧化碳排放系数.

综合能源系统是一种多能协调的供能系统,为保证用户的用能稳定性且用能成本最低,需要使系统的冷、热、电负荷达到供需平衡,同时系统中的各种供能设备在运行过程中必须满足自身的运行约束[18].以上共同构成了综合能源系统运行的约束条件,具体如下:

1) 电功率平衡约束.

2) 热功率平衡约束.

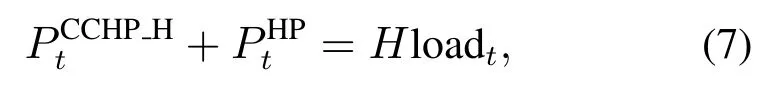
3) 冷功率平衡约束.

4) 设备安全运行约束.

5) 储能电池出力约束.

式中:SOCt为t时段EES荷电状态;SOCmin和SOCmax分别为荷电状态的最小、最大约束;Pch和Pdis分别为t时段EES充放电功率;Pch,max和Pdis,max分别为充放电功率最大约束;CEES为储能电池容量;ηch和ηdis分别为电池充放电效率.

综上所述,对于联盟I来说,其合作博弈的模型为

2.2 利益分配方法

根据本文构建的合作博弈模型,可以分析当大联盟中某些参与者离开大联盟组成新的子联盟后,两个子联盟优化各自系统运行时必然会由于设备间无法紧密耦合等原因造成资源浪费或短缺,从而都会大幅增加系统供能费用,因此有

可以判定本文构建的合作博弈模型的特征函数满足如下条件:

因此本文构建的综合能源系统合作博弈模型具有超可加性[19],系统内所有参与主体构建的大联盟具有最低的用能成本和二氧化碳排放量,也即为合作博弈的最优解.

下面就需要对合作博弈后节约的成本进行分配.Shapley值法是用于解决合作博弈时利益分配或费用分摊的一种博弈方法[20].

Shapley值的分配思想是:博弈主体(综合能源系统各设备运营商)的利益分配值等于该主体对其参加的所有联盟的边际贡献之和,具体为

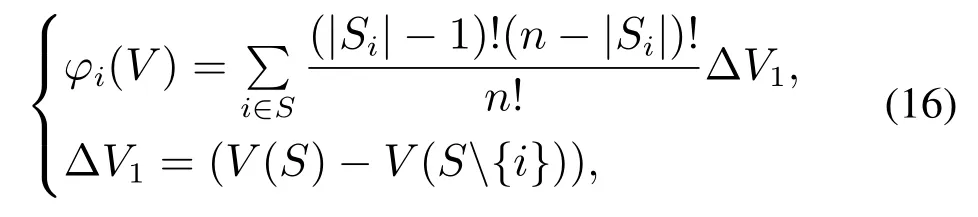
式中:φi(V)为第i个主体的利益分配值;Si为联盟中参与方的数量;n为综合能源内总参与方数量;V(S)为综合能源合作联盟的整体运行协调收入;V(S{i})为联盟S除去i后合作联盟的运行协调收入.

而上述的Shapley值法仅考虑各主体对联盟的单一贡献,忽略了协调运行中主体做出的其他方面的贡献.就综合能源系统而言,除了经济性,对碳减排等方面的贡献也是重要的因素,所以对有多维贡献的主体应当给与更多利益,以激励其他主体加大碳减排力度等.因此,在边际贡献中加入碳减排收益.基于以上思路,基于综合边际贡献值的收入分配V(i)的计算方法为

式中:V(i)是主体i基于综合效益贡献分配获得的实际收入;Vc是综合收益分配值;V(Sc)是综合能源合作联盟的整体运行协调获得的综合收益;V(Sc{i})为联盟S除去i后合作联盟获得的综合收益;V(Si,j)与V(Si,j{i})分别是主体i在合作联盟和去除i后的合作联盟中获得的综合效益的等效经济值;j是m个综合效益中的第j个效益指标.

3 求解流程及方法

本文构建的综合能源系统合作博弈模型是一种典型的非线性多目标优化问题,精确式算法难以求解,遗传算法作为启发式算法对于此类问题可以取得较好结果.但传统遗传算法[21]在求解时,交叉算子在搜索过程中存在成熟化效应,导致存在过早收敛的问题[22],为了优化此问题,本文引入相似度概念增加种群多样性,对常规算法进行改进.

具体定义为:在算法进行选择运算前,对群体中每两个个体的染色体逐位比较,设染色体长度为L,相同基因个数定义为相似度R.

设置值T为适应度平均值,即

p为种群数量.在群体中取大于T的个体进行相似程度判断.当满足如下条件时:

即认为这两个个体相似.将相似的个体中适应度低的个体滤除,剩余的个体组成新的种群,进而增加群体的多样性.经过相似性判断后,能够有效避免早熟问题的产生.

基于改进NSGA–II算法,本文研究的基于合作博弈的综合能源系统运行优化过程如下:

第1步设置系统基础数据.系统内不同设备的详细参数;冷、热、电负荷需求;电、气等能源价格;风、光等资源强度数据等.

第2步求解大联盟的合作博弈模型.采用改进的NSGA–II算法,根据策略对模型进行求解.输出优化的特征函数值及设备调度方案.

第3步对比合作构建综合能源系统与不合作两种方案下的成本和二氧化碳排放量,并将节约的成本作为要分配的利益.

第4步搜寻所有可行的子联盟.由于本文构建的合作博弈模型具有超可加性,所以系统内任意设备运营方之间只要能够满足负荷需求都可以组成不同的子联盟.

第5步求解所有子联盟的特征函数.根据第3步得出的各子联盟,采用改进的NSGA–II算法,求出各子联盟的特征函数值.

第6步采用改进的Shapley值法对大联盟利益进行分配.根据第2步和第4步得到的大联盟和所有子联盟的特征函数值,依据本文建立的改进Shapley值方法,进行利益分配.整体求解流程图如图2所示.

图2 基于改进NSGA–II算法的求解流程图Fig.2 The flow chart of the solution based on the improved NSGA–II algorithm

4 案例分析

4.1 基础数据

本文以第1章构建的多个主体为研究对象,考虑两种运营模式以验证模型有效性.运行周期为24小时,调度周期为1小时.各主体电负荷及风机和光伏出力、热负荷、冷负荷的预测结果见附录A图A1,A2,A3,分时电价及天然气价格见附录A 图A4,热网价格为0.65元/kWh,冷网价格为0.55元/kWh.设备运行参数见附录A表A1.系统采用“以热定电”的方式运行,与电网交互方式为“并网不上网”.

表A1 设备运行参数Table A1 Equipment operating parameters

图A1 电负荷及风机光伏出力Fig.A1 Electricity load and PV&WT power

图A2 热负荷Fig.A2 Thermal load

图A3 冷负荷Fig.A3 Cold load

图A4 能源价格Fig.A4 Energy prices

4.2 模拟仿真

本节基于上文建立的合作博弈模型和利益分配方法进行仿真分析,并通过对比以下两种运营模式验证模型和求解方法的有效性.

两种运营模式如下：

模式1 综合能源系统中各主体独立运行;

模式2 综合能源系统中各主体合作运行,详细运行过程见图2所示.

4.2.1 运行优化

基于以上模型,采用改进的NSGA–II算法求解综合能源系统合作博弈模型,设置种群规模为800,迭代次数为100.求解得到模式2的帕累托最优解集如图3所示.

图3 模式2帕累托最优解集Fig.3 Pareto frontier of the operation optimal results

从图中可以看出,成本最低与二氧化碳排放量最少是互相排斥的目标,一方减小必然伴随着另一方的增大,因此本文采用topsis法[23]求出其中的相对最优解,如图中标注的地方.

4.2.2 运行仿真

对于模式1,各主体独立运行,其各自运行结果如表1所示.

表1 模式1各主体运行结果Table 1 Results of the operation of each subject in mode 1

对于模式2,其Pareto最优解对应设备调度策略见附录A图A5.图例分别为:CCHP电功率(CCHP-E)、EES的充放电功率(EES)、电网购电功率(Grid)、可再生能源的输出功率(RE)、HP耗电功率(HP-E)、ER耗电功率(ER-E)、CCHP冷功率(CCHP-C)、ER的冷功率(ER)、CCHP热功率(CCHP-H)、HP的热功率(HP).从图中可以看出,储能电池在电价低谷期充电,在电价高峰期放电,充分享受了峰谷电价差,系统优先消纳可再生能源,其余设备也根据策略和能源价格,优化出了最优调度方案.

图A5 系统设备调度方案Fig.A5 Output power of each device in mode 2

4.3 仿真结果分析

4.3.1 仿真结果

根据模式1和模式2的运行调度方案,其运行结果的比较见表2.

表2 不同运行模式结果比较Table 2 Comparison of mode 1 and mode 2

从表中可以看出,与独立运行相比,各主体参与合作时,可以减少能源消耗成本2061.46元,同时减少二氧化碳排放7656.31 kg,这部分节约的成本将分配给每个联盟主体.

同时,为了验证本文提出的改进NSGA–II算法的有效性,将传统NSGA–II算法与之比较.迭代计算过程如图4所示,计算结果的精确性及求解速度比较见附录A表A2.

表A2 算法求解比较Table A2 Algorithm performance comparison results

图4 算法迭代过程比较Fig.4 Fitness curves of NSGA–II and Improved NSGA–II

结果表明,改进后的NSGA–II可以明显减少求解所消耗的时间,仅为传统NSGA–II 所消耗时间的9.56%,而且最终结果也有所优化.因此可以证明,本文提出的改进NSGA–II算法求解效率较高,且寻优能力也有所提升.

4.3.2 利益分配

由第2.2节可知,运用Shapley值法进行利益分配时,需要考虑主体对其参与的所有子联盟的边际贡献,因此首先要确定所有可行的子联盟.通过比较所有设备组合的冷、热、电负荷最大出力与各种负荷需求的最大值,确定出可行的设备组合方案即为子联盟,具体结果见附录A表A3.

表A3 所有子联盟表Table A3 All sub-affiliates details

求解所有子联盟,优化结果如图5所示.

图5 子联盟运行优化结果Fig.5 Optimization results for all sub-affiliate operations

根据两种模式优化结果和各子联盟运行结果,考虑3种利益分配方式:直接利益分配、仅考虑经济边际贡献的Shapley值法以及考虑综合边际贡献(经济性和碳排放)的改进Shapley值法.利益分配结果如图6所示.

图6 3种利益分配结果对比图Fig.6 The comparison chart of three benefit distribution results

对于分配结果结果,分析如下:

1) 储能电池主体可以享受峰谷电价差带来的收益,同时由于其可提高可再生能源消纳以及系统稳定性,降低碳排放,因此获得了高于直接分配的利益值.

2) 热泵主体直接的利益分配值为29.95元,但是根据它对联盟的经济边际贡献,多获得了一部分收益,同时由于它较高的效率降低了碳排放,最终获得了更高的利益.

3) CCHP主体的直接利益分配值为293.04元,由于其具有较高的能源利用效率以及满足冷、热负荷的主导性作用,按照经济性Shapley值法的利益分配值为481.01元,然而因其二氧化碳排放量较高,综合考虑经济性和碳减排后的利益分配值为291.28元.

4) 电制冷主体直接利益分配值为84.33元,但是由于其效率偏低,按照经济性Shapley 值法的利益分配值为54.68元,但是由于耗电供冷,二氧化碳排放量有所降低,因此最终综合性利益分配为70.04元.

5) 可再生能源主体由于其具有较高的经济性且出力无法改变,因此直接利益分配与经济性Shapley值都为260.75元,同时由于其具有较好的碳减排作用,所以最终的综合利益分配值为382.97元.

6) 电网的直接利益分配为935.83元,由于电网购电经济性较低,同时负荷的高峰时段与电价高峰时段相吻合,所以按照经济性Shapley值法的利益分配值为738.33元,但是从电网购买的电量大部分碳排放需要由发电厂承担,购电方仅承担少部分碳排放,因此可以小幅减少二氧化碳排放量,因此综合性分析下电网的利益分配值为783.45元.

经过利益分配后,每个主体的成本或者收益如表3所示.

表3 各主体成本或收入利益分配结果Table 3 Costs or revenues for each subject after benefit distribution

从表3可以看出,对于主体CCHP,HP,ER,EES和PV&WT来说,利益分配后其用能成本有所降低,对于主体Grid来说,利益分配后其收益有所增加,所以所有主体都愿意参与合作.可以证明,本文提出的综合能源系统合作博弈模型可以降低系统的总运行成本和二氧化碳排放量,利益分配方法科学有效,可以激励更多的主体合作建设综合能源系统.

4.4 敏感性分析

综合能源系统的运行成本主要受到能源价格的影响,因此有必要对系统运行成本和二氧化碳排放量随能源价格波动的敏感性进行分析.基于本文构建的合作博弈模型,以电价变化为例,对非合作和合作两种方案进行分析,综合能源系统总运行成本和碳排放量受电力价格波动变动情况结果如图7所示.

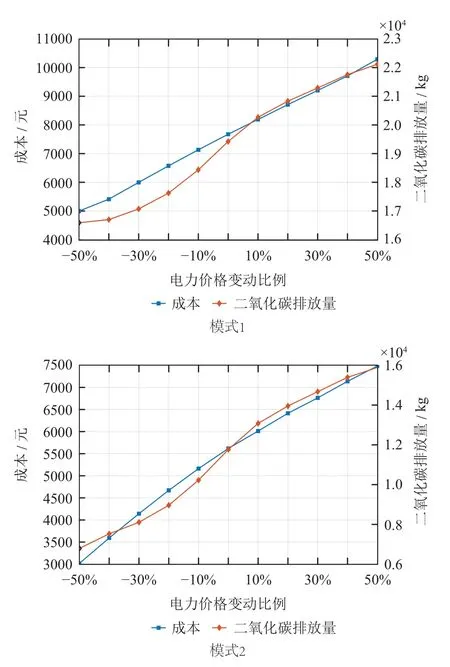
图7 不同模式电价敏感性分析Fig.7 Electricity price sensitivity analysis

模式1和模式2对比可以看出,虽然成本都与电价成正比,但是模式1中成本基本保持直线变动,而模式2在电价升高时成本增速逐渐减少,电价降低时,成本减速逐渐增加.这是因为模式1中各主体独立运行,除CCHP主体,其余主体面对电价波动无法进行有效调整,且CCHP主体自身调节能力很有限;模式2可以充分发挥不同设备的耦合替代性,在电价升高时加大CCHP出力,电价降低时减少CCHP出力.

综上所述,各主体合作运行相对于独立运行对电价上升敏感性较低,对电价下降敏感性较高,可以更有效实现“趋利避害”.

4.5 结论

本文针对不同用户通过合作组建的综合能源系统,构建了考虑系统经济性和碳排放的综合能源系统合作博弈模型,提出一种改进的NSGA–II优化算法对模型进行求解,并且采用基于经济性和碳减排的Shapley值法对联盟利益进行分配.研究结果表明:

1) 不同设备运营主体通过合作的方式构建的综合能源系统可以有效提高能源利用效率,降低系统运行成本和二氧化碳排放.

2) 本文提出的改进NSGA–II优化算法能够显著提高运行效率,同时提高寻优能力.

3) 按照本文提出的综合考虑经济性和碳减排的Shapley值法可以更加合理的对系统内各主体的利益进行分配,可激励更多用户合作组建综合能源系统.

4) 通过敏感性分析表明,基于合作博弈构建的多主体综合能源系统可以更好地应对能源价格的波动.

附录A