基于优化模拟电荷法的直流输电线路电场特性计算
于建立 张迎栋程 龙鲁志伟
(1.潍坊学院机械与自动化学院,山东潍坊 261061;2.现代电力系统仿真控制与绿色电能新技术教育部重点实验室(东北电力大学),吉林吉林 132012;3.武汉大学电气与自动化学院,湖北武汉 430072)
1 引言
超高压直流输电线路的电场特性计算是分析电磁环境的基础[1],其对输电线路的设计及运维具有重要作用.直流输电线路的电场特性计算,主要针对导线表面电场、合成电场及离子流密度.
国内外对于导线表面电场的计算,主要有马克特–门格尔法[2]、逐步镜像法[3]、有限元法[4]和模拟电荷法[5–6]等.马克特–门格尔法是将分裂导线等效为单根等效导线,研究单根等效导线的电场,此法无法反映每根分裂子导线表面电场的情况.逐步镜像法和有限元法计算电场可以达到较高的精度,但逐步镜像法需设置较多镜像电荷,计算复杂度较高.而有限元法在材料设置、边界选择及网格剖分等方面复杂度明显较高.模拟电荷法(charge simulation method,CSM)因具有无界性、原理简单、易于编程和实用性强等优点,而被广泛采用.标准模拟电荷法,通常在各子导线中心设置1个模拟电荷,其计算精度有限,不能满足工程需要.许多学者对模拟电荷法进行了优化,文献[7]用经验公式法来确定模拟电荷的位置,计算了不同数量模拟电荷的子导线表面电场,但没有分析2–5个模拟电荷的情况,且此方法并不能保证模拟电荷位置的最优.文献[8]提出自适应模拟电荷法,在子导线内设置1个模拟电荷,与标准模拟电荷法在子导线中心设置不同,其位置通过自适应法确定,此法需人为设置精度,由于1个模拟电荷可控制的精度有限,因此精度设置过高可能导致无法求解.文献[9]运用遗传算法和粒子群算法搜寻子导线内模拟电荷的最优位置,因需设置诸多参数其程序实现的复杂性较高,且参数设置的随机性易引起计算偏差.目前,众多专家学者对模拟电荷法进行了优化,但大多是对模拟电荷位置的优化,而模拟电荷数量的确定往往取决于研究人员自身的经验及其对场域的分析,因人而异的分析手段及经验难免会增加许多不必要的计算量.
对于合成电场和离子流密度的计算,主要有通量线法[10]、迭代特征线法[11]、上流有限元法[12]和有限差分法[13]等方法.其中通量线法基于Deutsch假设,因其简单高效,且能较准确预测地面合成电场和离子流密度[11],而被广泛采用.导线表面最大场强是通量线法计算合成电场和离子流密度的一个参数,对于分裂导线表面最大场强,通常有两种取值方法,分别是选取所有子导线表面最大场强的平均值和其中最大值作为分裂导线表面最大场强.而对于这两种不同取值方法下求解合成电场和离子流密度时带来的计算结果差异很少被讨论.
针对该现状,本文将一维黄金分割法(golden ratio,GR)扩展到二维,并对模拟电荷法进行优化,研究子导线内设置多个模拟电荷的情况.此优化模拟电荷法能够在保证较高计算精度的同时降低计算复杂度.应用该优化模拟电荷法(golden ratio charge simulation method,GRCSM)计算了分裂导线表面最大场强,并与COMSOL仿真结果进行比较,验证了GRCSM计算电场的准确性.此外,通过GRCSM计算了导线表面电场,采用“化曲为直”法绘制了电场线轨迹.在此基础上,基于通量线法对比分析了用分裂子导线表面最大场强的平均值和其中最大值求解合成电场和离子流密度的情况,并与文献[14]中的实测值进行了比较.研究结果有利于深入了解直流输电线路分裂导线表面电场、地面电场及离子流密度的分布特性,可为输电线路的设计及运维提供理论参考.
2 优化模拟电荷法
2.1 模拟电荷法
在导体内部设置若干个离散化的电荷(即模拟电荷),以大地为参考点,设置镜像电荷,然后根据导体电极表面的几何形状,在电极表面设置与模拟电荷数量相等的匹配点,建立如式(1)所示的模拟电荷线性代数方程组.
由式(1)可得到模拟电荷的电荷值,然后在导体电极表面选取校验点,校验点一般在两个匹配点之间选择.按式(2)计算校验点电位,当校验点电位满足所需精度时,即当模拟电荷在导体边界产生的电位满足给定的边界条件时,便可用其等效代替导体电极表面连续分布的电荷,并用这些电荷的解析公式来计算被求解场域内任一点的电场强度[15].

其中:φa,φb分别为第a个匹配点和第b个校验点的电位;Pan(Pbn)为第n个模拟电荷和镜像电荷在第a个匹配点(第b个校验点)上产生的电位,不同类型的模拟电荷计算式不同;Qn为第n个模拟电荷的电荷值(或电荷密度).
2.2 黄金分割法
黄金分割法在一维寻优问题的应用中效果较好且编程较为简单[16].其基本原理是给定最优解所在的寻优区间及收敛精度,根据式(3)–(4)选取区间内的两个初始试探点p1和p2.寻优过程中通过比较试探点的目标函数值来不断缩小搜索区间,并通过式(3)–(4)更新试探点,当搜索区间缩小到给定的收敛精度,则迭代结束[17].

其中a,b分别为寻优区间的下限和上限.
以计算如图1所示函数的极小值为例,说明搜索区间的收缩方法.
如图1(a)所示,若p1点函数值比p2点大,极小点必然在区间[p1,b],那么令p1=a,则产生了新的区间[a,b].同理,如图1(b)所示,若p2点函数值比p1点大,极小点必然在区间[a,p2],那么令p2=b,则产生了新的区间[a,b].到此区间缩短一次,然后再根据式(3)–(4)选择新的试探点,继续比较函数值来缩小寻优区间,直至区间缩小到给定的收敛精度ε,即b −a<ε时,极小值点为(b+a)/2.

图1 存在极小值的函数Fig.1 Function with minimum
2.3 模拟电荷优化设置
以如图2所示的±500 kV直流四分裂输电线路为计算模型,模拟电荷采用无限长直线电荷,研究子导线内设置多根模拟电荷的情况,导线参数如表1所示.
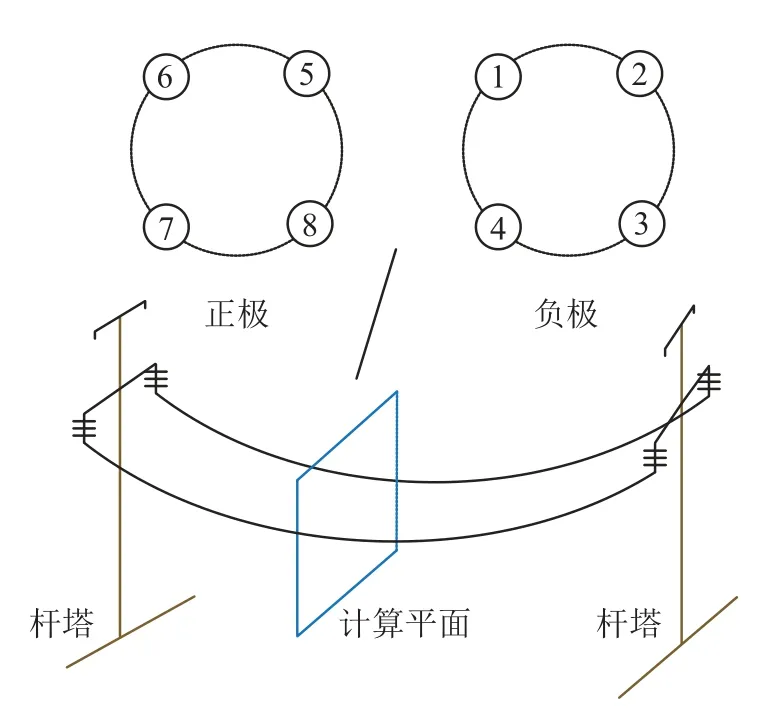
图2 输电线路计算平面Fig.2 Calculation plane of transmission line
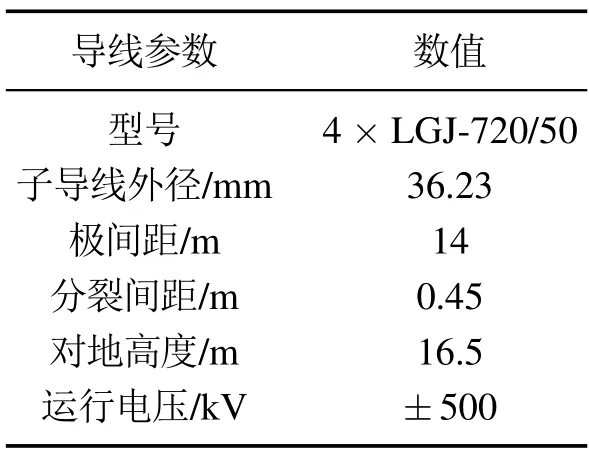
表1 导线参数Table 1 Wire parameters
当子导线内设置2根模拟电荷时,模拟电荷分别水平和垂直排列在子导线内的同心圆上.子导线内设置大于2根模拟电荷时,模拟电荷设置在子导线内同心圆的内接正多边形顶点处.以图3所示的子导线内设置3根模拟电荷为例,子导线半径为r,其同心圆半径为rs,模拟电荷设置在该同心圆内接正三角形的顶点处.匹配点对应于模拟电荷的位置设置在子导线表面,其数量与模拟电荷一致.校验点一般在匹配点之间设置,校验点的数量可以多于匹配点,鉴于本文需要比较校验点与匹配点的电位相对误差,故此在匹配点之间设置与其数量相等的校验点.

图3 子导线内模拟电荷分布示意图Fig.3 Schematic diagram of simulated charge distribution in sub conductor
由此可见,子导线内不同数量模拟电荷的最优分布可以转换为在子导线内部搜寻最优同心圆的问题,即若已知模拟电荷分布的最优同心圆半径,则可确定模拟电荷的分布.文献[7]和文献[9]均采用在子导线内同心圆周上设置模拟电荷的方法,最终目的都是搜寻模拟电荷分布的最优同心圆,不同的是前者采用经验公式法后者采用了遗传算法.经验公式法不能保证位置最优,且不适用于模拟电荷数量为2~5的情况.遗传算法搜索最优圆周的半径时因需设置诸多参数致使其复杂性较高,且参数设置的随机性易引起计算偏差.本文采用黄金分割法优化模拟电荷,既消除了经验公式法的局限性又无需设置任何参数,具体优化过程如下文所示.
GRCSM优化过程:
1) 模拟电荷数量初始值为2.
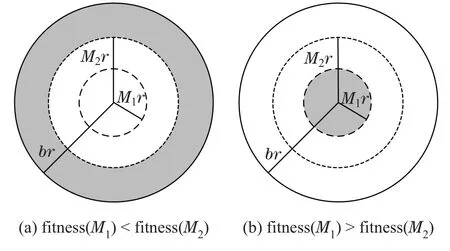
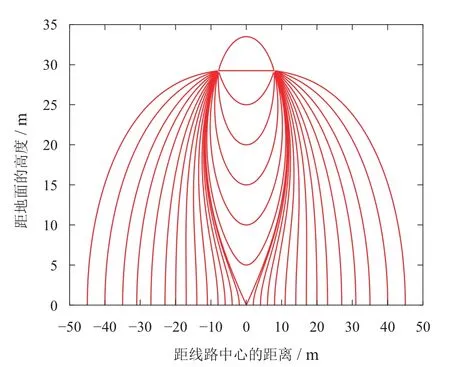
2) 定义M=rs/r(0 3) 按黄金分割原则确定两个初始M值:M1=b−0.618(b −a),M2=a+0.618(b −a),如此可确定如图4所示的半径分别为M1r和M2r两个初始同心圆,模拟电荷按前文所述原则分布在同心圆上. 4) 获取镜像电荷、匹配点和校验点的位置及匹配点电位列向量Vm,分别列写匹配点和校验点的电位系数矩阵Pm,Pc.按式(5)计算模拟线电荷密度列向量τ,然后按式(6)计算校验点电位列向量Vc[9]. 其中电位系数矩阵Pm和Pc中的元素Pij均采用下式进行计算: 其中:ε0为介电常数,F/m;xi,yi为子导线表面匹配点或校验点的横纵坐标;分别为第j根模拟电荷的横纵坐标、镜像电荷横纵坐标. 5) 以校验点与匹配点的电位平均相对误差构造目标函数[9]: 其中:n为校验点个数;Vci为通过模拟电荷法计算的第i个校验点电位,kV;Vmi为第i个匹配点电位,kV. 6) 比较模拟电荷分布在两个同心圆上时的目标函数值,若fitness(M1) 图4 黄金分割法确定的初始同心圆Fig.4 Initial concentric circles determined by golden ratio 7) 判断模拟电荷位置和精度是否满足要求,即模拟电荷位置不能过于靠近子导线中心,过于靠近子导线中心,容易引起电位系数矩阵“病态”,影响计算精度[7].同时,电位误差应以满足工程需要为前提,即电位误差应小于10−3[7],以本文±500 kV输电线路为例,由模拟电荷带来的电位误差应小于0.5 kV.若不满足则模拟电荷数量加1,回到步骤2)重新循环;若满足则优化结束. 获取满足要求的模拟电荷设置方法后,在每根子导线计算平面所在圆周每隔1◦取一个坐标点,然后在输电线路下的计算区域,以两极线中间为起始位置,在左右各50 m的范围内,每隔1 m取一个坐标点,按式(9)–(10)分别计算坐标点处的场强和电位[18]. 其中:n为模拟电荷数;x,y为子导线表面某点的坐标(或输电线路下计算区域内某点的坐标);xj,yj,和τj分别为第j根模拟电荷的横纵坐标、镜像电荷横纵坐标以及模拟电荷线密度. 空间中任一点B(x,y),按式(9)分别计算该点在x和y方向上的标称电场Ex和Ey,则描述电场线轨迹的微分方程为[19] B0(x0,y0)可设置为式(11)的初始条件,将B0点作为起始坐标,运用欧拉法或龙格库塔法求解微分方程,可得到沿电力线方向的一系列坐标点.通过公式(9)–(10)可求得这些坐标点的标称场强及电位值. 需要注意的是,当计算地面场强时,由于Ex为0,此时用欧拉法或龙格库塔法解式(11)的微分方程,将会出现结果不收敛的问题.为解决这一问题,本文采用“化曲为直”的方法计算电场线轨迹.图5为输电线路空间电场中任一条电场线. 图5 输电线路空间电场中任一条电场线Fig.5 Any electric field line in space electric field of transmission line 如图5所示,已知电场线上某点坐标为P(x,y),Q(x1,y1)为电场线上距离P点足够近的一点,采用“化曲为直”将PQ用直线代替,则Q点坐标可表示为 其中∆l为PQ两点的距离,即坐标点迭代步长,文中取0.01;d为方向系数,当PQ方向与电场线同向取1,反向取−1. 式(12)中的α可用P点合成场强E,x方向场强Ex和y方向场强Ey表示.即 在导线表面选择初始点P0,按式(12)–(13)确定下一个点P1的坐标,再以P1坐标和式(12)–(13)确定下一个点,如此迭代,直至电场线到达地面或另一极线的子导线时,则绘制结束. 基于Deutsch假设,合成电场与标称电场方向相同而幅值不同[11],以式(14)表示两者关系 其中:A为标量函数,E为标称场强. 离子流密度按式(15)计算 其中K为离子迁移率[20],本文K+取1.5×10−4m2/(V·s),K−取1.7×10−4m2/(V·s);ρ为计算点的电荷密度. 由式(14)可知,计算合成场强的关键是求解标量函数A,可采用式(16)计算[21]. 其中:Ae为导线表面A值;φi为计算点的电位;U为导线运行电压;ρe为导线表面电荷密度;η,φ为沿电场线的积分变量;ρm为通过计算点的电场线上的平均电荷密度. 由式(14)知,导线表面A值按下式计算: 其中:Emax为导线表面最大场强,文中分别取分裂子导线表面最大场强的平均值和其中最大值;Eon为导线起晕场强. 由Peek公式[22]可得正、负极线起晕场强计算公式 其中:m为导线表面粗糙系数,一般在0.4~0.6之间取值[23],文中m取0.5;r为导线等效半径,cm;δ为空气相对密度系数. 对于导线表面场强的边界条件,采用Kaptzov假设[24],即线路发生电晕后,其表面场强维持在起晕场强. 导线起晕电压 任一条电场线上所有点的平均电荷密度可表示为 ρe可通过式(21)迭代计算,当满足式(22)所给精度条件时迭代终止. 将ρe代入式(16)式可得计算点的A和ρ值.最后,根据式(14)和式(15)可得计算点的合成电场和离子流密度. GRCSM只需分割24次左右便可寻得最优解,优化结果如表2所示.由表2可知,各子导线中心设置1根模拟电荷时,校验点与匹配点的电位平均相对误差可高达0.38%,以本文±500 kV输电线路为例,此时由模拟电荷带来的电位误差高达1.9 kV,不能满足工程需要;子导线内设置2根水平和垂直排列的模拟电荷,寻优结果均为M取0.24时最佳,此时由模拟电荷带来的电位误差高达1.85 kV,同样不能满足工程需要;子导线内设置3根和4根模拟电荷时,虽然可以达到较高的计算精度,但寻优结果M都过小,即模拟电荷过于靠近子导线中心,容易使电位系数矩阵“病态”,此时可以认为模拟电荷越靠近子导线中心计算精度越高;子导线内设置5根模拟电荷,寻优结果M取0.039时最佳,校验点与匹配点电位平均相对误差约为0.0001%,此时由模拟电荷带来的电位误差仅为0.5 V. 表2 GRCSM优化结果Table 2 GRCSM optimization results 因此,GRCSM优化结果为子导线内设置5根模拟电荷,模拟电荷分布在子导线内的同心圆的内接正五边形的顶点处,如图6所示,其中同心圆半径rs取0.039r.由校验点与匹配点电位平均相对误差可知,此时已具备较高的计算精度,完全满足工程需要.另外,笔者计算发现继续增加模拟电荷数对计算精度的提高非常有限.由表2可知,当子导线内设置6个模拟电荷时,虽然计算精度进一步提高且收敛速度仍相当快,但此时由模拟电荷带来的电位误差较5个模拟电荷时仅降低0.1 V.值得注意的是,此时电位系数矩阵增加8阶,尽管这对GRCSM收敛时间影响不大,但会明显增加后续电场计算的复杂度,性价比较低. 图6 模拟电荷优化分布示意图Fig.6 Schematic diagram of optimized distribution of simulated charge GRCSM计算的所有校验点电位值以及电位标准值如图7所示.以匹配点电位(电位标准值)为基准,GRCSM计算的所有校验点的相对误差如图8所示. 图7表明,GRCSM计算的所有校验点电位误差均在2 V以内.图8表明,GRCSM计算的校验点的电位相对误差在0.00035%以内,平均相对误差约为0.0001%.由此可见,GRCSM的计算精度较高. 图7 校验点电位图Fig.7 Check point potential diagram 图8 校验点与匹配点电位相对误差图Fig.8 Diagram of relative error between check point and matching point potential 采用第2.3节所述计算模型,分别运用GRCSM和COMSOL软件计算分裂导线表面场强.其中,COMSOL中域内的材料参数如表3所示. 表3 材料参数Table 3 Material parameters COMSOL中关于无穷远边界的处理,文献[25]中对于有限元法计算输电线路离子流场中人工边界的选取中,建议双极性线路求解区域长和宽分别设定为(7~11)H(H为输电线路最低点对地距离)和(3.5~5.5)H.因此,本文选取长和宽分别为9 H和4 H的矩形求解域. COMSOL中网格的剖分选择用户控制网格,采用“自由剖分三角形网格”细化分裂导线区域的网格.其中整体网格和分裂导线网格如图9所示.计算模型中输电线路关于线路中心对称,忽略导线起晕后空间离子流场的分布,那么理论上两极线中心线上的电位为0.为检验COMSOL的计算误差,计算极线中心线上的电位,计算结果如图10所示. 图9 COMSOL网格的剖分图Fig.9 Sectional view of COMSOL grid 由图10可知,极线中心线上的最大电位误差为4.49 V,所有电位误差在−3.38~4.49 V之间,误差在允许范围内.因此,可以用COMSOL的电场计算结果来评估GRCSM计算电场的准确性.COMSOL和GRCSM计算的分裂导线表面场强如图11所示.由于正负极线的对称性,以负极线为例,两种计算方法的各子导线表面最大场强如表4所示. 图10 极线中心线上的电位计算结果Fig.10 Calculation results of potential on the center line of polar line 由图11可知,GRCSM和COMSOL计算的各子导线表面一周的场强吻合度较高.由表4可知,若以COMSOL计算结果为基准,GRCSM计算的子导线表面最大场强最大误差仅为0.03 kV/cm.由此可见,GRCSM计算电场具有较高准确性. 图11 不同计算方法的分裂导线表面一周场强线图Fig.11 Line diagram of one cycle field intensity on the surface of split conductor with different calculation methods 表4 不同计算方法的负极性子导线表面最大场强Table 4 Maximum field strength on the surface of negative electrode sub conductor with different calculation methods 综上可见,采用黄金分割法对模拟电荷法进行优化,无需像其他智能算法和有限元法一样进行过多的参数设置.GRCSM在保证较高计算精度的基础上,不仅降低了计算复杂性,同时减少了因参数设置的随机性而引起的计算偏差. 采用文中所述方法,对±500 kV江城直流输电线路导线表面电场和地面电场进行计算分析,其计算模型与第2.3节所述一致,仅线路参数不同.其中,江城直流输电线路导线参数如表5所示. 当采用表5所示导线参数时,GRCSM寻优结果为5个模拟电荷分布在半径为0.035r的子导线同心圆的正五边形上,这与采用文中第2.3节计算模型和表1导线参数的寻优结果相差不大.计算表明,分裂间距、子导线外径和分裂数对寻优结果影响较大,而极间距、导线对地高度、运行电压对寻优结果影响很小.由此可见,由于表5导线参数中分裂间距的微小变化,才导致寻优结果略微不同.此外,对于不同的导线参数,GRCSM的优化结果不同,即GRCSM能够随导线参数的变化灵活调整模拟电荷的数量及位置.相比于±500 kV直流输电线路,±800 kV直流输电线路通常采用六分裂导线,而更高等级的±1100 kV直流输电线路通常采用八分裂导线,电压等级的改变对于计算的影响仅体现在导线位置和参数发生变化.对于同塔双回直流输电线路和交流输电线路,同样可以采用本文方法确定模拟电荷位置,但是在电场求解时前者要考虑导线排列方式的影响,后者不仅要考虑导线排列方式的影响,还要考虑相序的影响.因此,本文方法也适用于不同电压等级的输电线路电场的求解. 表5 导线参数Table 5 Wire parameters 各子导线表面电场的计算结果如图12所示.由于极线间距远大于子导线半径,为增强图像的可观性,图12(a)和(b)分别展示了正负极线的子导线表面二维电场分布情况. 图12 子导线表面电场的计算结果Fig.12 Calculation results of electric field on the surface of sub conductor 由图12可知,正负极线的子导线表面电场分布关于线路中心对称.受其他子导线和大地的共同作用,各子导线表面场强分布很不均匀,最高与最低场强之差可达5 kV/cm;对比发现,同一水平线上的子导线最大场强随着与线路中心距离减小而明显增强;同一垂直线上的子导线最大场强随着与地面距离减小而略有增强.此外,每根子导线的最大表面电场均出现于背向4根子导线中心的位置,最小表面电场均出现于面向4根子导线中心的位置. 图13所示为电场线轨迹图,图14和图15所示为地面标称电场、合成电场及离子流密度的计算值以及文献[14]中对江城直流合成电场、离子流密度的实测值. 图13 电场线轨迹Fig.13 Electric field line trajectory 图14 标称电场和合成电场横向分布Fig.14 Transverse distribution of nominal electric field and synthetic electric field 图15 离子流密度横向分布Fig.15 Transverse distribution of ion current density 由图13可知,采用“化曲为直”法可以完整画出电力线轨迹.此法无需求解微分方程,也就避免了地面电场水平分量为0时微分方程结果不收敛的问题. 由图14–15可知,合成电场和离子流密度实测值与计算值相比分散性较高,这是由于Deutsch假设不考虑风的影响,且带电离子沿电场线轨迹运动.而实际中在风的作用下,带电离子的运动轨迹可能会偏离电场线,即离子流场会发生变化,从而使合成电场发生变化.采用分裂子导线表面最大场强的平均值与其中最大值计算得到的地面合成电场的最大值分别为7.25 kV/m(正极)、−8.64 kV/m(负极)和8.04(正极)、−9.65 kV/m(负极),相差14.04%和11.69%;所得的离子流密度最大值分别为1.80 nA/m2(正极)、−2.12 nA/m2(负极)和2.43 nA/m2(正极)、−2.80 nA/m2(负极),相差35%和32.08%. 对比图14–15中合成电场和离子流密度的计算值与实测值可知,采用分裂子导线表面最大场强所得两个参量的计算结果与实测值的吻合度明显高于采用最大值.因此,采用分裂子导线表面最大场强的平均值计算的地面合成电场和离子流密度比用其中最大值计算的更符合实际.同样也表明,在不考虑风速的影响时,基于Deutsch假设的通量线法可以基本反映输电线路合成电场和离子流密度的实际情况. 本文将一维黄金分割法扩展到二维,对模拟电荷法进行了优化,并计算了输电线路分裂子导线表面电场、合成电场和离子流密度,得出以下结论: 1) 黄金分割优化模拟电荷法实现过程简单且具有较高的计算精度,可随导线参数的变化灵活调整模拟电荷的数量及位置.此方法同样适用于导线分裂数更多的特高压直流输电线路电场的求解; 2) 采用“化曲为直”法绘制电场线轨迹,不必求解微分方程,从而避免了微分方程因地面电场水平分量为0而结果不收敛的问题; 3) 用黄金分割优化模拟电荷法计算每根子导线表面最大场强,分别取其平均值与其中最大值计算地面合成电场和离子流密度.结果表明,前者计算的地面合成电场和离子流密度与实测值更吻合.


2.4 电场强度和电位

2.5 电场线轨迹方程




2.6 合成电场和离子流密度




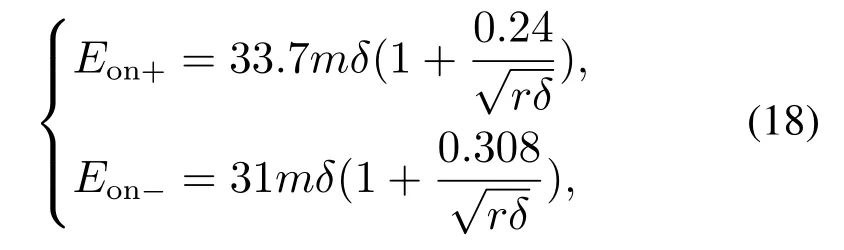



3 计算结果比较
3.1 优化结果


3.2 电位比较
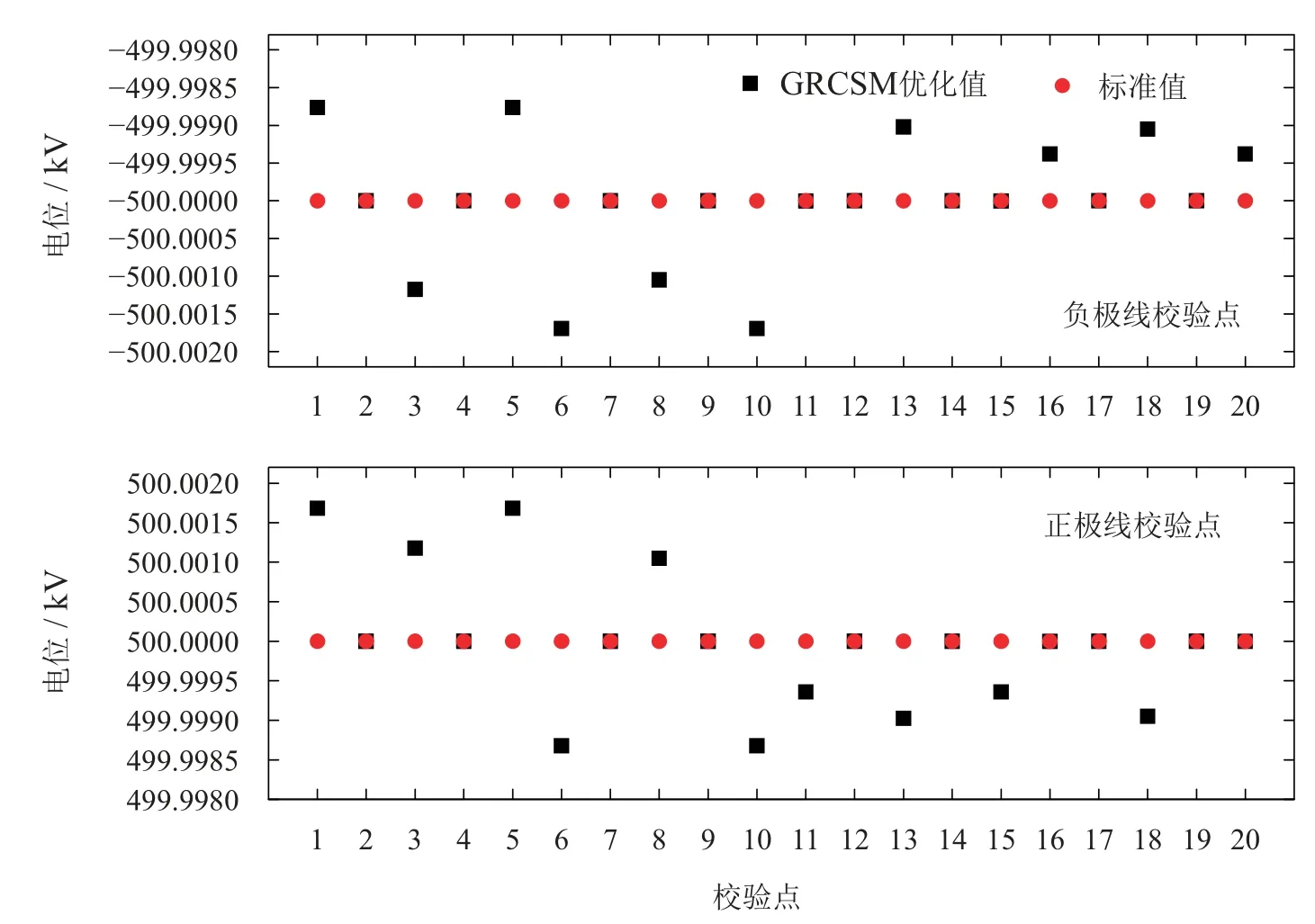
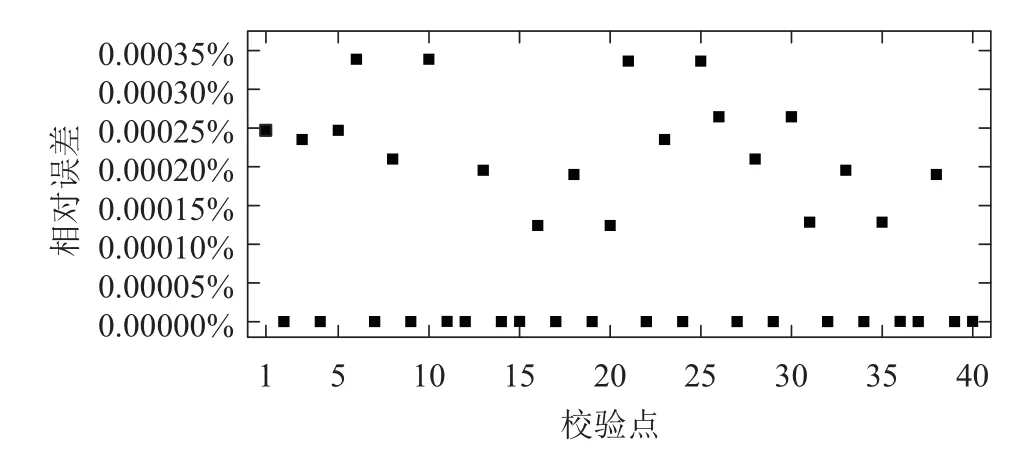
3.3 电场比较



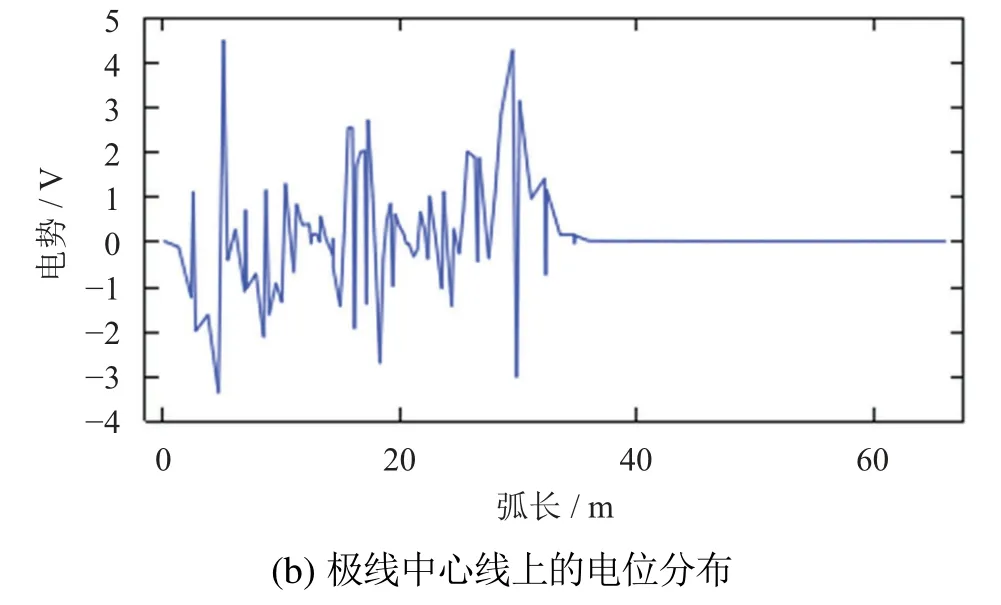


4 计算与分析
4.1 计算参数说明

4.2 导线表面电场的计算
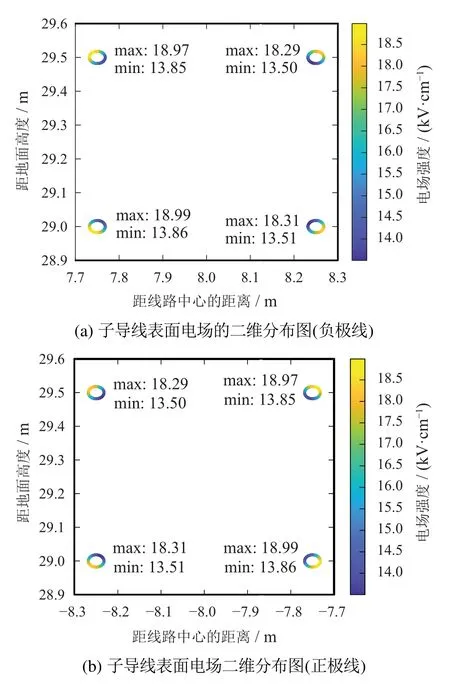
4.3 地面电场及离子流密度计算


5 结论

