基于模型试验的预裂孔爆破参数优选
李祥龙,杨长辉,王建国,王子琛,胡启文
(1. 昆明理工大学国土资源工程学院,云南 昆明 650093;2. 云南省中-德蓝色矿山与特殊地下空间开发利用重点实验室,云南 昆明 650093;3. 中煤科工集团西安研究院有限公司,陕西 西安 710077;4. 北京理工大学机电学院,北京 100081)
近年来,随着社会对爆破安全的要求越来越严苛,受地质条件、工程条件和技术条件等限制,为了降低爆破对周边岩体的振动破坏,保障周边岩体和建筑的安全性,在施工中广泛采用预裂爆破技术。研究预裂孔参数对预裂爆破技术应用具有重要意义[1–3]。邓珂等[4]利用数值模拟软件LS-DYNA,对初始地应力对预裂缝成缝的影响进行了研究。朱强等[5]通过数值模方法研究了空气间隔装药预裂爆破对岩体的损伤影响,提出采用径向不耦合药卷和反向起爆可以优化空气间隔装药预裂爆破效果。He 等[6]应用数值模拟软件LS-DYNA 优化了预裂爆破模型,并将其应用于现场,使有效半孔率超过20%,减振率达28.2%。杨仁树等[7]基于数字激光动态焦散线,研究了预裂缝对爆生裂纹和原生裂纹动态断裂特性的影响。璩世杰等[8]进行了不同角度的节理对预裂爆破效果的试验,得到了不同角度下预裂缝成缝效果。陈俊桦等[9]结合岩石爆破理论、爆生气体和应力波共同作用等理论,提出了基于岩石损伤的预裂爆破参数计算公式。Ma 等[10]对预裂爆破的成缝机理进行了探讨,得到了预裂孔孔距的计算公式,并验证了预裂缝的减振效果。饶宇等[11]通过分析预裂孔爆破和主爆破的功率谱和能量谱,得出预裂孔爆破形成的预裂缝能很好地阻挡主爆破能量的传播,揭示了预裂缝对爆破振动传播及其频谱特征变化的影响。严鹏等[12]通过对爆破开挖振动监测和爆破损伤的声波监测,得到了预裂爆破的振动衰减规律。Xiao 等[13]结合爆炸力学,揭示了预裂爆破的开裂机理,提出了一套预裂爆破参数设计公式,最终确定了黑岱沟的预裂爆破参数。
以往学者主要通过数值模拟、室内实验及理论推导等手段对预裂爆破的影响因素开展了研究,然而针对预裂孔参数的模型试验研究却较少。本研究拟采用相似材料模拟预裂孔爆破过程,通过正交分析确定爆破成缝效果最佳的预裂孔爆破参数。
1 试验准备与设计
(1) 模型的制备。本试验的相似模拟对象为云南某露天矿山,现场岩体主要为片岩、大理岩体、矽卡岩。根据相似理论,选用C30 混凝土作为相似材料,其水、水泥、砂、石子的配合比为0.60∶1.00∶2.51∶3.93,平均密度为2.382 g/cm3,抗压强度为27.6 MPa,弹性模量为27.6 GPa。一共浇筑16 组模型,通过插入钢筋预制炮孔,如图1所示。为了增加约束,爆破时不脱模。

图1 预制预裂孔的混凝土模型Fig. 1 Model of concrete with precast presplitting hole
(2) 不耦合系数(因素A)水平。徐颖等[14]的模型试验研究表明,当不耦合系数为1.67 时,爆炸裂纹数和裂纹扩展长度最佳,为此选用1.33、1.67、2.00 和3.00 这4 个水平,分别对应A1、A2、A3、A4。
(3) 延期时间(因素B)水平。何理等[15]通过浇筑混凝土模型模拟预裂爆破实验,确定孔间最佳延期时间为11~15 ms,司剑峰等[16]通过模型研究得出最佳延期时间约为8 ms,因此本研究中延期时间选用8、10、12、15 ms 4 个水平,分别对应B1、B2、B3、B4。
(4) 最大单响药量(因素C)水平。本次模型试验选用数码电子雷管,导爆索为主爆药,模型试验的线装药密度为2 g/m,孔深为80 cm,因此单孔装药量为1.6 g,选用1.6、3.6、5.4 g,分别对应C1、C2、C3。考虑到因素C只有3 个水平,为此采用拟水平设计将因素C补充至4 个水平,用3.6*表示为因素C的拟最大单响药量3.6 g 水平,即C4。孔距统一为90 mm,填塞长度为1.2 倍孔径。考虑误差而增设误差项(D),对试验没有影响。正交试验因素水平见表1。

表1 正交试验因素水平Table 1 Factors and levels for orthogonal tests

2 正交试验分析
本试验设有3 个因素,每个因素均设计了4 种水平。需采用4 因素4 水平的正交表L16(44),共计有16 组试验,不同因素组合试验的正交表见表2。
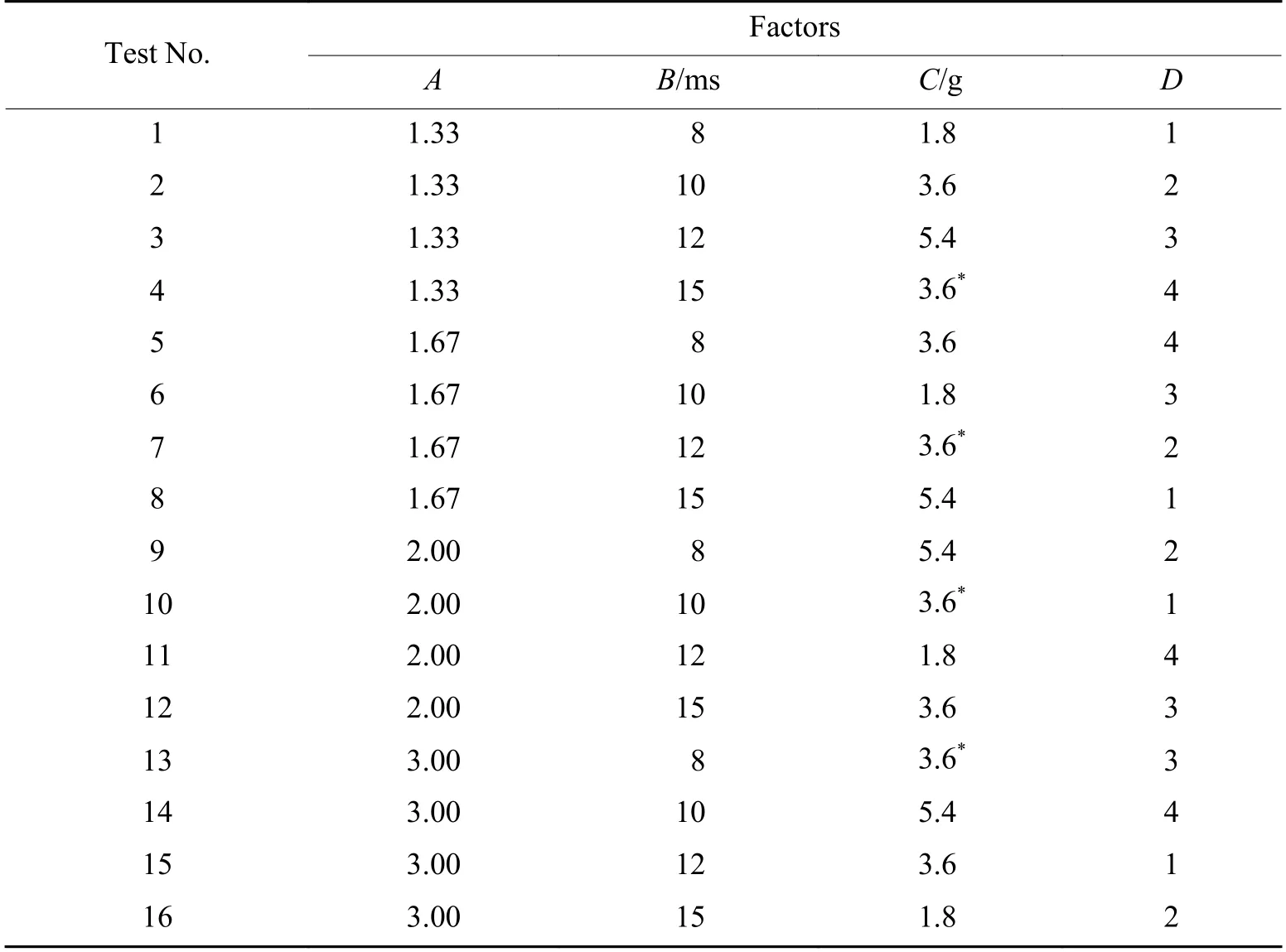
表2 相似材料模拟试验的正交设计Table 2 Orthogonal test design of the simulation tests with similar material
根据设计的16 组方案进行相似模型试验,有效半孔率、预裂缝宽度和原岩损伤率的测试过程如图2、图3 和图4 所示,具体的试验结果列于表3。
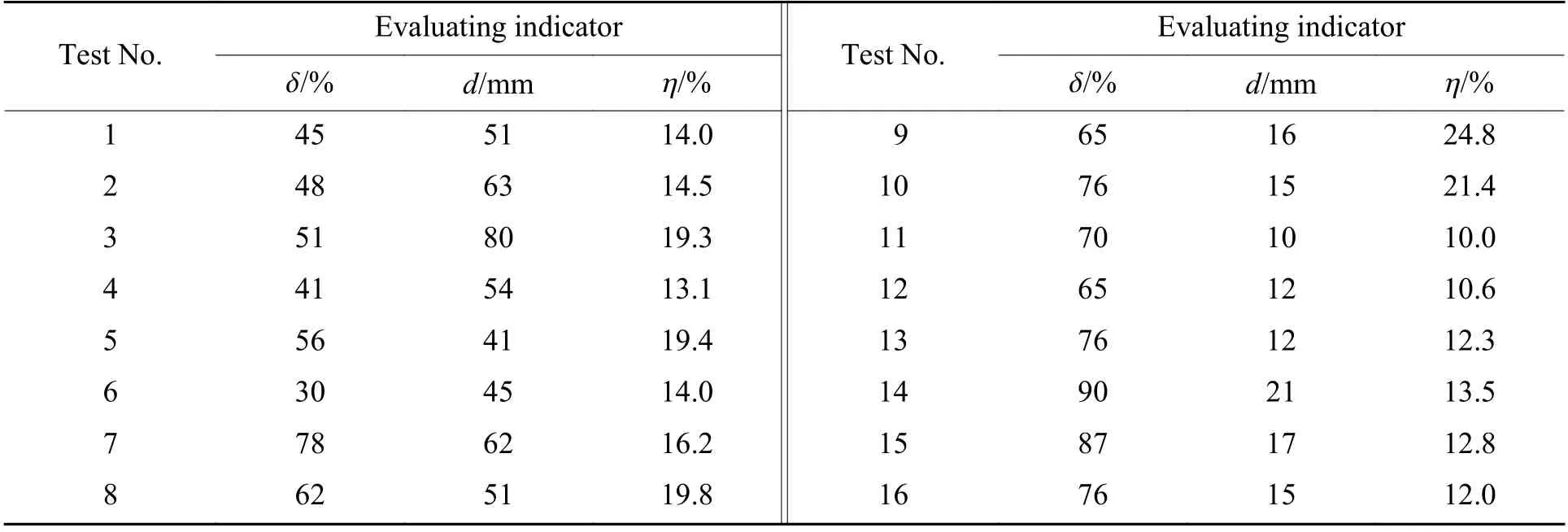
表3 爆破效果统计Table 3 Statistics of blasting effect

图2 有效半孔率的测量Fig. 2 Measurement of effective half-porosity

图3 预裂缝宽度的测量Fig. 3 Measurement of pre-crack width

图4 爆破声波测试仪器Fig. 4 Instrument of blasting acoustic test
2.1 极差分析
Ki为该列因素的第i个水平所对应分析的评价指标数值之和。ki为该列因素Ki具有的水平数的均值。极差R为该列k1、k2、k3、k4中的最大值减去最小值。极差越大,则该因素对应的评价指标的影响越显著。
根据16 组试验的试验结果,对有效半孔率、预裂缝宽度和原岩损伤率下的各因素进行极差分析,见表4。由表4 可知,当只考虑有效半孔率时,因素A的ki指标有k1 表4 极差分析Table 4 Range analysis 对比分析极差可知影响预裂爆破效果的各个因素的主次关系。对于有效半孔率,因素A的极差最大,说明不耦合系数对预裂爆破效果中有效半孔率的影响程度最大,因素B、因素C依次减小,各个因素的影响程度为:不耦合系数的影响最大,延期时间次之,最大单响药量的影响最小。对于预裂缝宽度,因素A的极差最大,说明不耦合系数对预裂爆破效果中预裂缝宽度的影响程度最大,因素B、因素C依次减小,各个因素的影响程度为:不耦合系数的影响最大,延期时间次之,最大单响药量的影响最小。对于原岩损伤程度,因素C的极差最大,说明最大单响药量对预裂爆破效果中原岩损伤程度的影响程度最大,因素A、因素B依次减小,各个因素的影响程度为:最大单响药量的影响最大,不耦合系数次之,延期时间的影响最小。 方差分析是考察各因子在各水平下的效益有无显著差异的一种分析方法,与极差分析相互验证补充。在方差分析中偏差平方和QT的表达式为 通过计算得出F后,与选定置信度 α的F分布中的定值进行比较,当F>Fα时,该因素对该评价指标影响显著。 根据分析得到统计结果,如表5 所示。最大单响药量仅有3 个水平,故计算时自由度为2。 查询F分布表可知,F0.10(2, 3) = 5.46,F0.05(2, 3) = 9.55,F0.01(2, 3) = 30.82,F0.10(3, 3) = 5.39,F0.05(3, 3) =9.28,F0.01(3, 3) = 29.46。 根据表5,对于预裂缝宽度,因素A的F>F0.01(3, 3),对于有效半孔率,因素A的F>F0.05(3, 3),与极差分析结果基本一致。其他两个因素虽然没有达到显著水平,但是总体上仍反映并证明了极差分析结果。 表5 方差分析结果Table 5 Results of variance analysis 对于有效半孔率和原岩损伤程度,3 个因素不显著的原因是本试验的误差相对较大,而且误差的自由度相对较小,使得检验的灵敏度较低。 (1) 因素A在有效半孔率指标和预裂缝宽度中的影响程度排第1,为最重要因素;在对原岩的损伤程度指标中排第2,在方差分析中,因素A在预裂缝宽度情况下F>F0.01(3, 3),因素A在预裂宽度情况下达到显著水平,故可取A1水平,即1.33。 (2) 因素B在有效半孔率指标和预裂缝宽度中的影响程度排第2,为次要因素;在对原岩的损伤程度指标中排第3,为最不重要因素;故可取水平B2和水平B3,因为在因素B取B2时,3 种指标总值分别为244、144、63.4,比B3时的286、169、58.6 指标差,故取B3水平,即12 ms。 (3) 因素C在有效半孔率指标和预裂缝宽度中影响程度排第3,为最不重要因素;在对原岩的损伤程度指标中排第1,为最重要因素,故应取C1水平,即1.8 g。 通过C30 混凝土相似材料的爆破模型试验,对影响预裂孔爆破成缝效果的多因素进行了正交试验分析,得到以下结论。 (1) 方差分析表明,预裂缝宽度对不耦合系数最敏感,且不耦合系数越大,预裂缝宽度越小;有效半孔率与不耦合系数成正比,说明在药量一定的情况下,增大不耦合系数可提高对炮孔壁的保护。 (2) 延期时间对有效半孔率和预裂缝宽度的影响程度均排第2,说明延期时间对爆破成缝和孔壁的保护均有影响,因此选择合理的延期时间对爆破效果至关重要。 (3) 模型试验爆破效果评价表明,不耦合系数取1.33、延期时间取12 ms、最大单响药量取1.8 g 的因素组合条件下,预裂爆破成缝和减振效果最优。
2.2 方差分析

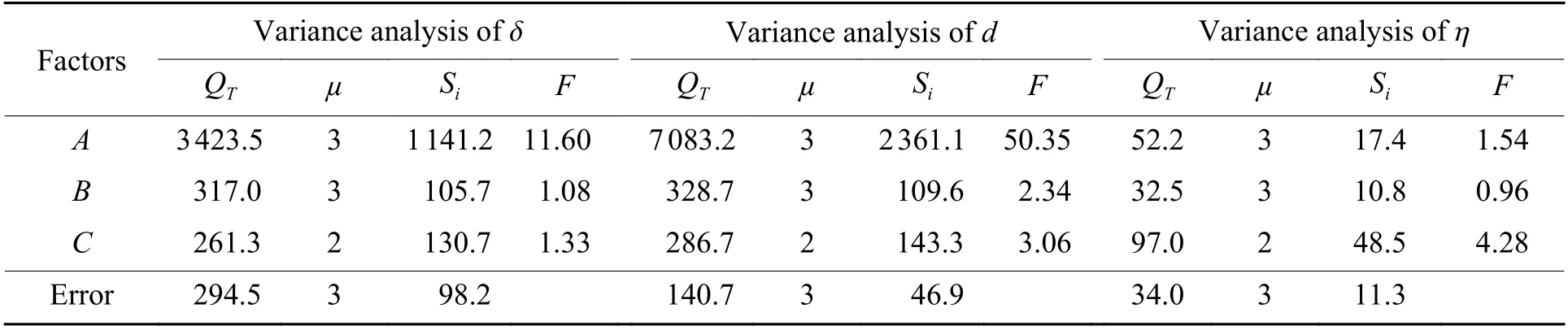
2.3 最优水平确定
3 结 论

