多次水下爆炸中船体梁的累积毁伤效应

唐正鹏，李翔宇，郑 监

（国防科技大学文理学院, 湖南 长沙 410073）

水下爆炸对舰船的毁伤主要是利用水下爆炸产生的冲击波和爆轰产物形成的气泡脉动对目标进行毁伤[1–2]。随着目标防护能力的不断增强[3]，单次水下爆炸已经不足以对大型舰船目标造成致命性毁伤效果，为此需要对大型舰船目标进行多次打击，利用多次水下爆炸对舰船的累积毁伤效应，达到对舰船的致命性毁伤。

目前，国内外对于多次水下爆炸对舰船目标的累积毁伤研究较少。张斐等[4]对多次水下爆炸作用下钢板的动态响应进行了试验和数值模拟，得到钢板的塑性变形历程规律。李海涛等[5]进行了水下爆炸作用下对称结构船体梁整体毁伤特性试验，结果表明，在一定爆炸范围内，炸药远距离多次爆炸比近距离一次爆炸造成的梁结构中垂损伤变形更大。Rajendran 等[6]根据板架结构在冲击载荷下的变形，以冲击因子为依据对结构变形特征进行分类，并通过大量分析得出其变形规律。Jiang 等[7]利用声学方法，对结构湿表面进行耦合作用处理，以并列梁代替板架结构，计算了爆炸冲击载荷作用下板架结构的响应。Menkes 等[8]通过实验手段得出了冲击载荷作用下金属梁结构的3 种典型失效特征。

在数值模拟方面，张馨等[9]基于LS-DYNA 软件，研究了冲击波作用下板架结构的破坏特征。张阿漫[10]采用ABAQUS 软件模拟了近场爆炸气泡与舰船边界的耦合作用，发现气泡收缩过程中舰船整体发生了毁伤。Yuen 等[11]和Langdon 等[12]考虑了温度对结构应变率的影响，基于ABAQUS 软件对比各种结构形式板架在冲击波作用下的响应，总结了各种板架结构的变形特征。

多次水下爆炸结构累积毁伤方面的研究多集中于固支板或焊接结构的累积毁伤效应，而对于以船体梁为目标的累积毁伤研究较少。He 等[13]进行了反复冲击下梁动态特性的试验研究，从而对船只与浮冰多次碰撞的损伤进行评估。本研究将针对多次水下爆炸下船体梁的累积毁伤效应，通过对船体梁的动态响应进行数值模拟和试验研究，获得多次爆炸下船体梁的累积毁伤特性，以期为反复冲击下舰船的毁伤研究提供参考。

1 多次水下爆炸下船体梁的动态响应试验

1.1 试验装置及设计

对船体梁在水下爆炸作用下的动态响应进行试验研究，试验布局如图1 所示，主要包括小型水箱、高速摄影机、光源、船体梁、炸药、测试装置等。通过高速摄影记录整个水下爆炸过程，以及水中气泡与结构的相互作用过程。水箱为长方体，尺寸为2 m×2 m×3 m（长×宽×高），注入水深1.5 m。船体梁材料为Q345 普通钢，尺寸为750.0 mm×97.5 mm×50.0 mm（长×宽×高），横板、侧壁、底板厚度均为1.5 mm，中间采用4 个横板将其分为5 个舱室，船体梁的上表面呈开口状，四周用绳子卡住，保证在不受力的时候船体在水中静止。船体梁自由漂浮时的吃水深度为30 mm。图2 为试验所用的黑索金（RDX）药柱，装药量分别为2.95、2.96、3.00 g，用装药量为0.60 g TNT 当量的雷管在药柱端部起爆，因雷管当量较小，且在药柱端部起爆，因而可以忽略其影响。3 次爆距分别为300、200 和100 mm，试验工况如表1 所示。表1 中，W为药柱质量，H为爆距。

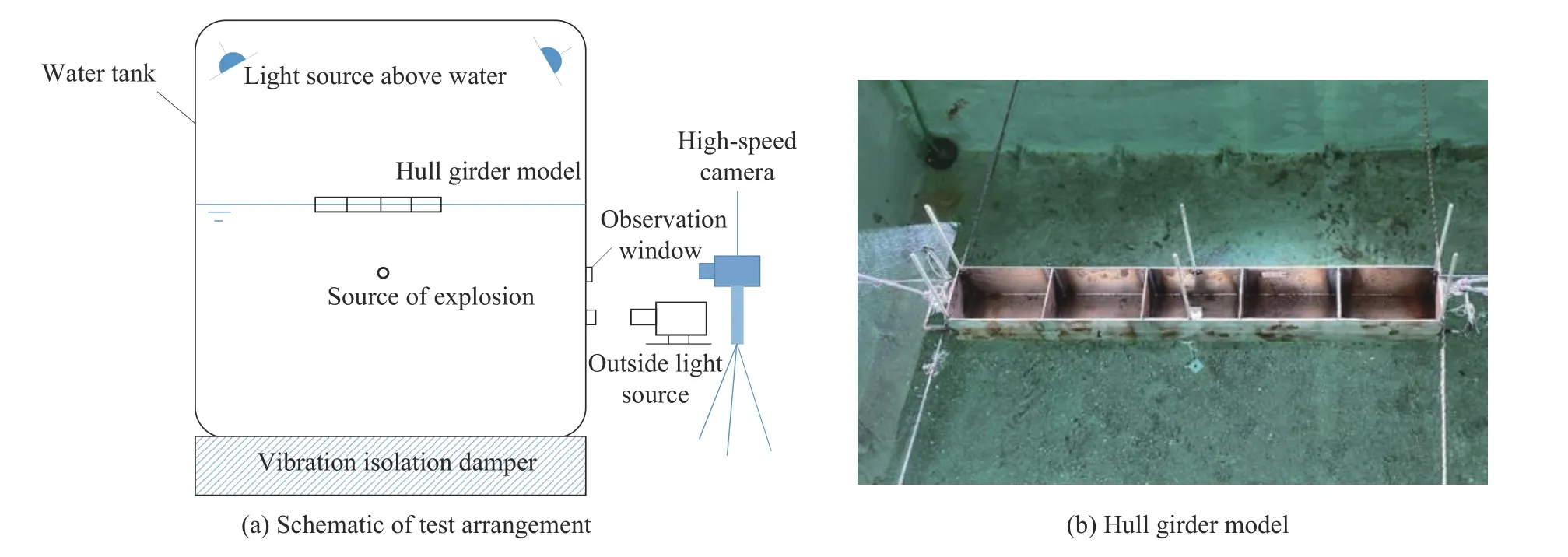
图1 试验布局和船体梁模型Fig. 1 Test arrangement and hull girder model

图2 黑索金药柱Fig. 2 RDX cylindrical explosive charge

表1 试验工况Table 1 Test conditions

1.2 试验现象

利用高速摄影记录整个水下爆炸过程，如图3 所示。零时刻，起爆瞬间产生火光，高速摄影开始记录。观察照片发现，起爆后0.2 ms，船体梁周围水体发生波动。假设冲击波在水中的传播速度为水中声速，起爆点距离船体梁300 mm，计算出冲击波到达时刻为0.2 ms，说明该时刻爆炸产生的冲击波已到达船体模型，并作用于船体梁上。16.6 ms 为第1 次气泡脉动半径最大时刻，根据库尔最大半径估算公式[14]计算出气泡最大半径为220 mm，起始爆心距离船底300 mm。气泡半径最大时，未接触到船底。37.0 ms左右，气泡收缩到最小，此时为第1 次脉动周期，与估算公式计算出的42.0 ms 气泡脉动周期值相差11.90%。

图3 水中气泡脉动过程Fig. 3 Underwater bubble pulsation process

1.3 船体梁变形结果

第1 次水下爆炸结束后，船体梁局部与整体都未发生塑性变形。通过高速摄影观察，发现爆炸产生的气泡未与船体梁底部接触，第1 次爆炸气泡半径小于爆距，爆炸产生的能量使船体梁做向上的刚体运动，刚体运动吸收了爆炸能量，使得水下爆炸产生的弯矩变小，船体梁整体未发生塑性变形。如图4所示，第2 次水下爆炸后，产生的气泡半径与爆距大致相等，在冲击波的作用下，船体梁整体向上做刚体运动，但未发生弯曲塑性变形，仅有船底中部板块发生轻微变形，中部底板向舱内凹陷。

图4 第2 次水下爆炸后船体梁底部Fig. 4 Bottom of hull girder after the second underwater explosion

第3 次爆炸试验的变形情况以及利用三维激光扫描仪设备获得的中部剖面如图5 所示。船体梁整体发生中拱塑性弯曲大变形，中部底板向舱内凹陷，且凹陷程度大于第2 次凹陷。中部圆孔为加速度测试器螺栓固定圆孔，因爆炸使其脱落，未测出船体梁中部的加速度时程曲线。第3 次水下爆炸产生气泡的半径约为爆距的2 倍，起爆后在水中产生冲击波，冲击波到达船体梁中部使中部底板向舱内凹陷。水中冲击波载荷由中间向船体梁两端逐渐扩展，当爆距较小时，前期产生的较大水下载荷作用于船体梁中部形成弯矩，船体梁整体发生中拱弯曲大变形。

图5 第3 次水下爆炸后船体梁变形Fig. 5 Deformation of hull girder after the third underwater explosion

2 数值模拟方法

2.1 计算工况

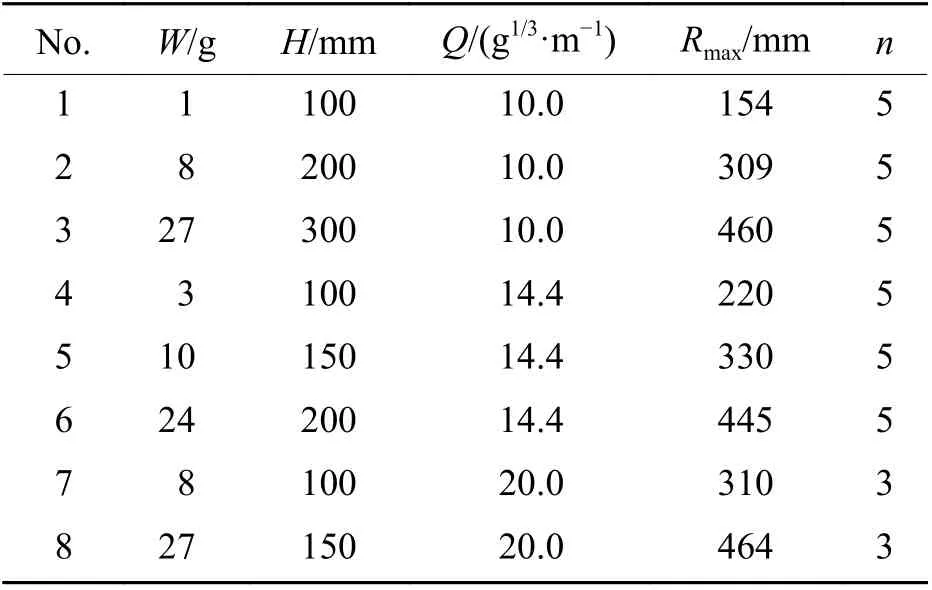
表2 各工况计算参数Table 2 Parameters in different calculation cases

2.2 一维映射模型

由于炸药与船体梁结构之间有一段距离，与整个流场相比，炸药尺寸很小，炸药爆轰、能量释放阶段的作用水域也不大，如果在一个计算模型中同时考虑炸药能量释放、冲击波传播、气泡脉动、结构响应，则计算模型的单元数量会非常庞大。为了解决时间和空间上的矛盾，可以在炸药爆轰阶段忽略重力和水深变化的影响。采用一维轴对称模型，也就是牺牲空间计算精度换取时间计算精度，网格划分可以非常细密，以捕捉早期高频冲击波。冲击波波阵面传播一段距离后，将一维模型计算结果映射到增加了考虑结构的三维模型里进行流固耦合分析，计算流体域可以包含结构附近的部分流体，并在边界处施加压力流出边界条件以模拟无限水域。采用这种方法可减少计算耗费，提高计算精度。

首先进行一维模型计算，材料选择RDX 和水，其中RDX 采用JWL 状态方程描述，水采用 Shock 状态方程描述，强度模型为 Hydro[4]。新建二维欧拉计算区域，建立半径为200 mm 的楔形水域，根据RDX 的质量密度换算出对应半径，填充在顶部，并在顶端设置起爆点，设置求解总时间为0.2 ms，一维计算结果如图6 所示。观察压力云图发现，当冲击波端部即将到达结构的距离时暂停计算，并保留一维计算结果生成映射文件。

图6 一维楔形模型的压力云图Fig. 6 Pressure nephogram of one-dimensional wedge model

2.3 三维有限元计算模型

利用AUTODYN 新建一个三维欧拉多物质耦合求解域，场域长800 mm，宽140 mm，高300 mm。为了方便计算，采用边长为5 mm 的正方体网格。在0～240 mm 高度范围内填充水域，在240～300 mm高度范围内填充空气域，再在水域中央挖出一个深30 mm、长750 mm、宽100 mm 的长方体填充空气，模拟放置船体梁浸水部分，并在场域边界添加流出条件。用三维Shell 单元建立船体梁模型，选择材料为Q345 钢。主要参数：弹性模量为206 GPa，泊松比为0.3，屈服强度为345 MPa，密度为7.85×103kg/m3。采用考虑应变率效应的 J-C 本构模型[4]，船体梁模型如图7 所示，模型尺寸为750 mm×100 mm×50 mm，网格大小为5 mm×5 mm，横板数量为6，各板厚度均为1.5 mm。数值模拟涉及了船体梁、空气、水等多物质耦合，选择AUTODYN 自带的流固耦合计算。通过计算发现，爆炸8 ms 船体梁塑性变形后，整体弯曲变形进入振荡阶段，故计算停止时间设置为8 ms。

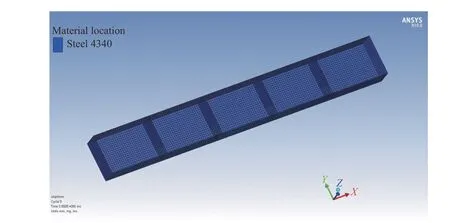
图7 船体梁有限元模型Fig. 7 Finite element model of hull girder

2.4 多次水下爆炸加载方法

采用AUTODYN 模拟多次水下爆炸加载下船体梁动态响应的核心是将上一次船体梁的数值模拟结果作为下一次数值模拟的初始条件。实际试验过程中，多次水下爆炸之间具有一定的时间间隔，第2 次水下爆炸载荷加载时水域基本恢复到初始状态。因此，在数值模拟时将第1 次的Euler 域（水和空气）删除，重新建立同样的初始水域和空气域，调整船体梁模型与Euler 域位置，将一维模型的模拟结果映射加载到水域中，最后设置Euler 与Lagrange 区域的耦合及计算时间。图8 显示了在爆距为100 mm、炸药量为3 g 工况下，船体梁第3 次水下爆炸加载时的有限元模型。为方便观察，隐藏了空气域，Euler域的边界条件设置为流出边界条件。

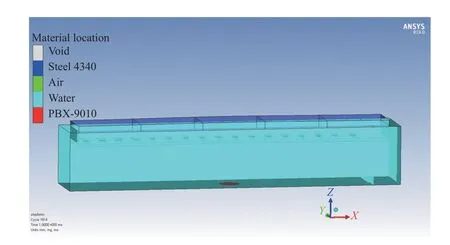
图8 100 mm 爆距有限元计算模型Fig. 8 Finite element model for the calculation case with 100 mm stand-off distance

3 试验与模拟结果的对比分析

3.1 船体梁变形模式及变形量

将图9 与图4、图5 中数值模拟与试验结果对比可以看出，船体梁的整体与局部变形模式和程度基本吻合。对同一船体梁进行了3 次不同爆距的水下爆炸加载数值模拟。工况1 中，爆距为300 mm，水下爆炸加载后船体梁模型整体和局部未发生形变；如图9(a)所示，工况2 中，爆距为200 mm，水下爆炸加载后，船体梁模型中部舱段底板向内凹陷，两端舱段底板向外轻微凸起，整体未发生明显弯曲变形；如图9(b)、图9(c)所示，工况3 中，爆距为100 mm，水下爆炸加载后，船体梁整体发生中拱弯曲大变形，中部底板向舱内凹陷，且其凹陷程度明显大于第2 次凹陷。

图9 船体梁变形数值模拟结果Fig. 9 Numerical simulation results of hull girder deformation

工况2 和工况3 的最大中拱变形挠度分别为11.00 和44.00 mm，随着爆距缩短，船体梁的累积变形呈非线性大幅度增长，且中部底板的局部变形程度远大于其他底板。水下爆炸试验与数值模拟得到的船体梁底部中线上3 次累积后变形挠度如图10 所示，将横坐标原点选在梁中点，变形挠度为底板X轴（长度）方向中线在Z轴（高度）方向的形变位移。试验测量和数值模拟得到的变形挠度最大值分别为42.98 和44.00 mm，中间底板的最大挠度分别为16.25 和15.00 mm，数值模拟比试验测量的整体变形最大挠度大2.37%，局部变形最大挠度小7.69%。数值模拟与水下多次爆炸试验测得船体梁塑性变形程度与模式是相近的，表明本研究中的数值模拟模型及方法可以有效地模拟多次水下爆炸加载后船体梁的累积变形特性。

图10 船体梁变形的试验与数值模拟结果对比Fig. 10 Comparison of deformation of hull girder between test and simulation results

3.2 船体梁累积毁伤变形分析

工况1～工况8 的数值模拟结果如图11所示。可以看出，船体梁的最终塑性变形挠度与爆炸载荷作用于船底的冲击因子Q有关，Q值越大，船体梁的塑性弯曲变形程度越大。当Q=10.0 时，船体梁仅发生局部变形，连续多次水下爆炸加载对船体梁变形没有产生累积效果；当Q>10.0 时，在Q相同的情况下（即峰值压力相等），随着装药量增大，船体梁的挠度也随之增大，这是因为当水下爆炸载荷超压相等时，装药量越大，则比冲量越大，水下爆炸载荷作用于船体梁的时间越长，从而使得船体梁产生更大的塑性弯曲变形；当Q增大至20.0 时，船体梁整体发生严重的中拱塑性变形并破损，无法再进行多次水下爆炸加载。当Q= 14.4 时，在多次水下加载过程中，船体梁的累积效果明显，且挠度呈线性不断增大。随着装药量增加，船体梁的挠度也随之增大，挠度D与爆炸加载次数n近似满足

图11 多次爆炸加载后累积挠度值Fig. 11 Cumulative deflection values after multiple explosive loading

数值模拟工况4 中，装药量为3 g，爆距为100 mm，船体梁第1 次变形挠度为31 mm；而试验工况3 中，相同工况条件下累积的变形挠度为44 mm，整体变形最大挠度相较于数值模拟结果大27.59%。说明前两次水下爆炸加载虽然没有造成船体梁的整体变形，但是中部发生了局部变形，使船体梁的总纵强度降低，从而使得试验中第3 次相同工况条件下船体梁的变形挠度更大。当爆距为100 mm、药量为1 g 时，3 次连续加载下船体梁的变形挠度为15 mm，而药量3 g 单次加载下船体梁的变形挠度为30 mm；当爆距为200 mm、药量为8 g 时，3 次连续加载下船体梁的变形挠度为25 mm，而药量24 g 单次加载下船体梁的变形挠度为48 mm。可以看出，在爆距相等的情况下，同等药量单次加载与均分药量3 次连续加载船体梁时，单次加载时船体梁的变形挠度大于均分多次加载。

4 结 论

(1) 数值模拟与试验结果具有较好的一致性，数值模拟方法可以研究多次水下爆炸对船体梁的累积毁伤规律。

(2) 当冲击因子Q较小时，多次水下爆炸对船体梁并未产生累积毁伤效应；当Q增大到一定值时，多次水下爆炸加载能够获得较好的累积效果，挠度与累积次数近似呈线性关系。

(3) 相同爆距下，同等当量炸药对船体梁进行单次和均分连续3 次水下爆炸加载作用下，其最终塑性变形挠度并不相同，均分3 次加载船体梁的变形挠度减小。