高维球冠上的Yamabe问题①
赖晋秋,胡玉琪,姚纯青
西南大学 数学与统计学院, 重庆 400715
文献[1]提出了Yamabe问题: 在每个m(≥3)维紧致无边黎曼流形(M,g)上, 是否存在一个与g共形且具有常数量曲率的度量? 经过文献[1-4]的研究, Yamabe问题得到了彻底的解决, 并由此带来几何分析中一系列新的进展[5].
长期以来, Yamabe问题的研究主要围绕着不带边界的紧致黎曼流形进行[6-7], 得到了令人满意的结果. 对于带非空边界的紧黎曼流形, 是否也有相应的Yamabe问题呢? 文献[8]研究了紧致带边流形上的Yamabe问题. 文献[9]通过构造局部测试函数, 给出了在带边流形上的Yamabe问题的一个存在定理. 文献[10-11]也讨论了具有正Ricc曲率和凸边界的紧黎曼流形的相关问题.
本文研究球冠上的Yamabe问题, 利用局部嵌入以及两次球极投影[12], 将标准球面上的度量诱导到球冠边界上, 得到球冠边界的度量[13]; 提出了球冠上的一类带边界条件的Yamabe方程, 并且得到了该方程的一组解.
1 预备知识

(1)
在球极投影下, 球面上的标准度量表示为
其中ξE是欧氏空间上的标准度量. 在欧氏空间Rn的笛卡尔坐标系下,ξE=δαβduα⊗duβ, 从而
(2)
(3)
球面的标准度量h是一个Einstein度量, 任何与h共形且具有常数量曲率的度量也是Einstein度量. 由于这个度量的Weyl曲率是0, 因此它具有常截面曲率. 所以这个度量与标准度量是等距的. 我们利用标准球面Sn上的球极投影, 以及Rn上的伸缩、 平移、 旋转变换, 构造出球面Sn上的共形变换, 从而得到以下结果:

(4)
该方程在λ=n(n-1)时具有标准解
(5)
其中β>1,x0是球面上的一点[14].
2 主要定理及其证明


图1 球冠及其边界上的球极投影
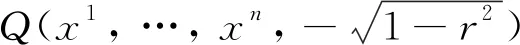
(6)
(7)
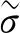

(8)
则
计算得到
(9)
由于g=φ*h, 所以
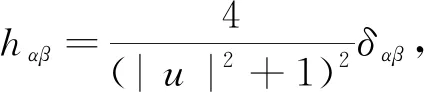
引理1得证.

(10)
这个方程在h是球面标准度量的情况下是有标准解的. 由引理1可知, 在给出h的共形度量下, 球冠边界也诱导出相应的共形度量
所以在边界(∂M,g)上, Yamabe方程为
(11)
定理1对于球冠M(n=dimM≥4), 带边界条件的Yamabe方程
(12)
证由球冠边界的度量, 我们很容易得到球冠边界(∂M,g)(n=dimM≥4)的数量曲率Sg. 由(1)式与引理1可知
令
从而可得
(13)
由(3)式得到球冠边界的数量曲率
(14)
我们知道, 标准球面Sn上的Yamabe方程具有标准解
其中β>1,x0是与球面上北极点相关的点,x是球面上任意一点. 那么这个解同样适用于球冠(Mn,h)上, 即满足
其中λ=n(n-1).
当这个共形变换只由伸缩、 旋转生成时, 易知x0为北极点N或南极点S, 此时φ0是旋转对称的. 当限制在球冠边界∂M上时,φ0为常数, 记为Λ, 从而
(15)

由(14)式可知
即在球冠边界∂M上, 满足
其中
我们将流形内部的几何性质与边界的几何性质相联系, 提出了球冠上的Yamabe方程的一类边界条件, 利用球面Yamabe方程的解, 构造出球冠上相应边值问题的解. 这样的结果能否推广到一般的带边界流形以及如何推广, 还有待进一步研究.

